Kein Folientitel
Werbung

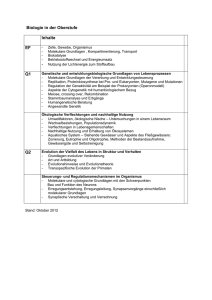
2.3 Molekulare Kräfte (in Flüssigkeiten) Flüssigkeit kondensierte Form der Materie molekulare Kräfte zwischen den mikroskopischen Teilchen (Atome, Moleküle) Größe solcher Kräfte: Kompressibilität k der Flüssigkeit inner-(intra-) molekulare Kräfte zwischen-(inter-) molekulare Kräfte DV k Dp V Unterschied Laplace-Gesetz Beispiel Wasser: k = 4·10-10 Pa-1 DV/V = 4·10-5 bei Druck von 105Pa=1 bar Flüssigkeiten sind elastisch hart! Zerreißfestigkeit einer Flüssigkeitssäule Kräfte zwischen zwei polierten Glasflächen als Modell für zwei benachbarte Flüssigkeitsschichten Kontakt Gewicht mit 10kg 100N Kohäsion Mikroskopische Betrachtung Kräfte auf ein Molekül durch die umgebenden Moleküle mittlere Schichtdicke Oberfläche Dx FR FR FR 0 Kohäsion intermolekulare Kräfte Arbeitsleistung zur Vergrößerung der Oberfläche Oberflächenspannung Spannen einer Oberfläche z.B. Lamelle DW J b F DA m 2 DW F Dx F Dx DA b b b F Dx Schwimmende Rasierklinge F b Wenn Vor- und Rückseite der Lamelle beachtet wird, ist dieser Ausdruck 2. Beispiel (H2O) = 7.3·10-2J/m2 Oberflächenspannung und Tropfenbildung Pipettenende Tropfen reißt ab, wenn: Schwerkraft > Kraft durch Oberflächenspannung d VT g d Tropfenform: Kugel, wenn frei schwebend VT g d Geometrie Hg Druck in der Kugel durch Oberflächenspannung: DV 12 r DA Volumenvergrößerung Hubarbeit: p·DV Oberflächenvergrößerung Oberflächenenergie: DA p DV DA p Material r 2 r Beispiel Wasser (20°C) = 7,3·10-2J/m2 r =1 mm Innendruck p =14,6 Pa = 0,1 mmHg ziemlich klein sehr kleiner Tropfen (Modell: ein Molekül umgeben von einer Schicht Moleküle) R 2Å = 2·10-10m p = 7,3·108 Pa 104bar, etwa eine Wassersäule von 100km molekularen Kräfte sind groß Schwerkraft des Tropfens nur 2Å Säule gegenüber Schwerkraft Adhäsion Zwischen-(inter-) molekulare Kräfte zwischen Grenzflächen unterschiedlicher Materialien Gleichgewicht zwischen Kohäsion und Adhäsion Form der Grenzflächen unvollkommen benetzend nicht benetzend benetzend Meniskus Adhäsion>>Kohäsion Wasser/Glas Adhäsion>Kohäsion Adhäsion<<Kohäsion Quecksilber Hg /Glas 0 180 Kapillarkräfte: Spezialfall von Kohäsion und Adhäsion biologische Systeme Hg/Glas Depression 2r h h 2 cos g r 2r H2O/Glas h Aszension Saugfähigkeit Zellstoff Adhäsion als Grenzflächenenergie Grenzfläche FR FR 0 Kohäsion > Adhäsion Statistische Verkleinerung der Gesamtoberfläche Hg-Tropfen 0 Sekunden 205 Tropfen Video 30 Sekunden 15 Tropfen 40 Sekunden 5 Tropfen 10 Sekunden 78 Tropfen 50 Sekunden 2 Tropfen 20 Sekunden 29 Tropfen 60 Sekunden 1 Tropfen Minimum der Oberflächenenergie