EinfidMet-II-1 - Meteorologisches Institut der Universität Bonn

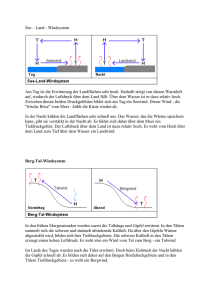
Einführung
in die Meteorologie
- Teil II: Meteorologische
Elemente Clemens Simmer
Meteorologisches Institut
Rheinische Friedrich-Wilhelms Universität Bonn
Sommersemester 2006
Wintersemester 2006/2007
Gliederung der Vorlesung
Allgemeines
I Einführung
II Meteorologische Elemente
III Thermodynamik der Atmosphäre
----------------------------------------------------IV Dynamik der Atmosphäre
V Synoptische Meteorologie
VI Allgemeine Zirkulation und Klima
II Meteorologische Elemente
II.1 Luftdruck und Luftdichte
II.2 Windgeschwindigkeit
II.3 Temperatur
II.4 Feuchte
II.5 Strahlung
II.1 Luftdruck und Luftdichte
• Zusammensetzung der Luft
• Ideale Gasgleichung + Daltonsches
Gesetz → Gasgleichung für die Luft
• Statische Grundgleichung
• Barometrische Höhenformel
• Druckmessung
• Globale horizontale Druckverteilung
II.1.1 Zusammensetzung der Erdatmosphäre
- Luft als ideales Gas • Die Luft besteht aus verschiedenartigen Luftmolekülen,
die sich in einem sonst massefreien Raum relativ
unabhängig voneinander (kaum Anziehungskräfte)
bewegen und i.w. nur durch Stöße miteinander
wechselwirken.
• In Luft ist das Volumen aller Moleküle zusammen (sog.
Eigenvolumen) sehr klein gegenüber dem Luftvolumen
selbst.
 Die Luft kann für meteorologische Belange als ein
ideales Gas, oder ein Gemisch von idealen Gasen
betrachtet werden.
II.1.1 Zusammensetzung der Erdatmosphäre
- Maßzahlen und Gesetz von Avogadro • 1 Mol mol: Maß für die Teilchenanzahl
– entspricht der Anzahl von 6,0228·1023 Teilchen (Loschmidtsche Zahl)
– entspricht der Anzahl der Atome in 12 g 12C-Atomen
• Molmasse M: Masse eines Mols (diese hängt vom Gewicht der
einzelnen Moleküle ab)
– M(C) =12 g/mol , M(O) =16 g/mol , M(O2)=32 g/mol
– M(O3)=48 g/mol , M(CO2)=44 g/mol , M(N2)=28 g/mol , M(H2O)=?
• Masse m: Masse einer beliebigen Stoffmenge in kg
• Molanzahl n: Anzahl der Mole in einer beliebigen Stoffmenge
angegeben in mol → M=m/n , n=m/M
• Molvolumen Vm: das Volumen, das ein Mol eines Stoffes einnimmt in
m3/mol (hängt von Druck und Temperatur des Gases ab)
• Gesetz von Avogadro:
 Ein Mol eines idealen Gases nimmt bei einer bestimmten
Temperatur und bestimmtem Druck immer das gleiche Volumen
ein.
 Beispiel: Bei T=273,15 K, p=1013,15 hPa, n=1 gilt V=0,02241 m3 (ca.
22 Liter) für jedes beliebige ideale Gas
II.1.1 Zusammensetzung der Erdatmosphäre
- die wichtigsten Gase (Volumen-% nach Graedel und Crutzen 1994) -
Bestandteil
Molmasse
Volumenoder
Mengen%
Massen%
Siedepunkt
in °C bei
1013 hPa
Stickstoff
N2
28,013
78,110
75,542
-193
Sauerstoff
O2
31,999
20,953
23,148
-183
Argon
Ar
39,948
0,934
1,288
-186
Kohlendioxyd
CO2
44,010
0,035
0,053
-78
Wasserdampf
H2O
18,01
0 - 10
0-5
100
Die nicht ganzzahligen Molmassen ergeben sich aus der Existenz von Isotopen.
Die Volumen-% des Teilgases ist der Volumenanteil, der sich ergibt, wenn man die Gase in
einem Volumen trennt, aber gewährleistet, dass in jedem Teilgas die gleiche Temperatur und
der gleiche Druck herrscht.
Der resultierende Volumenanteil ist dann auch das Verhältnis der Anzahlen der jeweiligen
Gaspartikel also der Molanzahlen (Mengen-%, Gesetz von Avogadro!).
Beim Siedepunkt ist der Dampfdruck des jeweiligen Gases gleich dem Gesamtluftdruck
(Bildung von Blasen in der Flüssigkeit gegen den Luftdruck). Bis auf Wasserdampf sind die
wichtigsten Gase bei atmosphärischen Verhältnissen nicht kondensiert vorhanden.
weiter …
•
•
•
•
Es gibt noch eine große Zahl von anderen wichtigen Gasen (siehe
folgende Tabelle) , u.a. Ozon (O3) und Lachgas (N2O). Doch ist ihr
Anteil sehr klein (Spurengase), obwohl ihre Bedeutung als
Strahlungsabsorber und –emitter (Treibhausgase) beträchtlich sein
kann.
Bis auf Wasserdampf und andere Gase mit ausgeprägten lokalen
Quellen und Senken sind alle Gase bis in ca. 80 km Höhe homogen
verteilt, d.h. Ihre Massen- und Volumenverhältnisse sind konstant. Bis
zu dieser Höhe dominiert die turbulente Durchmischung die
Sedimentation der Gase, welche sich durch ihre unterschiedliche
Schwere entmischen würden (siehe Weinkeller!, Zunahme der freien
Weglänge).
Wasserdampf ist meist in Bodennähe mit bis zu 5 % am stärksten
konzentriert. Die Ungleichverteilung trotz turbulenter Durchmischung
folgt daraus, dass sich die Wasserdampfquelle im/am Boden befindet
(Verdunstung von Wasser) und dass in der Höhe der Wasserdampf
durch Kondensation in Wolken Überschreitung der Sättigungsfeuchte)
und Ausregnen entnommen wird (Wasserkreislauf).
Eine weitere Besonderheit des Wasserdampfes im Vergleich zu den
anderen Gasen sein Vorhandensein in mehreren Phasen durch den
hohen Siedepunkt.
Einige troposphärische Spurengase
Bestandteil
Molmasse Volumen-%
Siedepunkt in °C
bei 1013 hPa
Neon
Ne
20,182
1,8·10-5
-246
Helium
He
4,003
5,2·10-4
-269
Methan
CH4
16,03
1-2·10-4
Krypton
Kr
83,8
1,0·10-4
-153
Wasserstoff
H2
2,016
5,0·10-5
-253
N 2O
44,016
2-6·10-5
-89
X
131,30
8,0 ·10-6
-107
CO
28,01
1-20 ·10-6
-191
48,000
1-3 ·10-6*
2-8 ·10-4**
-112
Lachgas
Xenon
Kohlenmonoxyd
Ozon
O3
außerdem kleine Anteile von CH2O, NO2, NH3, SO2, H2S, Cl2, J2, Rn,
1 ppmv= 10-6 =10-4 %, 1 ppbv= 10-9 =10-7 %, * bodennah, ** im stratosphärischen Maximum
Mittlere freie Weglänge der Moleküle
Höhe, km
Druck, hPa
Mittlere freie
Weglänge, m
Boden
1000
10-7
40
5
2·10-5
80
0,02
0,005
120
10-5
10
160
10-6
100
Die Turbulenz (nicht Diffusion) bestimmt die Vermischung der Gase in große
Höhen.
Ab ca. 100 km Höhe beginnt die mittlere freie Weglänge größer zu werden als
die Größe der Turbulenzelemente in der Luft – die Diffusion beginnt zu
dominieren.
Dann beginnen sich die einzelnen Moleküle unabhängig voneinander zu
bewegen und die Sedimentation beginnt.
Molmasse Ml des Gasgemisches Luft
Wir teilen in der Meteorologie die Luft in „trockene“ Luft und Wasserdampf ein.
Da die trockene Luft immer aus gleichen Gasanteilen zusammen gesetzt ist, ist
es praktisch eine gemittelte Molmasse für „trockene“ Luft zu bestimmen Ml.
Bezüglich dieser mittleren Molmasse gibt es dann auch eine hypothetische
Molzahl nl eines Gases mit Molmasse Ml.
Ml
M l  ml
ml

 Ml
   mi 
 i
 ml
mit ml Masse der Luft
mit mi Masse des Teilgases i und ml   mi
i

mi  M l 
1


  Mi
   M i ni 
M i  ml  i
 nl
 i
n
m
  M i i mit ni  i Mole des i - ten Teilgases
nl
Mi
i
m
und nl  l   ni Gesamtzahl der Mole
Ml
i
Vi
  Mi
, nach Avogadro , Vi , l Volumen des Teilgases bzw. Gesamtvolu men
Vl
i
 28,966 g/mol (ähnlich der des Stickstoff s)
Übungen zu II.1.1
1. Bestimme die Molmasse von Äthanol.
2. Bestimme aus dem Volumenanteil Vi/Vl eines Teilgases Vi am
Gesamtvolumen Vl seinen Massenanteil mi/ml in Abhängigkeit
vom Verhältnis der Molmassen. Verifiziere dies anhand der
Zahlen für den molekularen Sauerstoff in der Tabelle für die
Zusammensetzung der Erdatmosphäre.
3. Bestimme die Molmasse der Luft unter der Annahme, dass
diese zusätzlich zu den anderen Gasen in der ersten Tabelle
des Kapitels insgesamt drei (3) Volumen-% Wasserdampf
enthält. Die Volumenverhältnisse der „trockenen“ Gase
zueinander bleibe dabei unberührt. Was ergibt sich, wenn der
Wasserdampf 3% des Massenanteils ausmacht?
II.1.2 Gasgleichung für ideale Gase
- ideale Gasgleichung Druck (p), Temperatur (T) und Partikelanzahl (n= Anzahl der Mole des
idealen Gases im Volumen) sind verknüpft durch:
pV  nR*T
mit R*  8,3144 J/(mol K) allgemeine Gaskonstan te
m *
R*

R T  m T  mRM T
M
M
mit R  R* /M spezielle Gaskonstan te des Gases
Üblicherweise nutzen wir in der Meteorologie die Formulierung mit
der Dichte, da wir nicht von festen Luftvolumen ausgehen.
m R*
R*
p
T   T  RT
V M
M
Gasgleichung für ideale Gase
- ideale Gasgleichung pV  nR*T , p  RT
Wir postulieren hier nur die Gasgleichung. Wenn wir uns klar gemacht
haben werden, was Druck und Temperatur ist, werden wir erkennen, dass
wir die Gasgleichung nur benötigen, weil wir nicht individuelle Gasmoleküle
sondern sehr viele davon gemeinsam betrachten wollen.
Achtung: Die Gasgleichung ist eine diagnostische Gleichung, die drei
meteorologische Elemente verknüpft. Sie erklärt z.B. nicht, warum die
Temperatur in der Atmosphäre meist mit dem Druck abnimmt. Zur Erklärung
von Letzterem muss man nämlich Zusatzbedingungen festlegen (z.B. kein
Energie- und Massenaustausch).
Dichte, Volumen und Temperatur sind uns aus der unmittelbaren Erfahrung
bekannte Größen. Wir werden später lernen, dass die Temperatur propotional
zur mittleren kinetischen Energie der Luftmoleküle, und damit eng mit einer
Energieform – der Wärmeenergie – verbunden ist. Der Luftdruck ist uns nur
mittelbar vertraut; so wir wissen z.B. dass Druckunterschiede Bewegungen
auslösen.
Analyse von pV=nRT
V
p=const
V=const
T

 nR* 
 T
p  
 V const

1
p  nR T const
V
p
*
T=const
warm
kalt
p
V
 nR* 
 T
V  
 p const
V=const
T
V
p=const
T
Was ist Luftdruck?
• (Luft-)Druck ist Kraft/Fläche
• Luftdruck hat keine ausgezeichnete Richtung.
• Luftdruck wird spürbar z.B. durch die Impulsumkehr von
Luftmolekülen an einer Wand; ist der Impulsstrom gegen die
Wand auf der anderen Seite kleiner, so bewegt sich die Wand
dorthin
• Luftdruck ist die Flussdichte des Impulses der Luftmoleküle, was
die Einheitenanalyse aufdeckt:
Druck = Kraft / Fläche
= kg m/s2 / m2
= (kg m/s) / (m2 s)
= Impuls / (Fläche x Zeit)
• Diese Betrachtung gilt auch für jedes Teilgas einzeln, z.B. für
dem Dampfdruck des Wasserdampfes.
Warum erzeugen Luftdruckunterschiede (Gradienten)
Bewegung (1)?
Betrachte ein Volumen (blau) innerhalb einer Luftmasse (weiss).
Betrachte nun nur die Moleküle (rote und blaue Kugeln), die an beiden seitlichen
Enden des Luftvolumens in der Zeit Δt mit Umgebungsluftmasse ausgetauscht
werden.
t=to
t=to+Δt
Ist die Impulsflussdichte (=Druck) an beiden Enden gleich, d.h. gleichen sich die
Impulse der ausgetauschten Moleküle netto aus, so ändert sich der Gesamtimpuls
des Volumens nicht. Also keine Beschleunigung!
Warum erzeugen Luftdruckunterschiede
(Gradienten) Bewegung(2)?
Nun herrsche rechts ein höherer Druck als links durch höhere Temperatur
(=schnellere Bewegung=längere Pfeile)
t=to
t=to+Δt
Durch den Austausch hat das Volumen nun eine Gesamtimpulsänderung nach
links erfahren. Es wird also nach links beschleunigt!
Warum erzeugen Luftdruckunterschiede
(Gradienten) Bewegung(3)?
Wieder herrsche rechts ein höherer Druck, doch nun durch eine höhere Dichte
(=mehr Moleküle).
t=to
t=to+Δt
Wieder hat das Volumen hat eine Gesamtimpulsänderung nach links erfahren.
Es wird also wieder nach links beschleunigt.
II.1.3 Daltonsches Gesetz
- Gasgleichung für das Gasgemisch Luft •
•
•
Bei einem Gasgemisch ergibt sich der
Gesamtdruck aus den Partialdrücken der
einzelnen Gase (Daltonsches Gesetz).
Alle Komponentengase der Luft sind in
guter Näherung ideale Gase mit
speziellen Gaskonstanten Ri und durch
Impulsaustausch (Stöße) haben alle die
gleiche Temperatur.
Wasserdampffreie („trockene“) Luft hat
bis in große Höhen eine konstante
Gaszusammensetzung
→ RL=R*/ML=const
mit ML=28,965 g/mol
und RL=287 J/(kg K)
Nebenrechnung (siehe Übung II.1.1, 3b)
 ni
1
nL

 i
M L nL M L
mL
ni M i
i M
i


mL
pL   pi    i RiT
i
i
i
   L RiT
L
i

i R* 
T
  L  
 i L M i 
R*
 L
T   L RLT
ML
mi
i M
mi
i
i


mL
m
M
i
i l M i
L
i
Übungen zu II.1.2+1.3
1. Wasserdampffreie Luft habe den Druck 1000 hPa
und eine Dichte von 1 kg/m³. Welche Temperatur hat
sie?
2. In 5 km Höhe hat die Luftdichte auf die Hälfte des
Wertes am Boden (1000 hPa, 20°C) abgenommen.
Es herrsche eine Temperatur von – 30°C. Welcher
Luftdruck herrscht in 5 km Höhe?
3. Über kochendem Wassers bestehe die Luft
ausschließlich aus Wasserdampf. Welche Dichte hat
diese bei einem Luftdruck von 1013 hPa?
II.1.4 Statische Grundgleichung
und barometrische Höhenformel
- die statische Grundgleichung -1/ρ ∂p/∂z = g beschreibt
ein Gleichgewicht zwischen Schwerebeschleunigung
(Massenanziehung g) und der
Druckgradientbeschleunigung (-1/ρ ∂p/∂z)
- die barometrische Höhenformel ist die integrierte Form
der statischen Grundgleichung unter der Annahme,
dass der Druck nur von der Höhe abhängt
p(z)=-∫ρg dz + C
Ableitung der statischen
Grundgleichung ∂p/∂z=-ρg
- aus Skalenanalyse der 3. Komponente
der Bewegungsgleichung (nicht gezeigt)
- aus der 3. Komponente der
Bewegungsgleichung bei ruhender
Atmosphäre
- aus dem Gewichtsaspekt
Statische Grundgleichung aus
Bewegungsgleichung für ruhende
Atmosphäre

  

dv
1 
  p  g  2  v  FFr
dt


 v 0 
p
0
p
x
 0    x   0 
 


p
p
0
 0     y    0  
y
 0    p    g 
   z  

p
  g
z

1 
0   p  g

Achtung: Neben der
statischen Grundgleichung
fordert die ruhende
Atmosphäre auch
verschwindende
horizontale
Druckgradienten
Statische Grundgleichung aus
Gewichtsüberlegungen
Druck = Kraft/Fläche = Masse (m) x Beschleunigung (g) / Fläche (F)
pt=0
zt
z2
m‘
m, ρ, ΔV
p2
p1
p2 
m' g / F
p1  p2  p  mg / F  mg /( xy)
 p  Vg /( xy )  xyzg /( xy )
p
  g
z
z1
Δy
Δx
p1  mg / F  m' g / F
p p
lim

  g
z  0 z
z
Schwerebeschleunigung g ist nicht konstant!
• g beschreibt die integrale
Gravitationswirkung aller
Massen auf einen
Probekörper
• Durch die Abstands- (g
nimmt ab mit dem Abstand)
und Richtungsabhängigkeit
(g ist zur Masse hin
gerichtet) hängt g von der
Position des Probekörpers
zu den anderen Massen ab
• Beobachtung auf der Erde
(NN=Normalnull):

9,832 m/s 2 an den Polen

g  9,806 m/s 2 in 45 Breite
9,781 m/s 2 am Äquator



 auf NN


g
 0,031 ms -2 / 10 km
z

g ( , z )  9,80665 1  0,0026373 cos 2  0,0000059 cos 2 2 1  3,14 107 z
in m/s 2 mit  geographis che Breite und z Höhe über NN in m

Zur Breitenabhängigkeit der
Schwerebeschleunigung auf der Erde
Ellipsenform der Erde entstand als
Gleichgewichtsform zwischen
Newtonscher Gravitation und
Zentrifugalbeschleunigung.

gz

gN
 

g  g N  g Z mit

g N Newtonsche Anziehung (Graviatio n)

g Z Zentrifu galbeschle unigung

g muss senkrecht auf der Erdoberflä che sein

g
Barometrische Höhenformel
= Integration der statischen
Grundgleichung
über die Höhe z
p( z )
  ( z) g
z

p( z )  ?
Verschiedene Annahmen:
a) Homogene Atmosphäre (ρ(z)=const)
b) Isotherme Atmosphäre (T(z)=const)
c) Polytrope Atmosphäre (∂T/∂z=const)
Druckabnahme mit der Höhe in
der homogenen Atmosphäre
z
(z) = const, Dichte verändert sich mit der Höhe nicht.
Es gilt die statische Grundgleichung:
p
  g
z
z0
p
Der Druck hänge nur von der Höhe ab. Dann
dp
  g , dp   gdz
lassen sich die partiellen Änderungen (∂) in totale
dz
(d) umwandeln:
p( z)
z
z
Nach Variablentrennung (p↔z)
dp'   gd z '   g d z '
integriert man beide Seiten vom Boden
bis zur Höhe z (ρg=const):
p ( z  z0 )
z  z0
z0


p( z ' ) p ( z )  p( z )  p( z0 )   g z ' z   g ( z  z0 )
p( z)
Man erhält:

0
z
0
p( z )  p( z0 )  g ( z  z0 ) Der Druck p nimmt linear mit der
Höhe z ab; und zwar mit
ρg ~ 1,2x9,81 = 0,12 hPa/m
Druckabnahme in der isothermen
Atmosphäre (1)
z
T(z) = const, Temperatur ändert sich mit der Höhe nicht.
Dies ist eine bessere Näherung als ρ(z)=const.
Wie vorher können wir schreiben:
p
p
dp
  g ,
  g , dp   gdz
z
dz
Die Integration ist rechts nun nicht so einfach
möglich, da die Dichte ρ nun noch von der
Höhe z abhängt:
Die Gasgleichung gestattet
die Dichte ρ in die
Temperatur T umzurechnen,
die wir ja kennen
(T(z)=const). Dies ganz oben
eingesetzt ergibt:
z0
p( z)
z
p ( z  z0 )
z  z0
 dp'   g   ( z' )d z'
p  RLT ,   p
RLT
pg
1
g
dp  
dz ,
dp  
dz
RLT
p
RLT
Während rechts einfach zu integrieren ist, müssen wir für die linke Seite
noch die Stammfunktion von 1/p finden.
Die Stammfunktion von 1/p ist der natürliche Logarithmus ln p.
Druckabnahme in der isothermen
Atmosphäre (2)
T(z) = const, Temperatur ändert sich mit der Höhe nicht.
Dies ist eine bessere Näherung als ρ(z)=const.
z
z0
p
Dann erhalten wir für die Integration der linken Seite:
p( z)

p(z  z 0 )
1
p( z )
p( z)
dp'  ln p' p(z z )  ln p( z )  ln p ( z0 )  ln
0
p'
p ( z0 )
…und damit insgesamt:
p( z )
g
ln

p ( z0 )
RLT
Anwendung von exp(x) (=ex),
der Umkehrfunktion des ln
(ln(exp(x)≡exp(ln(x))=x)
…ergibt schließlich die
barometrische Höhenformel
für die isotherme
Atmosphäre:
z
 dz '  
z0
g
( z  z0 )
RLT


p( z )
g
 exp 

( z  z0 ) 


p ( z0 )
R
T
L




g
p( z )  p( z 0 ) exp 
  R T ( z  z0 ) 

L


Druckabnahme in der Atmosphäre
- Abhängigkeit von der Temperatur km
20
Annahme po=const
warm
mittel
kalt
10
isotherm
homogen
0
0
500
• Bei gleicher bodennaher
Temperatur ändert sich der
Druck in homogenen
Atmosphären in Bodennähe,
wie bei isothermen
Atmosphären der gleichen
Dichte am Boden (siehe
statische Grundgleichung).
• Warme Atmosphären
reichen höher oder haben in
größeren Höhen höhere
1000 hPa Drücke als kalte Atmosphären.
Druckabnahme in der
polytropen Atmosphäre (a)
Annahme: ∂T(z)/∂z = const
z
z0
p
T ( z )  T ( z0 )   ( z  z0 )
 g z

 g
 T ( z0 )   ( z  z0 )  
1



 
p( z )  po exp 
dz  p0 exp 
ln 


 RL z T ( z0 )   ( z  z0 ) 
R

T
(
z
)
L
0




0


 T ( z0 )   ( z  z0 ) 

p( z )  p0 
T ( z0 )


g
RL 
Übungen zu II.1.4
•
•
•
•
•
Wie hoch wäre unsere Atmosphäre (Bodendruck 1013,25 hPa,
Temperatur 15°C) unter Annahme einer mit der Höhe homogenen
Dichteverteilung?
Wie ändert sich die Temperatur in der homogenen Atmosphäre mit
der Höhe? Welche Temperatur herrscht dann an der
Atmosphärenobergrenze?
Welche Höhenänderung erfährt die 500 hPa-Fläche in einer
isothermen Atmosphäre von 0°C, wenn sich die Temperatur um ±1K
verändert?
Welchen Druck erfährt ein Pinguin im Vergleich zum Druck an der
Meeresoberfläche (der sei 1000 hPa), wenn er 10 m tief taucht?
Vernachlässige dabei die verschwindende Änderung der
Schwerebeschleunigung und der Dichte des Wassers mit der Tiefe.
Leite die barometrische Höhenformel für die polytrope Atmosphäre
ab.
II.1.5 Druckmessverfahren
• Flüssigkeitsbarometer
(Quecksilberbarometer)
– Prinzip: Waage
• Aneroidbarometer (Vidiedose)
– Prinzip: Kompressionsverformung
• Siedepunktbarometer (Hypsometer)
– Prinzip: Physik des Siedepunktes einer
Flüssigkeit
Flüssigkeitsbarometer
• Seit 1644 (Torricelli, Florenz, mit Quecksilber)
• 1654 (von Guericke, Magdeburg, mit Wasser)
• 1660: Erste Wettervorhersage mittels Barometer
Prinzip:
Vakuum
p
h
Kraft
mg
p

Fläche
q
hqg

 gh
q
Bestimme h, wenn die Flüssigkeit
Wasser ist und das Barometer am
Boden steht.
Stationsbarometer
Δl
h+Δh
h
q
Zweiter Schenkel ist zum
Gefäß erweitert
Q
q
h  l  l  l
Q
Barometerkorrektur
• Mit p = ρ g h = ρ(T) g(φ,z) h gibt es keine feste
Beziehung zwischen p und h.
• Skaleneinteilungen auf Barometern sind geeicht für
Standardwerte (i.a. z=0, Φ=45°, T=283,15.
• Lösung
 g
p  gh   0 g 0 h 
 bK
  0 g 0
Ablesung
b

Korrektur
K
c thermisch er Ausdehnung skoeffizie nt
 g
1
K


 f ( , z ) mit

 Temperatur in C
 0 g 0 1  c bekannt
aus
II.1.4
Für Quecksilber (Hg) gilt: ρ0 = 13595 kg/m³
c = 1,82·10-4 K-1
Aneroidbarometer
Vakuum
p
Prinzip:
Luftdruck drückt Dose teilweise zusammen
Idee:
Leipniz, 1702
Ausführung: Vidie, 1843 (Vidie-Dose)
Vorteile:
einfache Registrierung, transportabel
(z.B. Höhenmesser)
Nachteile: Hystereseeffekte, Reibungseffekte (Klopfen!),
regelmäßige Eichung notwendig
Siedepunktbarometer
• Wasser siedet, wenn sein Sättigungsdampfdruck
e* gleich dem Luftdruck p ist.
• Der Sättigungsdampfdruck (Partialdruck, bei dem
Wasserdampf kondensiert) ist nur eine Funktion
der Temperatur, also e* = e* (T).
• Misst man die Temperatur des Wasserdampfes
oberhalb siedenden Wassers, so kann man von T
auf e* (=p) schließen.
• Einfachste Ausführung:
Gasbrenner+Topf+Thermometer (bis 100°C!), z.B.
früher als Höhenmesser für Bergsteiger
Übungen zu 1.5
•
•
•
An einem Stationsbarometer in 50° geographischer Breite und in einer
Höhe von 100m über NN wird ein Druck von 990 hPa abgelesen. Die
Umgebungstemperatur des Quecksilberbarometers sei 10°C. Welcher
Druck herrscht wirklich?
Auf einem Berg der Höhe 2000 m herrsche tatsächlich ein Luftdruck
von 800 hPa und eine Temperatur von 0°C. Reduziere den Luftdruck
auf NN unter verschiedenen Annahmen (homogene, isotherme,
polytrope Atmosphäre mit T-Abnahme von 0,65 K/100m).
Warum siedet Wasser, wenn der Sättigungsdampfdruck über Wasser
gleich dem Luftdruck über der Wasseroberfläche ist?
II.1.6 Luftdruckverteilung und
Wind
• Der Luftdruck wird über den Gewichtsaspekt
durch das Gewicht der Luft darüber
beeinflusst.
• Variiert die Temperatur horizontal, so hat dies
also auch Auswirkungen auf die
Druckverteilung.
• Da Druckgradienten Luft beschleunigt,
bewirken Temperaturgradienten über
resultierende Druckgradienten Wind.
• Ein einfaches Beispiel hierfür ist die
thermisch direkte Zirkulation
Thermisch direkte Zirkulationen
• Bei gleichem Bodendruck wird sich die horizontale Druckverteilung in der
Höhe verändern, wenn es horizontale Temperaturunterschiede gibt. Liegt
z.B. warme Luft neben kalter Luft, so herrscht in der Höhe auf gleichen
Höhen in der kalten Luft ein niedrigerer Druck als in der warmen Luft.
• Der dann mit der Höhe zunehmende horizontale Druckgradient lässt dann
in der Höhe Luft von Warm (H) nach Kalt (T) fließen.
• Diese Massenumverteilung erhöht dann den Bodendruck in der Kaltluft
und erniedrigt ihn in der Warmluft; der entstehende Druckgradient am
Boden lässt dort dann Kaltluft (H) zur Warmluft (T) fließen. Eine
sogenannte thermisch direkte Zirkulation entsteht. Beispiele solcher
Zirkulationen sind der Land/Seewind und die Hadley-Zirkulation der
Tropen.
• Die Coriolisbeschleunigung lenkt die Strömung auf der Nordhalbkugel
nach rechts ab bis die Strömung parallel zu den Isobaren ist (sog.
geostrophischer Wind).
• Der geostrophische Wind ändert sich also mit der Höhe, wenn es
horizontale Temperaturgradienten gibt (sog. thermischer Wind).
Thermisch direkte Zirkulation
- mit geostrophischem und thermischem WindT
H
p-2Δp
p- Δp
p
W
T
T
K
H
K
2. Erwärmung links dehnt Druckflächen,
diese sind dann geneigt, es folgen
horizontale Druckgradienten und Luft setzt
sich zum tiefen Druck hin in Bewegung
1. keine horizontalen Temperaturgradienten, keine Luftbewegung
H
W
p-2Δp
p- Δp
p
p-2Δp
p- Δp
p
3. in der Höhe fließt Masse nach
rechts, sie erhöht dort überall den
Druck, während er rechts erniedrigt
wird, Druckunterschiede am Boden
und entsprechender Wind folgen
H
W
T
T
●
x
K
H
p-2Δp
p- Δp
p
4. Durch die Wirkung der
Coriolisbeschleunigung setzt in unteren
Schichten ein Wind in die Zeichenebene
hinein ein und in der Höhe aus der
Zeichenebene heraus.
Luftdruckverteilung am Boden
• folgt zunächst i.w. der Höhe der Erdoberfläche (100 m ↔ 10
hPa),
• Daher wird Bodendruck auf NN (Meereniveau) bezogen (=
Reduktion auf NN, nicht verwechseln mit Barometerkorrektur!);
Berechnung mit barometrischer Höhenformel unter Annahmen
über hypothetische Temperaturverteilung
• Beobachtete Extremwerte: 916 hPa im Islandtief, 1084 hPa im
asiatischen Kältehoch
• Übliche Spanne: 960-1040 hPa, Mittelwert 1013,25 hPa
Stationsmeldungen
Hochs und Tiefs
Fronten
Isobaren
27.10.2002 00 UTC
Bodenkarte enthält:
• Isobaren des reduzierten Luftdruckes im
Abstand von 5 hPa: reduziert heißt hypothetischer
Druck auf Meeresniveau (addiere ca. 1,2 hPa pro 10 m
Höhe über NN)
• Maxima und Minima des Bodendrucks:
Hoch (H)- und Tiefdruckgebiete (T oder L)
• Stationsmeldungen: Messungen von meist nur
einer Auswahl von Stationen, auf deren Basis die
Wetterkarte erstellt wurde
• Fronten: Luftmassengrenzen, die sich durch starke
horizonale Änderungen (Gradienten) in Temperatur
und/oder Feuchte und/oder Wind andeuten
Synoptische Wetterbeobachtungen
• weltweite Messungen an festen und bewegten (Schiffe)
Stationen zu „synoptischen“ Haupt-(0,6,12,18 UTC) und
Nebenterminen (3,9,15,21 UTC)
• Messungen:
–
–
–
–
–
–
Messungen von Druck, Temperatur und Feuchte in 2 m Höhe
Messung des Windes in 10 m Höhe
Niederschlagsmessung (Ablesung nur 6 und 18 UTC)
Maximum- (18 UTC) und Minimumtemperatur (6 UTC)
Wolkenbeobachtungen
allgemeine Wetterbeobachtungen
• sofortige Übermittlung der Messungen per Funk (früher
Fernschreiber) an Sammelstellen
synoptische Wetterbeobachtung
IIiii Nddff VVwwW PPPTT NLCLhCMCH TdTdapp 7RRTnTn 7RRTxTx
10111 81020 ccccc 12754 4cccc
55+06 7cc57
7cc51
6 UT
18 UTC
II
Zonenbezeichnung
iii
Stationskennung
N
Bedeckungsgrad
dd
Windrichtung in Dekagrad
ff
Windgeschwindigkeit in Knoten (1 kn =ca. 0,5 m/s)
VV
Sichtweite (kodiert)
ww
Wetter zum Beobachtungszeitpunkt
W
Wetter seit letztem Haupttermin (6 oder 3 Stunden)
PPP
Luftdruck ohne 100er, reduziert, in 10tel hPa
TT
Lufttemperatur in°C
NL
Bedeckungsgrad der tiefen Wolken
CL,M,H Art der tiefen, mittelhohe, hohen Wolken (kodiert)
h
Unterkantenhöhe der tiefsten Wolken (kodiert)
TD
Taupunkttemperatur in °C
a
Verlauf der Barographenkurve
pp
Luftdruckänderung in 10tel hPa der letzten 3 Stunden
RR
Niderschalg der vergangenen 12 Stunden (kodiert)
Tn,x
Minimum bzw. Maximumtemperatur
Aufbau des
Stationssymbols
TT
CH
PPP
VV
CM
pp
ww
N
TddTd h CL NL
a
W
Beispiel:
22°C Lufttemperatur, 18°C Taupunkt,
1021 hPa Luftdruck, um 0,5 hPa in
den letzten 3 Stunden gestiegen, 2/8
Bewölkung, nur niedrige Wolken,
Cumulus, Wind aus Ostsüdost mit 10
Knoten, die Sichtweite ist gering, es
gibt und ab keine signifikanten
Wettererscheinungen,…
Frontenkennzeichnung
Warmfront mit Erwärmung in allen Schichten
Warmfront mit Erwärmung nur am Boden
Warmfront mit Erwärmung nur in der Höhe
Maskierte Warmfront mit Abkühlung am Boden
Quasistationäre Front
Kaltfront mit Abkühlung in allen Schichten
Kaltfront mit Abkühlung nur am Boden
Kaltfront mit Abkühlung nur in der Höhe
Maskierte Kaltfront mit Erwärmung am Boden
Okklusionsfront (Zusammenschluß von Warm- und Kaltfront)
Gealterte Okklusionsfront
Warmfront-Okklusion mit Erwärmung am Boden
Kaltfront-Okklusion mit Abkühlung am Boden
Konvergenzlinie
27.10.2002 00 UTC
Zur Bodendruckkarte
1.
Winde sind parallel zu Isobaren mit niedrigem Druck links und
Richtungstendenz zum niedrigen Druck
2. Je enger die Isobaren, desto stärker der Wind
3. In Tiefs ist die Strömung links herum (zyklonal) in Hochs
rechts herum (antizyklonal)
4. 1-3 folgen aus der geostrophischen Windrelation (Ausgleich
von Druckgradient und Coriolisbeschleunigung, siehe auch
I.6)
5. Tiefs haben Frontalzonen (Warm- und Kaltfronten) an denen
die Isobaren (und der Wind) einen zyklonalen Sprung
aufweisen.
6. In Tiefs – besonders an Fronten – tritt vermehrt Bewölkung auf
(folgt u.a. aus Konvergenz der Luftströmung verbunden mit
Aufsteigen)
(→SLP-loop.ppt)
Klimatologische Verhältnisse
• langjährige Monatsmittel der Bodendruckverteilung (SLP, sea level
pressure) und des Windvektors (→SLP-JG-loop.avi).
• subtropische Hochdruckgürtel, hauptsächlich in den
Sommermonaten, Passatwindzonen hierdurch sehr irregulär.
• Dipolstruktur (Azorenhoch-Islandtief) über den Ozeanen der
Nordhemisphäre im Winter
• vorwiegend zonale (entlang den Breitenkreisen) Strömungen auf
der Südhemisphäre und starke meridionale Komponenten auf der
Nordhalbkugel
• Ausgedehntes (Hitze-)Tief über Asien im Sommer und
entsprechend ein (Kälte-)Hoch im Winter
• Schwache Tiefdruckrinne in den Tropen
• Monsune z.B. über Indien und Westafrika (jahreszeitliche lang
andauernde Windrichtungsänderung)
• Winde nicht mehr parallel zu Isobaren wegen nicht-linearem
Zusammenhang zwischen Druckfeld und Wind
Übungen zu II.1.6
•
•
Schätzen Sie anhand der Bodenwetterkarte durch Analyse von
mindestens drei Stationsmessungen den Zusammenhang zwischen
Stärke des Luftdruckgradienten und Windgeschwindigkeit ab. Die
Windgeschwindigkeit ergibt sich aus den Strichen am Ende des
Windpfeils (1/2 Strich=5 Knoten (kn), 1 kn = 0,514 m/s, 1 km/h = 0,278
m/s, also grob 1 m/s ~ 2 kn ~ 4 km/h). Vergleiche das Ergebnis mit der
geostrophischen Windrelation (siehe Skalenanalyse).
Zählen Sie wesentliche Unterschiede zwischen aktuellen
Bodenwetterkarten und mittleren Karten des Bodendruck- und
Windfeldes auf.