Vortrag über Explosives Brennen
Werbung

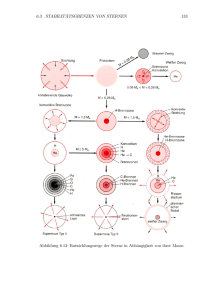
Explosives Brennen Von Katharina Büscher Inhalt: 1. Entwicklung massenreicher Sterne - Was sind massenreiche Sterne? - fortgeschrittene Brennstufen - Aufbau der „Zwiebelschalen“ 2. Supernovae Typ 2 - Kollaps des Eisenkerns - Schockwelle und Explosion - explosives Brennen 3. ...und danach? - tote Sterne, Überreste von Supernovaexplosionen 1. Entwicklung massenreicher Sterne Was sind massenreiche Sterne? → M > 8 M!! סּ → Durchlaufen aller Brennphasen → Supernova → relativ kurze Lebensdauer, in Regionen mit jungen Sternen, z.B. Spiralarme Beispiel: Progenitor der SN 1987a in der Magellanschen Wolke: 20 M סּ, Lebensdauer 107 Jahre Sonne: 1 Mסּ,, Lebensdauer 1010 Jahre Nukleare Brennphasen Wasserstoffbrennen Heliumbrennen Kohlenstoffbrennen Neonbrennen Sauerstoffbrennen Siliziumbrennen KOLLAPS 1. Wasserstoffbrennen Umwandlung H → He: p-p- Prozess , CNO- Zyklus pGravitation = ptherm. Verbrauch des Wasserstoffs pGravitation> ptherm. Kontraktion und Erwärmung (Virialtheorem: Ekin = 1/2 Epot) Zünden des Heliumbrennens; Aufblähen der Hülle; Wasserstoffschicht brennt weiter → ROTER RIESE 2. Heliumbrennen Umwandlung von He zu C im Kern über den tripel- α- Prozess: 4 He 4 He8 Be γ (E 0,1MeV ) Be 4He 12C (E 7,4MeV ) 8 Bildung von geringen Mengen O C 16O 12 (Resonanzen in der Nähe der He- Brennenergien) weiterhin H- Brennen in der Schale um dem He- Kern Tripel- alpha- Prozess Übergang zwischen den hydrostatischen Brennphasen Verbrauch des Brennstoffes Überhandnehmen des Gravitationsdruckes Kontraktion Erwärmung, Druckanstieg Zündung der nächsten Brennphase Expansion 3. C -, Ne -, O - Brennen Coulombbarriere bei C am niedrigsten → Kohlenstoffbrennen zuerst: C 12C 20Ne 12 C 12C 23Na p 12 C 12C 23Mg n 12 Ne- Brennen: 20 Ne 4He24Mg 20 Ne 4He 16O Wie? → Photodesintegration! O- Brennen: Synthese von S, P, Mg, Si Gegen Ende des O- Brennens: T9 = 2 4. Siliziumbrennen Temperatur nicht groß genug für Si + Si → X → Photodesintegration: T9 = 3: Zerstörung von Kernen durch (,p) (,n) (,α) p / n / α + unzerstörter Kern → stabilerer Kern + 28 Si 32S 32 S 36Ar ... 52 Fe 56Ni EBindung pro Nukleon maximal für Fe → Sukzessive Bildung von Fe e p n e Schwache WW, z.B. Elektroneneinfang → Kühlung durch Neutrinos → schnelleres Brennen e n p e Lebenslauf eines Sterns mit 25 Mסּ Elementverteilung im Universum: (log. Skala!!): „ Zwiebelschalenmodell“ 2) Supernova vom Typ 2 Stabilität des Fe- Kerns Stern vor Kollaps: M = 15M סּMKern = 1,5 M סּT9 =8 ρ = 3,7*109 g/cm³ kein Brennen im Kern → Warum kein sofortiger Kollaps? Gegendruck der Elektronen: prel. 1 4/3 (3 ²)1/ 3 ne 4 Unschärferelation + Pauli-Prinzip + großes ρ → Entartung p durch EFermi bestimmt → abhängig von Elektronendichte ne vorheriger Mechanismus funktioniert nicht mehr Kollaps des Kerns MKern > MChand → pGravit > pel Beschleunigung des Kollaps: M Chand 1,4 mp 1,5 M Sonne 3/ 2 1) Photodesintegration von Fe verringert ptherm der Elektronen 56 Fe 13He 124,4MeV 2) Elektroneneinfang an p und leichten Kernen → ne kleiner → pel kleiner e p n e e ZAX Z A1 X e 3) Kühlung durch entweichende Neutrinos → sehr schnelle Kontraktion innerhalb von Sekundenbruchteilen → Entkoppeln der Entwicklung des Kerns von der Hülle Kollaps des Kerns Geschwindigkeitsverteilung der einfallenden Materie: vr Innere Hälfte kollabiert homolog Materie außerhalb des Schallpunktes mit v = vSchall kollabiert mit für den freien Fall charakteristischen Geschwindigkeiten Kollaps des Kerns Neutrino- Trapping ρ = 1011 g/cm³: λNeutrino < rKern → Neutrinos „gefangen“, Bewegung mit einfallender Materie → Kollaps adiabatisch da keine Kühlung, S konstant ρ = 1012 g/cm³: Einstellen des Gleichgewichtes bzgl. der schwachen WW ne konstant p e n Keine weitere Veränderung der Zusammensetzung Kontrahierendes Gas aus Elektronen, Neutronen, Neutrinos und Kernen Rückstoß und Druckwelle ρ0 = 2,7 * 1014 g/cm³ Auflösung der Kernstrukturen → „Riesenkern“ Keine weitere Kontraktion möglich Rückstoß (steife Feder) Materie schwingt zurück Zusammenstoß mit einfallender Materie Schockwelle Schockwelle Schockwelle dissoziiert Fe- Kerne Verlust von Energie → Abschwächung Druckanstieg → Beschleunigung der einfallenden Materie über Fluchtgeschwindigkeit EXPLOSION Neutrino- Heizung Fe- Dissoziation → λNeutrino wieder größer → Neutrinos sammeln sich hinter Schockwelle Falls Schock genug Energie → Ausbreitung bis zu Gebieten mit ρ < 1011 g/cm³ Plötzliches Freiwerden der Neutrinos „Anheizen des Schocks“ Was bisher geschah: 1. • 2. • • • • 3. • • • • Durchlaufen aller Brennphasen: H, He, C, Ne, O, Si, Elementsynthese bis Fe Kollaps des Kerns: Überwinden des pel Beschleunigung durch Photodesintegration, Elektroneneinfang, Neutrinokühlung Neutrino- trapping, Übergang zum adiabatischen Kollaps Rückstoß bei nuklearer Dichte Schockwelle: Abschwächung der Schockwelle im Fe- Kern Heizen der Schockwelle durch Neutrinos Supernovaexplosion durch Beschleunigen der Materie Gravitationsenergie → Ekin, Eem (1%) und (99%) Explosives Brennen Schockwelle läuft durch die verschiedenen Schichten der Hülle → Energieabgabe an Materie in den Schalen, Temperaturerhöhung Modell: strahlende Blase, die die meiste Energie enthält → 500 keV in Siliziumschicht → 100 keV in O- Ne- Schicht → 10 keV in H- Schicht TS (3E0 / 4 a r0 ³ 1/ 4 → Zünden in Ne-, O-, und Si- Schicht für einige Zehntelsekunden → Nachträgliche Modifikation der Elementhäufigkeit ...und danach? Hülle: Materie wird in den interstellaren Raum geschleudert → Bildung neuer Sterne, Planeten... z.B. unsere Sonne Restkern: Je nach Masse 1. Neutronenstern (MKern < 8M)סּ • Bildung entarteter Neutronen • p e n e Freigesetzte Energie: Differenz der Bindungsenergie ΔE ≈ 1053 ergs 3 1 1 E pot GM 0 ² 5 R R0 Bsp.: R = 10 km, M0 = 2M → סּΔM/M0 = 0,2 M 3 M G 0 M0 5 Rc ² Schwarzes Loch (MKern > 8M)סּ 2. • Zusammenziehen der Masse auf Singularität • Schwarzschild- Radius R = 2GM/c² ENDE