Vorlesung 0 Sterne und ISM
Werbung

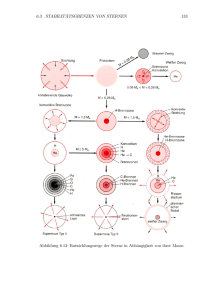
Sterbende Sterne und das interstellare Medium Das große Ganze zu Beginn Der Materiekreislauf Das interstellare Medium 1. Entwicklung massenreicher Sterne Was sind massenreiche Sterne? → M > 8 M!! סּ → Durchlaufen aller Brennphasen → Supernova → relativ kurze Lebensdauer, in Regionen mit jungen Sternen, z.B. Spiralarme Beispiel: Progenitor der SN 1987a in der Magellanschen Wolke: 20 M סּ, Lebensdauer 107 Jahre Sonne: 1 Mסּ,, Lebensdauer 1010 Jahre Nukleare Brennphasen Wasserstoffbrennen Heliumbrennen Kohlenstoffbrennen Neonbrennen Sauerstoffbrennen Siliziumbrennen KOLLAPS Wie erhält man die Leuchtkraft eines Sterns? Zur Berechnung der Leuchtkraft L benötigt man: Scheinbare Helligkeit (S) Entfernung zum Stern (R) Denn: L 4R S 2 W S 2 m Scheinbare Helligkeit Wird durch Energie des einfallenden Lichts definiert Mit Hilfe eines Photometers kann die Strahlungsleistung pro Quadratmeter ermittelt werden Einführung einer relativen Skala mit Stern Wega als Referenz Einheit der scheinbaren Helligkeit m: Magnitude (mag) Scheinbare Helligkeit ist definiert durch: S m 2,5 lg 10 W ega S J S m² s Beispiele: Sonne m = -26,8 mag, Sirius m = -1,5 mag Entfernungsbestimmung Aus einer Winkelmessung – Parallaxe p 1' ' ˆ 3,26Lj 1pc Bis zu einer Entfernung von 1000pc möglich Aus pulsationsveränderlichen Sternen – Cepheiden Grössenänderung → Helligkeitsänderung Tatsächliche Helligkeit proportional zu Pulsationsperiode Vergleich mit scheinbarer Helligkeit liefert Entfernung Grundgleichungen der stabilen Sterne Warum treten die Zustandsgrößen Leuchtkraft, Temperatur, Radius, Masse, Helligkeit und Spektraltyp nur in bestimmten Kombinationen auf? Gleichgewichtsbedingungen: Hydrostatisches und thermisches Gleichgewicht Massenverteilung und Energietransport Hydrostatisches Gleichgewicht “Kampf“ gegen die Gravitation Entgegengesetzte Kraft muss Kollaps verhindern → Druck dP Mr G 2 dr r Thermisches Gleichgewicht Energiefluss durch Sternoberfläche in Form von Strahlung (Leuchtkraft) Energieerhaltung: Energieverlust an der Sternoberfläche muss gleich der Energieerzeugung im Sterninnern sein R L (r ) (r )4r ² dr 0 dL(r ) (r ) (r )4r ² dr J g s kg 3 m Massenverteilung Beziehung zwischen Masse, Radius und Dichte eines Sterns Gibt an, wie sich die Masse mit dem Abstand zum Sternenzentrum ändert dV 4r ² dr dM r (4r ² dr ) dM r 4r ² dr Energietransport 3 Transportmechanismen Strahlung: Photonenabsorption und -emission Konvektion: Materialaustausch Wärmeleitung: Teilchenkollision dT 3 Lr dr 4ac T ³ 4r ² T: Temperatur : Rosseland Opazität (Absorptionskoeffizient) a: Stefan-Boltzmann Konstante Energiequellen der Sterne Leuchtkraft: L 3,85 10 W Steinkohle: Brenndauer ungefähr 10000 Jahre Gravitationspotential: 2 26 M EG E pot ( R) G R HK Kernfusion: 1 EG 7 3 10 Jahre 2 L E N 0,008 Mc 2 EN N 1011 Jahre L Kernfusion Verschmelzung zweier Atomkerne Überwindung des Coulomb-Potentials durch Tunneleffekt Reaktionsrate ~ Maxwell-Boltzmann-Verteilung * Tunnelwahrscheinlichkeit pp-Reaktion Massendefekt / Bindungsenergie Massendefekt: Masse eines Atomkerns ist stets kleiner, als die Summe der Massen von N Neutronen und Z Protonen Energie bleibt durch Einsteins Masse-EnergieÄquivalenz E=mc² erhalten Bindungsenergie: B(Z , N ) Zmp Nmn m(Z , N ) c 2 Maximum der Bindungsenergie pro Nukleon liegt im Periodensystem bei Eisen Bethe-Weizsäcker-Formel B 2 3 av A Volumenterm ac Z 2 A as A Oberflächenterm 2 CoulombTerm A 1 aA Z A a p A 2 1 2 Paarungsterm Asymmetrieterm R~ A 1 3 1 3 R: Kernradius A: Nukleonenzahl PP-Kette 4 H He 2e 2 e 2 26,2MeV 1 1 4 2 Startreaktionen: p p H e e 1,19MeV 2 1 2 1 H p He 5,49MeV 3 2 p n e e (alle 1010 Jahre) Hauptfolgereaktionen 3 Reaktionsketten PP-Reaktion I: PP-Reaktion II: 3 2 3 2 He He He 2 p 12,89MeV 3 2 4 2 7 4 Be e Li e 7 3 PP-Reaktion III: 4 2 He He Be 1,59MeV 7 4 3 2 7 3 Li p 2 He 17,35MeV 4 2 He 24He 47 Be 1,59MeV 7 4 Be p58B 0,14MeV 8 5 8 4 B Be e e 8 4 Be 2 24He CNO-Zyklus Kohlenstoff, Stickstoff und Sauerstoff dienen als Katalysator für Wasserstoffbrennen Sternentwicklung Nützliche Beziehungen, die sich aus Grundgleichungen ergeben: Masse-Leuchtkraft-Beziehung L~M 72 Massereiche Sterne strahlen mehr Energie ab (sind heller) Temperatur-Masse-Beziehung M T ~ M 23 Massereiche Sterne sind heißer Lebensdauer-Masse-Beziehung t Hauptreihe 10 10 M M 52 Massereiche Sterne leben kürzer Höhere Temperatur größere Leuchtkraft größer Masse kürzere Lebensdauer Sternentstehung Gaswolke, die aufgrund ihrer eigenen Schwerkraft kollabiert, erreicht Bedingungen, um Wasserstoffbrennen zu zünden Kontraktion Dichte freiwerdende Gravitationsenergie Temperatur Wasserstoffbrennen findet nur im Sternenzentrum statt (wg. Bedingungen) Sind ca. 10% des Wasserstoffs verbrannt, ist Wasserstoffbrennphase beendet Objekte unter 0,07 Sonnenmassen erreichen nicht die nötige Temperatur, um Kernfusion zu zünden Was passiert nach dem Wasserstoffbrennen? Weitere Entwicklung ist massenabhängig Stern kontrahiert Energiegewinnung durch Gravitationspotential Bedingungen für Heliumbrennen erfüllt ( Stern verlässt Hauptreihe Roter Riese) Bei massereichen Sternen kann nach Heliumbrennen Kohlenstoff- bis Siliziumbrennen einsetzen Spätphasen der Sternentwicklung Durch Temperatur und Leistungsanstieg expandiert der Stern zu einem roten Riesen Äußere Hülle wird abgestoßen (Planetarischer Nebel); Masse des Restkerns entscheidet über Endstadium < 1,4 Sonnenmassen Weißer Zwerg > 1,4 Sonnenmassen Supernova Restkern < 3 Sonnenmassen Neutronenstern Restkern > 3 Sonnenmassen Schwarzes Loch Wasserstoffbrennen Umwandlung H → He: p-p- Prozess , CNO- Zyklus pGravitation = ptherm. Verbrauch des Wasserstoffs pGravitation> ptherm. Kontraktion und Erwärmung (Virialtheorem: Ekin = 1/2 Epot) Zünden des Heliumbrennens; Aufblähen der Hülle; Wasserstoffschicht brennt weiter → ROTER RIESE Heliumbrennen Umwandlung von He zu C im Kern über den tripel- α- Prozess: 4 He 4 He8 Be γ (E 0,1MeV ) Be 4He 12C (E 7,4MeV ) 8 Bildung von geringen Mengen O C 16O 12 (Resonanzen in der Nähe der He- Brennenergien) weiterhin H- Brennen in der Schale um dem He- Kern Tripel- alpha- Prozess Übergang zwischen den hydrostatischen Brennphasen Verbrauch des Brennstoffes Überhandnehmen des Gravitationsdruckes Kontraktion Erwärmung, Druckanstieg Zündung der nächsten Brennphase Expansion 3. C -, Ne -, O - Brennen Coulombbarriere bei C am niedrigsten → Kohlenstoffbrennen zuerst: C 12C 20Ne 12 C 12C 23Na p 12 C 12C 23Mg n 12 Ne- Brennen: 20 Ne 4He24Mg 20 Ne 4He 16O Wie? → Photodesintegration! O- Brennen: Synthese von S, P, Mg, Si Gegen Ende des O- Brennens: T9 = 2 4. Siliziumbrennen Temperatur nicht groß genug für Si + Si → X → Photodesintegration: T9 = 3: Zerstörung von Kernen durch (,p) (,n) (,α) p / n / α + unzerstörter Kern → stabilerer Kern + 28 Si 32S 32 S 36Ar ... 52 Fe 56Ni EBindung pro Nukleon maximal für Fe → Sukzessive Bildung von Fe e p n e Schwache WW, z.B. Elektroneneinfang → Kühlung durch Neutrinos → schnelleres Brennen e n p e Lebenslauf eines Sterns mit 25 Mסּ Elementverteilung im Universum: (log. Skala!!): „ Zwiebelschalenmodell“ 2) Supernova vom Typ 2 Stabilität des Fe- Kerns Stern vor Kollaps: M = 15M סּMKern = 1,5 M סּT9 =8 ρ = 3,7*109 g/cm³ kein Brennen im Kern → Warum kein sofortiger Kollaps? Gegendruck der Elektronen: prel. 1 4/3 (3 ²)1/ 3 ne 4 Unschärferelation + Pauli-Prinzip + großes ρ → Entartung p durch EFermi bestimmt → abhängig von Elektronendichte ne vorheriger Mechanismus funktioniert nicht mehr Kollaps des Kerns MKern > MChand → pGravit > pel Beschleunigung des Kollaps: M Chand 1,4 mp 1,5 M Sonne 3/ 2 1) Photodesintegration von Fe verringert ptherm der Elektronen 56 Fe 13He 124,4MeV 2) Elektroneneinfang an p und leichten Kernen → ne kleiner → pel kleiner e p n e e ZAX Z A1 X e 3) Kühlung durch entweichende Neutrinos → sehr schnelle Kontraktion innerhalb von Sekundenbruchteilen → Entkoppeln der Entwicklung des Kerns von der Hülle Kollaps des Kerns Geschwindigkeitsverteilung der einfallenden Materie: vr Innere Hälfte kollabiert homolog Materie außerhalb des Schallpunktes mit v = vSchall kollabiert mit für den freien Fall charakteristischen Geschwindigkeiten Kollaps des Kerns Neutrino- Trapping ρ = 1011 g/cm³: λNeutrino < rKern → Neutrinos „gefangen“, Bewegung mit einfallender Materie → Kollaps adiabatisch da keine Kühlung, S konstant ρ = 1012 g/cm³: Einstellen des Gleichgewichtes bzgl. der schwachen WW ne konstant p e n Keine weitere Veränderung der Zusammensetzung Kontrahierendes Gas aus Elektronen, Neutronen, Neutrinos und Kernen Rückstoß und Druckwelle ρ0 = 2,7 * 1014 g/cm³ Auflösung der Kernstrukturen → „Riesenkern“ Keine weitere Kontraktion möglich Rückstoß (steife Feder) Materie schwingt zurück Zusammenstoß mit einfallender Materie Schockwelle Schockwelle Schockwelle dissoziiert Fe- Kerne Verlust von Energie → Abschwächung Druckanstieg → Beschleunigung der einfallenden Materie über Fluchtgeschwindigkeit EXPLOSION Neutrino- Heizung Fe- Dissoziation → λNeutrino wieder größer → Neutrinos sammeln sich hinter Schockwelle Falls Schock genug Energie → Ausbreitung bis zu Gebieten mit ρ < 1011 g/cm³ Plötzliches Freiwerden der Neutrinos „Anheizen des Schocks“ Was bisher geschah: 1. • 2. • • • • 3. • • • • Durchlaufen aller Brennphasen: H, He, C, Ne, O, Si, Elementsynthese bis Fe Kollaps des Kerns: Überwinden des pel Beschleunigung durch Photodesintegration, Elektroneneinfang, Neutrinokühlung Neutrino- trapping, Übergang zum adiabatischen Kollaps Rückstoß bei nuklearer Dichte Schockwelle: Abschwächung der Schockwelle im Fe- Kern Heizen der Schockwelle durch Neutrinos Supernovaexplosion durch Beschleunigen der Materie Gravitationsenergie → Ekin, Eem (1%) und (99%) Explosives Brennen Schockwelle läuft durch die verschiedenen Schichten der Hülle → Energieabgabe an Materie in den Schalen, Temperaturerhöhung Modell: strahlende Blase, die die meiste Energie enthält → 500 keV in Siliziumschicht → 100 keV in O- Ne- Schicht → 10 keV in H- Schicht TS (3E0 / 4 a r0 ³ 1/ 4 → Zünden in Ne-, O-, und Si- Schicht für einige Zehntelsekunden → Nachträgliche Modifikation der Elementhäufigkeit ...und danach? Hülle: Materie wird in den interstellaren Raum geschleudert → Bildung neuer Sterne, Planeten... z.B. unsere Sonne Restkern: Je nach Masse 1. Neutronenstern (MKern < 8M)סּ • Bildung entarteter Neutronen • p e n e Freigesetzte Energie: Differenz der Bindungsenergie ΔE ≈ 1053 ergs 3 1 1 E pot GM 0 ² 5 R R0 Bsp.: R = 10 km, M0 = 2M → סּΔM/M0 = 0,2 M 3 M G 0 M0 5 Rc ² Schwarzes Loch (MKern > 8M)סּ 2. • Zusammenziehen der Masse auf Singularität • Schwarzschild- Radius R = 2GM/c² Überrest Von der Milchstraße zum Virgo-Galaxienhaufen M51 – eine Spiralgalaxie Sterne und Staubwolken Entstehung der Sterne heiße O-, B-Sterne junger Stern verhüllte Protosterne Dunkelwolke Dunkelwolke HST 2004 Der Orion-Nebel Sterne im Werden Aus einer Wolke werden Sterne Zuerst, etwas einfaches: Sterne Druck balanziert Schwerkraft Die Sonne Massendefekt Bei der Fusion zweier Teilchen zu einem dritten wird Bindungsenergie in Form von Strahlung frei E m c 2 Wasserstoffbrennen in der Sonne Massendefekt bei Kernfusionsprozessen beträgt weniger als 1% der Masse der Ausgangskerne Unsere Sonne Neutrinos brauchen nur 2 sec vom Inneren an die Oberfläche! Neutrinos aus der Sonne Kernfusion in der Sonne: 4p 4He + 2e+ + 2e + 27 MeV Energie auf der Erde: 1011 solare Neutrinos / cm2 und Sekunde Produktion: 100% als „e-Pendel“ e ? ? Davis (1970 -2000): e Nachweis auf der Erde Ergebnis: nur 30% der erwarteten e Bestätigung (1995) Kamiokande (Sonne live! im „Neutrinolicht“) Energiehaushalt Verbrauchte Energie Freigesetzte Energie H He C Fe Nukleosynthese Entwicklungszeiten für einen 15 M Stern Verschm . Produkt H 4He 107 Jahre 4He 12C einige 106 Jahre 1 108 K 16O, 20Ne, 12C 20Ne 24Mg, 4He + 16O 28Si + 56Fe 16O, 24Mg 28Si, 32S 56Fe Neutronen Zeit Temperatur 4 106 K 1000 Jahre 6 108 K wenige Jahre 109 K Ein jahr 2 109 K Tage 3 109 K < eine Sekunde > 3 109 K Supernova-Überrest CXO in Casseopeia A Elementspedition Supernova – Just in Time … Kosmischer Kreislauf