Externe Datenstruktur lineare geordnete Liste

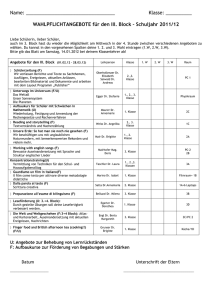
Externe Datenstruktur
lineare Liste
Agenda




Das Externspeichermodell
Lineare geordnete Listen
Eine „naive“ Implementierung
Eine „bessere“ Implementierung
◦ Aufbau
◦ Operationen


Optimierungsmöglichkeiten
Quellen
16.05.2016
2 /13
Das Externspeichermodell
B1
CPU
Hauptspeicher,
Main Memory
B2
Bn
Externspeicher
1 I/O
16.05.2016
3 /13
Lineare geordnete Listen
aufsteigend sortiert
Array
Operationen:
Anfang
einfach
verlinkte Liste
2
5
11
50
99
27
55
78
89
Anfang
doppel
verlinkte Liste
26
Anfang
- Search (x)
Suchen eines Elementes innerhalb
der Liste mit dem Schlüssel ‚x‘
- Insert (x)
Fügt ein Element mit dem
Schlüssel ‚x‘ in die Liste
- Delete (x)
Entfernt ein Element mit dem
Schlüssel ‚x‘ aus die Liste
Ende
16.05.2016
4 /13
„Naive“ Implementierung 1/2
Search(x):
Es wird über jedes Element in den Blöcken der Liste traversiert, auf der Suche
nach dem Element mit dem Schlüssel ‚x‘.
ges. N/B I/Os
Insert(x):
Jeder Block wird einzeln durchlaufen, auf der Suche nach einem der Ordnung
entsprechenden Platz.
N/B I/Os
Falls der passende Block einen verfügbaren Platz besitzt, so wird das Element
mit dem Schlüssel ‚x‘ eingefügt.
1 I/O
Falls der passende Block keinen verfügbaren Platz hat, so wird dieser in zwei
Blöcke zu je B/2 Elemente aufgespalten. Beide Blöcke werden anschließend
zurückgeschrieben.
2 I/O
ges. N/B+3 I/Os
16.05.2016
5 /13
„Naive“ Implementierung 2/2
Delete(x):
Es wird über jedes Element in den Blöcken der Liste traversiert, auf der Suche
nach dem Element mit dem Schlüssel ‚x‘ (Search(x)).
N/B I/Os
Das gesuchte Element wird aus dem Block entfernt und der betreffende Block
wird zurückgeschrieben.
1 I/O
ges. N/B+1 I/Os
Die „naive“ Implementierung lässt sich optimieren…
16.05.2016
6 /13
„Bessere“ Implementierung - Aufbau 1/2
Indexarray:
interner Speicher
Beinhaltet Schlüssel des ersten Elements jedes Blocks
(Key x), den dazugehörigen Zeiger dieses Blocks im
externen Speicher (ptr y) und die Anzahl der
Elemente innerhalb des Blocks (n).
Länge des Arrays: N/B
Key 1
ptr 1
B1
5
……
……
Key x
ptr y
3
Bn
Blockarray:
Ein Block wird repräsentiert als Array der Länge: B
16.05.2016
7 /13
„Bessere“ Implementierung - Aufbau 2/2
Blockplätze:
interner Speicher
Zum Mischen und Aufspalten der Blöcke bei Bedarf.
Entspricht der Größe von: 2B
Optimierungsziel:
Zu jeder Zeit sollten sich in einem Paar aufeinander
folgender Blöcke 2/3 B an zusammengehörigen
Elementen befinden.
(Minimierung der Blockanzahl)
Beispiel Blockgröße: B = 5
|Bx| = #Elemente
B1
|B2| + |B3| > 2/3 B
B2
B3
…
Bn
|B1| + |B2| > 2/3 B
16.05.2016
8 /13
„Bessere“ Implementierung – Operationen 1/3
Search(x):
- Führe binäre Suche auf dem Indexarray durch. Da alle ersten Schlüssel im
Indexarray gespeichert sind, kann der gesuchte Block anhand der Schlüssel
seiner Nachbarblöcke gefunden werden.
- Führe eine binäre Suche auf das Blockarray durch.
1 I/O
Search(5)
ges. 1 I/O
1
ptr B1
B1
1
2
3
7
ptr B2
1
8
3
ptr B3
B2
5
7
B3
8
10
13
Search(5)
16.05.2016
9 /13
„Bessere“ Implementierung – Operationen 2/3
Insert(x):
Passender Block kann für das Einfügen analog zur Search(x)-Operation
gesucht werden.
1 I/O
Fall 1 – Gesuchter Block bietet Platz zum Einfügen
Füge das Element ein und verschiebe wenn nötig die nachfolgenden Elemente
dieses Blockes. *
2 I/Os
Fall 2 – Gesuchter Block bietet keinen Platz zum Einfügen
a) Falls ein benachbarter Block noch eine Einfügemöglichkeit besitzt, so füge
Element in diesen ein bzw. tausche Elemente aus. (Minimierung #Blöcke) *
b) Neuer Block wird mit der Hälfte der Elemente des vollen Blocks erzeugt.
Element wird nun in den richtigen Block eingefügt. *
3 I/Os
Bx
Bx+1
1
Bx+2
2
Beispiel Blockgröße: B = 3
5
7
9
ges. max. 4 I/Os
Bx+3
13
15
17
19
4
* ggf. Indexarray aktualisieren
16.05.2016
10 /13
„Bessere“ Implementierung – Operationen 3/3
Delete(x):
Element mit Schlüssel ‚x‘ kann analog zur Search(x)-Operation gesucht
werden. Element kann nun entfernt werden. *
1 I/O
Fall – Block (Bx) hat nun < B/3 Elemente
Prüfe ob ein Nachbarblock in der Summe mit Block Bx höchstens 2/3 Elemente
besitzen. Wenn Block nicht eindeutig, wähle den Kleineren von Beiden und
verschmelze die Blöcke. *
3 I/Os
ges. max. 4 I/Os
Beispiel Blockgröße: B = 6
By
1
2
Bx
3
7
|By| + |Bx|  2/3 B
Bz
8
10
13
Bz > By
* ggf. Indexarray aktualisieren
16.05.2016
11 /13
Implementierungsalternative
Blockarray könnte durch eine einfach/doppelt verlinkte Liste ersetzt werden.
Die daraus resultierenden Änderungen sind wie folgt:
Die Suche innerhalb eines Block hat nun eine größere Laufzeit da keine binäre
Suche möglich ist.
ABER
Das Aufrücken der Elemente bei Insert(x) und nach Delete(x) geschieht in
O(1).
 Keine Änderung der I/O – Anzahl, aber Änderung der Laufzeit
16.05.2016
12 /13
Quellen
U. Meyer, P. Sanders und J. Sibeyn (Eds.), Algorithms for Memory Hierarchies,
Advances Lectures, Lecture Notes in Computer Science 2625, Springer 2003
• Kapitel 2: R. Pagh: Basic External Memory Data Structures
16.05.2016
13 /13