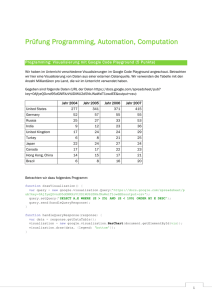
ppt

Endliche Automaten
Einführung in den Themenbereich
Karin Haenelt
18.04.2010
1
Inhalt



Informelle Einführung: Was sind endliche Automaten?
 Abstrakte Automaten
 Endliche abstrakte Automaten
 Beispiele
 T ypen endlicher Automaten
 Akzeptoren, Transduktoren
 deterministisch, nicht-deterministisch, stochastisch
Definitionen
 Abstrakte Automaten als mathematische Strukturen
 Endliche abstrakte Automaten
Einordnung endlicher Automaten
 Automatentheorie: Art des Speichers
 Theorie formaler Sprachen: Strukturelle Komplexität
© Karin Haenelt,
Endliche Automaten, Einführung,
V 4.1, 18.04.2010
2
Informelle Einführung
Abstrakter Automat
 ein abstrakter Automat ist ein mathematisches Modell für
einfache Maschinen/Programme, die bestimmte Probleme lösen
 beschreibt nicht einen bestimmten Automaten, sondern
gemeinsame Grundprinzipien einer Klasse von Automaten
 Grundlegende Komponenten
 Zustände
 Eingabesymbole
 Zustandsübergänge: reagiert auf Eingaben durch Übergang
in einen anderen Zustand
Zustände
3
des
Eingabe
Ausgabe
Automaten
© Karin Haenelt,
Endliche Automaten, Einführung,
V 4.1, 18.04.2010
Informelle Einführung
Endlicher abstrakter Automat
 Ein abstrakter Automat ist ein „endlicher Automat“, wenn die
Anzahl der Zustände, der Eingaben u. der Ausgaben endlich ist
 Komponenten der Modelle
 endliche Menge von Zuständen (Q)
 interne Konfigurationen, in denen sich ein System
befinden kann
 zeitliche Ordnung (δ)
 definiert die möglichen Sequenzen von Zuständen
 endliche Menge von Eingaben (Σ)
 endliche Menge von Ausgaben (Reaktionen) (Δ)
 System zeigt abhängig vom aktuellen Zustand eine bestimmte
Reaktion und geht in einen Folgezustand über
© Karin Haenelt,
Endliche Automaten, Einführung,
V 4.1, 18.04.2010
4
Endliche Automaten: Beispiele
Kippschalter und Lexikon
drücken
aus an
an aus
drücken
Schalter
Start
aus
an
drücken
Lexikon
0
d
1
e
2
m
n
r
s
© Karin Haenelt,
Endliche Automaten, Einführung,
V 4.1, 18.04.2010
3
4
s
5
e
6
n
7
0
1
2
3f
4f
5
6
7f
d e m n r s
1
2
3 3 3 4
5
6
7
5
Typen endlicher Automaten





i
p
 q
Akzeptoren
 Automaten ohne Ausgabe
Transduktoren
 Automaten mit Ausgabe
deterministisch
 jedem Paar [p,i] ist ein Paar [o,q]
eindeutig zugeordnet
nicht-deterministisch
 einem Paar [p,i] können mehrere
mögliche Paare [o,q] zugeordnet sein
stochastisch
 jedem Paar [p,i] ist für ein Paar [o,q]
ein Wahrscheinlichkeitsmaß zugeordnet
© Karin Haenelt,
Endliche Automaten, Einführung,
V 4.1, 18.04.2010
i:o
p 
 q
p
o
i
p
o1
i
o2
i
p
q
q1
q2
o1/w1
q1
i
o2/w2
q2
i
6
Typen endlicher Automaten
Beispiele
Akzeptor
d
0
0
S 1
t q
2
S 1
t
2
S
t
7
6
a 3
t
deterministisch
4 t 5
6
t
7
Transduktor
0 S 1 t
[t]
[ʃ]
q
2
a 3  4
[a]
[t]
nicht-deterministisch
a 3 d 4 t
d 4 t
5

[t]
0 S 1 t q
2 a 3
[t]
[a]
[ʃ]
a 8 t 9 t 10
t 6 t

[t]
dt
tt
5
7
stochastisch
d/.65 4 t/1 5
d/.65 4 t/1 5

[t]
0 S/1 1 t/1 q
0 S/1 1 t/1 q
2 a/1 3
2 a/1 3
[t]
[a]
[ʃ]
t/.35 6 t/1 7
t/.35 6 t/1 7
[t]

© Karin Haenelt,
Endliche Automaten, Einführung,
V 4.1, 18.04.2010
7
Inhalt



Informelle Einführung: Was sind endliche Automaten?
 Abstrakte Automaten
 Endliche abstrakte Automaten
 Beispiele
 T ypen endlicher Automaten
 Akzeptoren, Transduktoren
 deterministisch, nicht-deterministisch, stochastisch
Definitionen
 Abstrakte Automaten als mathematische Strukturen
 Endliche abstrakte Automaten
Einordnung endlicher Automaten
 Automatentheorie: Art des Speichers
 Theorie formaler Sprachen: Strukturelle Komplexität
© Karin Haenelt,
Endliche Automaten, Einführung,
V 4.1, 18.04.2010
8
Definitionen Abstrakte Automaten als
mathematische Strukturen: Historie
 David A. Huffman (1954), George H. Mealy (1955) und Edward
F. Moore (1956)
 untersuchten Schaltkreise
 beschrieben voneinander unabhängig den konventionellen
deterministischen Automaten in ähnlichen Varianten
 Huffman entwickelte den Begriff des abstrakten Automaten
 Mealy und Moore führten abstrakte Automaten als
mathematische Strukturen ein.
© Karin Haenelt,
Endliche Automaten, Einführung,
V 4.1, 18.04.2010
9
Definitionen
Mathematische Struktur
 Eine Struktur  ist eine Zusammenfassung einer Menge und
ausgewählter interessanter Eigenschaften dieser Menge
 Relationen, Funktionen und/oder
 ausgezeichnete Elemente
 die Eigenschaften definieren eine Struktur auf der Menge
 Darstellung als Tupel  = (Menge,
Relation1, …, Relationo,
ausgezeichnetes Element1, .., Ep)
 Beispiel (ℕ, +,×, 0,1)
 Name dieser Beispielstruktur in der abstrakten Algebra: Semiring
 Semiringe spielen in der Theorie endlicher Automaten eine
grundlegende Rolle
© Karin Haenelt,
Endliche Automaten, Einführung,
V 4.1, 18.04.2010
10
Definitionen
Determinierter abstrakter Automat
Mengentheoretische Definition (Version: Starke 1.1)
determinierter abstrakter Automat (Starke 1969: 22)
A = (X, Y, Z, γ) heißt determinierter abstrakter Automat, falls
a) X, Y, Z beliebige nichtleere Mengen sind, und
b) γ eine auf Z  X definierte Funktion ist, deren Werte in Y 
Z liegen. ■
Interpretation
X Menge der Eingabesymbole
Y Menge der Ausgabesymbole
Z Menge der Zustände
© Karin Haenelt,
Endliche Automaten, Einführung,
V 4.1, 18.04.2010
Z×X
0
a
b
Y×Z
Y×Z
A
B
1
1
11
Definitionen
Determinierter abstrakter Automat
Mengentheoretische Definition
(Version: Starke 1.2 = Version Mealy 1955)
determinierter Mealy-Automat (Starke 1969: 22)
Ein determinierter Automat A = (X, Y, Z, γ) heißt determinierter
Mealy-Automat, falls für alle x X, zZ,
γ(z,x) = [λ(z,x),δ(z,x)] ist,
wobei λ die Ergebnis und δ die Überführungsfunktion von A
ist. ■
Interpretation
X Menge der Eingabesymbole
Y Menge der Ausgabesymbole
Z Menge der Zustände
© Karin Haenelt,
Endliche Automaten, Einführung,
V 4.1, 18.04.2010
λ(z,x )
δ(z,x )
a
b
a
b
0 A
B
0 1
1
12
Defintionen
Nichtdeterministischer und stochastischer Automat
Mengentheoretische Definition
nichtdeterministischer Automat (Starke 1969: 121)
B = (X, Y, Z, h) heißt nicht-deterministischer Automat, falls
a) X, Y, Z nichtleere Mengen sind, und
b) h eine eindeutige Abbildung von Z  X in *(Z  Y) ist. ■
(Starke 1969: 121)
stochastischer Automat (Starke 1969: 211)
C = (X, Y, Z, H) heißt stochastischer Automat, wenn
a) X, Y, Z beliebige nichtleere Mengen sind, und
b) H eine auf Z  X definierte Funktion ist, die diskrete
Wahrscheinlichkeitsmaße über Y  Z als Werte H(z,x) hat
■
© Karin Haenelt,
Endliche Automaten, Einführung,
V 4.1, 18.04.2010
13
Definitionen
Endlicher Automat
Mengentheoretische Definition
endlicher determinierter Automat (Starke 1969: 25)
Ein determinierter Automat A = [X,Y,Z,δ,λ] heißt X-endlich, Yendlich bzw. Z-endlich bzw. (X,Y)-endlich usw., wenn die
jeweils angegebenen Mengen endlich sind. (X,Y,Z)-endliche
Automaten bezeichnen wir schlechthin als endlich ■
(X,Y,Z)-endliche nichtdeterministische Automaten …endlich.
(X,Y,Z)-endliche stochastische Automaten … endlich.
© Karin Haenelt,
Endliche Automaten, Einführung,
V 4.1, 18.04.2010
14
Definitionen
Mengentheoretische Notation endlicher Automaten
– eine Standardnotation
EA = (Q,q0,F,Σ,Δ,,δ,σ,ρ)
p,q  Q
q0  Q
FQ
i Σ
o Δ
w 
δ(p,i) = q
Zustände
Startzustand
Endzustände
Gewicht
Ausgabesymbol
w/ o
p
q
Eingabesymbole
i
Ausgabesymbole Zustand
Folgezustand
Eingabesymbol
Gewichte
Zustandsübergangsfunktion
σ(p,i,q) = o Ausgabefunktion
ρ(p,i,o,q) = w Gewichtungsfunktion
© Karin Haenelt,
Endliche Automaten, Einführung,
V 4.1, 18.04.2010
15
Inhalt



Informelle Einführung: Was sind endliche Automaten?
 Abstrakte Automaten
 Endliche abstrakte Automaten
 Beispiele
 T ypen endlicher Automaten
 Akzeptoren, Transduktoren
 deterministisch, nicht-deterministisch, stochastisch
Definitionen
 Abstrakte Automaten als mathematische Strukturen
 Endliche abstrakte Automaten
Einordnung endlicher Automaten
 Automatentheorie: Art des Speichers
 Theorie formaler Sprachen: Strukturelle Komplexität
© Karin Haenelt,
Endliche Automaten, Einführung,
V 4.1, 18.04.2010
16
Einordnung endlicher Automaten
Automatentheorie
Klassifikation von Algorithmen nach der Art des Speichers
• klassifiziert Algorithmen nach der Art des Speichers, der für die
Implementierung zum Merken von Zwischergebnissen
gebraucht wird
Automat
Speziali- Turingmaschine
sierungen linear beschränkter Automat
Kellerautomat (Push Down
Automaton)
endlicher Automat
© Karin Haenelt,
Endliche Automaten, Einführung,
V 4.1, 18.04.2010
Speicher
unendlich großer Speicher
endlich großer Speicher
Kellerspeicher (Stack)
kein zusätzlicher Speicher
17
Einordnung endlicher Automaten
Automatentheorie
Endliche Automaten haben kein Gedächtnis


Mengen der Zustände, der Eingabesignale, der Ausgabesignale sind
endlich
kein Gedächtnis zur Speicherung durchlaufener Zustände:
 Übergang von Zustand zur Zeit t in Zustand zur Zeit t+1 nur
abhängig von
 Zustand zur Zeit t und
 Eingabe im Zustand zur Zeit t
 Vorhergehende Zustände nur dadurch wirksam, dass
 sie über eine bestimmte Eingabe in den aktuellen Zustand
geführt haben, und
 dieser aktuelle Zustand ein bestimmtes Ergebnis repräsentiert.
Start
© Karin Haenelt,
Endliche Automaten, Einführung,
V 4.1, 18.04.2010
B
B
u
Bu
c
Buc
h Buch
18
Einordnung endlicher Automaten
Theorie formaler Sprachen
mit endlichen Automaten ist die Klasse der regulären
Sprachen erkennbar und generierbar
Sprachklassen nach struktureller Komplexität (Chomsky-Hierarchie)
Sprachklasse
rekursiv
aufzählbare
Sprachen
kontextsensitive
Sprachen
kontextfreie
Sprachen
reguläre
Sprachen
Hierarchie Grammatik
Regelformat

Typ 0
allgemeine
Regelgrammatik   
Automat
TuringMaschine
Typ 1
kontextsensitive  1 A 2   1 2
Grammatik
 
Typ 2
kontextfreie
Grammatik
reguläre
Grammatik
Typ 3
A 
A  wB

Aw 
Endlicher
rechtsline ar Automat
A  Bw 

Aw 
linkslinea r
A, B nonterminale Symbole
 Ketten aus Terminalen und Non  Terminalen
© Karin Haenelt,
Endliche Automaten, Einführung,
V 4.1, 18.04.2010
linear
beschränkter
Automat
Kellerautomat
w terminale Ketten
19
Äquivalenzen: Endliche Automaten, reguläre
Sprachen, reguläre Ausdrücke
Reguläre Ausdrücke
de([mnrs]|“ssen“)
sind äquivalent
spezifizieren
Reguläre Sprachen
Endliche Automaten
0
d
1
e
2
m
3
n
r
s
e
s
n
5
7
4
6
© Karin Haenelt,
Endliche Automaten, Einführung,
V 4.1, 18.04.2010
akzeptieren
{dem, den, der, des, dessen}
20
Literatur


Hopcroft, John E. Rajeev Motwani und Jeffrey D. Ullman (2001). Einführung in die
Automatentheorie, Formale Sprachen und Komplexität. Pearson Studium
engl. Original: Introduction to Automata Theory, Languages and Computation. AddisonWesley.
Hopcroft, John E. und Jeffrey D. Ullman (1988). Einführung in die Automatentheorie,
formale Sprachen und Komplexitätstheorie. Bonn u. a.: Addison-Wesley, 1988 (engl.
Original Introduction to automata theory, languages and computation). [Anm.: Diese
Fassung enthält die Beweise]

Huffman, D. A. (1954). The synthesis of sequential switching circuits. J. Franklin
Inst. 257: 3-4, S. 161-190 und 275-303

Lawson, Mark V. (2005). Finite automata. In: Hritsu-Varsakelis, D. und W.S.Levine (Hg).:
Handbook of networked and embedded Control Systems.
Lawson, Mark V. (2004). Finite Automata. In: D. Hristu-Varsakelis and W. S. Levine (eds.):
Handbook of networked and embedded control systems


Mealy, George H. (1955). A method for synthesizing sequential circuits. Bell
System Technical Journal 34:5, 1045-1079

Moore, Edward F. (1956). Gedanken experiments on sequential machines. In: Automata
Studies, S. 129-153, Princeton: Princeton University Press
Starke, Peter H. (1969). Abstrakte Automaten. VEB Deutscher Verlag der Wissenschaften:
Berlin (ältere, aber sehr gute mathematische Darstellung)

© Karin Haenelt,
Endliche Automaten, Einführung,
V 4.1, 18.04.2010
21
Copyright







© 2009 Karin Haenelt.
All rights reserved. The German Urheberrecht shall be applied to these slides. In
accordance with these laws these slides are a publication which may be quoted and used
for non-commercial purposes, if the bibliographic data is included as described below.
Please quote correctly. If you use the presentation or parts of it for educational and scientific
purposes, please include the bibliographic data (author, title, date, page, URL) in your
publication (book, paper, course slides, etc.).
Deletion or omission of the footer (with name, data and copyright sign) is not permitted
Bibliographic data. Karin Haenelt (2010). Endliche Automaten. Einführung in den
Themenbereich. Kursfolien 18.4.2010
http://kontext.fraunhofer.de/haenelt/kurs/folien/Haenelt_FSA-IntroV4.pdf
Any further use requires the prior permission in writing from the author.
For commercial use: No commercial use is allowed without written permission from the
author. In case you are interested in commercial use please contact the author.
Court of Jurisdiction is Darmstadt.
© Karin Haenelt,
Endliche Automaten, Einführung,
V 4.1, 18.04.2010
22
Versionen






v 4.1- 18.04.2010, v 4.0 – 30.03.2009
V03.01 – 16.04.2008
V03.00 – 12.04.2008
V02.03 - 14.04.2007
V02.02 - 11.04.2007
V02.01 - 15.04.2006
© Karin Haenelt,
Endliche Automaten, Einführung,
V 4.1, 18.04.2010
23