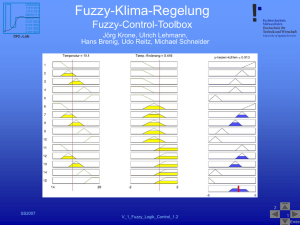
Bewertung
Werbung
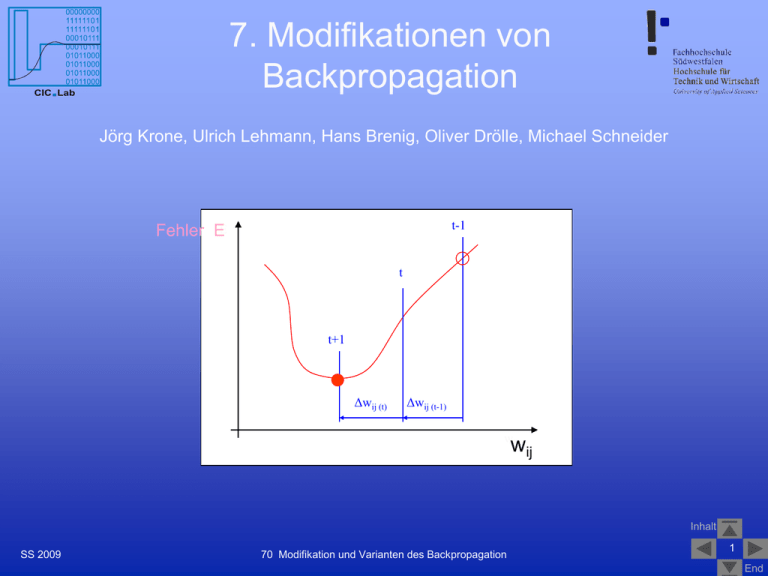
7. Modifikationen von Backpropagation CIC Lab Computational Intelligence and Control Laboratory Jörg Krone, Ulrich Lehmann, Hans Brenig, Oliver Drölle, Michael Schneider t-1 Fehler EE t t+1 Δwij (t) Δwij (t-1) wij wij Inhalt SS 2009 70 Modifikation und Varianten des Backpropagation 1 End Inhalt CIC Lab Computational Intelligence and Control Laboratory a. Motivation für die Entwicklung von Trainingsverfahren b. Momentum-Term c. Flat-Spot Elimination d. Weight Decay e. Manhatten-Training f. SuperSAB - Schrittweitenadaption Quickprop g. Resilient Propagation (Rprop) h. Levenberg-Marquardt (LM) i. Zusammenfassung j. Quellenangabe SS 2009 70 Modifikation und Varianten des Backpropagation Inhalt 2 End Motivation CIC Lab Computational Intelligence and Control Laboratory Verbesserung der Trainingsverfahren mit den Zielen: schneller – finde die neuen optimalen Gewichte möglichst schnell. Denn für sehr große Netze (>1000 Neuronen) oder viele Trainingsdatensätze kann das Training immer noch Stunden dauern genauer – finde das globale Minimum für den Fehler E. Steigerung der Genauigkeit für die Produktionsphase sicher konvergierend (stabiles Ergebnis) Inhalt SS 2009 70 Modifikation und Varianten des Backpropagation 3 End Visualisierung der Varianten des Backpropagation MATLAB 7.1/Demos/toolboxes/nn… Kapitel 12 CIC Lab Kapitel 12: In den Demos von MATLAB werden die Verfahren zur Verbesserung des Backpropagation-Trainings als e-Simulation für ein MLP (1-2-1) gezeigt. Computational Intelligence and Control Laboratory Sie basieren meistens auf der folgenden Fehlerkurve für je ein Gewicht w1 des Hidden- und ein Gewicht w2 des Outputlayers (unten links) die zur performanteren Visualisierung in 2D mit Höhenlinien (gelbes Koordinatensystem unten rechts) gezeigt wird: >>nnd12sd1 Ziel: Minimum des Fehlers Inhalt SS 2009 70 Modifikation und Varianten des Backpropagation 4 End Momentum-Term (MATLAB: traingdm) CIC Lab Computational Intelligence and Control Laboratory Prinzip: • Backpropagation mit Momentum-Term • wirkt wie ein Tiefpassfilter • die bereits vollzogene Gewichtsänderung zum Zeitpunkt t wird bei der Berechnung der Änderung zum Zeitpunkt t+1 mit einem Summanden berücksichtigt a wij (t) • die Stärke des Momentum-Terms bestimmt der Faktor a • wij (t+1) = oi f‘j (net j) (tj – oj) + a wij (t) • häufig im Bereich a = 0,6 bis 0,9 Inhalt SS 2009 70 Modifikation und Varianten des Backpropagation 5 End Demo: Backpropagation mit Momentum MATLAB 7.1/Demos/toolboxes/nn… CIC Lab Computational Intelligence and Control Laboratory Kapitel 12 Momentum Backpropagation – Einfluss des MomentumTerms, um das Fehlerminimum im Höhenprofil der Fehlerkurve (rotes Kreuz auf gelber Fläche) zu finden: >>nnd12mo (Starten Sie bei 12/-5) Inhalt SS 2009 70 Modifikation und Varianten des Backpropagation 6 End Momentum-Term: Bewertung CIC Lab Computational Intelligence and Control Laboratory Bewertung: Trainingsepochen (nicht -zeiten!) können dadurch gegenüber Standard-BAP z.B. für ein XOR-KNN mit 3 Layern (2-2-1) auf 1/8(!) reduziert werden Training im Plateau-Bereich einer Fehlerkurve wird beschleunigt Wahl einer geeigneten Lernrate wird etwas unkritischer, da der Momentum-Term die Gewichtsänderung im steilen Abstieg vergrößert und im Minimum verkleinert - bei zu großen Lernraten besteht immer noch die Gefahr von Oszillationen über einem lokalen Minimum - etwas erhöhte Rechenzeit für eine Trainingsepoche durch eine weiter Multiplikation und Addition für jede Gewichtsänderung Inhalt SS 2009 70 Modifikation und Varianten des Backpropagation 7 End Flat-Spot Elimination (modified sigmoid-prime function) CIC Lab Computational Intelligence and Control Laboratory Problem der Ableitung f‘j (net j) : • für sigmoide Aktivierungsfunktionen (logistische oder tanh) ist die Ableitung nahe 0 für Neuronen, die stark an (1) oder aus (0) sind f‘j (net j) = Logistische Aktivierung 1 0,9 0,8 0,7 Netzausgabe • Beispiel: logistische Aktivierungsfunktion 0,6 0,5 [0-0,25] 0,4 f '( x ) = 0,3 b * e (b*x ) (1.0 e( (b*x )) )² 0,2 0,1 0 -3 -2,5 -2 -1,5 -1 -0,5 0 0,5 1 1,5 2 2,5 3 Netzeingabe Logistisch SS 2009 70 Modifikation und Varianten des Backpropagation Logistisch' Inhalt 8 End Flat-Spot Elimination CIC Lab Computational Intelligence and Control Laboratory Prinzip: • Anheben der Ableitung der Aktivierungsfunktion um einen kleinen Betrag • Addition einer Konstanten zur Ableitung, damit die Funktion nicht 0 wird • f‘j (net j)mod = f‘j (net j) + 0,1 • damit verändert sich der Wertebereich für f‘j (net j)mod = [0,1-0,35] • Trainingszeiten können dadurch für das Encoder-Beispiel (105-10) auf die Hälfte reduziert werden Inhalt SS 2009 70 Modifikation und Varianten des Backpropagation 9 End Flat-Spot Elimination: Bewertung CIC Lab Computational Intelligence and Control Laboratory Bewertung: Trainingszeiten können dadurch z.B. für ein Encoder-KNN (ähnlich dem Decoder/DAU) mit 3 Layern (10-5-10) auf die Hälfte reduziert werden - Wirkung bei sehr großen KNN (> 1000 Neuronen) noch nicht vollständig untersucht! Inhalt SS 2009 70 Modifikation und Varianten des Backpropagation 10 End Weight Decay (Gewichtsabnahme) CIC Lab Computational Intelligence and Control Laboratory Prinzip: • neurobiologisch ist es unplausibel zu große Gewichte zuzulassen • große Erregungen (Ärger/Freude) werden am nächsten Tag abgeschwächter betrachtet • durch große Gewichte wird die Fehlerfläche steiler und stark zerklüftet • die bereits vollzogene Gewichtsänderung zum Zeitpunkt t wird bei der Berechnung der Änderung zum Zeitpunkt t+1 teilweise wieder subtrahiert - d wij (t) • die Stärke des Weight Decay bestimmt der Faktor d = 0,005 bis 0,03 • pwij (t+1) = opi pj - d pwij (t) Inhalt SS 2009 70 Modifikation und Varianten des Backpropagation 11 End Demo: Weight Decay MATLAB 7.1/Demos/toolboxes/nn… CIC Lab Computational Intelligence and Control Laboratory Kapitel 13 Effects of Decay – Einfluss des Weight-Decay-Terms, um den Wert eines Gewichtes bei fortlaufender Anpassung (hier bis zu 30 Epochen) zu begrenzen: >>nnd13edr Inhalt SS 2009 70 Modifikation und Varianten des Backpropagation 12 End Weight Decay: Bewertung CIC Lab Computational Intelligence and Control Laboratory Bewertung: Generalisierungsleistung wird durch kleine Gewichte verbessert - Vorsicht bei d > 0,03 ist geboten! Besser klein als zu groß! Inhalt SS 2009 70 Modifikation und Varianten des Backpropagation 13 End Manhattan-Training CIC Lab Computational Intelligence and Control Laboratory Prinzip: • für die Gewichtsänderung in jedem Trainingszyklus wird nicht der Betrag pi, sondern nur noch das Vorzeichen des Fehlersignals sgn (pi) berücksichtigt • die Backpropagationregel wird damit ersetzt durch die verallgemeinerte und einfache Delta-Regel pwij = opi • sgn (pi) Inhalt SS 2009 70 Modifikation und Varianten des Backpropagation 14 End Manhattan-Training: Bewertung CIC Lab Computational Intelligence and Control Laboratory Bewertung: Quasi-Normierung des Gradienten und damit der Gewichtsänderung mit geringem Rechenzeitbedarf wirkt dem Problem zu kleiner (Gradienten) Änderungen bei Plateaus entgegen wirkt dem Problem zu großer Gewichtsänderungen in steilen Schluchten entgegen - entspricht nicht mehr dem steilsten Abstieg bezüglich des quadratischen Abstandes der Fehlerfunktion, sondern der linearen Fehlerfunktion E = p Ep = pj tpj – opj Inhalt SS 2009 70 Modifikation und Varianten des Backpropagation 15 End SuperSAB-Lernregel (super self-adaptive backpropagation) CIC Lab Computational Intelligence and Control Laboratory (MATLAB: traingdx) Prinzip: • selbstadaptiver BAP mit eigener Schrittweite (Lernrate) ij für jedes Gewicht • Schrittweite wird im Verlauf des Trainings kontinuierlich angepasst (adaptiert) – ij (t+1) = ij (t) wird vergrößert, wenn E/ wij für zwei folgende Zeitschritte das gleiche Vorzeichen hat (mit Wachstumsfaktor 1,05 (...1,20) und initialer Lernrate = 0,9) – ij (t+1) = ij (t) wird verkleinert, wenn sich für E/ wij bei zwei folgenden Zeitschritten das Vorzeichen ändert (mit Schrumpfungsfaktor 0,5 (...0,7)) SS 2009 – ij (t+1) = ij (t) bleibt konstant, wenn E/ wij = 0 in einem betrachten Zeitschritt (t+1) 70 Modifikation und Varianten des Backpropagation Inhalt 16 End CIC Lab Demo: Backpropagation mit adaptiver Schrittweite MATLAB 7.1/Demos/toolboxes/nn… Computational Intelligence and Control Laboratory Kapitel 12 Variable Learning Rate Backpropagation – Einfluss der Änderung der Lernrate, um das Fehlerminimum im Höhenprofil der Fehlerkurve (rotes Kreuz auf gelber Fläche) zu finden: >>nnd12vl (Starten Sie bei 12/-5, Initial Learning Rate 10) Inhalt SS 2009 70 Modifikation und Varianten des Backpropagation 17 End SuperSAB-Lernregel: Bewertung CIC Lab Computational Intelligence and Control Laboratory Bewertung: wirkt Oszillationen und dem Verlassen von Minima entgegen (kleinere Lernrate, wenn sich das Vorzeichen der Steigung ändert) wirkt dem Problem zu kleiner (Gradienten) Änderungen bei Plateaus entgegen (keine Reduktion der Schrittweite, wenn die Steigung 0 oder sehr klein ist) Kombination mit Momentum-Term a möglich (a = 0,6 bis 0,9) SS 2009 - nicht alle großen Netze (> 100 Neuronen) erfüllen die Voraussetzung, dass Änderungen eines Gewichtes wij (t) unabhängig von Änderungen anderer Gewichte vorgenommen werden können - nur für Batch-Training stabiles Verhalten (Konvergenz) 70 Modifikation und Varianten des Backpropagation Inhalt 18 End Lernverfahren Quickprop CIC Lab Computational Intelligence and Control Laboratory Prinzip • iteratives Offline-Verfahren (Batch) zweiter Ordnung zur Bestimmung des Minimums der Fehlerfunktion in Anlehnung (Näherung) an eine Parabelform für die Fehlerkurve E(wij) • die Parabel (blau) wird bestimmt durch die Ableitung der Fehlerfunktion zum Zeitpunkt t-1 sowie zum aktuellen Zeitpunkt t und dem Abstand wij(t-1), dann kann der Scheitel der Parabel aus dem Verlauf der Ableitung berechnet werden Inhalt SS 2009 70 Modifikation und Varianten des Backpropagation 19 End Quickprop: Approximation der Fehlerfunktion CIC Lab Computational Intelligence and Control Laboratory Die Parabel (blau) wird bestimmt durch die Ableitung der Fehlerfunktion zum Zeitpunkt t-1 sowie zum aktuellen Zeitpunkt t und dem Abstand wij(t-1). Der Scheitel der Parabel (Nulldurchgang der Ableitung) kann aus dem Verlauf der Inhalt Ableitung einfach anhand der ähnlichen grauen Dreiecke berechnet werden. SS 2009 70 Modifikation und Varianten des Backpropagation 20 End Quickprop: Gewichtsänderung zum Scheitel der Parabel CIC Lab Computational Intelligence and Control Laboratory • wegen der Ähnlichkeit der schraffierten Dreiecke in der vorhergehenden Grafik gilt: mit P(t) = wij (t) als Parabelterm wij(t) S(t) = wij(t -1) S(t -1) - S(t) • für den Fall, dass S(t) = S(t-1), kann der Nenner 0 und der Ausdruck für die Gewichtsänderung unendlich werden, daher muss die Schrittweite auf den max. Wachstumsfaktor m begrenzt werden: • wij (t) <= m wij (t-1) mit m = 1,75 ... 2,25 Inhalt SS 2009 70 Modifikation und Varianten des Backpropagation 21 End Quickprop: Bestimmung der neuen Gewichte CIC Lab Computational Intelligence and Control Laboratory • bei Beginn des Offline-Lernverfahrens ist wij (t) = 0, deswegen wird mit dem Gradientenverfahren (Delta-Regel) mit Weight Decay (damit die Gewichte nicht zur groß werden und den Parabelterm übersteigen) gestartet: – wij (t) = p opi pj - d wij (t-1) G(t): Gradiententerm – mit = 0...2 und d 0,0001 • die gesamte Gewichtsänderung setzt sich aus dem Gradiententerm G(t) und dem Parabelterm P(t) zusammen – wij gesamt (t) = G(t) + P(t) – mit G(t) größer zu Beginn des Trainings und 0 im lokalen Minima und P(t) = 0 zu Beginn des Trainings und max. im lokalen Minima Inhalt SS 2009 70 Modifikation und Varianten des Backpropagation 22 End Quickprop: Bewertung CIC Lab Computational Intelligence and Control Laboratory Bewertung: schnelles Trainingsverfahren, wenn die Fehlerfunktion durch eine nach oben geöffnete Parabel approximiert werden kann und Änderungen eines Gewichtes wij (t) unabhängig von Änderungen anderer Gewichte vorgenommen werden können das Minimum der Fehlerfunktion kann bei guter Approximation schon nach einem Lernschritt nahezu erreicht werden - neigt im Online-Training wie SuperSAB zu Oszillationen (instabilem Verhalten) - Wirkung bei größeren KNN (> 100 Neuronen) wurden in einigen Anwendungen Oszillationen in lokalen Minima beobachtet! • Abhilfe: Offline-Training und (Lernrate) durch die Anzahl der eingehenden Gewichte einer Zelle teilen. Dadurch können größere Netze besser lernen! Inhalt SS 2009 70 Modifikation und Varianten des Backpropagation 23 End Rprop: Resilient Propagagtion [elastische Fehler-Rückpropagation] CIC Lab (MATLAB: trainrp) Computational Intelligence and Control Laboratory Prinzip: • basiert auf den Ideen von vorgestellten Verfahren: – Manhatten-Training: einfache Normierung der Gewichtsänderung (nur das Vorzeichen des Gradienten entscheidet nicht der Betrag) – SuperSAB: Anpassung bzw. Adaption der Lernrate an die Fehlerkurve (Wachstumsfaktor und Schrumpffaktor) – Quickprop: Verwendung der Steigung der Fehlerfunktion des aktuellen und vorherigen Zeitpunktes zur schnellen Bestimmung des Fehler-Minimums • kombiniert die Vorteile mehrerer Verfahren • ist ein Batch-Trainingsverfahren (offline) Inhalt SS 2009 70 Modifikation und Varianten des Backpropagation 24 End Rprop (1+2) CIC Lab Computational Intelligence and Control Laboratory Im folgenden werden der Betrag der Gewichtsänderung mit ij(t) und die Änderung des Gewichts wij (t) mit wij (t) bezeichnet und getrennt geändert. S(t) ist die Steigung der Fehlerkurve im Schritt t. ij(t) = ij(t-1) falls S(t-1) S(t) > 0 ij(t-1) falls S(t-1) S(t) < 0 ij(t-1) falls S(t-1) S(t) = 0 Berechnung von wij (t+1) = wij (t) + wij (t) mit: wij (t) = - ij(t) ij(t) - wij (t-1) - sign(S(t)) ij(t) falls S(t-1) S(t) > 0 oder S(t) > 0 falls S(t-1) S(t) > 0 oder S(t) < 0 falls S(t-1) S(t) < 0 sonst Inhalt SS 2009 70 Modifikation und Varianten des Backpropagation 25 End Rprop (3+4) CIC Lab Computational Intelligence and Control Laboratory Im folgenden werden der Betrag der Gewichtsänderung mit ij(t) und die Änderung des Gewichts wij (t) mit wij (t) bezeichnet und getrennt geändert. S(t) ist die Steigung der Fehlerkurve im Schritt t. ij(t) = ij(t-1) falls S(t-1) S(t) > 0 ij(t-1) falls S(t-1) S(t) < 0 ij(t-1) falls S(t-1) S(t) = 0 Berechnung von wij (t+1) = wij (t) + wij (t) mit: wij (t) = - ij(t) ij(t) - wij (t-1) - sign(S(t)) ij(t) falls S(t-1) S(t) > 0 oder S(t) > 0 falls S(t-1) S(t) > 0 oder S(t) < 0 falls S(t-1) S(t) < 0 sonst Inhalt SS 2009 70 Modifikation und Varianten des Backpropagation 26 End Rprop: Parametereinstellung CIC Lab Computational Intelligence and Control Laboratory • bei fast allen Experimenten wurden bisher folgende Werte gewählt: – Wachstumsfaktor: = 1,2 mit W-Grenzwert: m = 1,75 ... 2,25 – Schrumpffaktor: = 0,5 • zur Vermeidung von Gleitkommaüberlauf im Simulationsrechner werden meistens noch Schranken zur Beschränkung der Gewichtsänderung vorgegeben: – obere Schranke: max = 50 – untere Schranke: min = 1,0 * 10-6 (ein Mikro) • Initialisierungsgewichte ij(t=0) liegen etwa im Bereich: - 0 = 1,0 bis 4,0 • ein Weight Decay-Term kann die Generalisierungsleistung von Inhalt Rprop verbessern SS 2009 70 Modifikation und Varianten des Backpropagation 27 End Rprop: Bewertung CIC Lab Computational Intelligence and Control Laboratory Bewertung: sehr schnelles Trainingsverfahren - nur Batch-Training sinnvoll, da Online-Training noch instabiler als beim SuperSAB - Generalisierungsleistung kann schlechter sein als bei einem Netz, das mit Backpropagation trainiert wurde! • Abhilfe: Rprop mit Weight Decay-Term! Inhalt SS 2009 70 Modifikation und Varianten des Backpropagation 28 End Levenberg-Marquardt (LM) (MATLAB: trainlm) CIC Lab Computational Intelligence and Control Laboratory Prinzip: • basiert auf den Ideen von vorgestellten Verfahren: – Backpropagation-Training: Suche des Minimums der Fehlerfunktion in der Richtung des steilsten Abstiegs (Gradientenverfahren) – Quickprop: Verwendung der Steigung der Fehlerfunktion des aktuellen und vorherigen Zeitpunktes zur schnellen Bestimmung des Fehler-Minimums (nichtlineare Approximation durch Parabel) • kombiniert die Vorteile mehrerer Verfahren • ist ein Batch-Trainingsverfahren (offline) Inhalt SS 2009 70 Modifikation und Varianten des Backpropagation 29 End Levenberg-Marquardt (LM) CIC Lab Computational Intelligence and Control Laboratory • Nichtlineare Approximation der Fehlerfunktion E = f (wij) durch LM am Beispiel einer Gaußkurve mit wenigen Stützpunkten: die Summe der Abstandsquadrate wird minimiert Inhalt SS 2009 70 Modifikation und Varianten des Backpropagation 30 End Demo: Levenberg-Marquardt-Algorithmus MATLAB 7.1/Demos/toolboxes/nn… CIC Lab Computational Intelligence and Control Laboratory Kapitel 12 LM–Training: Kombination aus Gradientenabstieg und Newton-Verfahren zur Approximation der Fehlerfunktion. Bei geeigneten Parametern wird das Minimum des Fehlers (rotes Kreuz auf gelber Fläche) nach zwei Epochen gefunden: >>nnd12m (Starten Sie bei 12/-5, Initial Rate µ = 0.03 (Anteil des Gradientenverf.)) Inhalt SS 2009 70 Modifikation und Varianten des Backpropagation 31 End LM: Initialisierung der Gewichte CIC Lab Computational Intelligence and Control Laboratory Unterschiedliche Initialisierungen des KNN mit gleichem Trainingsalgorithmus können erhebliche Unterschiede in der Lernkurve haben. Inhalt SS 2009 70 Modifikation und Varianten des Backpropagation 32 End Levenberg-Marquardt: Bewertung CIC Lab Computational Intelligence and Control Laboratory Bewertung: sehr schnelles Trainingsverfahren sehr genau ↔ geringe Fehler (Training und Validierung) bei guter Initialisierung erzielbar - nur Batch-Training sinnvoll, da Online-Training instabil - Generalisierungsleistung kann schlechter sein als Backpropagation! - hoher Speicherbedarf = p • (w+) • Abhilfe: Validierung und Testdaten neben den Trainingsdaten verwenden und bei Verschlechterung des Testfehlers Abbruch des Trainings! Mehrere Initialisierungen testen (≥ 5); ggf. trainrp verwenden Inhalt SS 2009 70 Modifikation und Varianten des Backpropagation 33 End Zusammenfassung I CIC Lab Computational Intelligence and Control Laboratory Eigenschaften Trainingsverfahren Backprop (BAP) (MATLAB: traingd mit Momentum: traingdm) Backprop mit Momentum und Weight Decay Manhatten Training SuperSAB (selbstadaptives BAP) (MATLAB: traingdx) Quickprop Rprop (elastisches BAP) (MATLAB: trainrp) SS 2009 Anwendungsbreite Trainingsgeschwindigkeit Konvergenz Generalisierung Bemerkung ++ -- + ++ ++ Standardverfahren + - ++ ++ Weight Decay nach biologischem Vorbild o normierte Gewichtsveränderung, feste Schrittweite/Gitter o adaptive Lernrate, eigene Schrittweite für jedes Gewicht + näherungsweise Berechnung von E min durch Parabelapproxim. + normierte Gewichtsveränderung und Adaption an die Steigung Inhalt o + + + + ++ ++ o o o/+ o/+ 70 Modifikation und Varianten des Backpropagation 34 End Zusammenfassung II CIC Lab Computational Intelligence and Control Laboratory Eigenschaften Trainingsgeschwindigkeit Konvergenz Generalisierung Bemerkung Trainingsverfahren Anwendungsbreite Backprop (BAP) (MATLAB: traingd) ++ -- + ++ Standardverfahren + Kombination aus Backprop und Quickprop (Gradientenabstieg und Newton-Verfahren) Levenberg-Marquardt (MATLAB: trainlm) +/++ ++ ++ Inhalt SS 2009 70 Modifikation und Varianten des Backpropagation 35 End Quellenverzeichnis CIC Lab Computational Intelligence and Control Laboratory • MATLAB User's Guide Neural Network Toolbox • MATLAB Printable (PDF) Documentation on the Web • A. Zell: Simulation von neuronalen Netzen • VDE/VDI GMA FA 5.14 Computational Intelligence http://www.iai.fzk.de/medtech/biosignal/gma/tutorial/index.html • e-Simulation Levenberg-Marquardt-Algorithmus http://www.malerczyk.de/applets/Marquardt/Marquardt.html#iteration http://de.wikipedia.org/wiki/Newtonsches_N%C3%A4herungsverfahren • Levenberg-Marquardt-Algorithmus http://www.crgraph.de/Levenberg.pdf http://www.versuchsmethoden.de/ Inhalt SS 2009 70 Modifikation und Varianten des Backpropagation 36 End Fragen CIC Lab Computational Intelligence and Control Laboratory Fragen Sie bitte! Inhalt SS 2009 70 Modifikation und Varianten des Backpropagation 37 End Danke CIC Lab Computational Intelligence and Control Laboratory Vielen Dank für Ihr Interesse! Inhalt SS 2009 70 Modifikation und Varianten des Backpropagation 38 End Anlagen CIC Lab Computational Intelligence and Control Laboratory Inhalt SS 2009 70 Modifikation und Varianten des Backpropagation 39 End Rprop (1 bis 4) CIC Lab Computational Intelligence and Control Laboratory Inhalt SS 2009 70 Modifikation und Varianten des Backpropagation 40 End Danke CIC Lab Computational Intelligence and Control Laboratory Vielen Dank für Ihr Interesse! Inhalt SS 2009 70 Modifikation und Varianten des Backpropagation 41 End