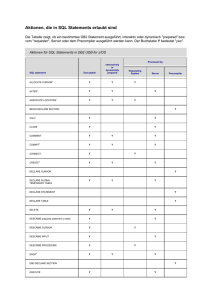
T-Invarianten-Technik

Fighting State Explosion
Using Petri net Invariants in
State Space Construction
1
Quelle
K. Schmidt:
Using Petri net Invariants in State Space
Construction
Proc. 9th Conf. Tools and Algorithms for the
Construction and Analysis of Systems
LNCS 2619: Seite 473-488, Springer, 2003
2
Überblick






Grundidee
Depth-first-Algorithmus
S-Invarianten-Technik
T-Invarianten-Technik
Praktische Versuche
Fazit
3
Überblick






Grundidee
Depth-first-Algorithmus
S-Invarianten-Technik
T-Invarianten-Technik
Praktische Versuche
Fazit
4
Grundidee
5-speisende-Philosophen-System
• 242 Zustände
5
Grundidee
• 10-Philosophen-System : 59048 Zustände
• 500-Philosophen-System: 3500-1 Zustände
• Eigenschaften wie Deadlockfreiheit werden durch Aufstellen
des Erreichbarkeitsgraphen verifiziert.
• Problem: Wie können die Zustände in einem begrenzten
Speicher gebracht werden, damit z.B. ein Algorithmus
zum Aufstellen des Erreichbarkeitsgraphen terminiert?
6
Grundidee
• mögliche Lösungsansätze:
• Die Größe der Zustände wird komprimiert.
S-Invarianten-Technik
• Die Anzahl der gespeicherten Zustände wird reduziert.
T-Invarianten-Technik
7
Überblick






Grundidee
Depth-first-Algorithmus
S-Invarianten-Technik
T-Invarianten-Technik
Praktische Versuche
Fazit
8
Depth-first-Algorithmus
var V: set of markings initial ;
var E: set of edges initial ;
var current: marking initial MN;
procedure StateGraph ()
var t: transition;
var Enabled: set of transitions:
begin
V:=V U {current};
Enabled := {t| t T  current  t - }
for t in Enabled do
E := E U [current,current+t+- t -]
current = current+t+- t -;
if current  V then
StateGraph();
fi
current = current+t - - t+ ;
done end.
// t - = W(.,t)
// t + = W(t,.)
9
Überblick






Grundidee
Depth-first-Algorithmus
S-Invarianten-Technik
T-Invarianten-Technik
Praktische Versuche
Fazit
10
S-Invarianten-Technik
Wiederholung:
• Inzidenzmatrix C(N):
•
•
jede Stelle sS einer Zeile und jede Transition tT entspricht
einer Spalte der Inzidenzmatrix
C(s,t) = W(t,s) + W(s,t)
• S-Invariante:
•
Zeilenvektor y, mit y . C(N) = 0
(0 entspricht Nullvektor)
• M  [MN  : y. M = y. MN
11
S-Invarianten-Technik
• Modifiziertes Producer-Consumer-Petrinetz
Inzidenzmatrix:
12
S-Invarianten-Technik
S-Invariante: (1,1,0,0,0,0,0,0)
13
S-Invarianten-Technik
• Ziel der S-Invarianten-Technik: Zustandskompression
Sei y eine S-Invariante mit y(s) ≠ 0 :
sS y(s) . M(s) = y. MN
y. M = y. MN
y(s) . M(s) = y. MN - s'S\{s} y(s') . M(s')
y. MN - s'S\{s} y(s') . M(s')
M(s)
=
y(s)
14
S-Invarianten-Technik
• Producer-Consumer-Beispiel:
y. MN - s'S\{s2} y(s') . M(s')
M(s2)
=
=
y(s2)
(1,1,0,0,0,0,0,0) * (1,0,0,1,1,0,0,1) - M(s1)
=
=
1 - M(s1)
1
Nach Schalten von p: M(s2) = 1 - M(s1) = 1 - 0 = 1
15
S-Invarianten-Technik
• Partitionierung der Stellenmenge S:
s2
s6
s7
R
s4
s3
s1
s5
s8
P
P = signifikante Stellen
R = redundante Stellen
S = P U R, P ∩ R = 0
für jede Stelle rR:  S-Invariante y mit y(r) ≠ 0 und r'R\{r}: y(r') = 0
Markierungen aller redundanten Stellen können durch
die Markierungen der signifikanten Stellen berechnet werden
16
S-Invarianten-Technik
• Wie erfolgt die Partitionierung der Stellenmenge S ?
1.
2.
3.
4.
5.
Inzidenzmatrix C(N) transponieren
Transponierte Matrix CT(N) in Obere-Dreiecks-Form
umwandeln
Einteilung in head- und tail-Variablen
(signifikante Stellen = head-Variablen,
redundante Stellen = tail-Variablen)
partial-assignment durchführen
(eine tail-Variable wird mit 1, allen anderen mit 0
belegt)
Gleichung CT(N) . y = 0 lösen
17
S-Invarianten-Technik
• Ergebnis:
• Bei n linear-unabhängigen S-Invarianten können n
Komponenten der Markierung weggelassen werden
• für zwei erreichbare Markierungen M und M' :
M = M'  sP: m(s) = m'(s)
18
S-Invarianten-Technik
var V: set of markings initial ;
var E: set of edges initial ;
var current: marking initial MN;
procedure StateGraph ()
var t: transition;
var Enabled: set of transitions:
begin
V:=V U {current};
Enabled := {t| t T  current  t - }
for t in Enabled do
E := E U [current,current+t+- t -]
current = current+t+- t -;
if current  V then
StateGraph();
fi
current = current+t - - t+ ;
done end.
• der aktuelle Zustand ist immer
komplett (current) bekannt
• P-Teil (current) der Markierung
wird in V und E gespeichert
• Korrektheit bleibt erhalten
• S-Invarianten müssen nicht
bekannt sein
• kleinere Vektoren beschleunigen
Suchen und Einfügen in V
19
S-Invarianten-Technik
• Nach Terminierung des Algorithmus sind folgende
Erreichbarkeitsgraphen des Producer-Consumer-Beispiel
gespeichert:
Ohne S-Invarianten Kompression
Mit S-Invarianten Kompression 20
S-Invarianten Technik
• Zusammenfassung:
•
30 – 50% einer Markierung muss nicht in die Datenstruktur
gespeichert werden
•
Laufzeitverbesserung durch Beschleunigung von Such- und
Einfügeoperationen aufgrund von geschrumpften Vektoren in der
Datenstruktur
•
Der Aufwand zur Berechnung der nötigen Informationen wird
überkompensiert.
•
Informationen können aus der Inzidenzmatrix gewonnen werden
21
Überblick






Grundidee
Depth-first-Algorithmus
S-Invarianten-Technik
T-Invarianten-Technik
Praktische Versuche
Fazit
22
T-Invarianten-Technik
• Wiederholung:
• Zustandsgleichung: M' = M + C(N) . Parikh(w)
• T-Invariante:
•
•
Ganzzahliger Spaltenvektor x, mit C(N) . x = 0
x ist trivial, wenn x = 0 gilt.
• Gilt M [w M (Zyklus), dann ist Parikh(w) eine TInvariante.
23
T-Invarianten-Technik
• Producer-Consumer-Petrinetz
Inzidenzmatrix:
24
T-Invarianten-Technik
T-Invariante: (1,1,1,1)
25
T-Invarianten-Technik
• Ziel der T-Invarianten-Technik: Zustandsreduktion
• Jedoch müssen so viele Zustände gespeichert werden,
damit der depth-first-Algorithmus terminiert.
• Zyklen gefährden das Terminieren des depth-firstAlgorithmus
• Mindestens ein Zustand jedes Zyklus muss
abgespeichert werden.
26
T-Invarianten-Technik
Gesucht ist eine Menge Z  [MN von Zuständen, so
dass jeder Zyklus im Erreichbarkeitsgraphen
mindestens eine Markierung in Z hat.
• Jeder Zyklus kann durch eine T-Invariante ausgedrückt
werden
• Ermittle Menge U von Transitionen, wobei U
mindestens eine Transition jeder nicht trivialen TInvariante hat und somit mindestens eine Transition
jedes Zyklus enthält.
27
T-Invarianten-Technik
U
T-Invariante x
a
T-Invariante y
T-Invariante z
b
c
Erreichbarkeitsgraph
• jeder Zyklus im Erreichbarkeitsgraph hat einen Zustand, der mit einer
Kante versehen ist, die mit einer Transition aus U gekennzeichnet ist.
28
T-Invarianten-Technik
Die Menge von Zuständen, bei denen
mindestens ein Element aus U aktiviert wird,
erfüllt die Anforderungen von Z.
29
T-Invarianten-Technik
• Wie findet man die Menge U ?
•
Für jede T-Invariante x gilt: C(N) . x = 0
•
C(N) wird in Obere-Dreiecks-Form gebracht
•
Wird allen tail-Variablen die 0 zugeordnet, so wird der 0-Vektor
als Lösung berechnet.
•
keine T-Invariante hat bei allen tail-Variablen eine 0.
Menge U
= Menge der tail-Variablen
30
T-Invarianten-Technik
• Wie findet man die Menge U ?
1. Inzidenzmatrix C(N) aufstellen
2. C(N) in Obere-Dreiecks-Form umwandeln
3. Einteilung in head- und tail-Variablen
vornehmen
4. Die Menge der tail-Variablen bilden U.
31
T-Invarianten-Technik
var V: set of markings initial ;
var current: marking initial MN;
var depth: integer initial 0;
procedure TStateGraph ()
var t: transition;
var Enabled: set of transitions:
begin
Enabled := {t| t T  current  t - }
if Enabled ∩ U ≠  or depth mod k = 0
then V:=V U {current};
fi
for t in Enabled do
current = current+t+- t -;
depth := depth + 1;
if current  V then
TStateGraph();
fi
current = current+t - - t+ ;
depth := depth - 1;
done end.
32
T-Invarianten-Technik
Ursprünglicher Erreichbarkeitsgraph
Abgespeicherte Zustände
33
T-Invarianten Technik
• Zusammenfassung:
• Erheblich weniger Speicheraufwand nötig
• Laufzeit-Speicher-Verhältnis durch Variable k
konfigurierbar
• T-Invarianten müssen nicht berechnet werden
• Informationen können aus der Inzidenzmatrix
gewonnen werden
34
Überblick






Grundidee
Depth-first-Algorithmus
S-Invarianten-Technik
T-Invarianten-Technik
Praktische Versuche
Fazit
35
Praktische Versuche
• S-Invarianten-Technik:
• n-Philosophen-System: 5n Stellen, 2n linear unabhängige SInvarianten
gespeicherter Vektor um 40% reduziert
• Laufzeit:
10 phil
Zustände
59048
Zeit (sec) ohne Reduktion
2.7
Zeit (sec) mit Reduktion
2.1
11 phil
117146
9.8
7.7
12 phil
531440
37.7
30.3
36
Praktische Versuche
• T-Invarianten-Technik:
5 phil
Zustände ohne Red.
242
Zeit (sec) ohne Red.
0.03
Zustände mit Red. (k=5000) 160
Zeit (sec) mit Red. (k=5000) 0.09
Zustände mit Red. (k=20)
186
Zeit (sec) mit Red. (k=20)
0.05
Zustände mit Red. (k=10)
201
Zeit (sec) mit Red. (k=10)
0.04
6 phil
728
0.04
530
0.7
591
0.1
629
0.07
7 phil
2186
0.08
1708
9.7
1828
0.36
1947
0.19
8 phil
6560
0.23
5417
136.0
5664
3.19
5984
0.59
9 phil
19682
0.76
16952
2177.6
17545
10.8
18289
1.8
37
Praktische Versuche
• T-Invarianten-Technik in Kombination mit partial order reduction:
Zustände mit partial order reduction
Zeit (sec) mit partial order reduction
Zustände mit beiden Red. (k=5000)
Zeit (sec) mit beiden Red. (k=5000)
Zustände mit beiden Red. (k=20)
Zeit (sec) mit beiden Red. (k=20)
Zustände mit beiden Red. (k=10)
Zeit (sec) mit beiden Red. (k=10)
100 phil
29702
2.2
10311
45.3
14502
3.5
17702
2.8
200 phil
119402
16.4
41093
395.3
59002
26.5
71402
21.4
38
Überblick






Grundidee
Depth-first-Algorithmus
S-Invarianten-Technik
T-Invarianten-Technik
Praktische Versuche
Fazit
39
Fazit
• S-Invarianten-Technik:
•
•
•
•
Verbesserung in Speicherbedarf und Laufzeit
Kompatibel zu anderen Techniken
Keine besondere Vorsicht bei Einsatz notwendig
In den Programmen LoLA, INA verwendet
40
Fazit
• T-Invarianten-Technik:
•
•
•
•
Als „standalone“-Technik nicht geeignet
Wertvoll in Kombination mit anderen Techniken
Parameter k muss sinnvoll gewählt werden
In dem Programm UPPAAL verwendet
41
Vielen Dank
für die
Aufmerksamkeit !!!
42