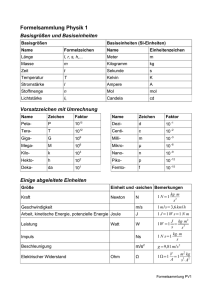
Musterlösung

Musterlösung
1.) a) VaR 1 (0,99)  - ( - (0,99)  )
VaR 1 (0,95)  - ( - (0,95)  )
p = w*100/G
w = VaR2
G = VaR1
p=
 (100.000  1,64  800.000)  100 1.212.000

 68,71
 (100.000  2,33  800.000)
1.764.000
100 - 68,71 = 31,29
Neeson kann durch das falsche Reporting 31,29% Kapital einsparen.
 p x (1  p) N  x
b) LR POF  2 ln  x
Nx
 p̂ (1  p̂)



N = 24(!!), x = 2, p = 0,01
LR POF




 0,012  0,99 22 
 0,0000802 
 2 ln 
 2 ln 
  2 ln( 0,078)  5,094  3,84
2
22 
0,00102 
2
2





    1   
 24

    24  
Leesons Reporting wirkt unglaubwürdig, da der POF-Test die Nullhypothese "99%-Quantil"
ablehnt.
c) μGes = 100.000 + 60.000 = 160.000
σGes =
800.000 2  600.000 2  2  800.000  600.000  (0,31)  838.093,074
 VaR(0,99) = -(160.000 - 2,33*838.093.074) = 1.792.756,86 €
 VaR(0,95) = -(160.000 - 1,64*838.093.074) = 1.214.472,64 €
p
1.214.472,64  100
 67,74
1.792.756,86
100  67,74  32,26
Neeson kann jetzt 32,26% durch das falsche Reporting einsparen
d) 4331² = 18757561 (1)
7575² = 57380625 (2)
3806² = 14485636 (3)
4856² = 23580736 (4)
5807² = 33721249 (5)
7212² = 52012944 (6)
129² = 00016641 (7)
166² = 00027556 (8)
275² = 00075625 (9)
756 (10)
e) Menschen - Fehler, die von Menschen verursacht werden, z.B. Betrug
Prozesse - Prozessschwächen wie schlechtes Management
Systeme - Systemfehler, z.B. Computerausfall
Exterene Ereignisse - z.B. Feuer, Naturkatastrophen
Neeson fällt unter die Kategorien "Menschen" und "Prozesse".
2.) a) c  S0  (d 1 )  k  e  rt  (d 2 ) (Black-Scholes-Formel)
d1 
S
ln  0
 k
  2
   r 
2
 
 t

 t
 , d  d  t
2
1
S0  32
k = 30
σ = 0,2
t = 1/3
r = 0,03
0,2 2  1
 32  

ln     0,03 
2  3
 32  
d1 
 0,70325
1
0,2 
3
d 2  0,70325  0,2
1
 0,58778
3
c  32  (d1 )  30  e
0, 03
1
3
 (d 2 )  32  0,533  30  0,99  0,222  10,496
Der faire Preis der Option beträgt 10,50 €.
b) Gleiche Rechnung wie in a), nur mit σ = 0,3 und t = 1/6
d1 = 0,629
d2 = 0,5065
c = 10,046
Der neue Preis beträgt nun 10,05 €.
c) (jeweilige Formel siehe Formelblatt)
 c (Delta) - Veränderung des Optionspreises bei Veränderung des Aktienkurses
c (Gamma) - Veränderung des Delta bei Veränderung des Aktienkurses
 c (Vega) - Veränderung des Optionspreises bei Veränderung der Volatilität
 c (Theta) - Veränderung des Optionspreises bei Veränderung der Restlaufzeit
c (Rho) - Veränderung des Optionspreises bei Veränderung des Zinssatzes
d)  c  (d1 )  0,533
Ä    c  500  266,5
Der perfekte Hedge wird bei einer Shortposition von ca. 267 Anteilen des Underlying
erreicht. (Falsche Tabelle, daher nicht die richtige Lösung, aber volle Punktzahl bei dieser
Antwort.)
3.) a)  Ges  U11  U 2  2  U 3 3  50.000  0,127  40.000  0,0402  10.000  0,1456  9414
2
 Ges
 U12 1,1  U 22  2, 2  U 32 3,3  2U1 U 2 1, 2  2U1 U 31,3  2U 2 U 3 2,3
2
 Ges   Ges
 50.000 2  2,3198  40.000 2  0,801  ...  98.420,88
VaR (0,99)  ( Ges  (0,99)   Ges )  (9414  2,33  98.420,88)  219.906,65 €
Der Value-at-Risk beträgt 219.906,65€.
1 1 1


b) i. 1 1 1
1 1 1


Perfekte pos. Korrelation bedeutet, dass die Kovarianz zwischen je zwei Elementen 1
beträgt.
1 0 0


ii.  0 1 0 
0 0 1


Bei Unabhängigkeit ist die Kovarianzmatrix die Einheitsmatrix.
wahr
Bei der Sensitivitätsanalyse wird das Risiko durch Veränderungen der Marktparameter
falsch
x
beschrieben. Richtig. Siehe Folien Teil 1.
x
Der faire Preis eines europäischen Calls liegt immer unter dem aktuellen Marktpreis.
Falsch. Kann leicht bei hoher Volatilität erreicht werden.
x
Der faire Preis eines europäischen Calls liegt immer unter dem Strikepreis. Falsch.
Kann leicht bei hoher Laufzeit erreicht werden
Aktienrenditen sind häufig linksschief und zeitlich korreliert. Richtig, so genannte
x
Stylized Facts von Aktienreturns.
x
Das Marktrisiko des Handelsbuches einer Universalbank auf Gesamtbankebene weist
so genannte "Fat-Tails" auf. Falsch. Auf Gesamtbankebene ist das Portfolio durch
Diversifikationseffekte und den zentralen Grenzwertsatz wieder normalverteilt.
x
Unter Hedging versteht man den Abschluss einer risikoneutralen Position. Falsch.
Hedging bedeutet das Risiko einer Position zu neutralisieren durch eingehen einer
Gegenposition.
Der Expected Shortfall ist der Erwartungswert der VaR-Überschreitungen. Richtig.
x
Das Kreditrisiko einer Universalbank hat einen größeren Anteil auf das Risikoprofil
x
einer Bank als Marktrisiko und operationelle Risiken zusammen. Richtig.
Bei der Clusteranalyse spielt der Begriff der "Distanz" eine wichtige Rolle. Richtig.
x
x
Beim OpRisk-Basisindikatoransatz wird die Bank in acht Geschäftsfelder unterteilt.
Falsch. Dies wird beim Standardansatz getan.
x
Ausschlaggebender Indikator beim OpRisk-Standardansatz ist das Nettoeinkommen.
Falsch. Es ist das Bruttoeinkommen.
x
Die Datensammlung für Marktrisiko und operationelles Risiko ist sehr ähnlich. Falsch.
Marktdaten liegen allgemein vor, OpRisk Daten müssen von Hand gesammelt werden.
x
Dr. Pawlik berichtete über Marktrisiken bei der Hypovereinsbank. Falsch, das war Dr.
Auer.
Fitch Ratings ist die weltweit drittgrößte Ratingagentur. Richtig.
Der Vortrag der Deutschen Bank musste leider ausfallen. Falsch. Das war der SAP
Vortrag.
x
x