Beispiel: ZR – eine Sprache für einen Zeichenroboter

Sächsisches Bildungsinstitut, F+T-Zentrum Meißen
SBI00643 Fachbezogene Fortbildung für
Fachberater im Fach Informatik an
Gymnasien
„Theoretische Informatik (TI) – Theoretische Grundlagen
von Programmiersprachen“ mit der Lernumgebung AtoCC
Meißen, 09.04.-11.04.08
Christian Wagenknecht, Michael Hielscher
Das Wichtigste zuerst!
2
Vielen Dank an
Herrn Wolfgang Rafelt
Erster Kontakt: 25.05.07
Zeitplan und Ziele
3
Mittwoch, 09.04.08,
15:00-17:30: Einführung, Installation, ZR-Compiler (TDiag)
Donnerstag, 10.04.08,
09:00-10:30: Formale Grammatik für ZR inkl. Grundbegriffe (kfGEdit)
11:00-12:30: DEA für Zahl und Farbwert (AutoEdit), reguläre Ausdrücke
13:30-15:00: DKA für kfS (AutoEdit), Beispiel: WH n [...]
15:15-17:30: Compiler = Analyse + Synthese (VCC)
Analyse: Scanner, Parser; Zielsprache: PS; TDiagramm
Freitag, 11.04.08,
09:00-10:30: Projekt "Notensprache" – Quellsprache, Zielsprache,
Werkzeuge; Übersetzungsmodell, Grammatiken, reduzierte Gramm.
11:00-12:30: DEA, reguläre Ausdrücke, Compiler, TDiag (Projektende)
13:30-14:00: Turingmaschinen, Hinweis auf Automaten mit Ausgabe
(Mealy-, Moore-Automaten, nicht LP-Gegenstand)
Ende des Kurses
Lehrplan  Ziele und Inhalte
4
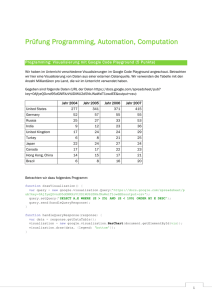
In den meisten Bundesländern sind ausgewählte Inhalte der TI
Lehrplaninhalt der Sek. II:
Nr. Bundesland
1
Baden-Württemberg
2
Bayern
Berlin
Brandenburg
3
4
Lehrplaninhalt (Lernbereich)
Bereich der theoretischen Informatik
(Automaten, Berechenbarkeit)
3. Formale Sprachen (noch Entwurf)
4.4 Sprachen und Automaten
4.4 Sprachen und Automaten
Grundlagen der Theoretischen Informatik
5 Bremen
(Automaten, formale Sprachen)
Formale Sprachen, endliche Automaten,
6 Hamburg
Kellerautomaten, Scanner, Parser,
Ableitungsbaum
Formale Sprachen und Grammatiken
7 Hessen
Automaten, Fakultativ: Übersetzerbau
8 Mecklenburg-Vorpommern 4.4 Sprachen und Automaten
Eigenschaften endlicher Automaten
9 Niedersachsen
Aspekte formaler Sprachen
10 Nordrhein-Westfalen
Endliche Automaten und formale Sprachen
11 Rheinland-Pfalz
12 Saarland
13 Sachsen
14 Sachsen-Anhalt
15 Schleswig-Holstein
16 Thüringen
Formale Sprachen und Automaten zur
Sprachbeschreibung und Spracherkennung
Automaten und formale Sprachen
Fakultativ: Übersetzerbau
8 A: Formale Sprachen, Kellerautomat, Akzeptor
Endliche Automaten und formale Sprachen
Automaten als mögliches Themengebiet
Themenbereich 7.3: Einblick in formale Sprachen
Pflichtbestandteil
nein
ja (auch GK)
Ja (auch GK)
nein
nein
ja (auch GK)
ja (auch GK)
nein
nein
ja (nur LK)
ja (auch GK)
nein
nein
nein
nein
Lehrplanauszug Hessen
5
Verbindliche Unterrichtsinhalte/Aufgaben:
Formale Sprachen und
Grammatiken
reguläre und kontextfreie Grammatiken und Sprachen
Anwendung mit Syntaxdiagrammen
Chomsky-Hierarchie (LK)
kontextsensitive Sprachen (LK)
Endliche Automaten
Zustand, Zustandsübergang, Zustandsdiagramm Zeichen, Akzeptor
Simulation realer Automaten (z. B. Getränkeautomat)
Anwendung endlicher Automaten (z. B. Scanner)
deterministische und nicht-deterministische Automaten (LK)
reguläre Ausdrücke (LK)
Mensch-Maschine-Kommunikation (LK)
Kellerautomaten
(LK, GK fakultativ)
Automat mit Kellerspeicher
kontextfreie Grammatiken
Klammerausdrücke, Rekursion
Turing- oder registerberechenbar
Churchsche These
Computer als universelle symbolverarbeitende Maschine
Verhältnis Mensch-Maschine
Turing- oder Registermaschine
(LK, GK fakultativ)
Fakultative Unterrichtsinhalte/Aufgaben:
Übersetzerbau
Scanner, Parser, Interpreter und Compiler
z. B. Steuersprache für Roboter, LOGO, Plotter oder miniPASCAL
Lernbereich 8 A (Sächs. Lehrplan)
6
endlicher Automat
GK Informatik f. Jahrgangsstufen 11 und 12, wird ab Schuljahr 2008/09 wirksam
TI-Inhalte in der Schulinformatik:
Probleme und Chancen
7
 Blick in die Lehrpläne verschiedener Bundesländer
• totale Überfrachtung mit Fachinhalten
• Formulierung von Wunschvorstellungen (z.B. TI + Compiler)
(geringe didaktische Erfahrung)
• Besondere Spezifik der TI (mathematische Denktechniken
vs. ingenieurwissenschaftlicher Arbeitskontext der SE) wird
nicht ausreichend berücksichtigt
 Inhalts/Zeit-Relation
 Verinnerlichung von Inhalten
 Kompetenz und Motivation des Lehrpersonals
Gefühlssituation der Lehrenden
8






"TI wollte ich nie machen."
"TI hat mich nie richtig interessiert."
"TI war mir immer zu theoretisch und abstrakt."
"Die TI-Dozenten waren suspekt – TI im
postgradualen Studium erinnere ich mit
Grausen."
"Die TI-Inhalten helfen mir nicht, wenn das
Schulnetzwerk mal wieder zusammenbricht."
...
TI-Inhalte in der Schulinformatik:
Probleme und Chancen
9
 Zeit-Problem, Inhalte-Problem (Zusammenfassung von oben)
 Manche Lehrende mögen es nicht. – Motivationsproblem
 Manche Lehrende können es nicht richtig. Qualifikationsproblem
 SchülerInnen/Studierende fragen gelegentlich: "Wann geht es
denn nun endlich richtig los mit der Informatik? Ach so, das ist
es schon."  - Vermittlungsproblem
"Ergebnis": Wenn möglich, TI weglassen. FALSCH!!!
Chance: Informatik als Wissenschaft repräsentieren!
(wie Mathematik und Naturwissenschaften)
Sonst: Studienabbrecher als konkrete Folge!!!
Didaktische Software für TI
10
 in Schulen:
diverse Simulationstools oder Lernumgebungen, wie
Kara; meist von enthusiastischen LehrerInnen entwickelt
 in Hochschulen:
Systeme für die Lehre,
wie JFLAP
LEX und YACC für die
Hand des Ingenieurs
Simulationstool – Bildungsserver Hessen
Unsere Ziele – nicht ohne AtoCC!!!
11
1. Belastbare Motivation für TI-Inhalte durch herausfordernde
Start-Fragestellung mit Praxisrelevanz und Modellierung
eines Zielsystems (Sprachübersetzer) am Anfang
2. Vermittlungs-/Anwendungszyklen für TI-Wissen mit Projektbezug (Praxis nicht als "Anhängsel" zur Theorie)
3. Komplexe Anwendung von TI-Inhalten auf sehr hohem
Abstraktionsniveau (automatisierte Compiler-Generierung),
Rückkehr zur und Konkretisierung der Modellierungsebene
Behauptung: Dabei ist AtoCC ein unverzichtbares Hilfsmittel.
Beispiel: ZR – eine Sprache für einen Zeichenroboter
12
Praxisnahe (echte!) Aufgabe mit grafischer (akustischer) Ausgabe:
Entwickeln Sie einen Compiler, der die Sprache ZR (ZeichenRoboter) in
PDF übersetzt. (Schülergerecht formulieren!)
Eingabewort (in ZR):
WH 36 [WH 4 [VW 100 RE 90] RE 10]
Sprachelemente:
VW n
VorWärts n Schritte
RE n
Rechts um n Grad
WH n [ ... ] WiehderHole n-mal [...]
FARBE f
StiftFARRBE f
STIFT n
Strichstärke n
Aufgabe: Verwenden Sie den fertigen Compiler zr2pdf blume.zr
(konsole.bat aufrufen, blume.zr ansehen)
Beispiel: ZR – eine Sprache für einen Zeichenroboter
13
Der Zeichenroboter kann auch mehr: BunteBlume.zr
Beispiel: ZR – eine Sprache für einen Zeichenroboter
14
Weiterer Ablauf:
1. Modellierung der Problemlösung mit TDiag
2. Syntax-Definition von ZR: formale Grammatik, Ableitungsbaum mit kfGEdit
3. Parser  Akzeptoren  Automatenmodelle (EA, KA) mit AutoEdit
4. Arbeitsteilung: Scanner, Parser
5. Zielsprachenbezug  automatisierte Compiler-Entwicklung mit VCC
6. Teilsysteme werden in Modellierung eingebracht (TDiag)
7. Ergebnis: lauffähiger (nichttrivialer) Übersetzer, den man benutzen kann!
TDiag, kfGEdit, AutoEdit, und VCC sind Bestandteile von AtoCC.
Beispiel: ZR – eine Sprache für einen Zeichenroboter
15


Wir wollen zunächst den Übersetzungsprozess
entwerfen modellieren
Verwendung von T-Diagrammen:
 T-Diagramme bestehen aus 4 Bausteintypen.
 Compilerbaustein, Programmbaustein,
Interpreterbaustein und Ein/Ausgabe-Baustein
Compiler
Programm
Interpreter
Ein/Ausgabe an
Programmbaustein
Beispiel: ZR – eine Sprache für einen Zeichenroboter
16
T-Diagramm: 1. Entwurf
ZR2PDF möchte niemand schreiben!!!
Beispiel: ZR – eine Sprache für einen Zeichenroboter
17
T-Diagramm: 2. Entwurf
ZR2PS werden wir entwickeln, PS2PDF
und Acrobat Reader wird vom System
bereitgestellt.
Beispiel: ZR – eine Sprache für einen Zeichenroboter
18
Nachdem wir nun wissen, wie unser Compiler später zur
Übersetzung eingesetzt werden soll, wenden wir uns der
Entwicklung des Compilers zu.
Sprache näher betrachten
 Terminale und Nichtterminale festlegen
 formale Grammatik definieren
 Ableitungsbäume erzeugen

Beispiel: ZR – eine Sprache für einen Zeichenroboter
19
Betrachten wir die Sprache ZR und versuchen
wir ihren Aufbau zu beschreiben:
 VW
50
 RE 270
 RE 45 WH 2 [VW 100]
 WH 4 [VW 100 RE 100]
 WH 36 [WH 4 [VW 100 RE 90] RE 10]
 Magnetkarten an der Tafel
Beispiel: ZR – eine Sprache für einen Zeichenroboter
20

Beschreiben wir den Baustein Zahl genauer:
0
soll in ZR keine Zahl sein, da VW 0 oder RE 0
keine Veränderung herbeiführen.
 Vorangestellte Nullen, wie bei 0815, wollen wir
auch nicht erlauben.

Ergänzen wir unsere Grammatik um:
Zahl
Ziffern
Ziffer
ErsteZiffer
 ErsteZiffer Ziffern
 Ziffer Ziffern | 
 0 | 1 | ... | 9
 1 | 2 | ... | 9
Beispiel: ZR – eine Sprache für einen Zeichenroboter
21
Beispiel: ZR – eine Sprache für einen Zeichenroboter
22
Beispiel: ZR – eine Sprache für einen Zeichenroboter
23
Beispiel: ZR – eine Sprache für einen Zeichenroboter
24
Programm
 Anweisungen
Anweisungen  Anweisung Anweisungen | EPSILON
Anweisung
 VW Zahl
| RE Zahl
| WH Zahl [ Anweisungen ]
| FARBE Farbwert
| STIFT Zahl
Farbwert
 rot | blau | gruen | gelb | schwarz
Zahl
 ErsteZiffer Ziffern
Ziffern
 Ziffer Ziffern | EPSILON
Ziffer
 0 | 1 | ... | 9
ErsteZiffer
 1 | 2 | ... | 9
Kontextfreie Grammatik
25
Grammatikdefinitionen immer vollständig angeben! G=(N,T,P,s)
kfG, d.h. Regeln haben die Gestalt X  b, mit |x|  |b|
Hinweis auf Chomsky-Hierarchie (s. TI-Vorlesungen);
Grammatik-Transformationen in Betracht ziehen
Hervorzuhebendes Problem bei kfG: Mehrdeutigkeit;
Eingabewort: if a1 then if a2 then s1 else s2
S -> if E then S | if E then S else S | s1 | s2
E -> a1 | a2
Lösung:
S -> S1 | S2
S1 -> if E then S1 else S1 | s1 | s2
S2 -> if E then S | if E then S1 else S2
E -> a1 | a2
Dangling else
Beispiel: ZR – eine Sprache für einen Zeichenroboter
26
Automaten als Akzeptoren für Sprachen
Akzeptor prüft, ob ein Wort zur Sprache gehört oder
nicht. (Keine Ausgabe  Wort akzeptiert)
(Thema: Programmiersprachen und Syntaxfehler)
 Wir nehmen zwei Ausschnitte aus den Produktionen:

Zahl
Ziffern
Ziffer
ErsteZiffer
 ErsteZiffer Ziffern
 Ziffer Ziffern | EPSILON
 0 | 1 | ... | 9
 1 | 2 | ... | 9
Anweisungen
Anweisung
 Anweisung Anweisungen | EPSILON
 VW Zahl | WH Zahl [ Anweisungen ]
Beispiel: ZR – eine Sprache für einen Zeichenroboter
27
Kleiner Sprachausschnitt:
Zahl
 ErsteZiffer Ziffern
Ziffern
 Ziffer Ziffern | EPSILON
Ziffer
 0 | 1 | ... | 9
ErsteZiffer
 1 | 2 | ... | 9
Beispiel: ZR – eine Sprache für einen Zeichenroboter
28
Übungsaufgabe
29
1.
2.
Geben Sie eine (reguläre) Grammatik für die
Sprache der Uhrzeiten an.
Entwerfen/Erzeugen Sie einen Automaten.
Vorgehen (allgemein):
Beispielwörter, Beispiel-Nichtwörter, Muster, Muster
spezifizieren, Grammatik entwerfen, Beispielwörter
testen, Grammatik "justieren" bzw. transformieren bzw.
nach alternativer Idee neu entwerfen, Automat
generieren (hier: regGr  NEA  DEA)
Lösung der Übungsaufgabe
30
Muster: ab : cd, a=0,1,2; b=0,1,2,3,4,5,6,7,8,9, wenn a=0,1
b=0,1,2,3, wenn a=2
c=0,1,2,3,4,5; d=0,1,2,3,4,5,6,7,8,9
U -> A : C
A -> 0 B | 1 B | 2 Q
B -> 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
Q -> 0 | 1 | 2 | 3
C -> 0 B | 1 B | 2 B | 3 B | 4 B | 5 B
... ist nicht regulär (Prüfknopf in kfGEdit) – erste Regel!
(aber eine schöne kfG)
Lösung der Übungsaufgabe
31
Regelbildung – rechte Seiten: Erstes Zeichen (Terminal) und Rest (Nichtterminal)
U -> 0 H | 1 H | 2 K
H -> 0 B | 1 B | 2 B | 3 B | 4 B | 5 B | 6 B | 7 B | 8 B | 9 B
B -> : C
C -> 0 Z | 1 Z | 2 Z | 3 Z | 4 Z | 5 Z
Z -> 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
K -> 0 R | 1 R | 2 R | 3 R
R -> : C
Vollständige Definition angeben! s. kfGEdit
Lösung der Übungsaufgabe
32
DEA für die Sprache der Uhrzeiten: regGr  NEA  DEA
Lösung der Übungsaufgabe
33
Ein zugehöriger NEA ist konzeptionelle wesentlich übersichtlicher,
erfordert aber eine grundlegende Behandlung des Nichtdeterminismus.
Beispiel: ZR – eine Sprache für einen Zeichenroboter
34
Anweisungen  Anweisung Anweisungen | EPSILON
Anweisung
 VW n
| WH n [ Anweisungen ]
DKA für obigen Grammatik-Ausschnitt
Beispiel: ZR – eine Sprache für einen Zeichenroboter
35
Beispiele für DKA und NKA
36
Musterbeispiele:
1. Sprache der Palindrome über {0,1}
2. Sprache der Palindrome über {0,1} mit (durch !) markierter Wortmitte
Für 1 gibt es keinen DKA, für 2 NKA und DKA.
Studienaufgabe: DKA für a n b n (n>0).
Beispiele für DKA und NKA
37
Lösung:
Sprache der Palindrome über {0,1} mit (durch !) markierter Wortmitte
Beispiel: ZR – eine Sprache für einen Zeichenroboter
38


Aus der Kombination von kleinen endlichen
Automaten und einem Kellerautomaten wird später
unser Compiler bestehen.
Für EA-Sprachen können auch reguläre Ausdrücke
verwendet werden:
Beispiel Zahl (nicht 0, ohne Vornullen): [1-9][0-9]*
Reguläre Ausdrücke für reguläre Sprachen
39
Reguläre Ausdrücke für reguläre Sprachen
40
Reguläre Ausdrücke für reguläre Sprachen
41
Reguläre Ausdrücke zur Definition regulärer Sprachen
Zahlen in ZR: [1-9][0-9]*
Aktuelle Syntax von RegExp ist dem Gebrauch als Filter in vielen PS
angepasst. Z.B. [...] Zeichenauswahl – genau ein Zeichen aus ...
s. Arbeitsblatt: Reguläre Ausdrücke in Programmiersprachen.pdf
Achtung:
Rückwärtsreferenzen führen aus der Klasse der regulären Sprachen
heraus.
Arbeitsweise des Compilers
42
Arbeitsweise eines Scanners
43
Ein- und Ausgabe des Scanners:
Quelltext besteht aus
Zeichen und der
Rechner weiß noch
nicht wie diese
zusammengehören.
Viele kleine endliche
Automaten
entscheiden welche
Schlüsselworte im
Quelltext stehen.
Token als Paare
[Tokenname, Lexem]
z.B.:
[Wiederhole, "WH"]
[Zahl, "12"]
[KlammerAuf, "["]
Beispiel: ZR – eine Sprache für einen Zeichenroboter
44
 Anweisungen
Programm
Anweisungen  Anweisung Anweisungen | EPSILON
Anweisung
 VW Zahl
| RE Zahl
| WH Zahl [ Anweisungen ]
| FARBE Farbwert
| STIFT Zahl
Farbwert
: rot|blau|gruen|gelb|schwarz
Zahl
: [1-9][0-9]*
Reguläre Grammatik  NEA  DEA
45
farbwert.txt
Beispiel: ZR – eine Sprache für einen Zeichenroboter
46
Endliche Automaten (RegExp) für alle unsere Terminale:
KlammerAuf
: \[
KlammerZu
: \]
Wiederhole
: WH
Rechts
: RE
Vor
: VW
Stift
: STIFT
Farbe
: FARBE
Farbwert
: rot|blau|gruen|gelb|schwarz
Zahl
: [1-9][0-9]*
S, T, I, F, T
Beispiel: ZR – eine Sprache für einen Zeichenroboter
47
Beispiel: ZR – eine Sprache für einen Zeichenroboter
48
per Hand ergänzen
Arbeitsweise des Parsers
49
Ein- und Ausgabe des Parsers:
Beinhaltet die
aufgetretenen
Terminale der
Grammatik des
Parsers
Grammatik von ZR in
Form eines
Kellerautomaten 
Prüft ob Wort zur
Sprache gehört
#false erfolgt
meinst durch
Ausgabe von
„Syntax Error“
Beispiel: ZR – eine Sprache für einen Zeichenroboter
50

Entwicklung des ZR2PS Compilers in VCC
Übertragen der EA in die Scannerdefinition
 Übertragen der vereinfachten Grammatik in die
Parserdefinition
 Entwickeln so genannter S-Attribute für die
Zielcodegenerierung

Beispiel: Postscript als Zielsprache des ZR-Compilers
51
ZR  PS  PDF
Eingabewort (in ZR):
WH 36 [WH 4 [VW 100 RE 90] RE 10]
Ausgabewort (in PS):
%!PS-Adobe-2.0
/orient 0 def /xpos 0 def /ypos 0 def
0 0 0 setrgbcolor
/goto { /ypos exch def /xpos exch def xpos ypos moveto} def
/turn { /orient exch orient add def} def
/draw { /len exch def newpath xpos ypos moveto
/xpos xpos orient sin len mul add def
/ypos ypos orient cos len mul add def
xpos ypos lineto stroke
} def
300 400 goto
100 draw 90 turn 100 … turn 10 turn
Beispiel: Zielcodegenerierung für ZR
52

Zielcodegenerierung:
 Der
Compiler soll PostScript erstellen nicht nur
#true und #false ausgeben.
 Entwicklung von S-Attributen
 S-Attribute sind kleine Quelltextfragmente die für
jede rechte Regelseite definiert werden können.
 Wird eine Regel angewendet wird auch das
entsprechende Quellcodefragment ausgeführt.
Beispiel: ZR – eine Sprache für einen Zeichenroboter
53
Die Platzhalter $1 bis $n:
 In S-Attributen verwenden wir Platzhalter für die
Ergebnisse der einzelnen Regelbausteine.
Eingabewort sei: VW 20 RE 10
$1
$2
VW
20
$$ = "20 draw "
 Von einem Token ist $n immer
des Lexem des Tokens !
 Von einem Nichtterminal ist $n
immer das Ergebnis $$ des
Nichtterminals !
Beispiel: ZR – eine Sprache für einen Zeichenroboter
54
Die Platzhalter $1 bis $n:
 In S-Attributen verwenden wir Platzhalter für die
Ergebnisse der einzelnen Regelbausteine.
Eingabewort sei: WH 4 [ VW 20 ]
$1
$2
$3
$4
$5
WH
4
[
20 draw
]
$$ = "20 draw 20 draw 20 draw 20 draw "
 Von einem Token ist $n immer
des Lexem des Tokens !
 Von einem Nichtterminal ist $n
immer das Ergebnis $$ des
Nichtterminals !
 Alle $n und $$ sind vom Datentyp
String !!!
Arbeitsweise des Compilers
55
WH 36 [WH 4 [VW 100
RE 90] RE 10]
[Wiederhole, "WH"]
[Zahl, "12"]
[KlammerAuf" "["]
…
%!PS-Adobe-2.0
/orient 0 def /xpos 0 def /ypos 0 def
0 0 0 setrgbcolor
/goto { /ypos exch def /xpos exch
def xpos ypos moveto} def
…
Programm
 Anweisungen
Anweisungen  Anweisung Anweisungen | 
Anweisung
 VW Zahl
| RE Zahl
| WH Zahl [ Anweisungen ]
| FARBE Farbwert
| STIFT Zahl
Beispiel: ZR – eine Sprache für einen Zeichenroboter
56

Anwenden des Compilers auf der
Modellierungsebene der T-Diagramme in TDiag.
Beispiel: Musiksprache
57

Das Beispiel soll Ihnen die
Möglichkeit geben, die
gezeigten Inhalte noch einmal
selbst anzuwenden.

Ein Beispiel für sehr einfache
Musiksprachen sind ältere
Handyklingeltöne.
Beispiel für Musiksprachen
58

http://www.audio-ware.com/midi/codingworkshop-ringtone-converter.htm
Die Musiksprache ML
59
 Wir wollen unsere eigene
Notensprache entwickeln für
monophone Lieder (nur eine
Stimme)
 Programmbeispiel:
C1-2 G1-8 A0-4 A0-8
G0-4 G0-8 C0-8 P-2
Die Musiksprache ML
60
 Die Sprache ist so einfach,
dass sie sogar regulär ist.
 Eine etwas komplexere
Sprache könnte etwa
Wiederholungen enthalten:
[C1-2 G1-8 [A0-4 A0-8]] P-2
(typisches Klammerbeispiel für
Kellerautomaten)
Die Musiksprache ML
61
 Erforschen Sie ML:
 Öffnen Sie den Ordner„Songs“ und starten Sie
Console.bat
Aufgabe: Ändern Sie den Inhalt einer
ML Datei um sich besser mit ML vertraut
zu machen.
Vorgehensmodell
62
Software entwickeln
Implementierungsebene
Modellebene
Problemebene
Software nutzen
Entwicklung eines ML Interpreters
63
Lösungsschritte:
1)
Ein T-Diagramm erstellen
2)
Eine formale Grammatik für ML erstellen
3)
Eine Scanner- und Parserdefinition entwickeln
4)
S-Attribute für die Regeln im Parser aufstellen
5)
Den ML Interpreter generieren lassen
6)
Den Interpreter mit Hilfe des T-Diagramms testen
Arbeitsblatt 1
Ein T-Diagramm für den ML Interpreter
64

Verfassen Sie ein T-Diagramm für den ML
Interpreter (geschrieben in Java Bytecode)
welcher auf ein ML Programm angewendet wird.
Ein T-Diagramm für den ML Interpreter
65
Eine Grammatik für ML erstellen
66



Den mittleren Teil des Diagramms (den ML
Interpreter) wollen wir herstellen.
Dafür müssen wir den Aufbau (Syntax) von ML
beschreiben. Wir verwenden eine kontextfreie
Grammatik GML (in BNF).
Betrachten wir einfache Beispiele der Sprache
und leiten eine Grammatik ab:
 G0-4
G1-2 A0-1
 D1-32 P-16 A-8 P-2
 C0-16 C1-8 F0-1 H1-2 P-1
Beginnen Sie mit:
Song  Notes
Notes  ?
Eine Grammatik für ML erstellen
67
Eine Grammatik für ML erstellen
68
Eine Grammatik für ML erstellen
69
Einen Interpreter für ML entwickeln
70

Prinzipell können wir sagen, dass ein Interpreter
sehr ähnlich wie ein Compiler arbeitet. Er erstellt
nur keinen Zielcode.

Wir werden deshalb im Folgenden einen
Compiler herstellen, denn wir als Interpreter
verwenden wollen.
Wie funktioniert ein Interpreter ?
71
Für einen Interpreter
wollen wir keine
Ausgabe
 wir wollen direkt
Befehle ausführen.
Einen Interpreter für ML entwickeln
72





Wir müssen den Scanner und Parser
beschreiben wie diese arbeiten sollen.
Wir beginnen mit der Scannerdefinition.
Wir definieren Tokenklassen mit Expressions
(Pattern – RegExp.)
Einfachste Lösung: Für jedes Terminal in GML
verwenden wir genau eine Tokenklasse.
Komplexe Pattern erleichtern aber die Arbeit
des Parsers später erheblich.
 wir versuchen dem Scanner auch Arbeit
zu geben 
Einen Interpreter für ML entwickeln
73
KeyName
C|D|E|F|G|A|H
all keynames
Octave
0|1
1
allowed octaves
Duration
1
1|2|4|8|16|32
duration values
(full, half, ¼, …)
Tokenklassen
Liste
Einen Interpreter für ML entwickeln
74



Wir müssen dafür sorgen,
dass sich Tokenklassen
nicht überlappen.
In echten Programmiersprachen ist das aber
häufig der Fall:
Keyword: begin
Identifier: [a-z]+
Um dieses Problem zu
lösen ist die Reihenfolge
der Tokenklassen wichtig!
KeyName
C|D|E|F|G|A|H
Token0
0
Token1
1
Token2_32
2|4|8|16|32
Minus
\-
Pause
P
Einen Interpreter für ML entwickeln
75

Wir können eine vereinfachte Grammatik
G’ML unter Verwendung der Token erstellen:

Wir haben 6 Tokenklassen:
KeyName, Token0, Token1, Token2_32, P
und -
Einen Interpreter für ML entwickeln
76

Wir können die RegExp. der Tokenklassen
auch wieder durch endliche Automaten
darstellen:
Token2_32
2|4|8|16|32
KeyName
C|D|E|F|G|A|H
Einen Interpreter für ML entwickeln
77
Einen Interpreter für ML entwickeln
78
Wir bennen die
Tokenklassen
sinnvoll um.
Einen Interpreter für ML entwickeln
79
Die regulären
Ausdrücke müssen
eingetragen werden.
Einen Interpreter für ML entwickeln
80
Einen Interpreter für ML entwickeln
81

Wir können jetzt einen Compiler erstellen
lassen (Scanner + Parser) und auf ein
Programm in ML anwenden:

Wir wollen aber Töne abspielen
 es fehlt also noch etwas 
Einen Interpreter für ML entwickeln
82


Für jede Regel müssen wir ein S-Attribut
erstellen.
Erinnerung:
S-Attribute sind kleine Quelltextfragmente die
bei der Anwendung einer Regel ausgeführt
werden.
Jede Regel liefert ihr Ergebnis in $$ zurück
indem das Quelltextfragment abgearbeitet wird
(wir müssen $$ bei Bedarf einen Wert
zuweisen).
Einen Interpreter für ML entwickeln
83
Wiederholung Platzhalter $1 bis $n:
 In S-Attributen können wir Platzhalter verwenden, die
jeweils für das Ergebnis eines Elements auf der rechten
Regelseite stehen.
C1-4
Input word: C1-8 D1-4
$1
$2
$2
C1
-
8
$$ = "C1-8"
 Von einem Token $n ist dies
immer das Lexem!
 Von einem Nichtterminal ist $n
immer dessen Ergebnis $$!
Einen Interpreter für ML entwickeln
84
Wiederholung Platzhalter $1 bis $n:
 In S-Attributen können wir Platzhalter verwenden, die
jeweils für das Ergebnis eines Elements auf der rechten
Regelseite stehen.
C1-4
Input word: C1-8 D1-4
 Von einem Token $n ist dies
immer das Lexem!
 Von einem Nichtterminal ist $n
immer dessen Ergebnis $$!
$1
C1
$1
$2
C
1
$$ = "C1"
 Alle $n und $$ haben den
Datentyp String !!!
Einen Interpreter für ML entwickeln
85



Nun können wir uns den S-Attributen
zuwenden für:
Was passiert wenn die Regel Note…
auftritt?
Auf Arbeitsblatt 1 finden wir 3 Hilfsfunktionen um
MIDI Noten in Java abzuspielen.
Wir müssen den Notennamen wie C0 in die
entsprechende MIDI Taste übersetzen und
playNote aufrufen.
Einen Interpreter für ML entwickeln
86
Einen Interpreter für ML entwickeln
87
 Wir erstellen erneut den
Interpreter
Das T-Diagramm ausführen
88
Einen MLSVG Compiler entwickeln
89
Lösungsschritte:
1)
Ein T-Diagramm erstellen
2)
Eine Scanner- und Parserdefinition erstellen
3)
S-Attribute für die Regeln im Parser aufstellen
4)
Den MLSVG Compiler generieren lassen
5)
Den Compiler mit Hilfe des T-Diagramms testen
Arbeitsblatt 2
Ein T-Diagramm für den MLSVG
Compiler erstellen
90
Einen MLSVG Compiler entwickeln
91
Das T-Diagramm ausführen
92

Wir können unseren Compiler dem TDiagramm zuweisen und dieses ausführen:
Zusammenfassung
93
C1-8 E1-4 D0-2 …
[KeyName, "C"]
[Token1, "1"]
[Minus, "-"]
…
<?xml version="1.0" ?>
<!DOCTYPE svg PUBLIC "//W3C//DTD SVG
20010904//EN"
"http://www.w3.org/TR/2001/RE
C-SVG-...
Turing-Maschine (EINE Definition)
94
Turing-Maschine
95
Aufbau und Arbeitsweise: TM-Modell
TM als Akzeptor:
Start: auf erstem Zeichen des Eingabewortes
Stopp: per crash (falls die TM überhaupt anhält)
Turing-Maschine
96
Beispiel:
a n bn cn , mit n  0
Didaktische Kommentierung:
ECHTE Beispiele sind
problematisch.
Turing-Maschine in der Berechenbarkeitstheorie
97
Hinweis auf das Buch
98
Wagenknecht, Chr.; Hielscher, M.:
Sprachen, Automaten und Compiler:
Ein Arbeitsbuch zur theoretischen Informatik.
Teubner, 2008