Physik und Umwelt – Lerneinheit 4 3 KKP-1 und KKP

Physik und Umwelt – Lerneinheit 4
Physik und Umwelt – Lerneinheit 4
Einführung in die Atom- und Kernphysik
KKP-1 und KKP-2 Philippsburg, Bildquelle: Fachzeitschrift atw, Ausgabe 06/2009
Dieter Bangert
März 2016
3
Inhaltsverzeichnis – Physik und Umwelt - LE 4: Atom- und Kernphysik
Inhaltsverzeichnis – Physik und Umwelt - LE 4: Atom- und Kernphysik
1
Atomphysik ................................................................................................................ 5
1.1
Wellen und Photonen ....................................................................................................... 6
1.2
1.2.1
1.2.2
Quantentheorie und Bohrsches Atommodell ................................................................. 13
Quantenzahlen ............................................................................................................... 20
Atombau und das Periodensystem der Elemente.......................................................... 28
1.3
Atomspektren: Strahlungsabsorption und -emission ..................................................... 34
1.4
Laser ............................................................................................................................... 38
1.5
1.5.1
1.5.2
Röntgenstrahlung ........................................................................................................... 42
Röntgenbremsstrahlung ................................................................................................. 43
Charakteristische Röntgenstrahlung .............................................................................. 44
1.6
Übungsaufgaben zu Kapitel 1 ........................................................................................ 45
1.7
Musterlösungen zu Kapitel 1 .......................................................................................... 47
2
Kernphysik ............................................................................................................... 52
2.1
Aufbau der Atomkerne.................................................................................................... 52
2.2
Kernkraft und Bindungsenergie ...................................................................................... 52
2.3
2.3.1
2.3.2
Radioaktivität .................................................................................................................. 62
Das radioaktive Zerfallsgesetz ....................................................................................... 65
Radioaktive Umwandlungsreihen ................................................................................... 67
2.4
Kernreaktionen ............................................................................................................... 68
2.5
Kernspaltung und Kernfusion ......................................................................................... 71
2.6
Wechselwirkung ionisierender Strahlung mit Materie .................................................... 78
2.7
Nachweismethoden für ionisierende Strahlung ............................................................. 82
2.8
Strahlenschutz ................................................................................................................ 85
2.9
Übungsaufgaben zu Kapitel 2 ........................................................................................ 94
2.10
Musterlösungen zu Kapitel 2 .......................................................................................... 95
Anhang 1: Physikalische Konstanten.................................................................................................. 98
Anhang 2: Formelzeichen ................................................................................................................... 99
Anhang 3: Periodensystem der Elemente (IUPAC).......................................................................... 102
4
1.1 Wellen und Photonen
1
Atomphysik
Die Vorstellung einer atomaren Struktur der stofflichen Materie geht
auf die griechischen Philosophen Demokrit von Abdera (um 460 –
370 v. Chr.) und Leukipp von Milet (um 500 – 440 v. Chr.) zurück.
Sie spekulierten, dass die Materie aus kleinsten unteilbaren Teilchen,
den Atomen (grch. atomos = das Unteilbare) besteht. Den ersten
wissenschaftlichen Beweis für die Richtigkeit dieser Atomhypothese
lieferte 1807 der englische Naturforscher John Dalton (1766 – 1844).
Die Atomvorstellung von Dalton beruhte auf einem BillardkugelModell. Demnach stellte man sich die Atome als kleinste, massebehaftete, undurchdringliche Kugeln vor. Mit dieser Modellvorstellung
war Dalton in der Lage, die bei chemischen Reaktionen beobachteten
Gesetzmäßigkeiten zu beschreiben, z. B. die Tatsache, dass sich zwei
Elemente in ein und derselben Verbindung immer im gleichen Massenverhältnis vereinigen. Eigentlicher Vorläufer der Atomphysik war
dann die in der 2. Hälfte des 19. Jahrhunderts intensiv betriebene
Gasentladungsphysik. Dabei wurden in einem evakuierten Glaskolben zwei Metallelektroden eingeschmolzen und der Kolben mit einer
kleinen Gasmenge gefüllt. Beim Anlegen einer elektrischen Spannung an die beiden Elektroden wurde ein Stromfluss durch den Gasraum beobachtet, der i. A. mit Leuchterscheinungen verbunden war.
In solchen Gasentladungsröhren wurden aufgrund ihrer unterschiedlichen Ablenkung im Magnetfeld elektrisch positiv geladene Kanalstrahlen und negativ geladene Kathodenstrahlen entdeckt. Die Kanalstrahlen konnten als positiv geladene Gasionen identifiziert werden.
Die genauere Untersuchung der Kathodenstrahlen führte 1897 zur
Entdeckung des Elektrons durch Joseph John Thomson (1856 –
1940). Kathodenstrahlen sind somit Elektronenstrahlen, und Atome
lassen sich in Bestandteile zerlegen, sind also zusammengesetzte
Teilchen. Die grundlegende Theorie der Atomphysik ist die Quantenmechanik. Sie gestattet eine genaue mathematische Berechnung
der atomphysikalischen Vorgänge. Ihre philosophische Interpretation
ist allerdings bis heute kontrovers geblieben. Einer der Mitbegründer
der Quantenmechanik, der dänische Physiker Niels Bohr (1885 –
1962), hat dazu folgende Bemerkung gemacht: “Wer glaubt, sie verstanden zu haben, zeigt damit nur, dass er sie nicht einmal ansatzweise begriffen hat.“
Die Atomphysik beschäftigt sich mit den Vorgängen in den Elektronenhüllen der Atome. Das nachfolgende Kapitel soll einen elementaren Einblick in dieses Teilgebiet der modernen Physik liefern.
5
1 Atomphysik
1.1
Wellen und Photonen
Der englische Physiker James Clerk Maxwell (1831 – 1879) hatte in
seiner Theorie der Elektrizität vorausgesagt, dass sich elektrische
und magnetische Felder wellenartig im Raum ausbreiten können.
1887 gelang es Heinrich Hertz (1857 – 1894) die Existenz solcher
elektromagnetischer Wellen experimentell nachzuweisen. Damit
wurde klar, dass Lichtstrahlen elektromagnetische Wellen sind. Aus
den in Gasentladungsröhren auftretenden Leuchterscheinungen
konnte geschlossen werden, dass die Atome die Quelle dieser Lichtstrahlen sind.
Die Beschreibung von Vorgängen im submikroskopischen Bereich
der Atome und Atomkerne ist Aufgabe der Quantenphysik. Sie weist
beispielsweise monochromatischem Licht, einer elektromagnetischen
Wellenerscheinung mit der Wellenlänge λ , Frequenz f und Ausbreitungsgeschwindigkeit c auch eine Teilcheneigenschaft zu. Dabei gilt
für elektromagnetische Strahlung:
λ ⋅f = c .
(1.1)
In Abbildung 1.1 ist eine unendlich ausgedehnte monochromatische
r
Lichtwelle dargestellt. Dabei steht der elektrische
Feldvektor E senkr
recht auf dem magnetischen Feldvektor B . Beide Vektorfelder variieren periodisch mit der Zeit t und stehen senkrecht auf der Ausbreir
tungsrichtung c der Lichtwelle.
Abb. 1.1: Monochromatische Lichtwelle
Bei der graphischen Darstellung einer elektromagnetischen Welle
kann der Verlauf des elektrischen oder magnetischen Feldes zu einem bestimmten Zeitpunkt an verschiedenen Orten dargestellt werden. Man erhält dann eine Ortsraumdarstellung. Die Periodizität der
Wellenerscheinung wird dabei durch die Wellenlänge λ der Lichtwelle charakterisiert. Wird dagegen der Verlauf an einem bestimmten Ort zu verschiedenen Zeiten betrachtet, erhält man eine Zeitraumdarstellung derselben Wellenerscheinung.
6
1.1 Wellen und Photonen
Ihre Periodizität wird dann durch die Periodendauer T oder ihren
Kehrwert, der Frequenz f gekennzeichnet.
f=
1
T
(1.2)
Ortsraumdarstellung
(1.2)
Zeitraumdarstellung
Abb. 1.2: Monochromatische Lichtwelle in Ortsraum- und Zeitraumdarstellung
Die Wellennatur des Lichtes äußert sich in zwei grundlegenden
Phänomenen: Beugung und Interferenz. Fällt beispielsweise eine
monochromatische Lichtwelle auf eine undurchsichtige Platte mit
einer kleinen runden Öffnung, so beobachtet man auf einem dahinter
liegenden Schirm eine als Beugung bezeichnete Richtungsänderung
der Lichtausbreitung an dieser Öffnung, so dass Licht auch in die
geometrische Schattenzone eindringt (1.3).
d
Abb. 1.3: Beugung und Interferenz monochromatischer Lichtwellen(Photonen) an einer runden Öffnung (Einzelspalt)
Als Beugungsbild dieser runden Öffnung sieht man auf dem undurchsichtigen Schirm eine Folge sich abwechselnder konzentrischer
dunkler und heller Ringe, deren Intensität von der Bildmitte nach
außen hin abnimmt. Dieses Beugungsmuster kommt durch Interferenz zustande. Zwei monochromatische Lichtwellen können sich an
einem bestimmten Punkt im Raum überlagern. Dabei addieren sich
sowohl ihre beiden elektrischen als auch magnetischen Feldvektoren
nach dem Superpositionsprinzip. Je nach Richtung und Betrag dieser
Feldvektoren führt die Überlagerung zu einer Verstärkung, Abschwächung oder gar Auslöschung der resultierenden Lichtwelle an
dieser Stelle. Die dadurch an bestimmten Orten entstehende Erschei-
7
1 Atomphysik
nung von hellen Lichtmaxima und dunklen Lichtminima wird Interferenz genannt.
Die mit dem Auge wahrnehmbaren Lichtwellen stellen nur einen
kleinen Ausschnitt aus dem Spektrum der elektromagnetischen
Strahlung dar (Abb. 1.4). Dem sichtbaren Bereich schließt sich zu
längeren Wellenlängen hin die Infrarot-Strahlung an, die auch als
Wärmestrahlung bezeichnet wird. Zu kürzeren Wellenlängen hin
setzt sich das elektromagnetische Spektrum über die UltraviolettStrahlung fort, dem sich die Röntgenstrahlung anschließt. Die kürzeste und energiereichste elektromagnetische Strahlung stammt aus
dem Atomkern. Sie wird als γ -Strahlung bezeichnet und begleitet
die meisten radioaktiven Zerfallsprozesse.
10
γ
20
-12
10
[eV]
10
6
Röntgen
10
UV
16
Licht
10
Fernsehen
10 8
-3
10
Mikrowellen
4
-6
Sichtbar
IR
12
10
10
10-9
UKW
Kurzwellen
Mittelwellen
Langwellen
10
0
10
4
10 0
-3
10
10-6
ioniesierend
[Hz]
nicht-oniesierend
Fr
e
W
[m]
ge
En
e
eq
u
en
z
än
nl
lle
rg
ie
Elektromagnetisches Spektrum
(Photonenstrahlung)
Längstwellen
Abb. 1.4: Elektromagnetisches Spektrum
Tritt elektromagnetische Strahlung der Frequenz f mit den Elektronen der Atome in Wechselwirkung, dann muss sie als ein materiefreier Strom von Energiequanten, den so genannten Photonen,
betrachtet werden, von denen jedes die Energie ε = h ⋅ f transportiert. Die für die Quantenphysik wichtige Naturkonstante h heißt
Plancksches Wirkungsquantum. Es ist
h = 6,626 ⋅ 10 −34 Js
8
(1.3)
1.1 Wellen und Photonen
Die atomare und subatomare Welt ist der direkten Anschauung nicht
zugänglich, denn das menschliche Gehirn ist ein Produkt der Evolution, das sich in Anpassung an die uns umgebene makroskopische
Lebenswelt optimiert hat. Daher machte Albert Einstein 1955 folgende Aussage: „Die ganzen 50 Jahre bewusster Grübelei haben
mich der Antwort der Frage „Was sind Lichtquanten“ nicht näher
gebracht. Heute glaubt zwar jeder Lump, er wisse es, aber er täuscht
sich.“
Ein wichtiges Experiment, in dem sich die Teilcheneigenschaft der
Photonen manifestiert, ist in Abbildung 1.5 dargestellt. Aus einer
Lichtquelle L treten Photonen unterschiedlicher Wellenlänge aus. Sie
fallen auf einen Monochromator (Farbfilter) M, der nur Photonen mit
einer wohldefinierten Wellenlänge durchlässt. Diese monochromatischen Photonen treffen dann auf eine Fotozelle in Form einer evakuierten Glasröhre, in der sich eine durchlässige Gitterelektrode G und
eine Fotokathode K genannte Metallplatte befinden. Dabei wird folgende Beobachtung gemacht: Wird die Fotokathode mit Licht beleuchtet, so treten aus ihr Elektronen heraus.
M
K
G
L
I
U
R
+
-
Abb. 1.5: Untersuchung des Photoeffektes
Bereits 1888 wurde dieses Phänomen durch Philipp Lenard beschrieben. Er beobachtete, dass eine elektrisch negativ geladene Metallplatte ihre elektrische Ladung verliert, wenn sie mit Licht hinreichend kurzer Wellenlänge bestrahlt wird. Diese Erscheinung wird
äußerer Photoeffekt oder lichtelektrischer Effekt genannt. Die ausgetretenen Elektronen können je nach Wahl einer elektrischen Spannung U zur Gitterelektrode gelangen und führen zu einem elektrischen Strom I. Er wird Photostrom genannt, da er durch die Photonen der einfallenden Lichtstrahlung verursacht wird. Eine derartige
Anordnung stellt eine primitive Form einer Photozelle dar, die eine
direkte Umwandlung der Strahlungsenergie des Lichtes in elektri-
9
1 Atomphysik
sche Energie ermöglicht. Die Photozelle (Solarzelle) stellt somit
einen photovoltaischen Energiewandler dar. Die Nutzung der Sonnenenergie durch Solarzellen soll in Zukunft einen wesentlichen
Beitrag zur elektrischen Energieversorgung leisten. 2014 betrug ihr
Anteil an der deutschen Bruttostromerzeugung 6,1%.
Wird bei gegebener Beleuchtungsstärke des einfallenden Lichtes die
elektrische Spannung U zwischen Photokathode und Gitterelektrode
erhöht, so steigt auch der Photostrom I an, bis alle ausgetretenen
Elektronen zur Gitterelektrode abgesaugt werden. Die dabei auftretende Sättigungsstromstärke I ist von der Beleuchtungsstärke L des
Lichtes abhängig (Abb. 1.6).
I
I1
L1
I2
L2
– U0
U
Abb. 1.6: Photostrom I in Abhängigkeit von der Beschleunigungsspannung U bei verschiedenen Beleuchtungsstärken ( L1 > L2 )
Wird eine negative elektrische Spannung U gewählt, so stößt ihr
elektrisches Feld die Photoelektronen zurück. Der Photostrom sinkt
und geht bei einer bestimmten negativen Spannung U 0 auf null
zurück. Diese Spannung wird Grenzspannung genannt. Die kinetische Energie der schnellsten Photoelektronen reicht dann nicht mehr
aus, um die Arbeit W = e ⋅ U 0 aufzubringen, die zur Überwindung
der elektrischen Abstoßung notwendig wäre. Die Photoelektronen
gelangen dann – unabhängig von der Größe der Beleuchtungsstärke
des Lichtes – nicht mehr zur Gitterelektrode.
Albert Einstein fand 1905 die Erklärung für den Photoeffekt. Licht
stellt demnach einen Strom aus endlichen im Raum lokalisierten
Energiequanten dar, „welche sich bewegen, ohne sich zu teilen und
nur als Ganze absorbiert und erzeugt werden können.“ Diese Lichtquanten oder Photonen besitzen die Energie
ε = hf =
hc
.
λ
(1.4)
Die experimentelle Beobachtung, dass Lichtwellen nur in Form von
diskreten Energiequanten, den Photonen, absorbiert werden können,
10
1.1 Wellen und Photonen
begründet das korpuskulare Verhalten von Wellen. Besitzt ein Lichtquant genügend Energie ε kann es beim Auftreffen auf ein Elektron
dieses durch Absorption über die Schwelle der Austrittsarbeit W A
heben und mit einer kinetischen Energie E kin aus dem Metallverband
freisetzen. Aufgrund der Energieerhaltung gilt dann:
ε = W A + E kin
(1.5)
E kin = ε − W A = hf − W A .
(1.6)
oder
Photonen mit einer Energie ε < W A , die kleiner als die materialspezifischen Austrittsarbeit W A der Elektronen ist, können keine Elektronen auslösen und tragen deshalb nicht zum Photostrom I bei. Die
Frequenz f der Lichtquanten muss die untere Grenzfrequenz f G für
den Photoeffekt überschreiten, um zum Photostrom beitragen zu
können.
Ekin
0
fG
f
-WA
Abb. 1.7: Kinetische Energie der Photoelektronen als Funktion von
der Lichtfrequenz
Durch Messung der Spannung U 0 kann die kinetische Energie E kin
der Photoelektronen als Funktion der Frequenz f der Lichtquanten
bestimmt werden. Für eine gegebene Metalloberfläche als Photoelektrode ergibt sich experimentell eine Gerade (Abb. 1.7), die durch
die Gleichung
E kin = eU0 = ε − W A = hf − W A
(1.7)
beschrieben wird. Aus dieser Geraden kann sowohl die Plancksche
Konstante h als auch die Austrittsarbeit W A graphisch bestimmt
werden. Der Schnittpunkt dieser Geraden mit der f-Achse liegt bei
der Grenzfrequenz f G . Durch die Grenzfrequenz wird die Lage des
11
1 Atomphysik
Schnittpunktes mit der E kin -Achse und damit die Größe der Austrittsarbeit W A festgelegt. Es gilt:
ε min = hf G = W A
fG =
WA
h
(1.8)
(1.9)
Die untere Grenzfrequenz f G besitzen die Photonen, die bei Absorption gerade die Austrittsarbeit der gebundenen Elektronen aufbringen ( E kin = 0 ). Photonen mit f > f G können diese aus dem
Metallverbund der Photokathode befreien und ihnen eine kinetische
Energie E kin > 0 übertragen.
Metall
Austrittsarbeit WA / eV
Li
2,38
Na
2,33
K
2,26
Cs
1,94
Cu
4,29
Ag
4,73
Au
5,1
Pt
5,65
Tab. 1.1: Austrittsarbeit WA für einige Metalle
Werden verschiedene Metalloberflächen bestrahlt, so erhält man
– je nach Größe ihrer Austrittsarbeit versetzte – parallele Geraden,
die alle die gleiche Steigung besitzen. Die Steigung der Geraden ist
für alle Metalle konstant; sie ist durch die Plancksche Konstante h
bestimmt.
Der Photoeffekt wird auch bei der Verstärkung schwacher Lichtsignale mit Hilfe von Sekundär-Elektronen-Vervielfachern (SEV) in
Photomultiplieren und Channel-Plates ausgenutzt; letztere werden in
Restlichtverstärkern eingesetzt.
Neben dieser Teilcheneigenschaft der Lichtwellen besitzen atomare
Teilchen auch Welleneigenschaften. Man spricht in diesem Zusammenhang von einem Welle-Teilchen-Dualismus der Materie. Eine
Vielzahl von Beugungs- und Interferenzexperimenten mit atomaren
Teilchen zeigt: Die Bewegung von materiellen Teilchen muss durch
interferenzfähige Materiewellen beschrieben werden. So demonstrierten 1927 die amerikanischen Physiker Davisson und Germer
12
1.2 Quantentheorie und Bohrsches Atommodell
Beugungsphänomene, die beim Beschuss der Kristallgitter dünner
Metallfolien mit Elektronenstrahlen auftreten. Auch Neutronenstrahlen, die aus Neutronen bestehen, besitzen Welleneigenschaften. Die
Neutronenbeugung wird in der Materialuntersuchung und bei der
Strukturaufklärung komplizierter chemischer Verbindungen eingesetzt. Dabei hängt die Wellenlänge λ dieser Materiewellen nach
einer von Louis-Victor de Broglie (1892 – 1987) angegebenen Beziehung mit dem Impuls p = m ⋅ v der Teilchen zusammen:
λ=
h
.
p
(1.10)
Der Impuls p ist eine Teilcheneigenschaft, die Wellenlänge λ eine
Eigenschaft der Wellennatur der Materie. Wellen besitzen dabei die
Eigenschaft der Nichtlokalisierbarkeit. Bei der Beschreibung von
Teilchen durch Wellen muss wegen der räumlichen Lokalisierbarkeit
des Teilchens die Ausdehnung der Welle begrenzt werden. Dies kann
durch Überlagerung von ebenen Wellen mit geringfügig verschiedenen Frequenzen geschehen. Durch eine solche Wellengruppe kann
ein Elektron dargestellt werden. Die Atomhülle der Atome besteht
aus Elektronen, über deren räumliche Verteilung nur Wahrscheinlichkeitsaussagen gemacht werden können.
1.2
Quantentheorie und Bohrsches Atommodell
Die wellenmechanische Beschreibung der Elektronen führt zur
Quantenmechanik, die im Wesentlichen von Erwin Schrödinger
(1887 – 1961) und Werner Heisenberg (1901 – 1976) formuliert
wurde. Nach Max Born (1882 – 1970) kann die ein Elektron beschreibende „Wellenfunktion“ nur statistisch interpretiert werden:
Das Quadrat ihrer Amplitude stellt ein Maß für die Wahrscheinlichkeit dar, ein Elektron in einem bestimmten Raumbereich aufzufinden. Die de Brogliesche Beziehung verbindet die Wellen- und die
Teilcheneigenschaft miteinander. Das Verbindungsglied zwischen
diesen beiden Eigenschaften ist das Plancksche Wirkungsquantum h.
Aufgrund der Kleinheit von h tritt die Wellennatur der Teilchen nicht
in der makroskopischen, sondern nur in der mikroskopischen Welt in
Erscheinung. Je leichter und je langsamer ein Teilchen ist, desto
größer ist seine Materie-Wellenlänge, und umso ausgeprägter ist
somit sein Wellencharakter.
Beispiel:
Es soll die Wellenlänge eines Elektrons ( m e = 9 ⋅ 10 −31 kg ) berechnet werden, das sich in einem H-Atom mit einer Geschwindigkeit von v = 3 ⋅ 10 8 cm / s bewegt.
13
1 Atomphysik
λ=
h
= 2 ⋅10 −8 cm
p
Damit entspricht die Materie-Wellenlänge des Elektrons etwa
dem Durchmesser des H-Atoms.
Eine technische Anwendung, die auf der Wellennatur von Elektronenstrahlen beruht, stellt das Elektronenmikroskop dar. Es besitzt ein
etwa zehntausendfach höheres Auflösungsvermögen als ein Lichtmikroskop. Das Auflösungsvermögen A wird dabei über den kleinsten noch getrennt wahrnehmbaren Abstand d zweier Punkte definiert.
Das Auflösungsvermögen wird durch Beugungseffekte der durch die
Wellenlänge λ charakterisierten Strahlung begrenzt. Die Beugungstheorie der Wellenoptik liefert für das Auflösungsvermögen die Beziehung:
A=
λ
(1.11)
d
Aufgrund der de Broglie-Beziehung
λ=
h
=
p
h
=
2 me Ekin
h
2 me eU
(1.12)
nimmt die Materie-Wellenlänge von Elektronen mit wachsender
kinetischer Energie ab. Durch die Wahl einer großen Beschleunigungsspannung U, welche die Elektronen durchlaufen, können
kleinste Strukturen mit hoher Auflösung sichtbar gemacht werden.
Das Verhalten der Materiewellen wird durch komplex-wertige Funktionen beschrieben, die sich als Lösung der Schrödinger-Gleichung,
einer partiellen Differentialgleichung von grundlegender Bedeutung
für die Atomphysik, ergeben. Aus der Quantenmechanik folgt, dass
weder Energie und Zeit noch Ort und Impuls eines bestimmten
Elektrons gleichzeitig beliebig genau gemessen werden können. Für
diese im Wellencharakter der Elementarteilchen begründeten naturgesetzlichen Beschränkungen der Messgenauigkeit gelten die 1925
von Heisenberg formulierten Unbestimmtheitsrelationen:
∆E ⋅ ∆t ≈ h
∆x ⋅ ∆p ≈ h
(1.13)
Energie E und Zeitpunkt t, an dem ein Teilchen die Energie E besitzt, können nicht gleichzeitig beliebig genau gemessen werden. Das
Produkt aus der Energieunschärfe ∆E und der Ungenauigkeit der
Zeitmessung ∆t wird durch die Plancksche Konstante h bestimmt.
Bedingt durch die Wellennatur der Materie können auch bei größtem
messtechnischem Aufwand Energie und Zeit eines Teilchens gleichzeitig nicht genauer gemessen werden. Während in der klassischen
14
1.2 Quantentheorie und Bohrsches Atommodell
Physik ein Teilchen einen im Prinzip beliebig genau messbaren Ort x
und einen beliebig genau messbaren Impuls p besitzt, besagt die
Quantenmechanik, dass bei einem sehr genau gemessenen Impuls p
(mit verschwindender Impulsunschärfe ∆p = ∆p x = 0 ) der Ort des
betrachteten Teilchens völlig unbestimmt ist ( ∆x = ∞ ) und umgekehrt.
Beispiel:
Ein sich in der Atomhülle eines H-Atoms befindliches Elektron
besitze eine kinetische Energie von
Ekin =
me
2
v2 =
p2
= 13,6 eV = 2,2 ⋅ 1018 J .
2me
Der Betrag des linearen Impulses p ergibt sich dann zu
p = 2me Ekin = 2 ⋅ 10−24 Ns .
Je nach Bewegungsrichtung kann der Impuls zwischen +p und –
p schwanken. Daraus ergibt sich dann eine Impulsunschärfe
∆p = + p − (− p ) = 2 p . Die Unbestimmtheit des Ortes (Ortsunschärfe) ∆x des Elektrons im H-Atom liegt dann gemäß der
Heisenbergschen Unschärferelation in der Größenordnung
∆x ≈
h
h
=
= 1,6 ⋅10 −10 m .
∆p 2 p
Ein Elektron im H-Atom beansprucht somit aufgrund seiner wellenmechanischen Unschärfe die gesamte Atomhülle. In der Atomphysik
kann daher die Vorstellung der klassischen Mechanik, nach der die
Elektronen auf definierten Bahnen den Atomkern umkreisen, nicht
aufrechterhalten werden. Die Elektronen bilden in der Atomhülle
vielmehr räumlich ausgedehnte Verteilungen um den Atomkern aus,
die auch als diffuse Elektronenwolken bezeichnet werden. Zur genauen Beschreibung der Elektronenzustände werden so genannte
Quantenzahlen eingeführt.
Eine einfache modellmäßige Beschreibung der Atome liefert das
Bohrsche Atommodell, das eine semiklassische Vorstufe der quantenmechanischen Beschreibung der Atome darstellt. Es basiert auf
den beiden Bohrschen Postulaten:
1. Postulat: Für das Elektron sind nur Kreisbahnen möglich, für die
der Drehimpuls des Elektrons ein Vielfaches von h = h / 2π ist; h ist
dabei das Plancksche Wirkungsquantum.
L = n h mit n = 1, 2, ...
(1.14)
15
1 Atomphysik
Auf diesen Bahnen verläuft nach Niels Bohr (1885 – 1962) das
Elektron strahlungslos. Nach der Vorstellung der Elektrodynamik
strahlt nämlich eine beschleunigte elektrische Ladung elektromagnetische Wellen ab. Das Elektron würde demnach laufend Energie verlieren und auf einer Spiralbahn allmählich in den Atomkern stürzen.
Im Rahmen der klassischen Physik ist daher die Stabilität der Atome
nicht erklärbar. Anschaulich kann das Bohrsche Atommodell wie
folgt interpretiert werden:
Im Atom sind nur solche Elektronenbahnen erlaubt, die stehenden
Wellen entsprechen. Ein typisches Beispiel für stehende Wellen liefert eine an beiden Enden eingespannte Saite.
Die Schwingungsfrequenzen dieser Saite sind quantisiert, d. h. es
sind nur solche Frequenzen möglich, die ein ganzzahliges Vielfaches
n ⋅ f1 einer Grundfrequenz f1 annehmen (Abb. 1.8).
n=1
Grundschwingung (Frequenz f1 )
n=2
1. Oberschwingung (Frequenz f2 )
n=3
2. Oberschwingung (Frequenz f3 )
Abb. 1.8: Stehende Wellen auf einer eingespannten Saite
Ein Elektron mit dem Impuls p kann sich nur dann auf einer stabilen
atomaren Bahn um den Atomkern bewegen, wenn die Bahnlänge ein
ganzzahliges Vielfaches der zugehörigen de Broglie Materiewellenlänge ist. Dabei muss der Umfang U der Kreisbahn mit dem Radius r
dem n-fachen der Materiewellenlänge λ des umlaufenden Elektrons
entsprechen.
Beispiel:
U = 2πr = nλ
r=
nλ
2π
Mit n = 4 erhält man die in Abb. 1.9 gezeigte Darstellung.
16
1.2 Quantentheorie und Bohrsches Atommodell
Für den Bahndrehimpuls L dieser Elektronenbahn erhält man dann
mit Hilfe der de Broglie-Beziehung p = h / λ :
L = r⋅ p
L=
nλ
nλ h
h
⋅p=
⋅ = n⋅
= nh
2π
2π λ
2π
(1.15)
Abb. 1.9: Stehende Elektronenwelle für n = 4
2. Postulat: Beim Übergang zwischen zwei Bahnen mit den Energien Ea und Ee wird die Energiedifferenz als Photon ausgestrahlt,
wobei für die Photonenenergie gilt:
h ⋅ f = E a − Ee .
(1.16)
–
–
Photon
–
–
–
–
–
–
–
Abb.1.10: Photonenemission infolge eines Elektronenübergangs in
der Atomhülle
17
1 Atomphysik
Es sollen nun die den stabilen Bahnen entsprechenden Energiezustände im H-Atom berechnet werden. Dazu soll die Energie E des
Elektrons ermittelt werden, das sich im Abstand r vom Atomkern
(Proton) befindet. Die Energie E setzt sich dabei als Summe aus kinetischer und potentieller Energie zusammen:
(1.17)
E = E kin + E pot
Auf das den Atomkern im Abstand r umkreisende Elektron wirken
die Coulombsche Anziehungskraft und die Zentrifugalkraft. Im
Gleichgewicht gilt:
e2
1
4πε 0 r 2
=
me v 2
(1.18)
r
Für die kinetische Elektronenenergie folgt:
Ekin =
1
1 e2
me v 2 =
2
8πε 0 r
(1.19)
Für die potentielle Energie folgt:
r
E pot = ∫ FC dr =
∞
r
∫ 4πε
∞
e2
1
0
r2
dr = −
e2
4πε 0 r
1
(1.20)
Damit erhält man für die Gesamtenergie E des Elektrons im HAtom:
E = E kin + E pot = −
e2
8πε 0 r
1
Anmerkung: Für ein einzelnes Elektron im Feld eines Atomkerns
mit Z Protonen (Element mit der Ordnungszahl Z) erhält man für die
Gesamtenergie:
E=−
1 Ze 2
8 πε 0 r
Ein Atomkern mit nur einem Elektron in der Hülle stellt ein positiv
geladenes Ion dar, welches als „wasserstoffähnliches“ Atom aufgefasst werden kann.
Das Elektron ist im H-Atom an das Proton gebunden. Dies kommt
durch das negative Vorzeichen zum Ausdruck. Ein gebundenes Teilchen besitzt immer eine negative Gesamtenergie. Durch Energiezufuhr kann das Elektron vom Atomkern getrennt werden. Im Grenzfall
18
1.2 Quantentheorie und Bohrsches Atommodell
r → ∞ erhält man für ein freies ruhendes Elektron die Gesamtenergie Null.
Im H-Atom sind nur solche Bahnen stabil, für die das 1. Bohrsche
Postulat erfüllt ist.
Die Beziehung
L=n
h
2π
stellt eine Quantisierungsbedingung für den Drehimpuls L dar. Der
Drehimpuls L kann nur ganzzahlige Vielfache von h = / 2π annehmen. Wegen L = r ⋅ p folgt:
L = n⋅h = r ⋅ p = r ⋅m⋅v
bzw.
v=
n⋅h
.
r ⋅ me
Eingesetzt in
Ekin =
1
1 e2
me v 2 =
2
8πε 0 r
ergibt:
1 n2 ⋅h2
1 e2
=
2 r2 ⋅m
8πε 0 r
e
Auflösen nach r = r (n) liefert für die Radien der stabilen Bahnen im
H-Atom:
r (n) = rn =
4πε 0h 2
me e
2
n2
(1.21)
Anmerkung: Für ein „wasserstoffähnliches“ Atom mit der Ordnungszahl Z gilt:
rn =
4πε 0 h 2
m e Ze
2
n2
Eingesetzt in die Formel für die Gesamtenergie
E=−
1 e2
8πε 0 r
ergibt schließlich: Das Elektron in einem Wasserstoffatom kann sich
nur in Zuständen mit den Energien
19
1 Atomphysik
E = E (n) = En = −
e4me
8ε 02h 2
⋅
1
n
= − RH
2
1
n
2
− = −13,6
1
n2
(eV )
(1.22)
aufhalten, wobei die sog. Hauptquantenzahl n nur die ganzzahligen
Wert n = 1, 2, ... annehmen kann. Die zugelassenen Energiezustände
des Elektrons im H-Atom hängen nur von der Hauptquantenzahl n
ab.
Für die möglichen energetischen Elektronenzustände im „wasserstoffähnlichen“ Atom mit der Ordnungszahl Z folgt:
En = −
e 4m e
8ε 02 h 2
⋅ Z2 ⋅
1
n2
= −R H
1
n2
Z 2 = −13,6
Z2
n2
(eV )
Die Konstante R H wird nach dem schwedischen Physiker Rydberg
benannt. Für die Rydberg-Konstante gilt:
RH =
e 4 me
8ε 02h 2
= 13,6 eV
(1.23)
Die atomphysikalische Einheit der Energie ist das Elektronenvolt
(Kurzzeichen: eV). Ein Elektronenvolt ist die kinetische Energie, die
ein Elektron mit der Ladung q e = e = 1,602 ⋅ 10 −19 As beim Durchlaufen einer elektrischen Potentialdifferenz (elektrischen Spannung)
von 1 Volt im Vakuum gewinnt. Die Umrechnung in SI-Einheiten
ergibt:
1 eV = 1,602 ⋅ 10 −19 As ⋅ 1V = 1,602 ⋅ 10−19Ws = 1,602 ⋅ 10 −19 J
1.2.1
(1.24)
Quantenzahlen
Das Bohrsche Atommodell kann auch auf Atome mit mehreren
Elektronen angewendet werden. Es erhebt sich die Frage, wie diese
Elektronen angeordnet sind bzw. wie man sich ihre Bewegung um
den Kern vorstellen kann.
Eine vereinfachte Antwort hierauf gibt – wie bereits erwähnt – das
Bohrsche Atommodell, eine exakte die Quantentheorie ( → Lösungen
der Schrödinger-Gleichung). Nachfolgend sollen nur die Grundvorstellungen und Ergebnisse erörtert werden. Sie führen – in Verbindung mit dem Pauli-Prinzip – zu verschiedenen Quantenzahlen, mit
deren Hilfe man die möglichen Zustände von Atomen beschreiben
und verstehen kann. Es erweist sich dabei als zweckmäßig, zunächst
immer das Wasserstoff-Atom mit – im Normalfall – nur einem Proton als Kern und einem Elektron zu diskutieren und dann zu versu-
20
1.2 Quantentheorie und Bohrsches Atommodell
chen, die gewonnenen Erkenntnisse auf die Atome anderer Elemente
zu übertragen.
Geht man vom Bohrschen Atommodel für das H-Atom aus, nach
dessen Vorstellungen ein Elektron auf einer stabilen Bahn den
Atomkern umkreist, so kommt man zu dem Ergebnis, dass vier
charakteristische Merkmale ( → Quantenzahlen) den Zustand des
Atoms im Hinblick auf sein Elektron kennzeichnen und beschreiben:
Auf jeder möglichen Bahn hat das Elektron eine bestimmte
(1) Bahnenergie ( ↔ Hauptquantenzahl n).
Das umlaufende Elektron hat aber auch einen Drehimpuls. Dieser ist
ein axialer Vektor (vgl. 1. Lerneinheit), d. h. es muss gefragt werden
nach den möglichen
(2) Beträgen des Drehimpulsvektors. Diese werden durch Einführung einer weiteren Quantenzahl charakterisiert ( ↔ Nebenquantenzahl l ).
und nach möglichen
(3) Richtungen, die der Drehimpulsvektors im Raum in Bezug
auf eine physikalisch ausgezeichnete Richtung einnehmen
kann ( ↔ Magnetquantenzahl ml). Diese Richtungsorientierung kann beispielsweise durch ein äußeres Magnetfeld
vorgegeben werden.
Außerdem hat das Elektron einen Eigendrehimpuls, auch Spin genannt, der ebenfalls ein axialer Vektor ist, bei dem aber die Betragsquantenzahl (in der Einheit h ) immer den gleichen Wert
s = + 1 2 hat, sodass nur die variablen
(4) Richtungen des Eigendrehimpulsvektors
( ↔ Spinquantenzahl ms)
zur Charakterisierung anzugeben sind.
(Grundsätzlich haben auch die Kerne Eigendrehimpulse, was z. B. in
der Kernspintomographie Anwendung findet, nicht aber bei dem o.
a. Problem zu berücksichtigen ist, bei dem es nur auf die Elektronen
ankommt und Feinheiten außer Acht gelassen werden).
Mit Hilfe der genannten Quantenzahlen können also mögliche oder
tatsächliche Energie- und Drehimpulszustände im Atom angegeben
werden. Insbesondere lässt sich eine Antwort geben auf die Fragen:
(a) Welche Zustände besetzen die Elektronen im Grundzustand
einer Atomart?
(b) Welche Übergänge in andere Zustände sind möglich bzw.
erlaubt?
Elektronen können aus der jeweils äußeren – besetzten – Bahn unter
Aufnahme (Absorption) von Energie in eine höhere – unbesetzte –
Bahn springen oder von dort unter Abgabe von Energie – im Allgemeinen durch Emission von Licht (-Quanten) – wieder zurückkeh-
21
1 Atomphysik
ren. Hier sind aber nicht alle Übergänge erlaubt, die theoretisch möglich sind: Es gelten Auswahlregeln.
1.2.1.1
Hauptquantenzahl n
Fassen wir noch einmal kurz die bisherigen Erkenntnisse zusammen:
Nach dem Bohrschen Atommodell umkreist das Elektron den Wasserstoffkern strahlungsfrei auf stabilen Bahnen. Jede dieser Bahnen
ist gekennzeichnet durch die Energie:
En = − RH ⋅
1
n
2
=−
13,6
n2
eV
(1.25)
wobei n die Hauptquantenzahl ist. Diese kann nur diskrete Werte
annehmen, und zwar alle ganzzahligen positiven Werte n = 1, 2, 3 ...,
womit auch für die einzelnen Bahnenergien diskrete Werte resultieren.
Befindet sich das einzige Elektron des H-Atoms auf der untersten
– energieärmsten – Bahn (n = 1), so spricht man vom Grundzustand,
auf einer höheren Bahn vom angeregten Zustand des Atoms.
Bei Zufuhr von Energie kann das Elektron auf eine höhere Bahn
„springen“, bei Entzug von dort – unter Abgabe der Energie in Form
von Photonen – auf eine niedrigere Bahn „zurückspringen“. Erlaubt
sind nach der Auswahlregel alle ganzzahligen Übergänge, also
∆n = ±1, ±2, ±3 ... .
Obwohl das Bohrsche Atommodell erfolgreich das Spektrum des
Wasserstoffatoms erklären konnte, musste es korrigiert bzw. durch
Erkenntnisse aus der Quantentheorie ersetzt werden, da es vor allem
auch bei Atomen mit mehreren Elektronen versagt. So widerspricht
die Existenz diskreter Umlaufbahnen der Heisenbergschen Unschärfe-Relation. Deshalb setzt man bei Atomen mit zwei und mehr Elektronen das Bahn- durch das Schalenmodell der Atomhülle, ausgehend
von folgenden Fakten:
1.
22
Die im Atom energetisch möglichen und erlaubten Zustände
können von mehreren Elektronen besetzt und zu Gruppen
mit ähnlicher Gesamtenergie, die man dann als Schalen bezeichnet, zusammengefasst werden. Diese Schalen kennzeichnet man mit großen lateinischen Buchstaben, wobei
folgende Beziehung zwischen ihnen und den Hauptquantenzahlen n besteht:
n = 1 2 3 4 ...
K L M N ...-Schale
1.2 Quantentheorie und Bohrsches Atommodell
2.
Jede Schale bietet nur einer ganz bestimmten Zahl von
Elektronen Platz. Auf einer Schale mit der Hauptquantenzahl n können maximal 2n2 Elektronen untergebracht werden, d. h. die maximale Aufnahmekapazität an Elektronen
beträgt bei der K-Schale 2 ⋅ 12 = 2 , bei der L-Schale
2 ⋅ 2 2 = 8 und bei der M-Schale 2 ⋅ 3 2 = 18 .
Die einzelnen Schalen bestehen noch aus „Unterschalen“, wie im
nachfolgenden Kapitel 1.2.1.2 näher ausgeführt wird.
Anmerkung: Statt einer diskreten Elektronenbahn liefert die jeweilige Lösung der Schrödinger-Gleichung eine Wellenfunktion. Diese
kann man einigermaßen anschaulich darstellen als räumlichen Bereich, in dem sich das entsprechende Elektron mit maximaler Wahrscheinlichkeit aufhält. Statt Wellenfunktion bzw. wahrscheinlichem
Aufenthaltsbereich verwendet man im Allgemeinen den Begriff
(Atom-) Orbital.
1.2.1.2
Nebenquantenzahl l
r
Die möglichen Bahn-Drehimpulse L des Elektrons können folgende
Beträge annehmen:
L = l(l + 1)h
(1.26)
Hierbei ist l die Nebenquantenzahl oder auch (Bahn-) Drehimpulsquantenzahl. Sie kann nach den Regeln der Quantenmechanik
die folgenden Werte haben:
l = 0, 1, 2, ..., n – 1
(1.27)
d. h. die Nebenquantenzahl ist ganzzahlig, positiv und kann jeweils
genau n Werte annehmen. Dementsprechend gilt:
n=1 → l =0
n = 2 → l = 0 oder 1
n = 3 → l = 0 oder 1 oder 2.
Die Auswahlregel fordert hier: ∆l = ±1.
Die Drehimpulsquantenzahl l = 0 entspricht klassisch der Kreisbahn
des Elektrons. Die anderen Drehimpulsquantenzahlen beschreiben
im Rahmen einer mechanischen Interpretation die Exzentrizität von
Ellipsenbahnen. Das H-Atom ist bezüglich der Drehimpulsquantenzahl l energetisch entartet, d.h. es besitzt für beliebige l -Werte die
gleiche Energie E n . Die Atome aller anderen Elemente sind nicht
entartet, d. h. bei gegebenen n-Werten nimmt die Energie ihrer Elekt-
23
1 Atomphysik
ronen mit wachsender Drehimpulsquantenzahl l zu. Zu festen Werten von n und l sind mehrere Zustände mit gleicher Energie E n,l
erlaubt.
Elektronen einer Schale mit gleicher Nebenquantenzahl bilden eine
Unterschale. In der Chemie ist es üblich, diese Unterschalen mit
kleinen lateinischen Buchstaben zu kennzeichnen, wobei folgende
Zuordnung besteht:
l =0
s
1
p
2
d
3
f
...
...-Unterschale
Haupt- und zugehörige Unterschalen sind in Abb. 1.11 schematisch
dargestellt.
3d
M
n=3
3p
3s
L
n=2
2p
2s
K
n=1
1s
Abb. 1.11: Schematische Darstellung der energetischen Struktur der
Atomhülle in Form von Haupt- und Unterschalen
Die hier willkürlich erscheinende Quantisierung des Drehimpulses in
diskrete l -Werte ergibt sich mathematisch zwangsläufig aus der
Lösung der Schrödinger-Gleichung, der grundlegenden Wellengleichung der Quantenmechanik. Diese besitzt nur für diskrete Eigenwerte l des Drehimpulses eindeutige und endliche Lösungen.
1.2.1.3
Magnetquantenzahl ml
Die möglichen Richtungen, in welche die Achse der Drehbewegung
des Elektrons um den Atomkern und damit sein Drehimpulsvektor
zeigen kann, ist durch die Magnetquantenzahl ml festgelegt. Sie kann
nur die folgenden diskreten Werte annehmen:
ml = – l , – l + 1, ..., –1, 0, 1, ... l – 1, l
insgesamt also 2 l + 1 Werte. Dementsprechend gilt:
24
(1.28)
1.2 Quantentheorie und Bohrsches Atommodell
l = 0 → ml = 0
l = 1 → ml = –1 oder 0 oder +1
l = 2 → ml = –2 oder –1 oder 0 oder +1 oder +2 ...
Der Name Magnetquantenzahl ist dadurch zu erklären, dass der
Übergang von einer Ausrichtung des axialen Bahndrehimpulsvektors
in eine andere räumliche Lage die Zu- oder Abfuhr von Energie erfordert. Die Zufuhr lässt sich z. B. mit Hilfe eines Magnetfeldes erreichen, dessen Richtung man im Allgemeinen mit der Raumkoordinate z verbindet (Abb. 1.12). Es gilt dann für den Betrag, den die
Komponente des Drehimpulses in z-Richtung hat:
(1.29)
L z = ml ⋅ h
B
z
3
m =2
L
l
1
0
–1
–2
–3
Abb. 1.12: Richtungsquantisierung des Drehimpulses
Entdeckt wurde dieser Effekt von dem niederländischen Physiker
Pieter Zeeman. Er beobachtete 1896 in Spektren von Atomen, die
einem äußeren Magnetfeld ausgesetzt waren, eine Aufspaltung der
Spektrallinien in mehrere Einzellinien. Diese Erscheinung wird daher als Zeeman-Effekt bezeichnet.
25
1 Atomphysik
1.2.1.4
Spinquantenzahl ms
Der mögliche Eigendrehimpuls eines Elektrons hat folgenden Betrag:
Ls = s ( s + 1)h
(1.30)
wobei s die (Betrags-) Spinquantenzahl ist. Sie hat nur den einen
Wert:
1
s=+
(1.31)
2
sodass auch für Ls nur ein Wert resultiert. Da s also konstant ist, führt
man sie nicht eigens als Quantenzahl auf.
Die möglichen Richtungen, in welche die Achse der Eigendrehbewegung des Elektrons und damit sein Eigen-Drehimpulsvektor
zeigen kann, gibt die (magnetische Richtungs-) Spinquantenzahl ms
an. Sie kann – in Analogie zur Magnetquantenzahl ml – insgesamt
2s + 1 diskrete, d. h. für das einzelne Elektron die zwei Werte annehmen:
m s = + 1 2 und m s = − 1 2
(1.32)
Anmerkung
1) Zwischen s und ms wird häufig nicht scharf unterschieden:
Es wird nur von „Spinquantenzahl“ gesprochen, da für s und ms
der Betrag gleichermaßen ½ ist. Zur Beschreibung der räumlichen Orientierung des Elektronenspins muss aber die (variable)
Quantenzahl ms angegeben werden, die aus Wert und
Vorzeichen besteht.
2) Man darf die – für das einzelne Elektron konstante –
Quantenzahl s nicht verwechseln mit dem Symbol s, das für die
Unterschale mit der Nebenquantenzahl l = 0 verwendet wird
Die Ausführungen über die Spinquantenzahl gehen zurück auf eine
Entdeckung der Physiker Otto Stern und Walter Gerlach. Sie beobachteten 1922 bei Messungen der atomaren magnetischen Momente
in Atomstrahlexperimenten, dass sich ein Strahlenbündel von neutralen Ag-Atomen im Grundzustand mit einem äußeren 5s-Elektron
(n = 5, l = 0, kurz auch als 5s-Zustand bezeichnet), im inhomogenen Magnetfeld in zwei Strahlenbündel (1) aufteilt (Abb. 1.13). Die
Silberatome besitzen wegen ihrer Elektronenstruktur der Atomhülle
das gleiche magnetische Moment wie ein einzelnes Elektron. Nach
klassischer Vorstellung hatte man eine kontinuierliche Verteilung der
Ag-Atome erwartet (2).
26
1.2 Quantentheorie und Bohrsches Atommodell
(1)
N
Atomstrahl
(2)
S
Abb. 1.13: Stern-Gerlach-Versuch in schematischer Darstellung
Das magnetische Moment der Atome, das mit der Bahnbewegung
des Elektrons verbunden ist, ist dem Bahndrehimpuls proportional.
Im 5s-Zustand ist der Bahndrehimpuls des Elektrons jedoch Null,
weshalb das magnetische Moment des Ag-Atoms in diesem Zustand
ebenfalls Null ist und folglich das Magnetfeld keine Wirkung auf die
Bewegung der Silberatome haben sollte. Des Weiteren zeigten spektroskopische Untersuchungen mit hoher Auflösung, dass die Spektrallinien des Wasserstoffatoms eine Feinstruktur in Form von Doppellinien (Dublettes) aufwiesen, die auch bei Abwesenheit eines Magnetfeldes auftraten. Diese Beobachtungen wiesen auf einen noch
nicht erfassten Parameter hin. Zur Erklärung dieser Untersuchungsergebnisse nahmen 1925 die amerikanischen Physiker G. Uhlenbeck
und S. Goudsmith an, dass das Elektron über einen Eigendrehimpuls
verfügt, der nicht mit der Bewegung des Elektrons im Raum verbunden ist und der als Spin bezeichnet wurde. Der Spin des Elektrons
stellt wie die Ladung und Masse eine intrinsische Eigenschaft des
r
Elektrons dar. Der mit dem Spin verbundene Eigendrehimpuls LS
ist die Ursache dafür, dass das Elektron als Elementarteilchen ein
magnetisches Moment besitzt
r
Der Vektor LS des Elektronspins kann nur solche Orientierungen im
Raum annehmen, bei denen seine Projektion L S , z auf eine willkürlich festgelegte Richtung eines äußeren Magnetfeldes (historisch
wird diese als z-Richtung bezeichnet) diskrete Werte m s besitzt, die
ein Vielfaches von h sind. Es gilt:
LS , z = m s h
(1.33)
Durch die beiden Werte der magnetischen Spinquantenzahl ms verdoppelt sich die Anzahl der unterschiedlichen Zustände, die von
Elektronen mit derselben Hauptquantenzahl n besetzt werden können. Insgesamt lassen sich in einer Schale mit der Hauptquantenzahl
n maximal
n−1
2 ∑ (2l + 1) = 2n 2
(1.34)
l =0
27
1 Atomphysik
Elektronen unterbringen, die sich auf n Unterschalen verteilen.
Zusammenfassend sei noch einmal festgestellt: Für die vollständige
Beschreibung des Zustands eines Elektrons im Atom sind vier Quantenzahlen erforderlich: Haupt-, Bahndrehimpuls-, Magnet- und
(magnetische) Spinquantenzahl. Um Übereinstimmung mit sämtlichen experimentellen Befunden zu erzielen, formulierte 1925 Wolfgang Pauli ein Ausschließungsprinzip, heute kurz als PauliPrinzip bezeichnet:
„Es kann niemals zwei oder mehrere äquivalente Elektronen im Atom geben, für welche die Werte aller Quantenzahlen (n, l , ml, ms) übereinstimmen. Ist ein Elektron im Atom vorhanden, für das diese Quantenzahlen
bestimmte Werte haben, so ist dieser Zustand „besetzt“. Zu jedem Satz dieser vier Quantenzahlen gibt es
in einem Atom höchstens ein Elektron.“
Das Ausschließungsprinzip ist mit dem Spin des Elektrons verknüpft, der anschaulich mit der Vorstellung eines rotierenden Elektrons, analog eines um eine eigene Achse rotierenden Kreisels, in
Zusammenhang gebracht werden kann. Das Pauli-Prinzip beschränkt
dabei die Höchstbesetzungszahl pro Zustand auf eins. Der Spin der
Elektronen bildet eine unveränderliche Größe, die stets den gleichen,
festen Wert hat. Aus den oben genannten historischen Gründen besitzt der Spin des Elektrons den Wert 1/2 h . Es handelt sich dabei um
die kleinste und nicht weiter teilbare Größe, in der Drehimpulse in
der Natur vorkommen. Träger dieser Drehimpulse sind Elementarteilchen, die als Fermionen bezeichnet werden. Zu dieser Gruppe
gehören auch die Protonen und Neutronen.
1.2.2
Atombau und das Periodensystem der Elemente
Die unübersichtliche Fülle der uns umgebenden Substanzen lässt
sich chemisch auf wenige Grundstoffe, die chemischen Elemente,
zurückführen. 1869 ordneten Dmitrij Mendelejew (1834 – 1907) und
Lothar Meyer (1830 - 1895) unabhängig voneinander die Gesamtheit
der chemischen Elemente mit zunehmender relativer Atommasse zu
einem periodischen System.
Die chemischen Elemente werden im periodischen System so angeordnet, dass Elemente mit ähnlichen chemischen und physikalischen
Eigenschaften untereinander in senkrechten Spalten, den so genannten Gruppen, zusammengefasst werden. Dadurch ergeben sich unterschiedlich lange waagrechte Reihen, die so genannten Perioden, bis
zum erneuten Auftreten von Elementen mit entsprechendem Verhalten (Abb. 1.14). Noch vor der Entdeckung des Elektrons, die erst
1897 durch Joseph John Thomson (1856 – 1940) erfolgte, deuteten
28
1.2 Quantentheorie und Bohrsches Atommodell
die Regelmäßigkeiten des Periodensystems auf eine innere Struktur
der Atome hin.
Erst 1913 erkannte der englische Physiker Henry Moseley (1887 –
1915), dass nicht die Atommasse, sondern die Kernladungszahl Z die
richtige Reihenfolge der Elemente im Periodensystem bestimmt. Die
Elemente werden dabei entsprechend ihrer Reihenfolge mit Ordnungszahlen Z durchnumeriert, durch die ihr Platz im periodischen
System charakterisiert wird. Die Ordnungszahl ist identisch mit der
Anzahl der Elektronen in der Atomhülle und entspricht wegen der
elektrischen Neutralität der Atome ihrer Kernladungszahl.
Abb. 1.14: Hauptgruppenelemente des Periodensystems
Erst mit Hilfe des Pauli-Prinzips, das eine Begrenzung der Besetzungszahlen der Elektronenzustände in den Atomen postuliert, konnte die Periodizität der Eigenschaften der chemischen Elemente infolge der schalenartigen Elektronenstruktur der Atomhüllen erklärt
werden. Ein vollständiges Periodensystem der Elemente (Version:
2007) der International Union of Pure and Applied Chemistry (IUPAC) ist im Anhang 3 dargestellt.
Die Elemente der ersten Periode, Wasserstoff und Helium, besitzen
eine einzige Elektronenschale. Das Wasserstoffatom hat nur ein
Elektron, das sich im 1s-Zustand befindet. Dieser Zustand wird
durch die Quantenzahlen n = 1, l = 0, ml = 0 und – da die Orientierung des Spins beliebig ist –, entweder m s = +1 / 2 oder m s = −1 / 2
gekennzeichnet. Nach dem Aufbauprinzip entsteht jedes Element aus
dem vorausgegangenen durch Hinzufügen sowohl eines Protons zum
Atomkern als auch eines Elektrons zur Atomhülle. Damit kommt
man zum Heliumatom, dessen beide Elektronen sich im 1s-Zustand
befinden, jedoch wegen des Paulischen Ausschließungsprinzips mit
antiparallelen Spinorientierungen. Seine Elektronenkonfiguration hat
29
1 Atomphysik
in symbolischer Schreibweise die Form 1s 2 . Die Besetzung der KSchale ist damit abgeschlossen. Mit dem nächsten Element, dem
Lithium, beginnt die 2. Periode des Periodensystems der Elemente.
Die Elemente der zweiten Periode besitzen zwei Elektronenschalen.
Das dritte Elektron des Lithiumatoms (Z = 3) wird in den energetisch
tiefstgelegenen Zustand der L-Schale mit n = 2 eingebaut. Dieser
wird als 2s-Zustand bezeichnet. Die Elektronenkonfiguration des LiAtoms lautet damit: 1s 2 2 s . Das nächste Element ist Beryllium. Es
besitzt 4 Elektronen. Nach dem Aufbauprinzip wird das vierte Elektron in die 2s-Unterschale eingebaut, womit diese vollständig besetzt
ist. Die Elektronenkonfiguration des Be-Atoms lautet: 1s 2 2 s 2 . Die
L-Schale mit n = 2 besitzt zwei Unterschalen mit
l = 0 (2s-Unterschale mit der maximalen Besetzungszahl 2)
und
l = 1 (2p-Unterschale mit der maximalen Besetzungszahl 6).
Durch sukzessives Auffüllen der 2p-Unterschale mit Elektronen
erhält man für die nächsten Elemente folgende Elektronenkonfigurationen:
Bor (Z = 5):
Kohlenstoff (Z = 6):
Stickstoff (Z = 7):
Sauerstoff (Z = 8):
Fluor (Z = 9):
Neon (Z = 10):
1s 2 2 s 2 2 p
1s 2 2 s 2 2 p 2
1s 2 2s 2 2 p 3
1s 2 2 s 2 2 p 4
1s 2 2s 2 2 p 5
1s 2 2 s 2 2 p 6
Die 2. Periode des Periodensystems endet mit der vollständigen Besetzung der 2p-Unterschale mit dem Edelgas Neon. Allgemein gelten
folgende Gesetzmäßigkeiten beim Aufbau des Periodensystems:
–
Die Periodenummer eines Elements gibt an, welches die
äußerste Hauptschale ist, auf der sich Elektronen befinden.
–
Aus der Zugehörigkeit eines Elementes zu einer Hauptgruppe
ergibt sich die Anzahl der Elektronen auf der äußersten Hauptschale. Diese werden Außen- oder Valenzelektronen genannt.
–
Das chemische Verhalten eines Elements wird bestimmt durch
die Anzahl der Elektronen auf der äußersten Elektronenschale.
Daher verhalten sich Elemente der gleichen Hauptgruppe chemisch ähnlich.
Aus energetischen Gründen sind Atome, bei denen die äußerste sund p-Unterschalen vollständig besetzt sind und bei denen sich noch
keine Elektronen auf den nächst höheren Schalen befinden, besonders stabil. Diese Atome gehören zur 8. Hauptgruppe und bilden die
Gruppe der Edelgase. Mit Ausnahme des Heliums besitzen alle
30
1.2 Quantentheorie und Bohrsches Atommodell
Edelgase ein Oktett von acht Außenelektronen. Edelgasatome sind
aufgrund ihrer stabilen Edelgaskonfiguration chemisch ausgesprochen reaktionsträge, d. h. sie nehmen i. a. nicht an chemischen Reaktionen teil. Diese besondere Stabilität kommt auch in ihren hohen
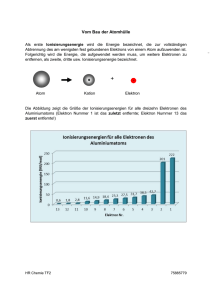
Ionisierungsenergien zum Ausdruck (Abb. 1.15).
Abb. 1.15: Ionisierungsenergie als Funktion der Ordnungszahl
Auf die reaktionsträgen Edelgase Helium (He), Neon (Ne), Krypton
(Kr) und Xenon (Xe) folgen unmittelbar die chemisch reaktionsfreudigen Alkali-Elemente Lithium (Li), Natrium (Na), Kalium (K),
Rubidium (Rb) und Caesium (Cs). Sie stehen in der I. Hauptgruppe
untereinander und weisen alle ähnliche Eigenschaften auf, beispielsweise geringe Dichten ρ und niedrige Schmelztemperaturen ϑ S
(Tab. 1.2). Gleichzeitig besitzen sie die geringsten Ionisierungsenergien aller Atome des periodischen Systems der Elemente.
Li
Na
K
Rb
Cs
Z
3
11
19
37
55
ϑ S / °C
179,00
97,8
63,5
39,0
28,5
ρ /( g / cm3 )
0,53
0,97
0,85
1,52
1,88
Tab. 1.2: Eigenschaften der Elemente der I. Hauptgruppe
(Alkalimetalle)
Offenbar lassen sich Elektronen leichter aus kaum gefüllten als aus
vollständig besetzten Schalen entfernen. Die Elektronen der Atomhülle müssen in ständiger Bewegung bleiben, damit sie nicht infolge
der elektrischen Anziehungskräfte in den Atomkern stürzen. Sie
besitzen daher sowohl kinetische als auch potentielle Energie. Die
potentielle Energie ist umso größer, je weiter vom Atomkern sich ein
Elektron im Mittel aufhält, denn zur Entfernung eines Elektrons vom
Atomkern muss Arbeit gegen die Coulombsche Anziehungskraft
31
1 Atomphysik
verrichtet werden. Um ein Elektron vollständig von einem Atom
abzutrennen, ist eine Mindestenergie notwendig, nämlich die Ionisierungsenergie. Diese Ionisierungsenergie als Funktion der Ordnungszahl spiegelt die Periodizität einer physikalischen Eigenschaft der
Elemente wider.
Diese Periodizität äußert sich auch in der Systematik der Atomradien, die in Abb. 1.16 als Funktion der Ordnungszahl Z dargestellt
sind.
Fr
3,5
Atomradien RA / 10-10m
Cs
Rb
3
K
Li
2,5
Eu
Na
Yb
2
H
1,5
Ru
Cl
At
U
Br
F
0
20
40
80
60
Ordnungszahl Z
Abb. 1.16: Atomradien für Elemente mit Z < 21
In Abbildung 1.16 sind die berechneten Radien der neutralen Atome
in Abhängigkeit von der Ordnungszahl Z aufgetragen. Zu ihrer Berechnung wurden bei festen und flüssigen Elementen die jeweiligen
Dichten bei 20°C zugrunde gelegt. Bei den gasförmigen Elementen
wurden die Dichten ihrer flüssigen Phase unterhalb des Siedepunktes
verwendet. Für ein Element mit dem Volumen V, der Masse m und
N
gilt:
der Stoffmenge n =
NA
N
⋅M
m n ⋅ M NA
ρ= =
=
V
V
V
32
(1.35)
100
1.2 Quantentheorie und Bohrsches Atommodell
Das Atom-Volumen, das von einem Atom in Anspruch genommen
wird sei
VA =
4π 3
RA .
3
Da das kugelförmige Atomvolumen nicht den ganzen Raum lückenlos ausfüllt gilt:
V
≠ VA
N
Mithilfe der Raumerfüllung RE folgt:
RE ⋅
V
= VA
N
VA =
M ⋅ RE
NA ⋅ ρ
.
Damit erhält man zur Berechnung der Atomradien die Beziehung:
RA =
3M ⋅ RE
4π ⋅ ρ ⋅ NA
(1.36)
Die dichteste Kugelpackung besitzt eine maximale Raumerfüllung
M
von RE = 0,74. Mit der Atommasse m A =
erhält man schließlich
NA
folgende Berechnungsformel für den Atomradius:
R A = 0,56 ⋅ 3
mA
ρ
(1.37)
Die Alkaliatome, mit denen jeweils die Besetzung einer neuen Elektronenschale beginnt, besitzen in Bezug auf ihre Nachbarelemente die
größten Atomradien. Die auf abgeschlossenen inneren Schalen befindlichen Elektronen sind fest gebunden und bilden einen positiv
geladenen Atomrumpf, der quasi von einem äußeren „Leuchtelektron“ als einfach positive Punktladung gesehen wird. Die inneren
(Z – 1) Elektronen kompensieren gerade (Z – 1) positive Ladungen
der Protonen im Atomkern. Infolge dieser elektrischen Abschirmung
ist das Leuchtelektron schwach gebunden und kann sich daher im
großen Abstand vom Atomkern bewegen. Innerhalb einer Hauptgruppe nehmen die Atomradien mit wachsender Ordnungszahl Z zu,
da mit jeder neuen Periode jeweils eine neue, weiter außen gelegene
Elektronenschale dazukommt. Innerhalb einer Periode dagegen werden die Atomradien mit wachsender Ordnungszahl Z kleiner. Obwohl die Atome der Elemente einer Periode die gleiche Anzahl von
Elektronenschalen besitzen, wächst mit zunehmender Kernladung
die Coulombsche Anziehungskraft auf die gleich bleibende Anzahl
33
1 Atomphysik
von Elektronen in den inneren Schalen. Gleichzeitig nimmt die Abschirmwirkung des Atomrumpfes auf die Außenelektronen ab und
verkleinert dadurch den Atomradius. Dementsprechend besitzen
innerhalb der Elemente einer Periode die Halogenatome Fluor,
Chlor, Jod und Brom mit jeweils 7 Außenelektronen die kleinsten
Atomradien.
Aus energetischen Gründen wird, wenn die p-Unterschale einer
Hauptschale gefüllt ist, als nächstes die s-Unterschale der nächst
höheren Hauptschale besetzt. Nach dem Auffüllen einer pUnterschale wird daher eine neue Periode des Periodensystems begonnen. Erst bei höheren Ordnungszahlen werden dann die noch
freien d- und f-Unterschalen der weiter innen liegenden Hauptschalen schrittweise besetzt.
1.3
Atomspektren: Strahlungsabsorption und -emission
Atome absorbieren und emittieren Lichtquanten durch elektronische
Übergänge in der Atomhülle. Durch Absorption eines Photons der
Frequenz f kann ein Atom vom Grundzustand (Energie Eg) in einen
angeregten Zustand (Energie Ea) übergehen, wenn die Bedingung
hf = Ea – Eg erfüllt ist. Im Allgemeinen gehen angeregte Atome nach
einer mittleren Lebensdauer von etwa 10–8 s unter Aussendung elektromagnetischer Strahlung in Form von Photonen wieder in den
Grundzustand über. Der Grundzustand ist der stabilste Zustand im
Atom. Er besitzt die niedrigste Gesamtenergie. Alle anderen Zustände werden als angeregte Zustände bezeichnet, da es einer Energiezufuhr von außen bedarf, um ein Elektron auf diese Zustände anzuheben. Beträgt der Energieunterschied zwischen den beiden an der
Emission beteiligten Zuständen ∆E , dann gilt für die Frequenz f der
emittierten Photonen:
f =
∆E E a − E g
=
.
h
h
(1.38)
Die Lichtquanten der Frequenz f enthalten die kleinste für diese bestimmte Frequenz erzeugbare und nachweisbare Strahlungsenergie.
Sie ist keine kontinuierlich veränderbare Größe, sondern quantisiert.
(gequantelt). Beim Übergang eines Elektrons in der Atomhülle von
einer „Bahn“ zu einer anderen wird genau ein Photon absorbiert oder
emittiert.
Unter dem Spektrum einer Strahlungsquelle versteht man eine Darstellung, in der die Intensität der emittierten Strahlung als Funktion
der Frequenz oder der Wellenlänge aufgetragen ist. Die Spektren von
Atomen sind diskrete Linienspektren. Die experimentelle Aufnahme
von Spektren wird als Spektralanalyse bezeichnet. Jedes chemische
Element ist im gasförmigen Zustand durch sein Spektrum eindeutig
charakterisiert. Prinzipiell unterscheidet man zwischen Emissions-
34
1.3 Atomspektren: Strahlungsabsorption und -emission
und Absorptionsspektren. Die Spektren werden umso komplizierter,
je mehr Atome sich zu Molekülen zusammenlagern oder sich im
engen Verband von Flüssigkeiten oder Festkörpern befinden und
dementsprechend durch Wechselwirkungskräfte sich gegenseitig
beeinflussen. Die Anzahl der Energieniveaus der Elektronen nimmt
dadurch in kondensierter Materie stark zu. Erhitzte feste oder flüssige Stoffe (z. B. Metallschmelzen) emittieren im Gegensatz zu den
Linienspektren einzelner Atome ein breites kontinuierliches Spektrum.
Abb. 1.17: Emissionsspektrum
Untersucht man die Strahlung, die von angeregten Atomen ausgeht,
dann registriert man ein Emissionsspektrum in Form von leuchtenden Linien auf dunklem Grund (Abb. 1.17). Es spielt dabei keine
Rolle, wie die Atome angeregt wurden.
Die Emissionsspektren der Atome wären äußerst linienreich und
damit unübersichtlich, wenn alle Übergänge zwischen beliebigen
Energieniveaus erlaubt wären. Das emittierte Photon führt aber einen
Eigendrehimpuls, nämlich den Spin s = 1 h mit sich, sodass zur Erfüllung des Drehimpulserhaltungssatzes der Drehimpuls des Atoms sich
bei Emission eines Lichtquants um eine Einheit ändern muss. Für
alle Atome sind nur die Strahlungsübergänge erlaubt, bei denen zwischen angeregten Zustand ( E a , l a ) und Endzustand ( E e , l e ) die
Auswahlregel
l a − l e = ∆l = ±1
(1.39)
erfüllt ist. Die Erhaltungssätze der Physik schränken somit die Vielfalt der denkbaren Vorgänge ein. Es sind nur die Strahlungsübergänge in einem Atom erlaubt und damit experimentell beobachtbar, die
in Übereinstimmung mit den Erhaltungssätzen stehen.
35
1 Atomphysik
Wird dagegen eine Substanz S mit kontinuierlichem Licht bestrahlt,
das alle Frequenzen eines bestimmten Bereichs enthält, dann registriert man im Spektrum der durchgehenden Strahlung fehlende Frequenzen, die im Absorptionsspektrum (Abb. 1.18) als dunkle Absorptionslinien vor einem hellen Hintergrund erscheinen.
Meßanordnung: Absorptions-Spektroskopie
Probe
PhotonenDetektor
Datenaufzeichnung
Lichtquelle
Meßergebnis: Absorptionsspektrum
Intensität
Wellenlänge
Abb. 1.18: Absorptionsspektrum
Beispiel: H-Atom
Das Wasserstoffatom ist das einfachste Atom. Es besitzt nur ein
Elektron in seiner Atomhülle. Bei Strahlungsabsorption kann
das Elektron aus dem Grundzustand (n = 1) in einen der angeregten Zustände (n = 2, 3, ...) übergehen. Nur Frequenzen, die
diesen Energien entsprechen, werden im Absorptionsspektrum
fehlen. Das Absorptionsspektrum von Wasserstoff wurde bereits
1814 von Joseph von Fraunhofer (1787 – 1826) bei der spektralen Untersuchung des Sonnenlichtes beobachtet. Die von der
Sonnenoberfläche ausgesandte elektromagnetische Strahlung
wird teilweise von der die Sonne umgebende Wasserstoffatmosphäre absorbiert. Die absorbierten Frequenzen werden auf
der Erde als dunkle Linien, den so genannten FraunhoferLinien, im Spektrum der Sonnenstrahlung beobachtet.
Bei der Strahlungsemission werden die emittierten Frequenzen
als helle Linien registriert. Alle Übergänge, denen das unterste
Energieniveau gemeinsam ist, gehören im Emissionsspektrum
zur gleichen Serie. Jede Serie wird durch einen eigenen Namen
gekennzeichnet.
Lyman-Serie:
Balmer-Serie:
36
unterstes Niveau → n = 1.
unterstes Niveau → n = 2.
1.3 Atomspektren: Strahlungsabsorption und -emission
Paschen-Serie:
unterstes Niveau → n = 3.
Die im H-Atom möglichen Elektronenübergänge sind in Abb. 1.19
als Pfeile dargestellt. Pfeile die auf derselben Elektronenbahn enden,
gehören zu einer Serie von Übergängen.
Für den Übergang eines Elektrons im H-Atom aus der m-ten Bahn
mit der Gesamtenergie E m in die n-te Bahn (m > n) mit der Gesamtenergie E n gilt:
∆E = hf = E m − E n = − R H (
1
m
2
−
1
n2
)
(1.40)
Für die Balmer-Serie ist n = 2, und man erhält für m = 3 die H α Linie, für m = 4 die H β -Linie, für m = 5 die H γ -Linie usw.
37
1 Atomphysik
Balmer-Serie des H-Atoms
n=3
n=4
H
H
a
H
b
rot
n=5 n=6
g
H
d
blau-grün blau violett
650
600
550
500
450
400
350
λ in mm
H
d
BalmerSerie
H
PaschenSerie
g
H
b
H
a
LymanSerie
1
2
Atomkern
3
4
n
Abb. 1.19: Emissionsspektrum des Wasserstoffatoms
1.4
Laser
Elektronen befinden sich in Atomen stets in Quantenzuständen mit
diskreten Energiewerten. Im Folgenden soll vereinfachend ein Atom
mit nur zwei Zuständen mit den Energie E1 und E 2 betrachtet werden. Befindet sich ein Atom im Grundzustand (A bzw. 1), so kann es
durch Absorption eines Photons geeigneter Energie ∆E = h ⋅ f12 in
den angeregten Zustand (A* bzw. 2) übergehen (Abb. 1.20).
38
1.4 Laser
Vorher
Nachher
Photon
E2
(2)
∆E = hf
∆E = hf
1 2
1 2
E1
(1)
e
A
A*
Abb. 1.20: Absorption eines Photons
Nach einer kurzen Zeitspanne, der Lebensdauer ( ∆t ≈ 10 −8 s ) des
Zustandes, kann das angeregte Atom A* spontan, ohne irgendeine
äußere Einwirkung durch Emission eines Photons der Energie
∆E = E 2 − E1 = h ⋅ f12 wieder in den ursprünglichen Grundzustand
übergehen (Abb. 1.21).
Vorher
Nachher
E2
e
Photon
(2)
∆E = hf
∆E = hf
1 2
1 2
E1
(1)
A*
A
Abb. 1.21: Spontane Emission eines Photons
Befinden sich mehrere Atome im angeregten Zustand (2), so sind die
spontanen Emissionen unabhängig voneinander, und die in Form von
Photonen dabei abgegebene elektromagnetische Strahlung ist nicht
kohärent.
Wirkt dagegen auf ein Atom im angeregten Zustand (2) von außen
elektromagnetische Strahlung in Form eines Photons der Energie
∆E = E 2 − E1 = h ⋅ f12 ein, so kann ein erzwungener Übergang in
den Grundzustand (1) erfolgen, wobei ein Photon derselben Energie
emittiert wird (Abb. 1.22).
Dieser Vorgang, der bereits 1916 von Einstein postuliert wurde, wird
induzierte Emission genannt. Dabei sind die durch einen induzierten
Elektronenübergang hervorgerufenen sekundären Photonen identisch
mit den primären Photonen, die den Emissionsvorgang erzwungen
haben.
39
1 Atomphysik
Vorher
Nachher
E2
P h o to n
∆E = h f
e
P h o to n
∆E = h f
(2)
1 2
P h o to n
∆E = h f
∆E = hf
1 2
1 2
1 2
E1
(1)
A*
A
Abb. 1.22: Induzierte Emission eines Photons
Mit anderen Worten: Bei der induzierten Photonenemission entsteht
kohärente Strahlung, d. h. beide Photonen stimmen in Energie, Ausbreitungsrichtung und Phasenlage überein. Ihre elektrischen und
magnetischen Felder schwingen dann im Takt. Treffen diese auf
andere angeregte Atome im Zustand (2), so können auch diese zur
induzierten Photonenemission stimuliert werden. Sind ausreichend
viele angeregte Atome vorhanden, kann durch diesen Prozess die
Anzahl der sekundären Photonen lawinenartig anwachsen. Allerdings wirkt dieser Lichtverstärkung der gegenläufige Prozess der
Photonenabsorption entgegen, denn die Rate der induzierten Emissionsprozesse ist der Anzahl der angeregten Atome, die Rate der Absorptionsvorgänge der Anzahl der Atome im Grundzustand proportional. Im Normalfall übertrifft die Anzahl der Atome im Grundzustand bei weitem die Anzahl der angeregten Atome, so dass die Absorption der einfallenden Strahlung über die stimulierte Emission
dominiert. Lichtverstärkung der einfallenden Strahlung ist daher nur
bei Besetzungsinversion möglich, d. h. es befinden sich mehr Atome
im angeregten Zustand als im Grundzustand. Die Überführung der
Atome oder Moleküle eines Stoffes in einen Zustand mit Besetzungsinversion ist durch geeignete technische Maßnahmen wie beispielsweise optisches Pumpen möglich. Dabei wird dem Stoff von
außen Anregungsenergie in Form einer intensiven elektromagnetischen Strahlung zugeführt. Eine Strahlungsquelle mit einem aktiven
Medium aus Atomen / Molekülen mit Besetzungsinversion wird
Laser genannt. Es handelt sich dabei um ein Akronym der englischen
Bezeichnung Light amplification by stimulated emission of radiation
(Lichtverstärkung durch erzwungene Emission von Strahlung).
Je nach Art des aktiven Mediums, in dem die Lichtverstärkung erzeugt wird, unterscheidet ,man Festkörper-, Dioden-, Gas- und
Farbstofflaser. Das aktive Medium befindet sich in einem optischen
Resonator, der im einfachsten Fall aus einem Paar paralleler Spiegel
besteht, die auf einer optischen Achse angeordnet sind. Durch Reflexion an den Spiegeln durchläuft die primäre Lichtwelle das aktive
Medium mit Besetzungsinversion immer wieder. Sie wird dabei
durch induzierte Emission kontinuierlich verstärkt, bevor sie durch
einen der beiden Spiegel, der halbdurchlässig ausgelegt ist, ausge-
40
1.4 Laser
koppelt wird. Der dabei entstehende Laserstrahl stellt einen Photonenstrom von hoher Intensität (Energieflussdichte), scharfer Bündelung und extrem schmalbandigem Frequenzbereich dar, ist also quasi
monochromatisch. Je nach Betriebsart sind kontinuierliche Dauerstrich-Laser und gepulste Laser mit Pulsdauern bis zu 1 ⋅ 10 −12 s zu
unterscheiden.
Die grundlegende Idee zur technischen Realisierung eines Lasers
wurde 1958 von Arthur Schawlow und Charles Townes veröffentlicht. Der erste Laser wurde 1960 von Theodore Maiman entwickelt.
Es handelte sich dabei um den Rubin-Laser, einen Festkörperlaser,
dessen aktives Medium ein Saphirkristall ist, der aus Aluminiumoxid
(Al2O3) besteht und bei dem etwa 0,04 % der Al+++-Ionen durch
Cr+++-Ionen substituiert werden. Ein stabförmiger Rubinkristall ist
von einer Blitzlampe in Form einer spiralförmigen Gasentladungsröhre umgeben, welche die optische Pumpleistung zur Erzeugung der
Besetzungsinversion liefert. Abb. 1.23 zeigt das vereinfachte Termschema der Chrom-Atome im Rubinkristall.
Energie
Energie
e
Elektronenanregung
(3)
(3)
e
strahlungsloser
Übergang
(2)
induzierter
Übergang
hf
1 2
(1)
Grundzustand
(1)
Abb. 1.23: Termschema der Cr-Atome im Rubin-Laser
Unter einem Termschema eines Atoms versteht man die Darstellung
der möglichen Energiewerte auf einer vertikalen Energieskala durch
horizontale Striche. Die elektronischen Übergänge zwischen den
Energiezuständen sind als vertikale Pfeile eingetragen. Durch das
intensive Pumplicht der Blitzlampe werden die Elektronen durch
Photonenabsorption aus dem Grundzustand (1) in das breite Band (3)
der angeregten Zustände gehoben. Dadurch wird der Grundzustand
entvölkert. Unter Energieabgabe an den Kristall in Form von Wärme
gehen die Elektronen dann bevorzugt strahlungslos in den metastabi-
len Zustand (2) über, dessen Lebensdauer etwa 10 5 mal größer ist
als in Zustand (3). Dort sammeln sie sich an, sodass sich im Zustand
(2) nach kurzer Zeit mehr Elektronen befinden als im Grundzustand
(1). Damit ist die für die Lasertätigkeit notwendige Besetzungsinversion realisiert. Spontane Photonenemission von (2) nach (1) verursacht dann die stimulierte Emission. Die beim induzierten Übergang
41
1 Atomphysik
von (2) nach (1) mit der Energie ∆E = h ⋅ f12 emittierten Photonen
der Laserstrahlung besitzen eine Wellenlänge von λ = 694 nm . In
Tabelle 1.3 sind einige technisch wichtigen Lasertypen aufgeführt.
Typ
Aktives Medium
Wellenlänge
Festkörper-Laser
YAG-Neodym
1,064 µm
Dioden-Laser
Gallium-Arsenid
780 nm
Gas-Laser
Helium-Neon
633 nm
Stickstoff ( N 2 )
337 nm
Kohlendioxid ( CO 2 )
10,6 µm
Tab.: 1.3: Verschiedene Lasertypen
Von den vielfältigen Laser-Anwendungen seien folgende Beispiele
genannt: Barcode-Scanner, Audio-CD-Player, CD-ROM- und DVDLaufwerke, Geräte für die Vermessungstechnik, die Umweltüberwachung und die optische Datenübertragung durch Glasfaser-Kabel
sowie Vorrichtungen zum Schneiden, Schweißen und Härten von
Metallen.
1.5
Röntgenstrahlung
Wilhelm Conrad Röntgen entdeckte 1895 in Würzburg eine durchdringende elektromagnetische Strahlung im Wellenlängenbereich
von 10–9 m bis 10–11 m, die nach ihm benannte Röntgenstrahlung.
Diese Strahlung kann in einer Röntgenröhre erzeugt werden. Sie
besteht aus einem evakuierten Glaskolben, in dem aus einer Kathode
durch Glühemission Elektronen austreten, die durch eine hohe elektrische Spannung UA zur Anode hin beschleunigt werden.
Cu
Kathode
–
W
Anode
+
HO
2
Glaskolben
evakuiert
Röntgenstrahlung
Abb. 1.24: Aufbau einer Röntgenröhre
Beim Auftreffen auf die Anode besitzen sie die Energie Ekin = e UA,
die bei den zur Abbremsung der Elektronen führenden Stoßprozessen
mit den Atomen der Anode teilweise in Röntgenstrahlung umgewan-
42
1.5 Röntgenstrahlung
delt wird. Die Röntgenstrahlung entsteht in der Atomhülle. Sie entsteht aus der Überlagerung eines kontinuierlichen Spektrums, der
Röntgenbremsstrahlung, die im kurzwelligen Bereich durch eine
minimale Wellenlänge λ min begrenzt wird, und eines Linienspektrums, das durch das Anodenmaterial bestimmt wird und deshalb
charakteristische Röntgenstrahlung (Abb. 1.25) genannt wird.
I
K
K
Kγ
min
Abb. 1.25: Schematisches Spektrum einer Röntgenröhre
1.5.1
Röntgenbremsstrahlung
Die Röntgenbremsstrahlung entsteht bei der Abbremsung von
schnell bewegten Elektronen im elektrischen Feld der Atomkerne.
Die maximale Röntgenstrahlungsenergie E = h ⋅ f max entsteht dann,
wenn das Elektron seine gesamte beim Durchlaufen der zwischen
Kathode und Anode anliegenden elektrischen Spannung U A aufgenommene kinetische Energie e ⋅ U A in einem Stoßprozess abgibt und
diese vollständig in elektromagnetische Strahlungsenergie umgewandelt wird. Es gilt dann:
h ⋅ f max = e ⋅ U A
f max =
λ min =
c
f max
c
λ min
=
h⋅c
.
e ⋅U A
(1.41)
(1.42)
(1.43)
Das kontinuierliche Röntgenbremsspektrum besitzt eine kurzwellige
Grenze λmin, die so genannte Grenzwellenlänge. Sie hängt nur von
der beschleunigenden Anodenspannung, nicht jedoch vom Anodenmaterial der Röntgenröhre ab.
43
1 Atomphysik
1.5.2
Charakteristische Röntgenstrahlung
Das auf die Anode auftreffende Elektron kann beim Stoßprozess ein
Elektron aus einer voll besetzten – inneren – Schale schlagen, wenn
die beim Stoß übertragene Energie die Bindungsenergie des Hüllenelektrons überschreitet. Die dabei durch Ionisierung entstehende
Lücke in der K- oder L-Schale wird sofort von Elektronen der weiter
außen liegenden Schalen aufgefüllt, und zwar unter Emission von
elektromagnetischer Strahlung mit für das Anodenmaterial charakteristischen Frequenzen bzw. Wellenlängen. Durch den Übergang
eines äußeren Hüllenelektrons in die Lücke wird Energie freigesetzt,
da die äußeren Elektronen schwächer gebunden sind als die inneren.
Die Bindungsenergie der Hüllenelektronen nimmt mit dem Abstand
vom Atomkern nach außen hin ab; das charakteristische Spektrum ist
daher vom Anodenmaterial abhängig. Seine Linien überlagern sich
dem kontinuierlichen Bremsspektrum. Die (K-, L-, M-, ...)Schale, in
der sich die Leerstelle befindet, gibt der betreffenden Röntgenlinie
den Namen. Die Herkunft des auffüllenden Elektrons wird durch
einen griechischen Index ( α, β, γ ,... ) gekennzeichnet.
In Erweiterung der Balmerformel erhält man für wasserstoffähnliche
Ionen mit der Kernladung Z, in deren Hülle sich nur ein einziges
Elektron befindet:
∆E = hf = E m − E n = − R H Z 2 (
1
m
2
−
1
n2
)
(1.44)
∆E ist die Photonenenergie, die beim Übergang des Elektrons aus
der m-ten Bahn mit der Gesamtenergie Em in die n-te Bahn
(m > n) mit der Gesamtenergie En emittiert wird.
Für die diskreten Röntgenenergien E K der K-Serie gilt:
EK α = h ⋅ f = EL − E K
(1.45)
EKβ = h ⋅ f = E M − E K
EK γ = h ⋅ f = E N − E K
M
M
M
M
Wie die Bindungsenergien der Elektronen hängen auch die Energien
der Röntgenquanten von der Ordnungszahl Z der Atome des Anodenmaterials ab. Für die Energien der K-Serie (n = 1, m = 2, 3, 4,
... entsprechend den Bezeichnungen α, β, γ ,... ) gilt das Moseley-
sche Gesetz:
E K ,m = hf = E m − E1 = − R H ( Z − 1) 2 (
1
m2
− 1)
(1.46)
Der mit der Emission der Röntgenstrahlung verbundene Übergang
eines Hüllenelektrons in die K-Schale des Atoms setzt einen unbe-
44
1.6 Übungsaufgaben zu Kapitel 1
setzten Platz (Zustand) in der K-Schale voraus. Durch Stoßionisation
mit hochenergetischen Elektronen oder Photonen wie γ -Quanten
können Elektronen der inneren Schalen aus dem Atomverband freigesetzt werden. Das in der Nähe des Atomkerns verbleibende KSchalenelektron schirmt dann die wirksame Kernladung Z um eine
Einheit ab. Diese Abschirmung führt dazu, dass ein äußeres Hüllenelektron nur der anziehenden Wirkung einer reduzierten Kernladung (Z – 1) unterliegt. Mit wachsender Schalennummer (Hauptquantenzahl) m nimmt die Energie des Hüllenelektrons zu und seine
Bindungsenergie ab. Für m → ∞ erreicht man den ungebundenen
Zustand, der auch als Grenzkontinuum bezeichnet wird. Im zugehörigen Röntgenspektrum erscheint die so genannte K-Kante mit der
maximalen Grenzenergie EK = RH ( Z − 1)2 . Für die Energien der
langwelligsten K-Linie (m = 2), der K α - Strahlung, liefert das Moseleysche Gesetz:
E K = hf =
α
3
R H ( Z − 1) 2 = 10,2 ⋅ ( Z − 1) 2 eV
4
(1.47)
Das Moseleysche Gesetz erlaubt aus der Messung der Energie der
K α -Röntgenstrahlung die Bestimmung der Ordnungszahl Z und
ermöglicht damit eine atomphysikalische Elementbestimmung.
1.6
Übungsaufgaben zu Kapitel 1
Aufgabe 1
Das digitale Mobilfunknetz E-Plus benutzt Funkfrequenzen von
1800 MHz. Welche Wellenlänge hätten diese Funksignale, wenn
es sich um analoge elektromagnetische Wellen handeln würde?
Aufgabe 2
Aus einer Cäsium-Photokathode mit einer Austrittsarbeit von
W A = 1,94 eV sollen Photoelektronen freigesetzt werden.
a) Bestimmen Sie die größte Wellenlänge, mit der dies gerade
noch möglich ist.
b) Welche kinetische Energie in eV besitzen die Photoelektronen
bei Bestrahlung mit UV-Licht der Wellenlänge λ = 300 nm?
Aufgabe 3
Welchen Radius besitzt die 3. Bohrsche Bahn im H-Atom?
45
1 Atomphysik
Aufgabe 4
Berechnen Sie den Radius der 1. Bohrschen Bahn eines Elektrons im
zweifach geladenen Lithium-Ion (Li++), dem zwei Elektronen infolge
von Ionisationsprozessen entrissen wurden.
Aufgabe 5
a) Wie viele erlaubte Möglichkeiten der Emission von Lichtquanten
besitzt ein H-Atom im angeregten Zustand, wenn sich sein Elektron in der 3. Bohrschen Bahn befindet?
b) Wie viele Lichtquanten mit unterschiedlicher Strahlungsenergie
treten dabei auf?
Aufgabe 6
a) Beschriften Sie in dem schematischen Energieterm-Schema
(Abb. 1.22) die besetzten Hauptschalen mit den entsprechenden
lateinischen Buchstaben!
b) Geben Sie die detaillierte Elektronenkonfiguration von Natrium
an!
H
He
Li
Ne
Na
a)
b)
c)
d)
e)
Abb. 1.26: Energietermschema
Aufgabe 7
Können He-Atome nach entsprechender Anregung charakteristische
Röntgenstrahlung emittieren? Begründen Sie Ihre Antwort!
Aufgabe 8
Bestimmen Sie die Wellenlänge der Strahlung, die beim Übergang
eines ionisierten Wasserstoffatoms (H+) in den Grundzustand durch
Einfang eines freien (ruhenden) Elektrons emittiert wird!
46
1.7 Musterlösungen zu Kapitel 1
Aufgabe 9
Ein He-Ne-Laser strahlt Photonen mit einer Frequenz von
f = 474 THz ab.
a) Welche Wellenlänge besitzt diese Strahlung?
b) Welche Energie transportieren die Photonen in den Einheiten
Ws und eV?
c) Aus wie vielen Photonen besteht ein Rechteckimpuls von 0.1 ms
Dauer bei einer abgegebenen Strahlungsleistung des Lasers von
100 kW?
Aufgabe 10
Der Elektronenstrahl einer Farbfernseh-Bildröhre wird mit einer
Anodenspannung von U A = 26 kV beschleunigt und trifft dann auf
die Innenseite des Bildschirmes. Geben Sie die kürzest mögliche
Wellenlänge der dabei entstehenden Röntgenstrahlung an!
Aufgabe 11
Ein kreisförmiger CO2-Laserstrahl mit einem Durchmesser von
2 mm trifft mit einem Rechteckimpuls von 1 ns Dauer und der Energie von 100 kJ auf eine zu bearbeitende Metallprobe.
a) Wie viele Photonen treffen pro Laserpuls auf die Probe?
b) Wie groß ist die Intensität (flächenbezogene Energiestromdichte) des Laserstrahls?
1.7
Musterlösungen zu Kapitel 1
Aufgabe 1
λ⋅ f =c
f = 1800 MHz = 1,8 ⋅10 9 Hz
λ=
c 3 ⋅ 10 8 m / s
=
= 1,66 ⋅ 10 −1 m
f 1,8 ⋅ 10 9 1/ s
Aufgabe 2
a) Die Photonen müssen eine Mindestenergie E = h ⋅ f besitzen,
die der Austrittsarbeit WA der Photoelektronen entspricht.
E = h ⋅ f = WA
f =
c
λ
47
1 Atomphysik
WA =
hc
λ
W A = 1,94 eV = 1,94 eV ⋅1,602 ⋅10 −19 J / eV = 3,1 ⋅10 −19 J
Alle Photonen mit einer Wellenlänge λ < λ max können Elektronen
freisetzen.
λ max =
b)
hc 6,626 ⋅10 −34 Js ⋅ 3 ⋅10 8 m / s
=
= 6,41 ⋅10 −7 m = 641 nm
−19
WA
3,1 ⋅10
J
E kin = E − W A = h ⋅ f − W A
Für die Photonenenergie E gilt:
E = hf =
hc
λ
6,626 ⋅ 10 −34 Js ⋅ 3 ⋅ 10 8
=
3,00 ⋅ 10 −7 m
m
s = 6,626 ⋅ 10 −19 J = 4,14 eV
Für die kinetische Energie der Photoelektronen folgt:
E kin = E − W A = 4,14 eV − 1,94 eV = 2,20 eV
Aufgabe 3
Für die n-te Bohrsche Bahn im H-Atom gilt:
r (n) = rn =
4πε 0h 2
me e2
n2
Mit den Konstanten:
h = 1,055 ⋅10 −34 Js
m = 9,1 ⋅10 −31 kg
ε 0 = 8,854 ⋅ 10 −12
As
Vm
folgt:
rn = 0,53 ⋅10 −10 m ⋅ n 2
Für n = 3 erhält man r3 = 4,77 ⋅10 −10 m .
Aufgabe 4
Für die Bohrschen Radien r(n) im Coulombschen Feld eines Kerns
der Kernladungszahl Z gilt:
48
1.7 Musterlösungen zu Kapitel 1
r (n) = rn =
4πε 0h 2
me Ze 2
n 2 = 0,53 ⋅ 10−10 m ⋅
n2
Z
Für n = 1 und Z = 3 (Lithium) folgt:
r1 = 0,18 ⋅10 −10 m .
Aufgabe 5
a) 4
b) 3
Aufgabe 6
a) In dem schematischen Energieterm-Modell sind folgende Hauptschalen besetzt: a) K-Schale, b) K-Schale, c) K- und L-Schale,
d) K- und L-Schale, e) K-, L- und M-Schale
b) Die Elektronenkonfiguration von Natrium lautet:
1s 2 2 s 2 2 p 6 3s 1
Aufgabe 7
Die energiereichste charakteristische Röntgenstrahlung gehört zur KSerie. Für die Energien der K-Serie gilt das Moseleysche Gesetz:
E K ,m = h ⋅ f = E m − E1 = − R H ( Z − 1) 2 (
1
m2
− 1)
Für m → ∞ erscheint im charakteristischen Röntgenspektrum die
K-Kante mit der maximalen Grenzenergie
E K = R H ( Z − 1) 2 = 13,6 eV ⋅ ( Z − 1) 2 .
Für Helium ist Z = 2, und damit ist E K = 13,6 eV . Es handelt sich
hierbei um eine harte UV-, nicht aber um Röntgenstrahlung.
Aufgabe 8
Beim Einfang eines freien (ruhenden) Elektrons durch ein ionisiertes
H-Atom (H+) wird gerade die Bindungsenergie des Elektrons im HAtom von 13,6 eV frei. Geht das Elektron direkt in den Grundzustand des H-Atoms über, so folgt für die Energie E des emittierten
Photons:
49
1 Atomphysik
E = 13,6 eV = 2,18 ⋅10 −18 J .
Wegen E = h ⋅ f und λ ⋅ f = c folgt:
λ=
h ⋅ c 6,626 ⋅10 −34 Js ⋅ 3 ⋅10 8 m / s
=
= 9,12 ⋅10 −8 m = 91,2 nm
−
18
E
2,18 ⋅10
J
Aufgabe 9
a)
λ⋅ f =c
λ=
b)
3 ⋅10 8 m / s
c
=
= 0,633 ⋅10 −6 m = 633 nm
f 4,74 ⋅1014 1 / s
E =h⋅ f
= 6,626 ⋅ 10 −34 Js ⋅ 4,74 ⋅ 1014 1 / s = 3,14 ⋅ 10 −19 J = 1,96 eV
c) Die Strahlungsleistung des Lasers ist gegeben durch
P = ∆E / ∆t .
Dann ist die während der Pulsdauer ∆t = 0,1 ms abgegebene
Photonenenergie ∆E = P ⋅ ∆t = 100 kW ⋅ 0,1 ms = 10 Ws = 10 J .
Nach Aufgabenteil (b) transportiert jedes Photon die Energie
E = 3,14 ⋅10 −19 J .
Der Rechteckpuls besteht daher aus
N=
10 J
∆E
=
= 3,18 ⋅1019 Photonen.
−19
E
3,14 ⋅10
J
Aufgabe 10
Die Grenzwellenlänge des kontinuierlichen Röntgenbremsspektrums
ergibt sich gemäß
λmin =
λmin =
c
h ⋅c
=
fmax U A ⋅ e
6,626 ⋅ 10 −34 Js ⋅ 3 ⋅ 10 8 m / s
3
26 ⋅ 10 V ⋅ 1,6 ⋅ 10
−19
As
=
19,878 ⋅ 10 −26 Jm
41,6 ⋅ 10 −16 Ws
= 0,478 ⋅ 10 −10 m
Aufgabe 11
Die Photonen des CO2-Lasers besitzen eine Wellenlänge von
λ = 10,6 µm . Sie transportieren jeweils eine Energie
50
1.7 Musterlösungen zu Kapitel 1
E = hf =
hc
λ
= 1,875 ⋅10 − 20 J .
a) Der Rechteckimpuls besitzt eine Energie ∆E = 100 kJ . Folglich
100 ⋅10 3 J
∆E
=
= 5,33 ⋅10 24
E 1,875 ⋅10 − 20 J
Photonen auf die Metallprobe.
treffen pro Laserpuls N =
b) Der Laserpuls besitzt eine Leistung von
P=
∆E 100 kJ
=
= 100 TW .
∆t 10 −9 s
Die Intensität I entspricht der flächenbezogenen Energiestromdichte
(Leistung pro Fläche). Die Fläche A des Laserstrahls beträgt A =
3,14 mm2. Damit ergibt sich für die Intensität
I=
100 ⋅1012 W
P 100 ⋅1012 W
=
=
= 3,18 ⋅1019 W / m 2 .
2
−6
2
A
3,14 mm
3,14 ⋅10 m
51
2 Kernphysik
2
Kernphysik
2.1
Aufbau der Atomkerne
Ein Atomkern ist vollständig charakterisiert, wenn man die Zahl
seiner Protonen und Neutronen kennt. Die Nukleonenzahl
A = Z + N gibt an, wie viele Nukleonen ein Kern enthält. Sie wird
auch als Massenzahl bezeichnet. Die Neutronenzahl N ergibt sich
aus der Differenz von Nukleonenzahl A und Protonenzahl Z zu
N = A – Z.
Die Vorstellung, dass Atomkerne aus Protonen und Neutronen aufgebaut sind, wurde 1932 von Werner Heisenberg entwickelt, nachdem im selben Jahr James Chadwick in künstlich ausgelösten Kernreaktionen ein neues, elektrisch neutrales Elementarteilchen, nämlich
das Neutron entdeckte.
Als Isotope bezeichnet man die Nuklide, die sich in der Zahl der
Neutronen N, nicht aber in der Zahl der Protonen Z voneinander unterscheiden. Isotope gehören daher stets zum gleichen chemischen
Element. Die Nukleonen werden durch die Kernkräfte im Atomkern
gebunden.
2.2
Kernkraft und Bindungsenergie
Atomkerne sind aus elektrisch positiv geladenen Protonen und
elektrisch neutralen Neutronen aufgebaut. Sie bilden die zusammenfassend als Nukleonen bezeichneten Kernbausteine. Da zwischen den
Protonen aufgrund ihrer gleichnamigen elektrischen Ladung abstoßende Coulombkräfte wirken, ist der Zusammenhalt stabiler Atomkerne nur durch die Wirkung anziehender Kräfte möglich, die stärker
sind als die elektrische Coulomb-Abstoßung. Zur Erklärung dieses
Phänomens musste eine neue Kraft eingeführt werden, die so genannte Kernkraft. Durch eine Vielzahl von experimentellen Untersuchungen konnten die Eigenschaften dieser Kernkraft ermittelt werden. Es handelt sich dabei um eine starke anziehende Kraft, die in
gleicher Weise zwischen Proton und Proton (p-p), Proton und Neutron (p-n) sowie Neutron und Neutron (n-n) wirkt. Sie ist somit unabhängig von der elektrischen Ladung der Nukleonen. Inzwischen
konnte experimentell nachgewiesen werden, dass die Nukleonen eine
innere Struktur besitzen und sich aus subnuklearen Elementarteilchen, den sog. Quarks zusammensetzen. Als kleinste Bausteine der
Materie gelten heute somit die Quarks und die Leptonen (leptos:
grch. leicht). Zu den Leptonen zählen die Elementarteilchen, die
keine starke Wechselwirkung besitzen und somit die Kernkraft nicht
spüren, wie das Elektron und das Neutrino. Die Existenz von jeweils
sechs verschiedenen Quarks und sechs Leptonen konnte inzwischen
52
2.2 Kernkraft und Bindungsenergie
experimentell gesichert nachgewiesen werden. Die meisten von
ihnen dienen zur Erklärung von extrem kurzlebigen Teilchen, die in
Hochenergiebeschleunigern erzeugt oder in der kosmischen Strahlung beobachtet wurden.
Für den Aufbau der uns umgebenen “stabilen“ Materie werden nur
drei Elementarteilchen benötigt. Neben dem Elektron sind dies das
„Up“-Quark mit einer elektrischen Ladung q u = +2 / 3 e und das
„Down“-Quark mit einer elektrischen Ladung q d = −1 / 3 e . Die
drittelzahligen Ladungen sind das charakteristische Merkmal der
Quarks. Freie Quarks scheinen in der Natur jedoch nicht vorzukommen. Sie treten nur als Konstituenten von den der starken Wechselwirkung unterliegenden Teilchen, den Hadronen (hadros: grch.
schwer, stark) auf. So sind sowohl das Proton (p = udu) als auch das
Neutron (n = dud) jeweils aus drei Quarks aufgebaut.
Proton
Neutron
u
d
u
d
d
u
Abb. 2.1: Aufbau von Proton und Neutron aus drei Quarks
Zwischen diesen Quarks wirkt eine fundamentale Kraft, die als starke Wechselwirkung bezeichnet wird. Die zwischen den Nukleonen
eines Atomkerns wirkende Kernkraft wird als Restwechselwirkung
der zwischen ihren Quarkkonstituenten wirksamen starken Wechselwirkung interpretiert. Die Kernkraft kann daher nicht durch ein
einfaches Kraftgesetz beschrieben werden. Sie ist weder elektrischer
noch magnetischer Natur und kann auch nicht durch die Gravitation
erklärt werden. Die Kernkraft stellt somit eine neue Qualität der Materie dar. Träger dieser Eigenschaft sind die Nukleonen. Die wichtigste Eigenschaft der Kernkraft ist ihre kurze Reichweite. Die Wirkung der Kernkraft ist auf den Atomkern beschränkt. Für Abstände
r > RK, d. h. außerhalb der Atomkerne ist die Kernkraft praktisch
nicht mehr nachweisbar, während die elektrostatischen Coulombkräfte, die mit 1/r2 abfallen, eine unendlich ausgedehnte Reichweite
besitzen. Die Folge hiervon ist, dass sich Protonen in großer Entfernung elektrostatisch abstoßen, in kurzer Distanz jedoch anziehen, da
die Bindungskraft der Kernkraft erheblich größer ist als die
Coulomb-Abstoßung.
53
2 Kernphysik
Die Dichte ρ K =
mK
VK
aller Atomkerne ist näherungsweise konstant.
Hierbei ist m K ist die Masse, V K =
4π 3
R das Volumen und R K
3 K
der Radius des Atomkerns.
Die Größe ρ K wird auch als die Dichte der Kernmaterie bezeich4π 3
r das Volumen eines Nukleons, so folgt für das
3 0
Volumen VK eines Atomkerns mit A Nukleonen
net. Ist V0 =
V K = V0 A
oder
4π 3 4π 3
R =
r A
3 K
3 0
VK =
(2.1)
Damit erhält man für den Kernradius RK die Beziehung
R K = r0 A1 / 3 .
(2.2)
Für die Radiuskonstante r0 erhält man aus Streuexperimenten den
Wert
r0 = 1,5 ⋅ 10 −15 m = 1,5 fm .
(2.3)
Während der Atomradius eine Größe von etwa R A ≈ 10 −10 m aufweist, liegt die Größe des Atomkerns nur bei etwa R K ≈ 10 −15 m.
Damit ist das Atomvolumen etwa 1015-mal größer als das Kernvolumen.
Wenn die Nukleonenmasse m n = m p = mu gleich der Atommassenkonstante m u gesetzt wird, ergibt sich die Kernmasse m K eines
Atomkerns mit A Nukleonen zu m K = A ⋅ mu .
Mit mU = 1,66 ⋅10 −27 kg erhält man dann für die Dichte der Kernmaterie:
ρK =
mK
VK
=
A ⋅ mu
4π 3
r ⋅A
3 0
≈ 1 ⋅1017
kg
m3
.
(2.4)
Diese riesige Dichte ist sicherlich nur möglich, wenn die Nukleonen
im Atomkern durch extrem starke Kräfte zusammengehalten werden,
nämlich die Kernkräfte.
54
2.2 Kernkraft und Bindungsenergie
Die Packungsdichte der Nukleonen in den Atomkernen ist unabhängig von der Größe der Atomkerne. Auch die mittlere Bindungsenergie pro Nukleon ist für alle Kerne (mit Ausnahme der ganz leichten)
nahezu gleich. Diese experimentellen Befunde können nur so interpretiert werden, dass die Kernkraft nur eine geringe Reichweite hat.
Jedes Nukleon im Atomkern erfährt nur eine Kraftwirkung von den
unmittelbaren Nachbarn. Die von dem betrachteten Nukleon weiter
entfernt befindlichen Nukleonen haben keinen Einfluss. Diese Eigenschaft der Kernkraft konnte auch durch Nukleon–Nukleon–Streuexperimente erhärtet werden. Wegen ihrer Kleinheit bleiben die
Atomkerne der direkten Anschauung verborgen. Daran ändern auch
instrumentelle Hilfsmittel nichts. Informationen aus dem subatomaren Bereich können nur in großen Beschleunigeranlagen gewonnen
werden, in denen Elementarteilchen auf große Energien beschleunigt
werden, um dann als Sonden in die Atome geschossen zu werden.
Aus den Reaktionen dieser Sonden mit den Atomkernen lassen sich
Rückschlüsse auf den Aufbau der Atomkerne und die Struktur der
Kernkraft ableiten.
Bereits 1909 experimentierten Ernest Rutherford, Ernest Marsden
und Hans Geiger mit der kurz zuvor entdeckten α-Strahlung radioaktiver Substanzen. Die α-Strahlung besteht aus schnell bewegten
Atomkernen des Elements Helium, die beim α-Zerfall schwerer
radioaktiver Atome ausgesandt werden können. Beim Beschuss von
dünnen Goldfolien, so genannter Targets (engl. Zielscheiben), wurden gelegentlich große Ablenkwinkel der α-Teilchen beobachtet.
1911 beschrieb Rutherford im Philosophical Magazine diese
Streuexperimente und gab eine Deutung der beobachteten Streuung
der
α-Teilchen, die die empirische Grundlage des Rutherfordschen
Atommodells legte.
α-Teilchen
radioaktive Quelle
Goldfolie
Blei-Kolimator
Zinksulfid-Schirm
Abb. 2.2: Rutherfordsches Streuexperiment
Entgegen den Erwartungen von Dalton, nach denen die Atome als
harte, undurchdringliche Kugeln aufgefasst wurden, durchdringen
55
2 Kernphysik
die meisten α-Teilchen ohne jegliche Ablenkung die Goldfolie. Dieser Sachverhalt ist schematisch in Abb. 2.3 stark vergrößert dargestellt.
Abb. 2.3: Interpretation der Streuexperimente von Rutherford
Die Atome besitzen offensichtlich eine innere Struktur. In ihrem
Zentrum ist ein elektrisch positiv geladener Atomkern lokalisiert,
dessen Größe aus der Analyse der Streudaten extrahiert werden kann.
Dieser ist von einer ausgedehnten Atomhülle, der Elektronenhülle,
umgeben, die überwiegend aus leerem Raum besteht.
Die gestreuten α-Teilchen treffen bei diesem Experiment auf einen
Zinksulfid-Schirm und rufen dort Szintillationen (lat. szintillare =
flimmern, blitzen) genannte Lichtblitze hervor. Detektoren, die zum
Nachweis von auftreffenden ionisierenden Teilchen optisch wahrnehmbare Lichtblitze registrieren werden Szintillationszähler oder
kurz Szintillatoren genannt.
Derartige Streuexperimente sind für die Atom-, Kern- und Elementarteilchenphysik von fundamentaler Bedeutung. Aus der Trefferwahrscheinlichkeit und der Winkelverteilung der gestreuten Teilchen
gewinnt man Informationen über Größe und Struktur der beschossenen Streuzentren des Targetmaterials. Werden beispielsweise die
Atome eines Wasserstoffgases als Zielscheibe dem Beschuss von in
elektrischen Feldern von Beschleunigeranlagen auf große Bewegungsenergie gebrachten Protonen ausgesetzt, so kann aus solchen
Proton-Proton-Streuexperimenten die Reichweite der Kernkraft zwischen den Nukleonen indirekt gemessen werden. Sie beträgt etwa
1,5 ⋅ 10 −15 m. Für größere Abstände fällt die Kernkraft auf Null ab.
Für kleinere Abstände ist sie zunächst stark anziehend, um dann bei
sehr kleinen Abständen unterhalb des Nukleonenradius stark abstoßend zu werden. Diese Abstoßung bei kleinsten Abständen wird als
Hard-Core-Repulsion bezeichnet. Wäre die Kernkraft auch für
kleinste Abstände nur anziehend, würden die Atomkerne keine
56
2.2 Kernkraft und Bindungsenergie
messbare Ausdehnung aufweisen und auf den Radius Null mit unendlicher Dichte der Kernmaterie schrumpfen.
Die Kernphysik stellt sich demnach als eine Art Nukleonenchemie
dar. Aus einem Baukasten von freien Neutronen und Protonen können die Atomkerne zusammengesetzt oder synthetisiert werden. Dabei wird als Folge der stark anziehenden Kernkraft die Bindungsenergie EB frei. Bei der Kernsynthese aus einem Nukleonengas wird
die Bindungsenergie in Form elektromagnetischer Strahlung abgegeben. Wegen der Größe der Kernkraft ist auch die Bindungsenergie
sehr groß. Aufgrund einer von A. Einstein 1905 gefundenen Beziehung, die die Äquivalenz von Energie E und Masse m beschreibt,
gilt:
E = mc 2 .
(2.5)
Energie und Masse sind einander proportional. Die Proportionalitätskonstante ist das Quadrat der Lichtgeschwindigkeit c. Diese für
die gesamte Kernphysik fundamentale Beziehung folgt theoretisch
aus der von Einstein formulierten speziellen Relativitätstheorie. Dort
konnte gezeigt werden, dass die Masse m eines Objektes von seiner
Geschwindigkeit v abhängig ist. Quantitativ gilt für diese Geschwindigkeitsabhängigkeit die Beziehung
m=
m0
1−
v2
.
(2.6)
c2
m0 ist dabei die Ruhemasse. Diese Beziehung ist für subatomare
Teilchen von besonderer Bedeutung. In Abbildung 2.4 ist die experimentell ermittelte Abhängigkeit der Elektronenmasse me von der
Geschwindigkeit gezeigt.
m/m
e
3,0
2,0
1,0
0
0
0,25
0,5
0,75
1,0
v/c
Abb. 2.4: Abhängigkeit der Elektronenmasse m von der Geschwindigkeit v
57
2 Kernphysik
Für makroskopische Körper ist wegen v << c stets m = m0. In der
klassischen Mechanik wird ausschließlich mit diesem nichtrelativistischen Grenzfall gerechnet. Bei Beschränkung auf lineare Bewegungen erhält man mit Hilfe des 2. Newtonschen Axioms unter Berücksichtigung der Geschwindigkeitsabhängigkeit der Masse
F=
d
d m0 ⋅ v
m⋅v =
dt
dt
v2
1− 2
c
{
F = m0 (1 −
F=
m0 ⋅
v2
1
v 2 −3 / 2 2v dv
−1 / 2
)
+
m
v
[
−
(
1
−
)
(− 2 )]}
0
2
dt
c2
c2
c
dv
dt
 v2 
1 −

 c2 


32
Bewegt sich ein Körper im Zeitintervall zwischen t1 und t2 vom Ort
s1 nach s2 und verändert dabei infolge der Krafteinwirkung F seine
Geschwindigkeit von v1 aus v2, so ändert sich die Gesamtenergie des
Körpers um ∆E , und es gilt:
s
t
s1
t1
m0
∆E = ∫ 2 F ⋅ ds = ∫ 2
∆E =
m0 c 2
1−
v 22
c2
−
(1 −
m0 c 2
1−
v12
dv
dt
v2
c2
)
m0 v
v ⋅ dt = ∫
3/ 2
(1 −
v2
c2
)
dv
3/ 2
= (m 2 − m1 ) ⋅ c 2 = ∆m ⋅ c 2
c2
Ist speziell v1 = 0 und v2 = v, so folgt für die relativistische kinetische
Energie ∆E eines Teilchens mit der Ruhemasse m0
∆E = mc 2 − m0 c 2 .
Durch eine geeignete Wahl des Energie-Nullpunktes kann dem ruhenden Körper eine Ruheenergie E 0 = m0 ⋅ c 2 zugewiesen werden.
Die relativistische Gesamtenergie E = E0 + ∆E ergibt sich dann zu
E = (m 0 + ∆m)c 2 = mc 2 .
Vergleicht man die Masse eines bestimmten Atomkerns
(2.7)
A
X
Z
, in dem
A = N + Z Nukleonen im gebundenen Zustand vorliegen, mit der
58
2.2 Kernkraft und Bindungsenergie
Masse von Z freien Protonen und N freien Neutronen, dann stellt
man eine Massendifferenz ∆m fest:
( Zm p + Nm n ) − m( ZA X ) = ∆m
(2.8)
Die Größe ∆m gibt an, um wie viel sich die Masse eines Kerns von
der Summe der Massen seiner Nukleonen unterscheidet. ∆m wird
Massendefekt genannt. Die bei der Verbindung von A Nukleonen zu
einem Atomkern
A
X
Z
freiwerdende Bindungsenergie EB ist dem
auftretenden Massendefekt ∆m proportional, und es gilt:
E B = ∆mc 2 .
(2.9)
Die Präzisionsbestimmung der Kernmassen mit Hilfe von hochauflösenden Massenspektrometern ermöglicht es, eine Systematik der
Kernbindungsenergien zu erstellen. In Abbildung 2.5 ist die mittlere
Bindungsenergie pro Nukleon E B / A als Funktion der Massenzahl
A dargestellt.
10
9
C-12
8
O-16
He-4
U-238
(Be-8)
7
E / A in MeV
B
Pb-208
Ni-60
Be-9
6
5
Li-6
4
3
He-3
2
H-2
1
H-1
0
40
80
120
160
200
240 A
Nukleonenzahl
Abb. 2.5: Bindungsenergie EB/A pro Nukleon in Abhängigkeit von
der Nukleonenzahl A
Die wichtigsten Ergebnisse lassen sich aus der Darstellung direkt
ablesen:
1.
Die mittlere Bindungsenergie pro Nukleon EB/A ist bei allen
Kernen gleich. Sie beträgt etwa 8 MeV.
59
2 Kernphysik
2.
Die größte Bindungsenergie weisen die Kerne im Massenbereich
zwischen A = 60 und A = 70 auf.
3.
Die Bindungsenergie nimmt nach kleineren Massenzahlen A
schnell und nach größerem A hin langsam ab
Die oben genannten experimentellen Befunde können bei Vernachlässigung von Feinheiten modellmäßig verstanden werden. Im Inneren eines Atomkerns erstreckt sich die Kernkraftwechselwirkung
jedes Nukleons wegen ihrer kurzen Reichweite nur auf die unmittelbaren Nachbarn. Das Verhalten der Nukleonen im Atomkern entspricht daher den Molekülen eines Flüssigkeitstropfens, die von der
kurzreichweitigen van-der-Waals-Kraft zusammen gehalten werden.
Soll ein Molekül verdampft werden, so muss gegen diese Anziehungskraft Arbeit geleistet werden, die von der Größe des Tropfens
unabhängig ist, solange Effekte der Oberflächenspannung vernachlässigt werden. Diese Verdampfungs- oder Kondensationswärme pro
Molekül entspricht die mittlere Bindungsenergie pro Nukleon im
Atomkern. Ein Atomkern verhält sich demnach analog zu einem
Flüssigkeitstropfen.
Zur theoretischen Beschreibung der Bindungsenergie der Atomkerne
liefert dieses Tröpfchenmodell somit:
E B ≈ aV ⋅ A .
Die Bindungsenergie wächst mit der Anzahl der Nukleonen. Sie ist
daher dem Kernvolumen proportional. Die empirisch zu ermittelnde
Konstante aV charakterisiert die Größe der Kernkraft. Bei kleinen
Flüssigkeitstropfen liegen viele Teilchen in der Oberflächenschicht
und sind somit nicht allseitig von Nachbarn umgeben. Sie sind daher
schwächer gebunden, ihre Bindungsenergie ist kleiner. Dieser Effekt
entspricht dem Einfluss der Oberflächenspannung auf die Verdampfungs- oder Kondensationswärme. Sie wird durch die gegen die
Oberflächenspannung zu verrichtende Oberflächenarbeit verringert.
Die Oberflächenenergie EF ist der Kernoberfläche O F proportional.
O F = 4πR K2
Mit R K = r0 A1 / 3 folgt: E F ∝ O F ∝ A 2 / 3
Die abzuziehende Oberflächenenergie liefert einen verbesserten Wert
für die Bindungsenergie der Atomkerne:
E B ≈ aV ⋅ A − a F ⋅ A 2 / 3
Die noch unbestimmte Konstante aF berücksichtigt hierbei die Stärke
des Oberflächeneffektes. Als weitere Korrektur muss schließlich die
60
2.2 Kernkraft und Bindungsenergie
Coulomb-Abstoßung der Protonen berücksichtigt werden. Nach dem
Coulombschen Gesetz wächst das elektrostatische Abstoßungspotential für eine Ladung proportional zur Gegenladung und umgekehrt
proportional zum Abstand r. Eine detaillierte Rechnung liefert für
die der Bindungsenergie entgegenstehende Coulomb-Energie E C :
EC ∝
Z 2e2
∝ Z 2 ⋅ A1 / 3
RK
E C = a C ⋅ Z 2 ⋅ A1 / 3
Sie muss aufgebracht werden, um ein freies Nukleonengas aus A
Nukleonen und Z Protonen zu einem Atomkern mit dem Kernradius
R K zu kondensieren. Die Konstante a C ist durch die CoulombWechselwirkung bestimmt. Damit erhält man für die Bindungsenergie der Atomkerne:
E B ≈ aV ⋅ A − a F ⋅ A 2 / 3 − a C ⋅ Z 2 ⋅ A1 / 3
(2.10)
Diese auf dem Tröpfchenmodell des Atomkerns basierende Formel
wurde 1935 von Carl Friedrich von Weizäcker und Hans Bethe aufgestellt und ist in der kernphysikalischen Literatur als BetheWeizäcker-Formel bekannt. Sie kann noch durch Berücksichtigung
zusätzlicher Terme zur Beschreibung von experimentellen Feinheiten
erweitert werden. Durch eine Präzisionsbestimmung der Kernmassen
lässt sich der Masseneffekt und damit die Kernbindungsenergie genau messen. Die Bethe-Weizäcker-Formel stellt eine semiempirische
Formel dar. Die in ihr enthaltenen Konstanten aV , a F und a C werden durch Anpassung der Bethe-Weizäcker-Formel an die experimentell bestimmten Bindungsenergien ermittelt.
Wird die Bindungsenergie E B durch die Nukleonenzahl A eines
Kerns geteilt, so erhält man die mittlere Bindungsenergie eines
Kerns pro Nukleon ( E B / A ). Durch die quadratische Abhängigkeit
der Bindungsenergie pro Nukleon von der Kernladungszahl Z nimmt
das Coulomb-Glied oberhalb von A ≈ 70 mit steigendem Z und A
stärker zu als das Oberflächenglied abnimmt. Für schwere Kerne A >
70 überwiegt daher der Einfluss der Coulomb-Energie, und die Bindungsenergie pro Nukleon nimmt infolgedessen mit wachsendem A
ab. Mit abnehmender Bindungsenergie werden die Atomkerne instabil, sodass bislang keine Atome mit Z > 118 beobachtet worden sind.
Aber auch für leichtere Atomkerne sind nicht alle Nukleonenkonfigurationen in natürlich vorkommenden Atomkernen realisiert. Das
Verhältnis von Neutronen zu Protonen (N/Z) liegt in stabilen leichten
Kernen etwa bei 1.
Beispiele:
4
He, 126 C, 168 O, 24
Mg, 40
Ca
2
12
20
61
2 Kernphysik
Dieses Verhältnis nimmt bei den schwersten Kernen bis zu Werten
von N / Z ≈ 1,6 zu. Schwere Atomkerne sind somit neutronenreicher.
Die elektrisch neutralen Neutronen verdünnen dabei die elektrische
Ladungsverteilung im Atomkern und mindern dadurch die durch
die Protonen hervorgerufene elektrische Abstoßung. Der schwerste
stabile Atomkern, der in der Natur vorkommt, gehört zu dem Reinelement Bismut
209
Bi .
83
Sein Verhältnis von Neutronen- zu Protonen-
zahl hat den Wert N/Z = 126/83 = 1,5. Noch schwerere in der Natur
vorkommende Atomkerne sind instabil (z. B.
238
U
92
mit dem Wert
N/Z = 146/92 = 1,59). Sie wandeln sich spontan durch radio-aktiven
Zerfall unter Emission von Teilchen- und Photonenstrahlung in
stabile Nuklide um.
2.3
Radioaktivität
Gegen Ende des 19. Jahrhunderts untersuchte Henri Becquerel Kristalle, die nach vorheriger Beleuchtung Licht aussandten. Diese Erscheinung wird Lumineszenz und Phosphoreszenz genannt. Die
Phosphoreszenz wird auch als Nachleuchten bezeichnet. Eines Tages
entdeckte er, dass uranhaltige Erze eine unbelichtete Fotoplatte, die
mit schwarzem Papier vollständig umwickelt war, geschwärzt hatten.
Es war bekannt, das diese Schwärzung auf einer Fotoplatte beispielsweise ein Maß für die Intensität einer Röntgen- oder UV-Strahlung
ist. Diese Beobachtung war die Geburtsstunde für die Entdeckung
der Radioaktivität. 1898 konnten Pierre und Marie Curie (1867 –
1934) aus dem Mineral Pechblende (U3O8) aus dem tschechischen
Uranbergwerk Joachimsthal zwei neue Elemente chemisch abtrennen. Sie nannten diese Radium (das Strahlende) und Polonium (nach
dem Heimatland von Marie Curie, nämlich Polen). In einer Vielzahl
von weiteren Versuchen konnten bis 1900 drei verschiedene Strahlungskomponenten in der „Uranstrahlung“ nachgewiesen werden.
Sie wurden mit kleinen griechischen Buchstaben als α-, β - und γStrahlung bezeichnet und lassen sich durch ihr unterschiedliches
Ablenkungsverhalten in einem magnetischen Feld charakterisieren
(Abb. 2.6).
Unter Radioaktivität (lat. radiare: strahlen) versteht man die Eigenschaft bestimmter radioaktiver Atome, der sog. Radionuklide, sich
spontan, d. h. ohne Einwirkung von außen unter Energieabgabe in
Form von ionisierender Strahlung in andere Atomkerne umwandeln.
Diese Kernumwandlung wird radioaktiver Zerfall genannt. Die
radioaktiven Atomkerne gehen dabei in einen energetisch stabileren
Zustand über. Unter ionisierender Strahlung versteht man eine
energiereiche Photonen- oder Teilchenstrahlung, die beim radioaktiven Zerfall emittiert wird und die beim Durchgang durch Materie
direkt oder indirekt die Bildung von Ionen bewirkt. Ursprung dieser
Strahlung ist der Atomkern. Sie wird deshalb auch Kernstrahlung
62
2.3 Radioaktivität
genannt. Die Radioaktivität ist daher eine Eigenschaft der Atomkerne. (Ionisierend wirkt aber auch die in der Elektronenhülle eines
Atoms infolge äußerer Anregung entstehende elektromagnetische
UV- und Röntgenstrahlung).
Magnetjoch
N
Radium
Magnetfeld
Kollimator
β
γ
α
Pb-Behälter
Leuchtschirm
S
Magnetjoch
Abb.2.6: Beim radioaktiven Zerfall auftretende Strahlungsarten
Beim radioaktiven Zerfall natürlicher Radionuklide können drei verschiedene Strahlenarten auftreten: α-, β - und γ-Strahlen. Da der
Mensch für keine dieser Strahlenarten ein Sinnesorgan besitzt, sind
für ihren Nachweis technische Messgeräte erforderlich. Die α- und
β-Strahlung ist eine Teilchenstrahlung, bei deren Freisetzung wandelt sich ein radioaktiver Atomkern eines Elements in einen Atomkern eines anderen Elements um.
Beim Alphazerfall wird aus dem Kern des radioaktiven Mutternuklids
A
M
Z
ein α-Teilchen genannter 42 He -Kern ausgestoßen. Dabei
wird eine Energie von 1 – 10 MeV frei, die als kinetische Energie
des emittierten α-Teilchens in Erscheinung tritt. Der Mutterkern M
wandelt sich dabei in einen Tochterkern T eines neuen Elements um.
Der α-Zerfall wird durch den 1. Verschiebungssatz von Rutherford
und Soddy beschrieben: Beim α-Zerfall nimmt die Nukleonenzahl A
um 4 und die Kernladungszahl Z um 2 Einheiten ab.
A
M
Z
→
A− 4
T
Z −2
+α .
(2.11)
Beispiel:
238
U
92
→
234
Th + 42 He
90
+ 4,18 MeV
63
2 Kernphysik
Beim Betazerfall wandelt sich im Atomkern ein Neutron in ein Proton und ein Elektron um.
n → p + e +ν e
(2.12)
Dabei entsteht ein weiteres neutrales Elementarteilchen, das sog.
Elektronenantineutrino ν e , das jedoch mit Materie kaum in Wechselwirkung tritt und daher hier vernachlässigt werden kann. Das ausgesandte Elektron wurde ursprünglich als β−Teilchen bezeichnet. Es
verlässt den Atomkern, während das Proton zurückbleibt. Dieser
Sachverhalt wird durch den 2. Verschiebungssatz von Rutherford und
Soddy beschrieben: Beim β−Zerfall bleibt die Nukleonenzahl A konstant, die Kernladungszahl Z nimmt um eine Einheit zu.
A
M
Z
→
A
T
Z +1
→
3
He
2
+ e +ν e
(2.13)
Beispiel:
3
H
1
+ e + ν e + 35 eV
Freie Neutronen sind instabile Teilchen und zerfallen nach Gl. 2.12
mit einer Halbwertszeit von etwa 10 min. Im Gegensatz dazu sind
freie Protonen und Elektronen stabil. Bislang wurde noch kein Zerfall von freien Protonen beobachtet. Nach neuesten Messungen ist
ihre Halbwertszeit größer als 1033Jahre.
Der Gammazerfall ist eine Begleiterscheinung fast aller radioaktiven α− und β−Zerfälle. Die Nukleonen im Atomkern können wie die
Elektronen in der Atomhülle in Bezug auf den Grundzustand angeregte Zustände annehmen. Aus solchen angeregten Kernniveaus mit
Energien unterhalb der Teilchenemissionsschwelle sind nur Gammazerfälle möglich. Die dabei auftretende γ−Strahlung besteht aus
hochenergetischen elektromagnetischen Quanten, die keine Ruhemasse besitzen. Die γ−Strahlung besitzt keinen korpuskularen Charakter, sie ist keine Teilchenstrahlung. Die durch Kernumwandlung
entstandenen Tochterkerne T * können überschüssige Anregungsenergie durch die Emission einer energiereichen Photonenstrahlung,
der so genannten γ−Quanten, abgeben. Sie gehen dabei ohne Kernumwandlung unter Abgabe von Energie in Form der γ−Strahlung in
ihren stabilen Grundzustand T über.
A *
T
Z
64
→
A
T
Z
+γ
(2.14)
2.3 Radioaktivität
2.3.1
Das radioaktive Zerfallsgesetz
Der radioaktive Zerfall von Atomkernen ist ein statistischer Prozess.
Die Zahl der Kerne einer radioaktiven Substanz nimmt dabei exponentiell ab:
N (t ) = N 0 e − λt .
(2.15)
λ ist eine stoffspezifische Zerfallskonstante des betreffenden Nuklids, N0 ist die Anzahl der zum Anfangszeitpunkt t = 0 vorhandenen
radioaktiven Atome. Die Halbwertszeit T1/2 ist die Zeitspanne, in der
die Anzahl der radioaktiven Atome durch Zerfall auf die Hälfte des
Ausgangswertes abnimmt. Es gilt:
T1 =
2
ln 2
(2.16)
λ
Anzahl
N
0
N /2
0
0
0
1
2
3
t
T
1/
2
Abb. 2.7: Radioaktiver Zerfall und Halbwertszeit
Unter der Aktivität eines Radionuklids versteht man die Anzahl dN
der spontanen Zerfälle im Zeitintervall dt.
A(t ) = −
dN
= λ ⋅ N (t ) = λ ⋅ N 0 ⋅ e −λ ⋅t = A0 ⋅ e −λ ⋅t
dt
(2.17)
Mit Hilfe der Aktivität kann die Halbwertszeit als dasjenige Zeitintervall interpretiert werden, in dem die Aktivität eines Radionuklids
durch radioaktiven Zerfall auf die Hälfte abfällt.
Die Zerfallskonstante λ stellt statistisch gesehen die Wahrscheinlichkeit dar, dass ein radioaktiver Kern in einem beliebigen Zeitintervall
dt zerfällt. Bei einem Ensemble von N radioaktiven Kernen addieren
sich die Einzelwahrscheinlichkeiten für den Zerfall im Zeitintervall
dt. Die Anzahl dN der zu erwartenden Zerfälle ist dann gegeben
durch:
65
2 Kernphysik
dN = − N ⋅ λ ⋅ dt
Das Minuszeichen berücksichtigt die Tatsache, dass durch die Anzahl dN der Zerfälle die Zahl N der verbliebenen radioaktiven Kerne
abnimmt.
Die Aktivität A einer radioaktiven Substanz wird daher als Anzahl
∆N der in einem Zeitintervall auftretenden Kernumwandlungsprozesse eines Radionuklids dividiert durch die Länge ∆t des Zeitintervalls definiert.
A=
∆N
∆t
(2.18)
Die Aktivität stellt somit eine Zerfallsrate dar, die auch mit N& bezeichnet wird. Jeder radioaktive Zerfallsprozess infolge der Emission
eines α− oder β− Teilchens führt zu einer solchen Kernumwandlung.
Die SI-Einheit für die Aktivität ist das Becquerel (Bq). Der Name
der Einheit für die Aktivität leitet sich von Antoine Henri Becquerel
(1852 – 1908), dem Entdecker der Radioaktivität, ab.
1
[ A] = = 1 Bq
s
(2.19)
Die Aktivität von 1 Bq entspricht einen radioaktiven Zerfallsprozess
pro Sekunde (1 Bq = 1 s–1).
Die früher gebräuchliche und bis Ende 1984 amtlich noch zugelassene Einheit der Aktivität war das Curie mit dem Einheitenzeichen Ci.
1 Ci = 3,7 ⋅ 1010 Bq
Die Aktivität von 1g Radium (A = 226) beträgt ungefähr 1 Ci. Genaue Messungen ergeben eine Aktivität von 0,989 Ci.
Beispiele:
a) Radium(A = 226) zerfällt unter α−Emission in Radon
(A = 222).
Ra − 226 → Rn − 222 + α
Werden von einem Radiumpräparat pro Minute 600 α−Teilchen
emittiert, so folgt für die Aktivität des Präparates:
A = 600 Zerfälle / 1 min = 10 Zerfälle / 1 s = 10 Bq
66
2.3 Radioaktivität
b) Iridium (A = 192) zerfällt unter β−Emission in Platin (A = 192).
Ir − 192 → Pt − 192 + β −
Werden von einem Iridiumpräparat pro Stunde 3,6 Millionen
Elektronen emittiert, so folgt für die Aktivität des Präparates
A = 3,6 ⋅ 10 6 Zerfälle / 1 h = 3,6 ⋅ 10 6 Zerfälle / 3600 s = 1000 Bq
Unter der spezifischen Aktivität a einer radioaktiven Substanz versteht man den Quotienten aus ihrer Aktivität A und ihrer Masse m:
2.3.2
a=
A
m
(2.20)
[a] =
Bq
kg
(2.21)
Radioaktive Umwandlungsreihen
Die beim radioaktiven Zerfall von schweren Atomkernen entstehenden Tochterkerne sind meist wieder radioaktiv und zerfallen ebenfalls mit nuklidspezifischen Halbwertszeiten. Auf diese Weise entstehen radioaktive Umwandlungsreihen, die schließlich bei einem
stabilen Element enden. Es sind vier solcher Umwandlungsreihen
bekannt. Drei Umwandlungsreihen gehen von natürlich vorkommenden radioaktiven Ausgangskernen aus: Uran-Radium-Reihe, UranAktinium-Reihe und Thorium-Reihe. Die vierte Reihe beginnt mit
dem künstlich hergestellten Element Neptunium.
Name der Reihe
Ausgangskern
Stabiler Endkern
Halbwertszeit
Uran-Radium
238
U
92
206
Pb
82
4,5 ⋅ 10 9 a
Uran-Aktinium
235
U
92
207
Pb
82
0,7 ⋅ 10 9 a
Thorium
232
Th
90
208
Pb
82
14 ⋅ 10 9 a
Neptunium
237
Np
93
209
Bi
83
2,1 ⋅ 10 6 a
Tabelle 2.1: Radioaktive Umwandlungsreihen
Entsprechend den Verschiebungssätzen von Rutherford und Soddy
lassen sich die Umwandlungsreihen in einer Nuklidkarte in Form
eines N-Z-Diagramms graphisch darstellen. Jedes Nuklid ist in dieser
Darstellung eindeutig durch seine Neutronen- und Protonenzahl cha-
67
2 Kernphysik
rakterisiert. Damit ist auch die Massenzahl A = N + Z eines jeden
Nuklids festgelegt. In der Nuklidkarte ist die Neutronenzahl N als
Ordinate und die Ordnungszahl Z als Abszisse aufgetragen. Die
β-Zerfälle sind durch kurze nach rechts gerichtete Pfeile markiert.
Die α-Zerfälle sind durch nach links gerichtete längere Pfeile dargestellt. Einige Nuklide besitzen zwei alternative Zerfallswege. Sie
können sich entweder durch α-Zerfall oder durch β -Zerfall umwandeln. Dadurch entstehen mehrere Verzweigungsmöglichkeiten entlang der Zerfallsreihe. Die folgende Abbildung zeigt dies am Beispiel der Uran-Radium-Reihe.
N
U-235
Th-231
Pa-231
140
Ac-227
Th227
Fr-223
Ra223
135
At-219
α-Zerfall
Rn-219
Bi-215
–
β -Zerfall
Po-215
At215
130
Pb-211
Bi-211
Po-211
Ti-207
Pb-207
125
75
80
85
90
95
Z
Abb. 2.8: Natürliche radioaktive Umwandlungsreihe
2.4
Kernreaktionen
Kernreaktionen sind Umwandlungen von Atomkernen, die durch
Wechselwirkung mit Elementarteilchen oder anderen Atomkernen
ausgelöst werden. Voraussetzung für eine Kernreaktion ist es, dass
ein Elementarteilchen dicht an einen Atomkern gelangt. Dazu werden in der Regel ruhende Zielkerne, die man auch als Targetkerne
bezeichnet, mit Geschossteilchen bombardiert. Positiv geladene
Geschossteilchen wie Protonen oder α-Teilchen benötigen dazu eine
beträchtliche kinetische Energie; sie müssen nämlich zunächst die
abstoßende Coulombkraft überwinden, um in den Wirkungsbereich
der kurzreichweitigen Kernkraft zu gelangen. Dazu kann die Energie
des radioaktiven Zerfalls ausgenutzt werden (Beispiel: α-Teilchen),
oder die Geschossteilchen müssen in komplizierten Anlagen, den
sog. Teilchenbeschleunigern, auf hohe kinetische Energien gebracht
68
2.4 Kernreaktionen
werden. In symbolischer Schreibweise wird eine Kernreaktion durch
die folgende Reaktionsgleichung dargestellt:
x + X → Y+ y
(2.22)
In der Kernphysik hat sich dafür die Schreibweise
X(x,y)Y
(2.23)
eingebürgert. Dabei stellt X den mit dem Targetkern identischen
Eingangskern dar, x beschreibt das einlaufende Geschossteilchen,
Y repräsentiert den bei der Kernreaktion entstehenden Folgekern und
y stellt das auslaufende Teilchen dar.
Bei allen Kernreaktionen ändern sich bestimmte physikalische Größen wie Gesamtimpuls, Gesamtenergie, Gesamtladung und Nukleonenzahl aller beteiligten Teilchen nicht. Sie bleiben vielmehr erhalten. Für diese Größen gelten somit Erhaltungssätze. Der Erhaltungssatz für die Nukleonenzahl besagt beispielsweise:
Die Summe der Nukleonenzahlen von Targetkern X und
Geschossteilchen x vor der Kernreaktion ist gleich der
Summe der Nukleonenzahlen von Folgekern Y und auslaufenden Teilchen y nach der Kernreaktion.
1932 hatte Chadwick beim Beschuss einer Beryllium-Folie mit
α-Teilchen Neutronen in folgender Kernreaktion entdeckt:
4
He
2
+
9
Be
4
→
12
C
6
+
1
n
0
(2.24)
Der Erhaltungssatz für die Nukleonenzahl lautet: 4 + 9 = 12 +1.
Auch heute werden noch Radium-Beryllium-Gemische als Neutronenquellen verwendet. Die kosmogenen Radionuklide 31 H (Tritium)
und
14
C
6
(Radiokohlenstoff) werden durch Kernreaktionen zwischen
der kosmischen Strahlung und den Gasatomen der Erdatmosphäre
ständig neu gebildet. Die kosmische Strahlung besteht hauptsächlich
aus hochenergetischen Protonen. Bei ihrer Abbremsung in den obersten Schichten der Atmosphäre entstehen als sekundäre Reaktionsprodukte Neutronen. Diese bilden in Kernreaktionen mit dem Stickstoff der Luft die kosmogenen Radionuklide:
1
n
0
+
14
N
7
→
12
C
6
+
3
H
1
(2.25)
1
n
0
+
14
N
7
→
14
C
6
+
1
H.
1
(2.26)
69
2 Kernphysik
Auch der Ausgangskern der Neptunium-Reihe, nämlich das Nuklid
237
Np
93
entsteht beispielsweise aus
235
U
92
durch Neutronenbeschuss.
Die kernphysikalische Reaktionsgleichung dieser (n, γ)-Reaktion
lautet:
1
n
0
+
235
U
92
→
236
U
92
+ γ
(2.27)
1
n
0
+
236
U
92
→
237
U
92
+ γ
(2.28)
Durch β -Zerfall erhält man:
237
U
92
→
237
Np
93
+ e−
(2.29)
Zum Neutronennachweis wird die folgende Kernreaktion ausgenutzt:
1
n
0
+
10
B
5
→
7
Li
3
+
4
He
2
(2.30)
In der experimentellen Messtechnik wird dazu dem Zählgas
beispielsweise eines Geiger-Müller-Zählrohres gasförmiges
Bortrifluorid (BF3) zugesetzt.
Auch das Transuran Plutonium Pu-239 verdankt sein Vorkommen
einer (n,γ)-Reaktion:
1
n
0
238
U
92
+
Das radioaktive Isotop
239
U
92
→
239
U
92
+ γ
(2.31)
ist ein Betastrahler, das sich durch zwei
sukzessive β -Zerfälle in Plutonium umwandelt.
239
U
92
239
Np
93
T 

→
= 23,5 min
239
Np
93
+ e−
(2.32)
T 
→
= 2,35 d
239
Pu
94
+ e−
(2.33)
12
12
Neutronen können als ungeladene Teilchen die Atome praktisch
ungehindert durchdringen. Sie erfahren auch keine Coulombsche
Abstoßungskraft durch die Atomkerne, wohl aber die anziehende
Kernkraft. Sie werden infolgedessen im Atomkern absorbiert und
eingelagert, wobei ihre Bindungsenergie in Form von γ-Strahlung
abgegeben wird. Ein solcher Neutroneneinfang wird als (n,α)Reaktion bezeichnet. Neutroneneinfang-Reaktionen sind für den
Aufbau von schweren Elementen aus leichten Elementen in Form der
so genannten Elementsynthese in den Sternen von Bedeutung. Als
Beispiel sei dazu die folgende Reaktion betrachtet:
70
2.5 Kernspaltung und Kernfusion
1
n
0
+
31
P
15
→
32
P
15
(2.34)
+ γ
Das radioaktive Phosphor-32 wandelt sich in das stabile Schwefel-32
um:
32
P
15
→
32
S
16
+ e−
(2.35)
Aus dem leichteren Nuklid Phosphor-31 ist ein Nuklid des schwereren Elements Schwefel entstanden. Entsteht durch Neutroneneinfang
ein radioaktives Isotop des Ausgangsnuklids, so kann dessen ionisierende Strahlung zum eindeutigen Nachweis des Ausgangsnuklids
verwendet werden. Das dabei eingesetzte Verfahren wird Neutronenaktivierungsanalyse genannt.
Die Neutronenaktivierungsanalyse ist eine Methode zur qualitativen
und quantitativen Bestimmung von Elementen in festen, flüssigen
und gasförmigen Substanzproben. Von besonderer Bedeutung ist
dabei, dass der Nachweis unabhängig vom chemischen Zustand ist,
in dem sich das gesuchte Element befindet. Die Methode wird insbesondere im Bereich der Spurenanalyse von Elementen eingesetzt.
Sie beruht auf der genauen Kenntnis der Kernreaktionen, die durch
Neutronen ausgelöst werden. Auf einer neutroneninduzierten Kernreaktion beruht auch die im nächsten Abschnitt beschriebene Kernspaltung.
2.5
Kernspaltung und Kernfusion
1939 entdeckte Otto Hahn (1879 – 1968) zusammen mit seinen
Mitarbeitern Fritz Straßmann (1902 – 1980) und Lise Meitner
(1878 – 1968), dass sich bei der Bestrahlung von Uran mit Neutronen leichtere Elemente aus der Mitte des Periodensystems bilden.
Dieses Ergebnis kennzeichnet die Entdeckung eines neuen Typs von
Kernreaktionen, den Kernspaltungsreaktionen. Bei der Kernspaltung wird unter Neutronenbeschuss ein schwerer Kern in zwei leichtere Kerne zerlegt, die als Spaltprodukte bezeichnet werden. Die
Kernspaltung wird dabei durch das Auftreten von 2 bis 3 freien
Neutronen, den sog. Spaltneutronen, begleitet. Während in leichten
Atomkernen das Verhältnis von Neutronen zu Protonen ungefähr
gleich
ist (N/Z ≈ 1), sind schwere Kerne reich an Neutronen. Bei der Kernspaltung treten somit überzählige Neutronen auf.
In der folgenden Reaktionsgleichung sind zwei mögliche Beispiele
für die Spaltung von Uran-235 angegeben:
1
n
0
+
235
U
92
→
236 *
U
92
→
139
Xe
54
+
95
Sr
38
+ 2 01 n
(2.36)
71
2 Kernphysik
1
n
0
+
235
U
92
→
236 *
U
92
→
140
Ba
56
+
93
Kr
36
+ 3 01 n
(2.37)
Die Kernspaltungsreaktion läuft über einen angeregten Zwischenkern
236 *
U ,
92
der auch als Compoundkern bezeichnet wird. Sie kann im
Rahmen des in Abschnitt 2.2 dargestellten Tröpfchenmodells interpretiert werden. Gemäß Abb. 2.4 beträgt die mittlere Bindungsenergie pro Nukleon für Uran-235 etwa 7,5 MeV.
Abb. 2.9: Kernspaltung von Uran
Die bei der Kernspaltung entstehenden Spaltprodukte wie beispielsweise Barium-140 oder Krypton-93 haben eine größere Bindungsenergie pro Nukleon, nämlich etwa 8,4 MeV. Pro Uran-235-Nukleon
werden daher bei der Spaltung etwa 0,9 MeV an Bindungsenergie
frei. Im statistischen Mittel über viele Spaltungsprozesse von Uran235 werden entsprechend pro gespaltenem Uran-235 ca. 200 MeV
und 2,5 Neutronen frei. Bei der Kernspaltung wird somit pro Elementarprozess eine Energie freigesetzt, welche die bei exothermen
chemischen Reaktionen abgegebene Energie um den Faktor 106
übertrifft. Diese Energie tritt als kinetische Energie der Spaltprodukte auf. Die Spaltprodukte sind immer noch neutronenreich und daher
radioaktiv. Sie verwandeln sich infolge von β−Zerfall durch Elektronenemission in stabile Kerne um. Die Kernspaltung setzt, wie in
Abb. 2.9 gezeigt, eine Deformation des zu spaltenden Kerns voraus.
Dazu muss eine Deformationsenergie aufgebracht werden, die als
Aktivierungsenergie bezeichnet wird. Diese Aktivierungsenergie
wird dem Urankern durch die kinetische Energie des Neutrons und
durch die frei werdende Bindungsenergie des Neutrons bei seiner
Anlagerung zugeführt. Diese Aktivierungsenergie stellt eine Art
Spaltbarriere dar; sie hat für Uran-235 eine Größe von 6,1 MeV.
Andererseits ergibt eine genaue Analyse, dass bei der Anlagerung
eines Neutrons an den Uran-235-Kern eine Bindungsenergie von
6,5 MeV frei wird. Durch diese Anlagerungsenergie kann daher
die Uran-235-Spaltung aktiviert werden, ohne dass es dazu einer
zusätzlichen kinetischen Energie des Neutrons bedarf. Um dagegen
einen Uran-238-Kern zu spalten, müsste das Neutron zusätzlich noch
eine kinetische Energie von 2,2 MeV besitzen, denn seine Anlagerungsenergie beträgt nur 4,8 MeV. Uran-235 kann somit durch langsame Neutronen gespalten werden; diese werden als thermisch bezeichnet. Genauere Untersuchungen zeigen, dass die Wahrscheinlichkeit σ f für eine neutroneninduzierte Spaltung von Uran-235 mit
72
2.5 Kernspaltung und Kernfusion
zunehmender kinetischer Neutronenenergie En abnimmt. Dabei gilt
die Proportionalität
1
σf ∝
.
(2.38)
En
Die Spaltwahrscheinlichkeit σ f ist für thermische Neutronen besonders groß. Die bei der Kernspaltung frei werdenden Neutronen
können neue Spaltprozesse hervorrufen. Dadurch wird eine Kettenreaktion möglich. Die Neutronenbilanz wird durch einen NeutronenVermehrungsfaktor k beschrieben, d. h. durch das Verhältnis der
Anzahl der Neutronen in einer gegebenen Generation zu ihrer Anzahl in der vorangegangenen Generation. Als notwendige Bedingung
für das Auftreten einer Kettenreaktion gilt: k ≥ 1 . Für k = 1 kann eine
stationäre Kettenreaktion aufrechterhalten werden. In diesem Fall
muss im Mittel von den bei der Uran-235-Spaltung frei werdenden
2,5 Neutronen genau eines wieder zur Spaltung führen. Die Uran235-Masse einer solchen Anordnung mit k = 1 heißt kritische Masse.
Ist dagegen die Masse des Spaltmaterials zu klein, so entweichen im
Mittel mehr als 1,5 Neutronen von den pro Spaltprozess freigesetzten
2,5 Neutronen. Die Kettenreaktion kann dann nicht aufrechterhalten
werden und kommt zum Erliegen.
Technische Anlagen, in denen durch gesteuerte Kettenreaktionen
Energie durch Kernspaltung bereitgestellt wird, heißen Kernreaktoren. Technisch sind zwei Reaktortypen gebräuchlich: Siedewasserreaktor und Druckwasserreaktor. Der Siedewasserreaktor arbeitet im
Prinzip wie ein Tauchsieder. Infolge der bei der Kernspaltung freigesetzten Kernenergie, erhitzen sich die Brennstäbe. Das vorbeiströmende Wasser erwärmt sich, beginnt zu sieden und geht dabei teilweise in den Dampfzustand über. Die Dampftemperatur beträgt dabei etwa 290° C, der Druck des Dampfes ungefähr 70 bar.
Antriebe für
Steuerstäbe
Turbine
Generator
Dampf
G
Steuerstäbe
320°C
Brennelemente
290°C
Kühlwasser
1
Wasser
Reaktordruckgefäß
Wärmetauscher
und
Dampferzeuger
Primärkreislauf
Wasser
Kondensator
2
Sekundärkreislauf
Abb. 2.10: Druckwasserreaktor in schematischer Darstellung
Der Druckwasserreaktor (Abb.2.10) besteht aus zwei geschlossenen
Kreisläufen: Primär- und Sekundärkreislauf. Im Primärkreislauf
73
2 Kernphysik
herrscht ein großer Druck von etwa 150 bar. Dadurch erhöht sich
die Siedetemperatur des Wassers beträchtlich, sodass es selbst bei
Temperaturen von etwa 320° C im flüssigen Zustand bleibt. Das
hoch erhitzte Wasser durchfließt dann einen Wärmetauscher, in dem
Wasser verdampft wird. Der Wärmetauscher gehört zum Sekundärkreislauf und stellt zugleich auch einen Dampferzeuger dar. Der
Hochdruck-Wasserdampf (T ≈ 270 °C, p ≈ 50 bar) durchströmt dann
eine direkt angeschlossene Turbine. Dabei entspannt er sich und
kühlt ab. Im Kondensator wird der Dampf dann mit Hilfe von Speisewasser weiter abgekühlt und verflüssigt.
Die erste gesteuerte Kettenreaktion wurde 1942 von Enrico Fermi in
einer reaktorähnlichen Anordnung an der Universität von Chicago
verwirklicht. Wesentliche Elemente eines modernen Kernreaktors
zur Nutzung der Kernenergie sind: Brennstäbe, Moderator, Steuerstäbe und Wärmeträgermedium. Als Kernbrennstoffe werden die
spaltbaren Nuklide Uran-235 oder Plutonium-239 in keramischer
Form als UO2 oder PuO2 verwendet. Als Steuerstäbe werden neutronenabsorbierende Substanzen wie die Metalle Bor (B) und Cadmium
(Cd) eingesetzt. Werden die Steuerstäbe in den Reaktorkern gefahren, so geht der Neutronenvermehrungsfaktor k gegen Null, und die
Kettenreaktion bricht ab. Die Spaltneutronen haben im Mittel eine
kinetische Energie von 2 MeV. Die kritische Masse des Reaktors
kann reduziert werden, wenn man vorwiegend nur möglichst langsame Neutronen zur Spaltungsreaktion bringt. Die Neutronen werden
dazu durch Stöße mit einer Substanz abgebremst oder moderiert. Als
Moderator wird Wasser eingesetzt, welches gleichzeitig als Kühlmittel dient. Durch die Abbremsung der Spaltprodukte erhitzen sich die
Brennstäbe. Durch Wärmeübertragung geben sie diese Energie an
das durch den Reaktorkern strömende Wasser ab. Ein Kernkraftwerk
unterscheidet sich von einem kohlebefeuerten konventionellen
Kraftwerk hauptsächlich durch die Art der Wärmeerzeugung.
Neben der Kernspaltung kann auch durch die Fusionsreaktion leichter Atomkerne Energie gewonnen werden. Die Kernfusion genannte
Verschmelzung von leichten Atomkernen stellt die Energiequelle der
Sterne dar. Unsere Sonne ist somit ein großer thermonuklearer Fusionsreaktor, bei dem Wasserstoff zu Helium verschmolzen wird. Der
wichtigste Reaktionspfad bei der Energiegewinnung der Sonne ist
der Wasserstoff-Zyklus, auch als Proton-Proton-Zyklus bezeichnet.
Er wird durch die folgenden Reaktionsgleichungen beschrieben:
1
1p
+ 11p → 21H +
1
1p
0
+1 e + ν e
(2.39a)
+ 0,42 MeV
+ 21H → 32 He + γ + 5,49 MeV
(2.39b)
3
2 He
(2.39c)
+
3
2 He
→
4
2 He
+ 2
1
1p + 12,9 MeV
In dieser Schreibweise wird durch das Symbol
0
e
+1
das so genannte
Antiteilchen des Elektrons gekennzeichnet. Es wird Positron genannt
74
2.5 Kernspaltung und Kernfusion
und stellt ein elektrisch positiv geladenes Elektron dar. Das Positron
ist – wie das Elektron – ein leichtes Elementarteilchen; beide gehören zur Klasse der Leptonen und besitzen die Nukleonenzahl Null.
Die zur Fusion notwendige kinetische Energie erlangen die Protonen
( 11 p ) aufgrund ihrer Wärmebewegung infolge der hohen SonnenTemperatur. Die für die Sonnenenergieproduktion wesentliche Fusionsreaktion (2.39a), der Proton-Proton-Zyklus, wird auch in der
Form p + p → d + e + + ν e angegeben. Diese Reaktion basiert auf der
schwachen Wechselwirkung, bei der ein Proton in ein Neutron
umgewandelt wird und zusammen mit dem anderen Proton einen
schweren Wasserstoffkern bildet. Die Fusionsreaktion (2.39a) verläuft über den quantenmechanischen Tunneleffekt und besitzt daher
eine geringe Reaktionsrate. ν e ist dabei ein elektrisch neutrales Elementarteilchen mit äußerst geringer Masse, welches Neutrino genannt wird. Mit d wird der Atomkern des schweren Wasserstoffisotops Deuterium abgekürzt, für den der kernphysikalische Name Deuteron eingeführt wurde.
Mit der Entdeckung der Kernspaltung begann ein neues Zeitalter. Es
ist gekennzeichnet durch die Entwicklung von Kernwaffen und einen
nuklearen Rüstungswettlauf, der die zweite Hälfte des 20. Jahrhunderts geprägt hat. Der Eintritt in das Atomzeitalter wurde der Weltöffentlichkeit erst am 06. August 1945 bewusst, als ein Atombombenabwurf über der japanischen Stadt Hiroshima unmittelbar 70000
Menschen tötete. Nach 5 Jahren wurden insgesamt 200000 Opfer
registriert.
Abb. 2.11: Atombombenangriff auf Hiroshima: „Als wär die Sonne
vom Himmel gefallen“
75
2 Kernphysik
Die erste künstliche Kernfusionsreaktion wurde 1953 bei der Explosion einer Wasserstoffbombe realisiert, die als Sprengstoff ein Gemisch aus Deuterium und Tritium enthielt. Eine Fusionsreaktion ist
nur möglich, wenn sich die beiden Atomkerne sehr dicht annähern.
Erst bei Abständen r ≈ RK wirkt die anziehende Kernkraft. Für diese
Annäherung ist eine kinetische Energie notwendig, die ausreicht, um
die elektrische Coulomb-Abstoßung zu überwinden (Abb. 2.12). Die
Abbildung zeigt die potentielle Wechselwirkungsenergie E als Funktion des Teilchenabstandes r zwischen den beiden Atomkernen. Der
Tritiumatomkern ist dabei als ein Potentialtopf dargestellt, der von
einem abstoßenden Coulomb-Wall der Höhe EC umgeben ist.
Coulomb-Potential
E
d
E
R
K
R
0
E
k in
C
r
K
E
A
B
t
Kernpotential
Abb. 2.12: Potentialtopf-Modell der Atomkerne
Untersuchungen zur kontrollierten Kernfusion werden seit vielen
Jahren durchgeführt. Für die Überwindung der Coulomb-Abstoßung
sind kinetische Energien zwischen 104 und 105 eV erforderlich. Dies
entspricht Temperaturen von 108 bis 109 K. Dazu werden in Fusionsreaktoren geeignete Brennstoffe bei extrem hohen Temperaturen in
starken Magnetfeldern komprimiert. Bei diesen hohen Temperaturen
haben die Atome alle ihre Elektronen abgegeben und liegen im vollständig ionisierten Zustand vor. Dieser Zustand wird als Plasmazustand bezeichnet. Das extrem heiße Fusionsplasma darf nicht in
Kontakt mit den materiellen Wänden des Fusionsreaktors kommen.
Dies wird durch den so genannten magnetischen Einschluss mit Hilfe
starker Magnetfelder erreicht. Die Magnetfelder üben dabei auf die
bewegten elektrisch geladenen Teilchen des Plasmas eine Kraft aus.
Die beiden wichtigsten thermonuklearen Reaktionen mit den dabei
frei gesetzten Energien werden in den folgenden Reaktionsgleichungen zusammenfassend dargestellt:
2
d
1
76
+
2
d
1
→
3
He
2
+
1
n
0
+ γ + 3,2 MeV
(2.40)
2.5 Kernspaltung und Kernfusion
3
t
1
+
2
d
1
→
4
He
2
+
1
n
0
+ γ + 17,6 MeV
(2.41)
Der Atomkern des schweren Wasserstoffs ( 21 H ) wird Deuteron (d)
und der des überschweren Wasserstoffs ( 31 H ) wird Triton (t)
genannt. Der Tritiumkern (t) entsteht dabei in einer exothermen
Reaktion, z. B. aus dem Lithium durch die Kernreaktion:
6
3 Li
+ 01n → 73 Li * → 42 He +
3
1t
+ γ + 4,67 MeV
(2.42a)
In den Reaktionen (2.40) und (2.41) entstehen energiereiche freie
Neutronen n, die durch Neutronenaktivierung zur radioaktiven Kontaminierung der Reaktormaterialien beitragen können. Neuerdings
werden daher auch neutronenfreie Kernfusionsreaktionen diskutiert:
11
4B
+ 11H → [125 Be] * → 3 42 He + 8,7 MeV
(2.42b)
Die kernphysikalische Realisierung von kontrollierten Fusionsreaktionen konnte inzwischen durch den Nachweis von bei diesen Reaktionen entstehenden Neutronen experimentell belegt werden. Die derzeitigen Fusionsreaktoren haben allerdings noch eine negative Energiebilanz. Sie geben sehr viel weniger Energie ab, als ihnen von außen zur Aufrechterhaltung der Kernverschmelzung zugeführt werden
muss. Die technische Machbarkeit der Energiegewinnung durch
Kernfusion soll durch den Bau eines Internationalen Thermonuklearen Experimental-Reaktors (ITER) im südfranzösischen Cadarache
demonstriert werden. Es handelt sich dabei um ein Fusionskraftwerk
mit magnetischem Einschluss des Brennstoffplasmas in einer als
Tokamak bezeichneten toroidalen Konfiguration. Die Idee des ITERProjektes geht auf das Jahr 1985 zurück. Die Kostenschätzung aus
dem Jahr 2000 ging von 5 Mrd. € aus und der Reaktor sollte 2018
voll einsatzbereit sein. Inzwischen (Stand: 2015) werden Kosten von
16 Mrd. € genannt und mit der Inbetriebnahme wird frühestens 2025
gerechnet. Ein alternatives Fusionsreaktorkonzept wird vom MaxPlanck-Institut für Plasmaphysik in Greifswald realisiert. Es handelt
sich um einen Stellarator, der als Wendelstein 7-X bezeichnet wird
und sich zurzeit in der Testphase befindet. Ziel ist es, für einige
Minuten eine Plasmatemperatur von 100 Millionen Grad Celsius zu
erreichen.
Durch die Kernverschmelzung schwerer Atomkerne können Elemente jenseits des Urans künstlich hergestellt werden. Sie werden Transurane genannt. Dabei werden schwere Ionen wie beispielsweise
Zirkoniumionen in Teilchenbeschleunigern mit Hilfe elektrischer
Felder auf hohe kinetische Energien beschleunigt und auf dünne
Bleifolien (Pb-Targets) geschossen. 1974 wurde mit Hilfe solcher
Fusionsreaktionen das Element Rutherfordium (Z = 106) erzeugt.
1996 konnte bei der Gesellschaft für Schwerionenforschung (GSI) in
77
2 Kernphysik
Darmstadt das Element Copernicium (Z = 112 (Cn)) nachgewiesen
werden, welches 2009 von der IUPAC offiziell als entdeckt anerkannt wurde. Die ebenfalls dort synthetisierten Elemente Z = 108
(Hs) und Z = 110 (Ds) wurden deshalb durch die International Union für Pure and Applied Chemistry (IUPAC) Hassium (nach dem
Bundesland Hessen) und Darmstadtium genannt. Als sicher erzeugt
und durch ihre Zerfallsketten nachgewiesen gelten zurzeit (2016) die
Elemente mit Z = 114 (Flerovium (Fv)) und Z = 116 (Livermorium
(Lv)) sowie die noch namenslosen Elemente Z = 113, Z = 115, Z =
117 und Z = 118. Es handelt sich dabei um radioaktive Isotope mit
kurzer Halbwertszeit (T1/2 ≈ 1 ms), die in der Natur nicht vorkommen. Für Kernphysiker stellt sich zurzeit die wichtige Frage: Gibt es
eine Insel der Stabilität, dass heißt einen Bereich auf der Nuklidkarte, in dem langlebige oder gar stabile superschwere Elemente existieren können?
2.6
Wechselwirkung ionisierender Strahlung mit
Materie
Die wichtigsten Wechselwirkungsprozesse von α- und β-Teilchen
mit Materie sind elastische Stöße, bei denen kinetische Energie auf
die atomaren Stoßpartner übertragen wird und unelastische Stöße,
die zur Anregung und Ionisation der Atome des durchstrahlten Mediums führen. Dabei werden Elektronen auf höhere Bahnen gehoben
oder vollständig vom Atom getrennt. Die α- oder β -Teilchen geben
dabei Energie ab und werden abgebremst. Sie besitzen in Materie
nur eine begrenzte Reichweite, die umso größer ist, je größer die
Teilchenenergie und je kleiner die Dichte des Absorbermaterials ist.
Im Gegensatz zu elektrisch geladenen Teilchen ist Gammastrahlung
nur indirekt ionisierend. Durch Photoeffekt und Comptonstreuung
wird die elektromagnetische Energie der γ-Quanten auf die an diesen
Wechselwirkungsprozessen beteiligten Hüllenelektronen übertragen,
wodurch die Atome ionisiert werden. Die dadurch freigesetzten
energiereichen Elektronen werden ihrerseits durch elastische und
unelastische Stoßprozesse im Absorbermaterial abgebremst. Analog
zur Röntgenstrahlung weist die Gammastrahlung eine große Durchdringungsfähigkeit auf. Sie besitzt im Gegensatz zu geladenen Teilchen keine definierte Reichweite. Ihre Abschwächung erfolgt exponentiell gemäß dem Absorptionsgesetz.
Durch die Wechselwirkungsprozesse Fotoeffekt, Comptoneffekt
und Paarbildung (Abb. 2.12) werden energiereiche Photonen
(Röntgenstrahlung oder Gammastrahlung) beim Durchgang durch
Materie abgeschwächt.
a) Fotoeffekt: Absorption eines Photons und Ionisierung des Atoms
in einer inneren Schale (hier: K-Schale).
78
2.6 Wechselwirkung ionisierender Strahlung mit Materie
b) Comptoneffekt: Elastischer Stoß eines Photons mit der Frequenz
f mit einem lose gebundenen äußeren Elektron. Ein Teil der Photonenenergie wird dabei auf das Elektron übertragen. Unter Vernachlässigung der Bindungsenergie des Elektrons ergibt sich für
den Energieübertrag ∆E = h ⋅ f − h ⋅ f ′ . Die Restenergie verbleibt beim Photon, das sich unter Richtungsänderung (Streuung) mit reduzierter Frequenz f ′ < f weiterbewegt.
c) Paarbildung: Photonen mit Energie von mehr als 1,022 MeV
können im Coulombfeld eines Atomkerns materialisieren. Dabei
entsteht ein Elektron-Positron-Paar. Man nennt diesen Prozess
Paarbildung. Das Positron ist ein elektrisch positiv geladenes
Elektron mit identischer Masse me. Es stellt das Antiteilchen
zum Elektron dar. Zur Bildung des Elektron-Positron-Paares
muss das Photon mindestens eine der Ruhemasse der beiden
erzeugten Teilchen äquivalente Energie E besitzen:
E ≥ me c 2 + me c 2 = 511 keV + 511 keV = 1,022 MeV .
(2.43)
Fotoeffekt
–
e
K
L
hf
M
N
Compton-Effekt
hf’
–
e
hf
K
L
M
N
Paarbildung
e
+
–
e
hf
Atomkern
Abb.2.13: Wechselwirkungsprozesse von γ-Quanten mit Atomen
Die Gammastrahlung entsteht im Gegensatz zur Röntgenstrahlung
im Atomkern. Sie ist eine elektromagnetische Kernstrahlung. Trifft
79
2 Kernphysik
energiereiche Photonenstrahlung wie Gammastrahlung oder Röntgenstrahlung auf Materie, dann findet aufgrund der oben genannten
Wechselwirkungsprozesse eine Abschwächung der PhotonenStrahlungsintensität statt. Die Wahrscheinlichkeit, mit der einer der
genannten Wechselwirkungsprozesse auftritt, wird als Wirkungsquerschnitt σ bezeichnet. Der Wirkungsquerschnitt stellt anschaulich
ein Maß für die Trefferfläche dar, die ein Atom einem einfallenden
Photon der Gammastrahlung entgegenstellt. In Abbildung 2.13 sind
die Wirkungsquerschnitte für die Wechselwirkungen von Photonen
mit Blei als Funktion der Photonenenergie Eγ dargestellt.
Der gesamte Wechselwirkungsquerschnitt σtotal ergibt sich als Summe der Wirkungsquerschnitte für den Fotoeffekt σFoto, die ComptonStreuung σCompton und die Paarbildung σPaar:
(2.44)
σ total = σ Foto + σ Compton + σ Paar
σ
30
20
σ
σ
to t a l
p a a r
10
σ
C o m p to n
σ
F o to
0
1
2
5
10
Eγ/MeV
Abb. 2.14: Wirkungsquerschnitte für Photonenwechselwirkung mit
Pb-Atomen
Beim Durchgang durch Materie führen diese atomaren Wechselwirkungsprozesse zu einer Abschwächung der Photonen-Strahlungsintensität.
Abbildung 2.15 zeigt diese Abschwächung, die beim Auftreffen
einer Strahlungsintensität I0 auf eine Materieschicht der Dicke x auftritt.
80
2.6 Wechselwirkung ionisierender Strahlung mit Materie
I
0
I
X
Abb. 2.15: Schwächung einer Strahlungsintensität beim Durchgang
durch Materie
In einer dünnen Schicht der Dicke ∆x ist die Abnahme der Strahlungsintensität − ∆I proportional zur vorhandenen Intensität I und
zur Schichtdicke ∆x . Es gilt:
(2.45)
− ∆I = µ ⋅ I ⋅ ∆x
Dabei ist µ eine materialspezifische Konstante, die die Abschwächungseigenschaften der Materieschicht beschreibt. Fällt eine Röntgen- oder Gammastrahlung mit einer Intensität I0 auf Materie, dann
beträgt die Intensität I nach Durchlaufen einer Strecke der Dicke x
noch
I ( x) = I 0 e − µx .
(2.46)
Die stoffspezifische Konstante µ heißt linearer Schwächungskoeffizient. Er hat die Einheit cm–1. Die Halbwertsdicke d1/2 kennzeichnet die Schichtdicke einer Substanz, in der sich die Intensität der
elektromagnetischen Strahlung um 50 %, d. h. um die Hälfte des
Ausgangswertes reduziert. Es gilt:
d1 =
2
ln 2
µ
=
0,693
µ
.
(2.47)
Der lineare Schwächungskoeffizient µ hängt stark von der Frequenz
und damit von der Photonenenergie E = h ⋅ f der Röntgen- bzw.
Gammastrahlung ab.
Ionisierende Strahlung kann durch Absorption in Materie abgeschirmt werden. Die freiwerdende radioaktive Zerfallsenergie führt
dabei letztlich zu einer Erwärmung des Materials.
Beispiel:
0,1 g Radium, das sich in einem mit 10 g Wasser gefüllten,
thermisch isolierten Dewar-Gefäß befindet, bewirkt eine Erwärmung des Wassers von 1°C pro Stunde.
81
2 Kernphysik
2.7
Nachweismethoden für ionisierende Strahlung
Die aus dem Atomkern stammende ionisierende Strahlung wird mit
Kernstrahlungsdetektoren nachgewiesen und gemessen.
Die ionisierende Strahlung wird unterschieden in:
–
–
direkt ionisierende Strahlung (α-,β -Strahlung),
indirekt ionisierende Strahlung (γ -Strahlung, n-Strahlung)
Während die direkt ionisierende Strahlung aus elektrisch geladenen
Teilchen besteht, setzt sich die indirekt ionisierende Strahlung aus
elektrisch neutralen Teilchen zusammen.
Zum experimentellen Nachweis von α-,β - und γ -Strahlen wird
ihre ionisierende Wirkung in Strahlungsdetektoren (lat. detectum:
nachgewiesen) ausgenutzt. Szintillationsdetektoren beruhen auf der
Erzeugung eines Lichtsignals durch Lichtemission infolge von Stoßanregung beim Durchgang ionisierender Strahlung durch geeignete
Absorbersubstanzen (Beispiel: NaJ-Kristalle). In Ionisationsdetektoren befindet sich die Absorbersubstanz im elektrischen Feld eines
Plattenkondensators. Beim Durchgang von geladenen Teilchen durch
Materie übertragen die Teilchen durch Stoßprozesse Energie auf die
Hüllenelektronen und ionisieren dabei die Atome des durchstrahlten
Mediums. Es entstehen dabei Ionenpaare aus Elektronen und
elektrisch positiv geladenen Atomrümpfen, deren Bewegung im
elektrischen Feld ein messbares Stromsignal hervorruft. Wird das
nachzuweisende Teilchen vollständig im Zählervolumen gestoppt, so
ist die Anzahl der durch Ionisationsprozesse hervorgerufenen Elektronen der Energie des einfallenden Teilchens direkt proportional. Die
Teilchendetektoren erlauben somit prinzipiell eine Energiebestimmung der nachzuweisenden Strahlung.
Beispiel: Geiger-Müller-Zählrohr
Das Geiger-Müller-Zählrohr stellt ein einfaches Beispiel der
Realisierung eines Kernstrahlungsdetektors dar. Im Jahre 1928
hat der 1882 in Neustadt an der Weinstraße geborene Physiker
Hans Geiger zusammen mit seinem damaligen Doktoranden
Walter Müller ein so genanntes Auslösezählrohr entwickelt, das
heute Geiger-Müller-Zählrohr genannt wird.
82
2.7 Nachweismethoden für ionisierende Strahlung
Eintrittsfenster
Zählrohrdraht
Metallgehäuse
C
V
Zähler
2198
7
R (10 Ohm)
γ
Gas
U
B
Abb. 2.16: Aufbau eines Geiger-Müller-Zählrohres
Ein Geiger-Müller-Zählrohr ist ein Ionsiationszähler. Es arbeitet
nach dem Prinzip der Gasverstärkung und besteht aus einem dünnwandigen Rohr als Kathode, das mit dem negativen Pol einer Spannungsquelle verbunden ist. In der Mitte entlang der Rohrachse befindet sich ein dünner Zähldraht. Er ist mit dem positiven Pol der Spannungsquelle verbunden und bildet die Anode. Als Füllgas wird das
Edelgas Argon bei Unterdruck verwendet. Mit anderen Worten: Das
Geiger-Müller-Zählrohr besteht aus einem gasgefüllten Zylinderkondensator.
Beim Geiger-Müller-Zähler ruft jede Ionisation eine Gasentladung
hervor, die unabhängig von der Energie des nachzuweisenden Teilchens ist. Wird durch ionisierende Strahlung, z. B. durch ß-Teilchen,
eine elektrische Entladung ausgelöst, fließt ein kurzzeitiger Strom
(Stromstoß), der an einem Arbeitswiderstand R zu einem Spannungsabfall führt und somit eine Änderung ∆U der Spannung des
Zählrohrdrahtes hervorruft. Diese kurzzeitige Änderung, die man als
Spannungsimpuls bezeichnet, wird über einen Koppelkondensator C
zur weiteren elektrischen Verarbeitung an einen Verstärker mit nachfolgendem Zähler übertragen. Die in der Gasfüllung des Zählrohres
durch das einfallende ionisierende Teilchen primär gebildeten Elektronen nehmen im elektrischen Feld zwischen Zähldraht und Zählrohrwand Energie auf und tragen selbst durch Stoßionisation zur
Ladungsvervielfachung durch Elektronen-Lawinenbildung bei. Sie
verstärken dadurch das elektrische Messsignal.
83
2 Kernphysik
– Elektron
–
Gasionen
Elektronenlawine
Sekundär-Elektronen
Anodendraht
Abb. 2.17: Illustration der Ladungsvervielfachung
Die Gasverstärkung hat dabei den Faktor 108, d. h. aus einem primär
gebildeten Elektron entsteht eine Elektronenlawine von 108 Elektronen, die den Zähldraht erreichen.
Wichtig für ein GM-Zählrohr ist die Zählrohrcharakteristik n = f(U).
n ist die produzierte Ionenzahl als Funktion der angelegten Zählrohrspannung U. Normalerweise wird das GM-Zählrohr bei U ≈ 1000 V
betrieben. Man muss allerdings Vorkehrungen treffen, damit die
erzeugten Ladungslawinen nicht zu einer Dauerentladung im Zählrohr führen. Dem Zählrohrgas wird dazu ein Löschgas (z. B. Alkoholdampf) zugegeben. Der Arbeitswiderstand R begrenzt die Stromstärke und verhindert die selbständige Entladung (Dauerentladung),
die das GM-Zählrohr unbrauchbar machen würde.
Der technische Vorteil des GM-Zählers ist seine einfache Konstruktion und Robustheit. Er wird daher für militärische Strahlenschutzzwecke und im Zivilschutz eingesetzt. Ferner ist das Zählrohr unempfindlich gegenüber Spannungsschwankungen. Es besitzt jedoch
auch zwei gravierende Nachteile:
1.
Das GM-Zählrohr liefert keine Information darüber, welcher Art
(α- β - oder γ-Teilchen) die ionisierende Strahlung ist, welche die
Messimpulse auslösen. Daher ist eine Teilchenidentifizierung
unmöglich.
2.
Es kann keine Aussage über die Energie der nachzuweisenden
Teilchen gemacht werden. Daher ist eine Energiebestimmung
der Strahlung unmöglich.
Das Geiger-Müller-Zählrohr ist daher für Strahlendosismessungen
ungeeignet, denn der Zähler erzeugt unabhängig von der Teilchen-
84
2.8 Strahlenschutz
energie immer die gleichen Signale. Durch die großen Elektronenlawinen, die durch die Stoßionisationen hervorgerufen werden, benötigt das Zählrohr nach dem Durchgang eines nachzuweisenden Teilchens sehr lange (etwa 1 ms), bis er wieder einsatzbereit ist. Während dieser so genannten Totzeit kann es daher nicht messen und
eignet sich somit nicht zum Nachweis hoher Zählraten (R > 1000).
Unter der Zählrate R versteht man dabei die Anzahl dN der im Zeitraum dt nachgewiesenen Teilchen.
R=
dN
= N&
dt
(2.48)
Bei einer Zählrate von R = 100 s–1 werden 100 Teilchen in 1 s nachgewiesen. Für den Nachweis von γ-Strahlung ist die Ansprechwahrscheinlichkeit des Zählrohres kleiner als 1, d. h. nicht jedes einfallende γ-Teilchen erzeugt ein Signal. Vielmehr gehen die meisten
γ-Teilchen ungehindert durch das Zählrohr hindurch, ohne registriert
zu werden.
2.8
Strahlenschutz
Im Strahlenschutz ist die Angabe der Aktivität einer radioaktiven
Substanz nicht ausreichend. Zur quantitativen Beschreibung der
Strahlenwirkung einer ionisierenden Strahlung wurde daher die
Energiedosis D eingeführt, die im Rahmen von Strahlenschutzmessungen von grundsätzlicher Bedeutung ist. Anders als in der
Toxikologie üblich, versteht man unter dem Begriff Dosis nicht die
aufgenommene Menge einer radioaktiven Substanz. Sie ist vielmehr
ein quantitatives Maß für die Strahlenbelastung, die in Form von
äußerer Bestrahlung auch ohne Aufnahme radioaktiver Stoffe in den
Körper auftritt.
Unter der Energiedosis D versteht man den Quotienten aus der auf
das Material übertragenen Strahlenenergie dED und der Masse dm
des Absorbers. Dabei ist dED die gesamte Energie, die auf das Material in einem Volumenelement dV übertragen wird, und dm = ρ ⋅ dV
ist die Masse des Materials mit der Dichte ρ in diesem Volumenelement. Bei allen Angaben der Energiedosis muss das Bezugsmaterial
– wie z. B. Luft, Wasser oder Aluminium – angegeben werden.
D=
[ D] = 1
dE D
dm
J
= 1 Gray (Gy )
kg
(2.49)
(2.50)
Der Einheitenname der Energiedosis geht auf den englischen Naturforscher Louis Harold Gray (1905 – 1965) zurück, den Begründer
85
2 Kernphysik
der Radiobiologie. Bei der Definition der Einheit der Energiedosis
kommt es nicht auf die Energie der einfallenden ionisierenden Strahlung an, sondern nur auf den Anteil der Energie, der auf die Materie
durch Absorption übertragen wird. Denn nur dieser Anteil kann in
dem absorbierenden Medium eine chemische oder biologische Wirkung hervorrufen.
Unter der Energiedosisleistung D& versteht man den Differentialquotienten der Energiedosis nach der Zeit:
dD
.
D& =
dt
(2.51)
Für die SI-Einheit der Energiedosisleistung erhält man:
Gy
J
W
.
[ D& ] = 1
=1 =1
kg ⋅ s
kg
s
(2.52)
Dosimeter sind Strahlungsmessgeräte, die die an einem bestimmten
Ort auftreffende Strahlung über einen festgelegten Zeitraum aufsummieren.
Notwendige Voraussetzung für die Wirkung einer ionisierenden
Strahlung ist die Übertragung von Energie auf Materie. Das Ausmaß
der Wirkung hängt daneben noch von der Art der Energieübertragung ab. Sie wird durch die so genannte Ionisationsdichte bestimmt,
d. h. die Anzahl der Ionisierungsprozesse bezogen auf die im Absorber zurückgelegte Wegstrecke des ionisierenden Teilchens.
Da die verschiedenen Strahlungsarten bei gleicher Energiedosis D
unterschiedliche biologische Wirkungen verursachen, wurde der
Begriff der Äquivalentdosis H eingeführt.
H =q⋅D
(2.53)
Der Proportionalitätsfaktor q ist ein dimensionsloser Bewertungsfaktor, der die unterschiedliche Ionisationsdichte der verschiedenen
Strahlungsarten berücksichtigt und damit der unterschiedlichen Gefährlichkeit einzelner Strahlenarten Rechnung trägt. Er gibt an, um
wie viel die biologische Wirkung einer Strahlung größer ist als die
von Gamma- oder Röntgenstrahlung, für die unabhängig von der
Photonenenergie q = 1 festgesetzt wird. Für Betastrahlen ist für alle
Energien q = 1. Für Neutronenstrahlen ist der Bewertungsfaktor
energieabhängig und es gilt: q = 5 für Neutronenenergien unterhalb
10 keV. Für Neutronenenergien zwischen 10 keV und 100 keV ist
q = 10 und für Energien oberhalb 100 keV bis zu 2 MeV ist q = 20.
Für Alphastrahlen ist für alle Teilchenenergien q = 20. Diese Bewertungsfaktoren werden auch als Qualitätsfaktoren bezeichnet und
wurden durch die internationale Strahlenschutzkommission (ICRP:
International Commission on Radiation Protection) festgelegt. In der
86
2.8 Strahlenschutz
novellierten Fassung der deutschen Strahlenschutzverordnung vom
20. Juli 2001 (Fundstelle: BGBl I 2001, 1714) werden die Bewertungsfaktoren als Strahlungs-Wichtungsfaktoren w R bezeichnet
und sind dort in Anlage VI Teil C tabelliert. Für die SI-Einheit der
Äquivalentdosis gilt:
[ H ] = [q ][ D ] =
J
= 1 Sv (Sievert ) .
kg
(2.54)
Durch den Einheitennamen der Äquivalentdosis H wird der schwedische Strahlenphysiker Rolf Maximilian Sievert (1896 – 1966) für
seine Verdienste in der Strahlenschutzforschung gewürdigt. Als Einheit für die Äquivalentdosis könnte ebenfalls das Gray benutzt werden. Da es sich aber um eine mit einem dimensionslosen Bewertungsfaktor q gewichtete Energiedosis handelt, wurde um Verwechslungen auszuschließen ein eigener SI-Einheitenname eingeführt. Das
Symbol H für die Äquivalentdosis leitet sich von dem englischen
Begriff hazard (Gefahr, Wagnis) ab. Für Strahlenschutzzwecke können gleiche Äquivalentdosen H i = qi ⋅ Di verschiedener Strahlenarten i im Hinblick auf ihre biologische Wirksamkeit gleich bewertet
werden. Die Äquivalentdosis ist jedoch wegen ihrer Abhängigkeit
von dem Bewertungsfaktor q der direkten Messung nicht zugänglich.
Sie muss vielmehr aus der Energiedosis berechnet werden und setzt
die Kenntnis der Strahlenart und der Strahlenenergie voraus.
Unter der Ortsdosis versteht man die an einem bestimmten Ort gemessene Äquivalentdosis für Weichteilgewebe. Das Weichteilgewebe wird dabei als homogenes Material mit genau definierter Zusammensetzung angesehen. Die Ganzkörperdosis ist der Mittelwert der
über Kopf, Rumpf, Oberarme und Oberschenkel gemessenen Äquivalentdosis, wobei eine homogene Bestrahlung des ganzen Körpers
angenommen wird.
Ionisierende Strahlung kann genetische (gr. genos: Nachkomme) und
somatische (gr. soma: Körper) Strahlenschäden verursachen. Unter
genetischen Schäden versteht man die ausschließlich an der Nachkommenschaft beobachteten Erbschäden, die infolge einer Strahlenbelastung der Keimdrüsen der Eltern hervorgerufen wurde. Ursache
dafür sind strahleninduzierte Veränderungen an der Desoxyribonukleinsäure (DNS), wo die Erbinformation gespeichert ist. Sie führen
zu Erbgutveränderungen, die Mutationen genannt werden. Somatische Strahlenschäden betreffen dagegen nur den Körper des der
Strahlung direkt ausgesetzten Individuums.
Man unterscheidet somatische Früh- und Spätschäden. Die somatischen Frühschäden reichen von einer vorübergehenden Hautrötung
bis zur Schwächung der Schutz- und Abwehrfunktionen des Körpers
(Strahlenkrankheit). Unter den somatischen Spätschäden versteht
man die durch Bestrahlung des Körpers mit einer Zeitverzögerung
von bis zu 20 Jahren verursachten Krebserkrankungen.
87
2 Kernphysik
Die verschiedenen Körperzellen zeigen eine unterschiedliche Strahlungsempfindlichkeit, die bei gleichem Zelltyp auch noch altersabhängig ist. Kinder sind strahlungsempfindlicher als Erwachsene.
Auch die zeitliche Verteilung der Strahlendosis ist für die biologische Wirkung von Bedeutung. Eine über einen längeren Zeitraum
durch mehrere kleine Strahlendosen hervorgerufene Strahlenbelastung hat geringere biologische Strahlenwirkungen als eine einmalige
kurzzeitige Bestrahlung gleicher Gesamtdosis. Auf die Einwirkung
von Strahlung reagiert das Immunsystem des Körpers mit Abwehrmechanismen. Das Immunsystem wird unterstützt durch ein Reparatursystem, das Molekül- und Zellschäden reparieren kann. Die strahlungsinduzierte Mutation ist daher nicht gleichbedeutend mit einem
somatischen oder genetischen Schaden.
Ionisierende Strahlung
Physikalische Effekte
durch Strahlungsabsorption
Molekulare Veränderungen
Zelluläre Veränderungen
Körperzellen
Somatische
Frühschäden
Somatische
Spätschäden
Nichtstochastische Schäden
Keimzellen
Strahlenkrebs
(Leukämie und
maligne
Tumore)
Genetische
Schäden
(Nachkommen)
Stochastische Schäden
Abb. 2.18: Wirkungen ionisierender Strahlung
Als letale Dosis bezeichnet man die Äquivalentdosis einer ionisierenden Strahlung, die bei kurzzeitiger Ganzkörperbestrahlung ausreicht, um den Tod des bestrahlten Individuums herbeizuführen. Die
mittlere Letaldosis (LD50) ist dabei die Dosis, die bei der Hälfte der
Individuen, die ähnlich bestrahlt wurden zum Tode führt. Sie liegt
beim Menschen bei 4 Sv. Dies entspricht einer Energiedosis einer
γ−Strahlung von 4 Gy.
Zur einheitlichen Bewertung von gleichförmiger und ungleichförmiger Strahlenexposition des Körpers wurde für Strahlenschutzzwecke
das Konzept der effektiven Äquivalentdosis eingeführt. Wird der
88
2.8 Strahlenschutz
menschliche Körper einer ionisierenden Strahlung ausgesetzt, so
kann aus der Strahlenbelastung einzelner Körperteile und Organe die
einem Gesamtrisiko entsprechende Gesamtstrahlenbelastung errechnet werden. Dazu werden die in den einzelnen Körperregionen und
Organen vorhandenen Äquivalentdosen Hi mit dimensionslosen Gewebe-Wichtungsfaktoren w T,i multipliziert und aufsummiert.
Diese Wichtungsfaktoren w T,i berücksichtigen die unterschiedliche
biologische Strahlenempfindlichkeit des jeweiligen Organs oder
Körperteils. Der Summenwert wird als effektive Äquivalentdosis
H eff bezeichnet.
n
H eff =
∑ w T,i ⋅ H i
(2.55)
i =1
Addiert werden hierbei entgegen dem Augenschein nicht Äquivalentdosen verschiedener Organe, sondern Risikobeiträge der Organe,
die die Dimension einer Äquivalentdosis besitzen. Denn das der Bestrahlung ausgesetzte Individuum ist in seiner gesundheitlichen Integrität immer nur durch das Gesamtrisiko gefährdet. Die Einheit der
effektiven Äquivalentdosis ist, wie die für die Äquivalentdosis, das
Sievert (Sv). Die Wichtungsfaktoren sind normiert, und es gilt:
n
∑ w T ,i = 1
(2.56)
i =1
Die Wichtungsfaktoren w T,i zur Berechnung der effektiven Äquivalentdosis Heff sind in der Strahlenschutzverordnung in der novellierten Fassung von 2001 tabelliert. Die effektive Äquivalentdosis stellt
somit einen einheitlichen Vergleichsmaßstab zur Risikobeurteilung
von Strahlenbelastungen verschiedener Organe dar.
Organ bzw. Gewebe
Wichtungsfaktor w T
Keimdrüsen
0,20
Knochenmark
0,12
Lunge
0,12
Dickdarm
0,12
Brust
0,12
Schilddrüse
0,05
Knochenoberfläche
0,01
Haut
0,01
alle anderen Organe
0,25
Summe:
1,00
Tabelle 2.2: Auswahl von Gewebe-Wichtungsfaktoren w T zur Berechnung der effektiven Äquivalentdosis
89
2 Kernphysik
Beispiel:
Erhalten bei einer Ganzkörperbestrahlung von außen alle
Körperteile die gleiche Äquivalentdosis Hi = konst., so ist
die effektive Äquivalentdosis Heff identisch mit dieser Äquivalentdosis Hi:
n
H eff =
∑
i =1
n
w T,i ⋅ H i = H i ⋅
∑ w T,i = H i ⋅1 = H i
i =1
Wird jedoch durch die Aufnahme von radioaktiven Iod-131
durch die Schilddrüse ausschließlich dieses Organ mit einer
Äquivalentdosis von Hi = 2 mSv belastet, so beträgt die
effektive Äquivalentdosis
H eff = w T ,i ⋅ H i = 0,05 ⋅ 2 mSv = 0,1 mSv.
Dieses Ergebnis lässt sich wie folgt interpretieren: Das Krebsrisiko
infolge einer Bestrahlung der Schilddrüse mit Hi = 2 mSv ist dem
Krebsrisiko einer Ganzkörperbestrahlung mit einer Äquivalentdosis
von H = 0,1 mSv äquivalent.
Aufgrund des derzeitigen Kenntnisstandes werden biologische Strahlenwirkungen in nichtstochastische und stochastische Wirkungen
unterteilt. Strahlenwirkungen, deren Eintreten nicht von der Wahrscheinlichkeit abhängig ist, heißen nichtstochastisch. Die Ausprägung nichtstochastischer Wirkungen ist an einen Schwellenwert gebunden und setzt somit eine Mindestdosis voraus. Der verursachte
Strahlenschaden wird umso schwerwiegender, je höher die Dosis
war. Strahlungsinduzierte Hautverbrennungen oder die Linsentrübung im Auge stellen Beispiele für nichtstochastische Wirkungen
dar.
90
2.8 Strahlenschutz
W
100%
0
Ds
D/Gy
Ss
S
0
Ds
D/Gy
Abb. 2.19: Nichtstochastische Strahlenwirkungen
Strahlenwirkungen, bei denen kein Schwellenwert nachgewiesen
ist, heißen stochastisch. Bei stochastischen Schäden wächst mit zunehmender Dosis die Eintrittshäufigkeit und nicht das Ausmaß
des Strahlenschadens. Die Strahlenwirkung ist dann unabhängig
von der Höhe der verursachenden Dosis. Mit wachsender Dosis
steigt jedoch die Wahrscheinlichkeit für das Auftreten des Strahlenschadens an. Die wichtigste stochastische Strahlenwirkung ist die
Krebsentstehung. Strahleninduzierte Tumore stellen somatische
Schäden dar. Sie können unter Umständen erst nach einer jahrzehntelangen Latenzzeit auftreten. Aber auch genetische Schäden sind
stochastischer Natur. Die Abschätzung des Strahlenrisikos basiert
auf Untersuchungen der Krebshäufigkeit an den Überlebenden der
Atombombenabwürfe über den japanischen Städten Hiroshima und
Nagasaki vom 6. und 9. August 1945.
91
2 Kernphysik
W
W0
0
D/Gy
S
S0
0
D/Gy
Abb. 2.20: Stochastische Strahlenwirkungen
Die realistische Abschätzung des Risikos der Krebsentstehung durch
stochastische Strahlenwirkung bei niedriger Dosis stellt das Hauptproblem des Strahlenschutzes dar. Die Beurteilung der Wirkung von
geringen Strahlendosen ist schwierig, da die Quantifizierung von
Risiken erheblichen Unsicherheiten unterliegt. Die experimentell
gesicherten Erkenntnisse basieren auf Untersuchungen mit hohen
Strahlendosen, die in den Bereich niedriger Dosen extrapoliert werden müssen. Neben einer Vielzahl von chemisch kanzerogenen Substanzen, denen alle Menschen mehr oder weniger stark ausgesetzt
sind, gibt es auch ein spontanes Auftreten von Karzinomen. Die
Sterblichkeit infolge von Krebserkrankungen liegt in Deutschland
bei etwa 22%. Für eine mögliche Risikoerhöhung durch ionisierende
Niedrigstrahlung gibt es keine statistisch gesicherten Daten. Aus
Sicherheitsgründen geht man im Strahlenschutz aber davon aus, dass
eine Schwellendosis, unterhalb derer mit Sicherheit ein Strahlenschaden auszuschließen ist, nicht existiert. Aufgrund der auf der Erde
immer vorhandenen kosmischen und terrestrischen Strahlung sind
jedoch alle Menschen stets einer natürlichen Strahlenbelastung ausgesetzt.
Der Umgang mit radioaktiven Stoffen wird in Deutschland durch das
Atomgesetz und die Verordnung über den Schutz vor Schäden durch
ionisierende Strahlung, kurz Strahlenschutzverordnung (StrlSchV)
genannt, geregelt. Die Verordnung findet Anwendung für radioaktive
Stoffe mit einer Teilchen- oder Photonengrenzenergie von mindestens 5 keV. Für Elektronenstrahlung ist die Strahlenschutzverordnung anzuwenden, wenn die Elektronenenergie 3 MeV überschreitet.
Unter Umgang versteht man dabei die Verwendung, Beförderung
92
2.8 Strahlenschutz
und Lagerung von radioaktiven Stoffen. Je nach Aktivität der radioaktiven Stoffe ist der Umgang genehmigungsfrei oder genehmigungsbedürftig. Für den genehmigungsfreien Umgang mit radioaktiven Stoffen sind in Anlage IV der StrlSchV Freigrenzen einzelner
Radionuklide aufgeführt. Diese Freigrenze liegt beispielsweise für
Cs-137 bei einer Aktivität von A = 1 ⋅10 4 Bq . Für den Umgang mit
radioaktiven Stoffen legt die Strahlenschutzverordnung Grenzwerte
für die Strahlenexposition fest, die nicht überschritten werden dürfen.
Der Grenzwert für die jährliche effektive Äquivalentdosis beträgt
zurzeit (Stand: 2004) für beruflich strahlenexponierte Personen 20
mSv/a. In der Vorläuferversion der StrlSchV in der Fassung von
1989 war dieser Grenzwert bei 50 mSv/a festgelegt. Im Rahmen der
Neuregelung der StrlSchV erfolgte auch eine Absenkung der Dosisgrenzwerte für die Bevölkerung. Zum Schutz der Bevölkerung vor
Strahlenexpositionen aus zielgerichteter Nutzung radioaktiver Stoffe
und ionisierender Strahlung wurde der Grenzwert von bisher 1,5
mSv auf 1 mSv im Kalenderjahr abgesenkt. Ausgedehnt wurde der
Strahlenschutz auch auf Strahlenexpositionen durch natürliche
Strahlungsquellen. Für Expositionen aus natürlichen Strahlungsquellen wurde ein Grenzwert für die effektive Dosis von 20 mSv im
Kalenderjahr vorgeschrieben. Einbezogen wurde dabei auch ausdrücklich das Flugpersonal hinsichtlich der Belastung durch kosmische Strahlung. Die Flugzeugbetreiber wurden zur Ermittlung der
Strahlenexposition ihres fliegenden Personals verpflichtet, sobald die
effektive Dosis im Kalenderjahr 1 mSv überschreiten kann. Der
Grenzwert für fliegendes Personal für die effektive Dosis durch
kosmische Strahlung beträgt 20 mSv pro Kalenderjahr.
Zum Vergleich: Die mittlere natürliche Strahlenexposition aus allen
natürlichen Strahlenquellen führt in Deutschland zu einer jährlichen
effektiven Äquivalentdosis von 2,4 mSv/a mit einer lokalen Schwankungsbreite zwischen 1,5 und 4 mSv/a. Zur natürlichen Strahlenexposition trägt die externe Strahlenexposition zu einem Viertel bei.
Sie wird verursacht durch die kosmische Strahlung (Höhenstrahlung)
und die terrestrische Strahlung infolge der natürlichen Radionuklide
von Kalium-40 und den Nukliden der Uran- und Thorium-Reihe, die
sich im Erdboden befinden. Zu drei Viertel trägt die interne Strahlenexposition zur natürlichen Strahlenbelastung bei. Sie wird durch
inkorporierte Radionuklide hervorgerufen, die mit der Nahrung aufgenommen oder - die wie das radioaktive Edelgasnuklid Radon-222 mit der Luft inhaliert werden. Der Mittelwert der Radonkonzentration in Häusern und Wohnungen liegt bei etwa 50 Bq pro Kubikmeter
Luft. Im Freien beträgt in Deutschland die Radonkonzentration etwa
15 Bq/m³.
Gleichzeitig gilt für die effektive Berufslebensdosis von beruflich
strahlenexponierten Personen ein Grenzwert von 400 mSv. Die
Summe sämtlicher jährlichen effektiven Äquivalentdosen darf während eines Berufslebens maximal 400 mSv betragen. Dabei gilt jedoch das Prinzip der Dosisminimierung unterhalb der Grenzwerte.
93
2 Kernphysik
Dieses Minimierungsgebot wird „ALARA“-Prinzip (as low as
reasonably achievable) genannt und fließt in Form der Strahlenschutzgrundsätze in § 28 Abs. 1 der Verordnung ein. Demnach ist
beim Umgang mit radioaktiven Stoffen jede unnötige Strahlenexposition von Personen zu vermeiden.
Der Zerfall natürlicher Radionuklide verursacht in der Strahlungsmesstechnik auch bei Abwesenheit von künstlichen Strahlungsquellen eine immer vorhandene Untergrundrate von ionisierenden Ereignissen, die als Nulleffekt bezeichnet wird.
Literaturhinweis: Martin Volkmer, Radioaktivität und Strahlenschutz, Informationskreis KernEnergie, Berlin
2.9
Übungsaufgaben zu Kapitel 2
Aufgabe 1
C-14 ( T1/ 2 = 5730 a ) und K-40 ( T1/ 2 = 1,28 ⋅ 10 9 a) sind zwei natürliche und Sr-90 (T1/ 2 = 28,64 a) sowie Cs-137 (T1/ 2 = 30,17 a) sind
zwei künstliche Betastrahler. Geben Sie für diese radioaktiven Stoffe
jeweils die Zerfallsgleichung nach dem 2. Verschiebungssatz von
Rutherford und Soddy an!
Aufgabe 2
Gegeben seien 108 Radiumatome. Sie wandeln sich durch radioaktiven α−Zerfall mit einer Halbwertszeit von T1/2 = 1600 a in Radonatome um. Wie viele Zerfallsprozesse finden dabei innerhalb eines
Tages statt?
Aufgabe 3
In welches Nuklid wandelt sich
238
U
92
nach einem α−Zerfall und
zwei weiteren β−Zerfällen um? Geben Sie eine formelmäßige Beschreibung der Zerfallskette an.
Aufgabe 4
Ein γ−Strahl mit einer Energie von 1 MeV trifft mit einer Intensität
I0auf eine zur Abschirmung eingesetzte Stahlplatte mit 30 mm Stärke
( µ = 0,47 cm −1 ).
a) Wie groß ist das Intensitätsverhältnis I / I0 hinter der
Abschirmung?
94
2.10 Musterlösungen zu Kapitel 2
b) Wie viel Prozent der auftreffenden Intensität werden
abgeschirmt?
Aufgabe 5
In einem unfallsicheren Transportbehälter für radioaktive Präparate
befinden sich 0,6 mol des Plutoniumisotops
239
Pu
94
. Seine Halb-
wertszeit beträgt T1 / 2 = 2,44 ⋅ 10 4 a . Wie groß ist
a) die Masse des radioaktiven Stoffes,
b) die Aktivität des radioaktiven Stoffes ?
2.10
Musterlösungen zu Kapitel 2
Aufgabe 1
14
14
6 C → 7 N + e + νe
40
40
19 K → 20 Ca + e + ν e
90
90
38 Sr → 39 Y + e + ν e
137
137
55 Cs → 56 Ba + e + ν e
Aufgabe 2
Für die Anzahl der zerfallenen Radiumatome ∆N gilt:
∆N = N 0 − N (t )
N 0 = 10 8 ist die Anzahl der zum Anfangszeitpunkt vorhandenen
radioaktiven Atome. Nach der Zerfallszeit t = 1 d sind noch N(t)
Radiumatome vorhanden.
∆N = N 0 − N 0 e −λt
λ ist die Zerfallskonstante.
λ=
ln 2
T1 / 2
−
∆N = N 0 (1 − e
ln 2
t
T1 / 2
) = 119
Innerhalb eines Tages finden 119 Zerfallsprozesse statt.
95
2 Kernphysik
Für kleine Exponenten x kann die Exponentialfunktion approximiert
werden. Es gilt folgende Näherungsformel:
e−x ≈ 1 − x
x=
ln 2
t
T1 / 2
∆N = N 0 (1 − e − x ) ≈ N 0 (1 − (1 − x)) = N 0 x
Folglich gilt:
∆N ≈ N 0
ln 2
t
T1 / 2
∆N ≈ 119
Aufgabe 3
238
U
92
α
→
234
Th
90
β
→
234
Pa
91
β
→
234
U
92
Aufgabe 4
Das Schwächungsgesetz lautet: I = I 0 ⋅ e − µx
a)
Für das Intensitätsverhältnis I / I 0 hinter der Abschirmung gilt:
I / I 0 = e − µx
Mit µ = 0,47 cm −1 und x = 30 mm = 3,0 cm folgt:
I / I 0 = e−1, 41 = 0,244
b) 24,4 % der auftreffenden Intensität treten durch die Abschirmung hindurch, folglich werden 75,6 % abgeschirmt.
Aufgabe 5
a) 1 Mol Pu-239 besitzt eine in Gramm gemessene Masse, die der
relativen Atommasse Ar entspricht.
Es ist: Ar(Pu-239) = 239.
96
2.10 Musterlösungen zu Kapitel 2
Mit n = 0,6 mol folgt:
m = 239 g/mol ⋅ 0,6 mol = 143,4 g .
b) Für die Aktivität A gilt:
A=λ⋅N
λ ist die Zerfallskonstante.
λ=
ln 2
= 9 ⋅ 10 −13 1 / s
T1 / 2
1 Mol enthält N A = 6,02 ⋅1023 Pu-Atome. N A ist die AvogadroKonstante. Für n = 0,6 mol folgt:
N = n ⋅ N A = 0,6 mol ⋅ 6,02 ⋅ 10 23 mol −1 = 3,6 ⋅ 10 23 Pu-Atome.
Für die Aktivität ergibt sich:
A = λ ⋅ N = 9 ⋅ 10 −13 s −1 ⋅ 3,6 ⋅ 10 23 = 3,24 ⋅ 1011 Bq = 324 GBq
97
Anhang 1: Physikalische Konstanten
Anhang 1: Physikalische Konstanten
98
Lichtgeschwindigkeit
c = 299792458m/s
Planck-Konstante
h = 6,6260755 ⋅ 10 −34 J s
Drehimpulsquantum
h = 1,05457266 ⋅10 −34 J s
Elementarladung
e = 1,60217733 ⋅ 10 −19 A s
Elektronen-Ruhemasse
m e = 9,1093897 ⋅ 10 −31 kg
Protonen-Ruhemasse
m p = 1,6726231 ⋅ 10 −27 kg
Neutronen-Ruhemasse
m n = 1,6749286 ⋅ 10 −27 kg
Elektrische Feldkonstante
ε 0 = 8,8541878 ⋅ 10 −12
Rydberg-Energie
R H = 13,605698 eV
Gravitationskonstante
G = 6,674 ⋅ 10 −11 m 3 kg −1 s −2
Avogadro-Konstante
N A = 6,0221367 ⋅ 10 23 mol −1
Boltzmann-Konstante
k = 1,380658 ⋅ 10 −23 J K −1
As
Vm
Anhang 2: Formelzeichen
Anhang 2: Formelzeichen
Symbol
Benennung
Einheit
a
spezifische Aktivität
Bq/kg
A
Aktivität
Bq
A
Auflösungsvermögen
1
A
Nukleonenzahl
1
c
Lichtgeschwindigkeit
m/s
d1/2
Halbwertsdicke
cm
D
Energiedosis
Gy
D&
Energiedosisleistung
Gy/s
E
Energie
J oder eV
EB
Bindungsenergie
J oder eV
EC
Coulomb-Energie
J oder eV
Ekin
kinetische Energie
J oder eV
Eγ
γ−Strahlungsenergie
J oder eV
EF
Oberflächenenergie
J oder eV
f
Frequenz
Hz
fG
Grenzfrequenz
Hz
H
Planck-Konstante
Js
H
Äquivalentdosis
Sv
Heff
effektive Äquivalentdosis
Sv
I
Intensität
W/m2
I
elektrische Stromstärke
A
k
Vermehrungsfaktor
1
l
Drehimpulsquantenzahl
1
L
Drehimpuls
Js
m
Masse
kg
me
Elektronenmasse
kg
mn
Neutronenmasse
kg
m0
Ruhemasse
kg
mp
Protonenmasse
kg
mu
Atommassenkonstante
kg
ml
magnetische Quantenzahl
1
99
Anhang 2: Formelzeichen
Symbol
100
Benennung
Einheit
ms
magnetische Spinquantenzahl
1
M
molare Masse
kg/mol
n
Stoffmenge
mol
ms
magnetische Spinquantenzahl
1
n
Hauptquantenzahl
1
N
Neutronenzahl
1
N
Teilchenzahl
1
N&
Zählrate
1/s
OF
Kernoberfläche
m2
p
Impuls
kg m/s
q
Qualitätsfaktor
1
r
Abstand
m
R, r
Radius
m
R
Zählrate
1/s
RA
Atomradius
m
RH
Rydberg-Konstante
eV
RK
Kernradius
m
s
Spinquantenzahl
1
T
Periodendauer
s
T1/2
Halbwertszeit
s
U
elektrische Spannung
V
V
Volumen
m3
VA
Atomvolumen
m3
Vm
molares Volumen
m3/mol
wi
Wichtungsfaktor
1
W
Arbeit
J oder eV
WA
Austrittsarbeit
J oder eV
Z
Kernladungszahl
1
∆E
Energieunschärfe
J oder eV
∆p
Impulsunschärfe
kg m/s
∆x
Ortsunschärfe
m
∆m
Massendefekt
kg
ε
Energie
eV oder J
λ
Wellenlänge
λ
Zerfallskonstante
m
1/s
Anhang 2: Formelzeichen
Symbol
Benennung
Einheit
λ min
Grenzwellenlänge
M
ρ
Dichte
kg/m3
ρK
Dichte der Kernmaterie
kg/m3
σf
Spaltwahrscheinlichkeit
b
σFoto
Wirkungsquerschnitt
b
σCompton
Wirkungsquerschnitt
b
σPaar
Wirkungsquerschnitt
b
101
Anhang 3: Periodensystem der Elemente (IUPAC)
Anhang 3: Periodensystem der Elemente (IUPAC)
102