Projekt Heinrich Ying Elektrostatik Kondensatoren

Elektrostatik
Analytische und numerische Feldberechnungen an einem
Plattenkondensator
Sebastian Heinrich, 313473
Hantao Ying, 345391
Technische Universität Berlin
Fakultät 5, Institut für Mechanik
Fachgebiet Kontinuumsmechanik und Materialtheorie
Projekt Simulationstools und ihre Anwendung
31. März 2014
2
Inhaltsverzeichnis
1
2
3
4
5
Einleitung
4
Theorie
5
2.1
Elektrodynamik . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5
2.2
Elektrostatik
6
2.3
Konstitutive Beziehungen/Polarisation . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
6
2.4
Feldgleichungen der Elektrostatik . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
8
2.5
Kapazität
8
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Analytische Feldberechnung
10
Numerische Simulation
13
4.1
Randbedingungen
4.2
Schwache Formulierung
4.3
Netzgenerierung mit Gmsh
Ergebnisse
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
13
13
14
16
3
Abbildungsverzeichnis
1
Homogenes elektrisches Feld in einem Plattenkondensator
2
Feldlinien eines geladenen Plattenkondensators [Lindner, 1992]
. . . . . . . . . . . . . . . . . .
3
Schema für Feldgleichungen sowie Rand- und Anfangsbedingungen
4
Modell eines unpolaren Atoms nach [Henke, 2007]
5
Modell eines polaren Atoms im elektrischen Feld nach [Henke, 2007]
6
Zwei Elektroden als Kondensator [Henke, 2007] . . . . . . . . . . . . . . . . . . . . . . . .
7
Parallelgeschichteter Plattenkondensator nach [Wolff, 1997]
8
Elektrisches Feld des Beispielplattenkondensators mit Aluminiumoxid
9
Elektrisches Feld des Beispielplattenkondensators mit Teflon . . . . . . . . . . . . . . . . .
12
10
Netzgenerierung mit Gmsh
15
11
Feldberechnung eines Plattenkondensators mit Dielektrikum . . . . . . . . . . . . . . . . .
16
12
Verlauf des E-Felds in einem Plattenkondensator mit Dielektrikum . . . . . . . . . . . . .
16
13
Kugeldielektrikum im ebenen E-Feld nach [Wolff, 1997]
. . . . . . . . . . . . . . . . . . .
17
14
Numerische Berechung eines Plattenkondensators mit kugelförmigem Dielektrikum . . . .
18
. . . . . . . . . . . . . . .
. . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . .
. . . . . . . . . . . . . . . . .
. . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4
4
5
7
7
9
10
12
Tabellenverzeichnis
1
Parameter für die analytische Berechnung eines Plattenkondensators mit Dielektrikum . .
11
2
Ergebnisse der analytische Berechnung eines Plattenkondensators mit Dielektrikum . . . .
11
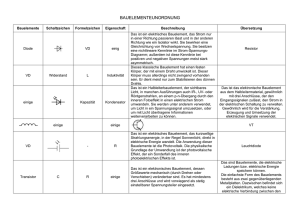
4
1
Einleitung
Ein Ziel des Projekts ist die Untersuchung von Randeffekten beim elektrischen Plattenkondensator. Abb. 1
zeigt eine idealisierte, stark vereinfachte Darstellung des elektrischen Feldes eines Plattenkondensators.
Darunter ist das tatsächliche Feld mit Randeffekten in Abb. 2 dargestellt, so wie es im Rahmen des Pro-
Abbildung 1. Homogenes elektrisches Feld in einem Plattenkondensator
jekts berechnet werden soll. Außerdem soll der Einfluss von Dielektrika auf das elektrische Feld untersucht
werden. Für die Feldberechnung steht das numerische Simulationstool FEniCS zur Verfügung.
Der Ablauf des Projekts ist wie folgt: Zuerst werden die Grundlagen der Maxwellschen Theorie erarbeitet, wobei die Elektrostatik im Vordergrund steht. Anschließend ist eine analytische Betrachtung des
Plattenkondensators mit einem dielektrischen Werkstoff zwischen den Platten durchzuführen, welche als
Vergleich für die numerische Feldberechnung dienen soll. Bei der Umsetzung mit FEniCS geht es insbesondere um die Wahl geeigneter Randbedingungen sowie eines geeigneten Rechengebietes, sodass die
homogenen Feldlinien aus der analytischen Berechnung im Volumen zwischen den Kondensatorplatten
gut nachgebildet und die Randeffekte dargestellt werden.
Abbildung 2. Feldlinien eines geladenen Plattenkondensators [Lindner, 1992]
5
2
2.1
Theorie
Elektrodynamik
Die Lösung und Interpretation der Maxwellschen Gleichungen ist das zentrale Anliegen der Elektrodynamik. Sie sind empirisch gefundene Grundgesetze der Physik und beschreiben das raumzeitliche Verhalten der primären Feldgrößen der Elektrodynamik, die elektrische Feldstärke
Induktion
𝐵.
𝐸
und die magnetische
In Differentialform lauten die Maxwellschen Gleichungen lokal in regulären Punkten:
𝜕𝐵
+ ∇ × 𝐸 = 0,
𝜕𝑡
∇ · 𝐵 = 0,
Faraday-Gesetz:
−
elektrische Ladungserhaltung:
Neben den größen
𝐸
und
𝐵,
𝜕D
+ ∇ × H = 𝑗 F + 𝑞F 𝑣,
𝜕𝑡
∇ · D = 𝑞F .
welche über die Kraftwirkung auf geladene Teilchen in elektrischen Fel-
dern einerseits und magnetischen Feldern andererseits definiert sind, findet man das Ladungspotential
in Materie
D,
sowie das Strompotential in Materie
H
in den Gleichungen. Beide Potentiale wurden aus
mathematischen Gründen bei der Beschreibung der elektrischen Ladungserhaltung eingeführt. In der
gewählten Darstellungsform ist außerdem die Stromdichte der freien Ladungen
dungsdichte
𝑞F
enthalten. Sie sind Teil der Gesamtstromdichte
𝑗
𝑗F,
sowie die freie La-
und der totalen Volumenladungsdichte
𝑞.
Zusammen mit Materialgesetzten bilden die Maxwellschen Gleichungen Feldgleichungen. Sind außerdem Rand- und Anfangsbedingungen für das elektrodynamische Problem gegeben, so ist dieses vollständig
beschrieben. Abb. 3 zeigt den Zusammenhang zwischen den einzelnen Komponenten, die für die Lösung
eines solchen Problems benötigt werden.
t
Γ
Materialgesetze
Γ
+
MaxwellGleichungen
RB
RB
=
Feldgleichungen
AB
Ω:x∊ℝ,t∊ℝ
x
Abbildung 3. Schema für Feldgleichungen sowie Rand- und Anfangsbedingungen
6
2.2
Elektrostatik
Für den Fall, dass alle Zeitableitungen verschwinden und auch keine Geschwindigkeiten vorhanden sind,
d. h.
𝜕(·)
=0
𝜕𝑡
𝑣 = 0,
und
vereinfacht sich das elektrodynamische Problem in ein elektrostatisches. Die Maxwellschen Gleichungen
vereinfachen sich ebenfalls, da alle Terme mit Zeitableitungen und Geschwindigkeiten verschwinden:
−
𝜕D
+ ∇ × H = 𝑗 F + 𝑞F 𝑣
𝜕𝑡
𝜕𝐵
+∇×𝐸 =0
𝜕𝑡
∇ · D = 𝑞F ,
⇒
∇ × H = 𝑗F,
⇒
∇ × 𝐸 = 0,
∇ · 𝐵 = 0.
Wie man sieht, entkoppeln sich unter den hier getroffenen Annahmen das magnetische und elektrische
Feld, sodass in der Elektrostatik nur zwei der vier Maxwellschen Gleichungen betrachtet werden müssen.
Die Grundeigenschaften des elektrostatischen Feldes werden durch folgende Gleichungen beschrieben:
∇ × 𝐸 = 0,
∇ · D = 𝑞F ,
D = 𝜀0 𝐸 + 𝑃 .
Neben den beiden Maxwellschen Gleichungen wird, wie bereits beschrieben, ein Materialgesetz benötigt.
𝐷 = 𝜀0 𝐸
wird dabei als Maxwell-Lorentz-Ätherrelation bezeichnet und definiert den Zusammenhang
zwischen dem elektrischen Potential
𝐷
und dem elektrischen Feld
𝐸
im Vakuum.
Aufgrund seiner Rotationsfreiheit im elektrostatischen Fall ist das elektrische Feld vollständig durch ein
skalares Potential
𝜙
charakterisiert, d. h.
𝐸 = −∇𝜙.
Dies lässt sich mit Hilfe des Satzes von Schwarz beweisen:
𝜕 𝜕𝜙
𝜕 𝜕𝜙
∇ × ∇𝜙 = 𝑒𝑖 × 𝑒𝑗
= 𝑒𝑘 𝜀𝑘𝑖𝑗
𝜕𝑥𝑖 𝜕𝑥𝑗
𝜕𝑥𝑖 𝜕𝑥𝑗
)︂
(︂
)︂
(︂
)︂
(︂
𝜕 𝜕𝜙
𝜕 𝜕𝜙
𝜕 𝜕𝜙
𝜕 𝜕𝜙
𝜕 𝜕𝜙
𝜕 𝜕𝜙
−
𝑒1 +
−
𝑒2 +
−
𝑒3 = 0.
=
𝜕𝑥2 𝜕𝑥3
𝜕𝑥3 𝜕𝑥2
𝜕𝑥3 𝜕𝑥1
𝜕𝑥1 𝜕𝑥3
𝜕𝑥1 𝜕𝑥2
𝜕𝑥2 𝜕𝑥1
2.3
Konstitutive Beziehungen/Polarisation
Unpolare und polare Dielektrika bilden unter Einfluss eines äußeren elektrischen Feldes ein mittleres
Dipolmoment
⟨𝑝𝑒 ⟩.
Die Polarisation
𝑃 = 𝑛⟨𝑝𝑒 ⟩
gibt die Dipolmomentendichte an. Abb. 4 zeigt die elektrische Polarisation anhand eines einfachen Modells
für ein unpolares Atom. Der positiv geladene Kern wird als punktförmig angesehen. Seine Ladung ist gleich
dem Produkt aus der Ordnungszahl des Atoms
𝑍
und der Elementarladung
𝑒.
Die negativen Elektronen
kreisen auf Elektronenschalen um den Kern und bilden eine homogene Elektronenwolke, welche in Form
eines Kreises um den Atomkern dargestellt ist. Ohne äußere Einflüsse heben sich die positiven und
7
Ze
Ze
+
𝛅
E
Abbildung 4. Modell eines unpolaren Atoms nach [Henke, 2007]
Ke
E
Q
𝛝
d
-Q
Ke
Abbildung 5. Modell eines polaren Atoms im elektrischen Feld nach [Henke, 2007]
negativen Ladungen im Mittel auf. Wirkt nun ein äußeres elektrisches Feld auf das Atom, so wird die
Elektronenwolke relativ zum Atomkern verschoben und es bildet sich ein Dipol.
Eine weitere Art der Polarisation ist die ionische Polarisation, wobei sich Ionen an einem elektrischen
Feld ausrichten. Die Moleküle von polaren Dielektrika sind natürliche Dipole und haben auch ohne ein
äußers elektrisches Feld ein Dipolmoment. Aufgrund thermischer Bewegungen sind diese aber zufällig
verteilt und heben sich im Mittel auf. In einem elektrischen Feld versucht ein Drehmoment die Ionen
gegen die thermischen Bewegungen entlang des Feldes auszurichten. In Abb. 5 ist ein solcher Dipol in
einem elektrischen Feld dargestellt. In einer Grupppe von Ionen zeigen die Dipolmomente nun nicht mehr
zufällig in verschiedene Richtungen, sondern bilden ein mittleres Dipolmoment.
In einem polarisierten Körper sind also die Dipole entlang des elektrischen Feldes ausgerichtet und die
positiven und negativen Ladungen heben sich aufgrund ihrer regelmäßigen Abfolge auf. Die äußersten
Dipole haben hingegen keine Nachbardipole außerhalb des Körpers, sodass sich an den Rändern positive
bzw. negative Oberflächenladungen bilden. Diese Ladungen erzeugen ein elektrisches Feld, welches dem
äußeren elektrischen Feld entgegen wirkt.
Für Stoffe mit einem linearen Zusammenhang zwischen
𝑃
und
𝑃 = 𝜀0 (𝜀r − 1)𝐸,
𝐸
gilt
8
mit der relativen Dielektrizitätskonstanten
𝜀r .
Damit ist
D = 𝜀0 𝐸 + 𝑃 = 𝜀0 𝐸 + 𝜀0 (𝜀r − 1)𝐸 = 𝜀0 𝜀r 𝐸 = 𝜀𝐸 .
2.4
Feldgleichungen der Elektrostatik
In den vorherigen Abschnitten wurden die Maxwellschen Gleichungen für statische sowie dynamische
Probleme beschrieben und das Verhalten einfacher Materie im elektrischen Feld aufgezeigt. Letzteres
führte zu den konstitutiven Beziehungen. Für eine lineare Beziehung zwischen
𝐸
und
𝑃
sollen im Fol-
genden die elektrostatischen Feldgleichungen hergeleitet werden.
Ausgehend von
∇ · D = 𝑞F
ergibt sich durch Einsetzen der konstitutiven Beziehung
D = 𝜀0 𝐸 + 𝑃 = 𝜀𝐸
aus dem vorherigen Abschnitt folgender Ausdruck:
∇ · 𝜀𝐸 = 𝑞F .
Drückt man die elektrische Feldstärke durch das skalare Potential
𝜙
aus, so erhält man die Poisson-
Gleichung des elektrostatischen Feldes:
∇ · 𝜀∇𝜙 = −𝑞F .
Für
𝜀 = homogen
und
𝑞F = 0
vereinfacht sich die Gleichung zur Laplace-Gleichung:
∆𝜙 = 0.
Diese beiden Feldgleichungen sind nicht mehr allgemeingültig, sondern beschreiben das räumliche Verhalten der elektrostatischen Größen für ein spezielles materielles Volumen.
2.5
Kapazität
Abb. 6 zeigt einen Kondensator bestehend aus zwei voneinander isolierten Elektroden. Auf der Elektrode
𝑄
1 befindet sich die positive Ladung
und auf der Elektrode 2 die negative Ladung
−𝑄.
Aufgrund
des Ladungsunterschiedes bildet sich zwischen ihnen ein elektrisches Feld aus, dessen Feldlinien in der
Abbildung zu sehen sind. Die Spannung zwischen zwei Punkten auf den beiden Elektroden ist gleich dem
Wegintegral des elektrischen Feldes zwischen den Punkten. Durch Einsetzten des elektrischen Potentials
erhält man die Spannung als Potentialunterschied:
∫︁2
∫︁2
𝐸 · d𝑠 = −
𝑈=
1
∇𝜙 · d𝑠 = 𝜙1 − 𝜙2 .
1
Sie beschreibt die Arbeit die verrichtet werden muss, um eine Ladung von Punkt 1 zu Punkt 2 zu transportieren.
Die Ladung auf Elektrode 1 lässt sich als Integral der Oberflächenladungen
𝑞S
über die Oberfläche des
Leiters beschreiben. Dies ist gleich dem Sprung der elektrischen Ladungsdichte in Normalenrichtung der
9
+
+
+
+
+
+
Elektrode 1
+
Q
-
Elektrode 2 -
+
+
-
-
-Q
-
Abbildung 6. Zwei Elektroden als Kondensator [Henke, 2007]
Oberfläche. Ersetzt man die elektrische Ladungsdichte durch das elektrische Feld und die Dielektrizitätskonstante, so kann die Ladung
𝑄
als Gradient des elektrischen Potentials in Normalenrichtung zur
Oberfläche ausgedrückt werden. Dabei wird angenommen, dass das elektrische Feld im Leiter verschwindet (𝐸 1
= 0)
und der Zusammenhang zwischen
𝑞S d𝐴 =
𝑄=
𝑃
und
∫︁
∫︁
𝜕Γ1
𝜕Γ1
JDK · 𝑛 d𝐴 =
∫︁
linear ist, d. h.
𝜀0 (𝜀𝑟2 𝐸 2 − 𝜀𝑟1 𝐸 1 ) · 𝑛 d𝐴
𝜕Γ1
∫︁
𝜀0 𝜀𝑟 𝐸 · 𝑛 d𝐴 = −𝜀0 𝜀𝑟
=
𝐸
∫︁
𝜕Γ1
∇𝜙 · 𝑛 d𝐴.
𝜕Γ1
𝜙 der linearen Laplace Gleichung genügt, kann
𝜆𝜙, und die Ladung auf der Elektrode skaliert entsprechend, 𝜆𝑄.“ Daher sei die Ladung
Nach dem Buch von Henke (2011), auf S. 77, gilt: „Da
man es skalieren,
proportional zum Gradienten des elektrischen Potentials und somit auch zur Potentialdifferenz:
𝑄 = 𝐶𝑈.
Der Proportionalitätsfaktor
𝐶
ist die Kapazität. Er ist das Verhältnis zwischen der, auf zwei voneinan-
der isolierten elektrischen Leitern befindlichen Ladungsmenge und der daraus resultierenden Spannung
zwischen den Leitern.
10
3
Analytische Feldberechnung
Für einfache Plattenkondensator-Konfigurationenen kann die Feldberechnung analytisch erfolgen. Abb. 7
𝑑𝑖 mit 𝑖 =
1,2,3. Auf den Kondensatorplatten befinde sich die Ladung 𝑄 bzw. −𝑄, 𝜎 ist die Flächenladungsdichte auf
den Platten. Die Dielektrika haben eine Elektrizitätskonstante von 𝜀𝑖 und 𝑈𝑖 ist der Spannungsabfall über
den einzelnen Schichten. Die Vektoren 𝑛 bis 𝑛3 zeigen in Normalenrichtung der Dielektrika. Schließlich ist
𝐴 eine geschlossene Fläche um die rechte Elektrode und 𝐴0 deren Abschnitt entlang der Innenseite der
zeigt einen solchen Plattenkondensator mit drei zu den Platten parallelen Dielektrika der Breite
Kondensatorplatte. Dabei werden folgende Annahmen getroffen, um die Berechnungen zu vereinfachen:
A
U1
U2
U3
𝛆1
𝛆2
𝛆3
A0
+
n
𝛔
n1 n2
d1
-𝛔
n2 n3
d3
d2
x
Abbildung 7. Parallelgeschichteter Plattenkondensator nach [Wolff, 1997]
ˆ
Der Feldbereich ist auf das Volumen zwischen den Elektroden begrenzt.
ˆ
Die Anordnung der Elektroden ist planparallel.
ˆ
Außerhalb des Kondensatorvolumens wird das Feld nicht berücksichtigt.
ˆ
Ein Streufeld am Rand des Plattenquerschnitts wird nicht modelliert, d. h. die Normalenrichtung
des elektrischen Feldes verschwindet.
Aus den Annahmen folgt für die Auswertung des Flussintegrals über die geschlossene Fläche
nur eine Feldkomponente senkrecht zur Elektrodenoberfläche
D = D𝑒𝑥
𝐴,
dass
existiert und die auf der Elek-
trode enthaltene Ladung Q gleich dem Produkt aus elektrischem Ladungspotential und der Fläche der
Elektrodeninnenseite
𝐴0
ist:
∮︁
∮︁
D · 𝑛 d𝐴 =
𝜕𝑉
D d𝐴 = D𝐴0 = 𝑄.
𝜕𝑉
Die Ladung pro Flächeneinheit auf der Innenseite der Elektrode ist
𝜎=D=
𝑄
.
𝐴0
Aus der Forderung nach der Stetigkeit des Ladungspotentials an parallelen Grenzschichten elektrisch
verschiedener Medien folgt
D(1) · 𝑛(1) = D(2) · 𝑛(2) = · · · = D(𝑛) · 𝑛(𝑛)
|D(1) | = |D(2) | = · · · = |D(𝑛) |.
11
Somit lassen sich die Feldgrößen für die einzelnen Dielektrikum-Schichten bestimmen, innerhalb einer
jeden Schicht sind die Feldgrößen konstant. Das Ladungspotential in der
D(𝑖) = D𝑒𝑥 =
i -ten Schicht ist
𝑄
𝑒𝑥 = 𝜎𝑒𝑥 .
𝐴0
Es ist nicht nur innerhalb einer Schicht konstant, sondern im gesamten Volumen zwischen den Kondensatorplatten. Die elektrische Feldstärke in der
𝐸 (𝑖) =
i -ten Schicht ist
𝑄
𝜎
D(𝑖)
=
𝑒𝑥 = (𝑖) 𝑒𝑥 = 𝐸 (𝑖) 𝑒𝑥 .
𝜀(𝑖)
𝐴0 𝜀(𝑖)
𝜀
Die Kapazität des Plattenkondensators ist gleich der Summe aus den Einzelkapazitäten der Dielektrika
und lässt sich aufgrund der getroffenen Annahmen sehr einfach berechnen:
∫︁𝑛
𝐸 · d𝑠 =
𝑈=
𝑛
∑︁
𝐸 (𝑖) 𝑑(𝑖) =
𝑖=1
1
𝑛
𝑄 ∑︁ 𝑑(𝑖)
𝐴0 𝑖=1 𝜀(𝑖)
⇒
𝐶=
𝐴0
𝑄
= ∑︀
.
𝑛
𝑈
𝑑(𝑖)
𝑖=1
𝜀(𝑖)
Im Folgenden ist ein Zahlenbeispiel für die obige Berechnung aufgeführt. Dabei wird das elektrische Feld
des Plattenkondensators aus Abb. 7 für die Dielektrika Aluminium und Teflon berechnet. Die genauen
Parameter stehen in Tabelle 1. Tabelle 2 zeigt die Ergebnisse der Rechnung. Wie man sieht, wird das
Parameter
Werte
Parameter
Werte
𝐴0
𝜀0
𝜀rELK
𝑈
0,01 m2
8,85 · 10−12 As/(Vm)
8
5V
𝑑1..3
𝜀rLuft
𝜀rTeflon
0,01 m
1,00059
2
Tabelle 1. Parameter für die analytische Berechnung eines
Plattenkondensators mit Dielektrikum
elektrische Feld in beiden Fällen im Dielektrikum reduziert. Durch Polarisation wird ein Gegenfeld erzeugt, welches das elektrische Feld überlagert. Dieser Polarisationseffekt ist bei einem Dielektrikum aus
Aluminiumoxid
𝐶
𝐸 (1)
𝐸 (2)
𝐸 (3)
4,167 · 10−12 F
235,3 V/m
29,4 V/m
235,3 V/m
Teflon
𝐶
𝐸 (1)
𝐸 (2)
𝐸 (3)
3,54 · 10−12 F
200,0 V/m
100,0 V/m
200,0 V/m
Tabelle 2. Ergebnisse der analytische Berechnung eines
Plattenkondensators mit Dielektrikum
Aluminiumoxid deutlich stärker als bei Teflon, da dessen Dielektrizitätszahl viermal größer ist. In den
Abbildungen 8 und 9 sind die beiden elektrischen Felder noch einmal grafisch dargestellt. Die Pfeile zeigen
die elektrische Feldstärke an, sie sind auf die Länge eins normiert. Von
𝑥 = 11 mm bis 𝑥 = 21 mm handelt
es sich um das Dielektrikum aus Aluminiumoxid bzw. Teflon. Hier sind die Pfeile deutlich kürzer als in
den beiden anderen Gebieten mit dem Medium Luft. Da das elektrische Feld im Dielektrikum geschwächt
wird, erhöht sich gleichzeitig die Kapazität des Plattenkondensators.
12
11
10
9
8
y [mm]
7
6
5
4
3
2
1
0
0
5
10
15
z [mm]
20
25
30
Abbildung 8. Elektrisches Feld des Beispielplattenkondensators mit Aluminiumoxid
11
10
9
8
y [mm]
7
6
5
4
3
2
1
0
0
5
10
15
z [mm]
20
25
30
Abbildung 9. Elektrisches Feld des Beispielplattenkondensators mit Teflon
13
4
Numerische Simulation
Numerische Simulationen sind computergestützte Simulationen, die auf numerischen Verfahren beruhen.
Sie ermöglichen die Berechnung von komplexen physikalischen Systemen, die analytisch nicht mehr zu bewältigen sind. Problematisch sind die hohe Komplexität der Simulationsprogramme sowie die Unsicherheit
der gewählten Parameter. Die Simulationsergebnisse sollten daher immer durch analytische Überlegungen
oder reale Tests verifiziert werden.
Ein weit verbereitetes numerisches Simulationsverfahren ist die Finite-Elemente-Methode zur Lösung
von partiellen Differentialgleichungen. Dabei wird das Berechnungsgebiet in eine beliebige Anzahl von
Elementen aufgeteilt, welche sich durch eine endliche Anzahl von Parametern beschreiben lassen. Für
jedes Element werden anschließend Ansatzfunktionen aufgestellt. Deren Linearkombination, eingesetzt in
die Differentialgleichung des physikalischen Problems, ergibt zusammen mit Anfangs-, Rand- und Übergangsbedingungen das zu lösende Gleichungssystem. Materialgesetze berücksichtigen die vorliegenden
Stoffeigenschaften.
Die Genauigkeit der Finite-Elemente-Methode hängt stark von der Anzahl der Elemente ab, jedoch erhöht
sich auch der Rechenaufwand entsprechend. Je nach Anzahl der Unbekannten werden daher unterschiedliche Lösungsverfahren (Solver) eingesetzt. Bei kleinen Gleichungssystemen können direkte Lösungsverfahren verwendet werden. Bei sehr vielen Unbekannten muss aufgrund der schlechten Konditionierung
des Problems auf andere Verfahren, z. B. iterative Lösungsverfahren, zurückgegriffen werden.
4.1
Randbedingungen
Wie bereits im vorherigen Abschnitt beschrieben, werden für die Formulierung des zu lösenden Gleichungssystems Randbedingungen benötigt, sie müssen auf dem Rand des Definitionsbereichs vorgegeben
werden.
Eine Möglichkeit sind Neumann-Randbedingungen:
∮︁
∇𝜙 · 𝑛 d𝐴.
𝜕𝑉
In diesem Fall werden Werte für die Normalableitung des skalaren Potentials
𝜙
vorgegeben.
Dirichlet-Randbedingungen sind eine weitere Möglichkeit. Dabei werden Lösungswerte für das skalare
Potential
𝜙
direkt vorgegeben, welche auf dem Rand des Definitionsgebiets angenommen werden sollen.
Um auch das elektrische Feld außerhalb des Plattenkondensators zu berücksichtigen, muss das Rechengebiet bei der numerischen Simulation entsprechend über den Plattenkondensator hinaus vergrößert werden.
4.2
Schwache Formulierung
Elektrostatische Probleme können durch die Poisson-Gleichung
∇ · 𝜀∇𝜙 = −𝑞F
oder durch die Laplace-Gleichung
∇2 𝜙 = 0
14
beschrieben werden. Ein möglicher Lösungsansatz für die Klassen der beiden Feldgleichungen ist die
sogenannte schwache Formulierung. Ausgehend von der Poisson-Gleichung, erhält man nach der Multiplikation mit einer Testfunktion
𝛿𝜙
folgenden Ausdruck:
𝑞F
𝜕2𝜙
𝛿𝜙 = − 𝛿𝜙,
2
𝜕𝑥𝑖
𝜀
wobei
𝜀
homogen ist. Es folgt die Anwendung der Produktregel rückwärts
𝜕
𝜕𝑥𝑖
(︂
)︂
𝜕𝜙 𝜕𝛿𝜙
𝜕𝜙
𝜕2𝜙
𝛿𝜙 +
𝛿𝜙 =
,
𝜕𝑥𝑖
𝜕𝑥2𝑖
𝜕𝑥𝑖 𝜕𝑥𝑖
mit anschließender Integration:
∫︁
−
𝜕
𝜕𝑥𝑖
(︂
)︂
∫︁
∫︁
𝜕𝜙
𝑞F
𝜕𝜙 𝜕𝛿𝜙
𝛿𝜙 d𝑉.
𝛿𝜙 d𝑉 +
d𝑉 =
𝜕𝑥𝑖
𝜕𝑥𝑖 𝜕𝑥𝑖
𝜀
𝑉
𝑉
𝑉
Unter Berücksichtigung des Satzes von Gauß ergibt sich die schwache Formulierung zu
∮︁
−
𝜕𝜙
𝛿𝜙 d𝐴 +
𝜕𝑛
∫︁
𝜕𝜙 𝜕𝛿𝜙
𝑞F
d𝑉 =
𝜕𝑥𝑖 𝜕𝑥𝑖
𝜀
𝑉
𝜕𝑉
∫︁
𝛿𝜙 d𝑉.
𝑉
Im Falle der Laplace-Gleichung, folgt mit
∮︁
𝑞F = 0 und 𝜀 = homogen:
∫︁
𝜕𝜙 𝜕𝛿𝜙
𝜕𝜙
𝛿𝜙 d𝐴 −
d𝑉 = 0.
𝜕𝑛
𝜕𝑥𝑖 𝜕𝑥𝑖
𝜕𝑉
𝑉
𝜕𝜙
𝜕𝑛 ist die Ableitung von 𝜙 in Normalenrichtung der Fläche (nach außen). Die Testfunktion
den Randflächen verschwinden, wo 𝜙 vorgegeben ist.
𝛿𝜙
muss auf
Neben dem Vorhandensein der Neumann-Randbedingung in der Problemformulierung ist die Reduzierung der Ableitungsordnung eine weitere vorteilhafte Eigenschaft der schwachen Formulierung, da so
numerische Kosten eingesparrt werden können.
4.3
Netzgenerierung mit Gmsh
Für die Netzgenerierung wird das Programm Gmsh verwendet. Es hat einen großen Funktionsumfang
und besteht aus vier Modulen: Definierung von Geometrien, Netzgenerierung, das Lösen des Systems
und Post-Processing. Im Rahmen dieses Projektes wurden nur die ersten beiden Module verwendet.
Abb. 10 zeigt auf der linken Seite das fertig generierte Netz für einen Plattenkondensator mit einem
Dielektrikum zwischen den Platten. Wie man sieht, ist die Diskretisierung um den Mittelpunkt der Kugel
sehr fein. Zum äußeren Rand hin wird sie linear zum Radius immer gröber. Auf der rechten Seite der
Abbildung ist das Kugelinnere im Zweidimensionalen ohne generiertes Netz dargestellt. Die blau und
grün dargestellten Linien bilden die Platten des Kondensators. Um keinen Fehler bei der Netzgenerierung
zu erzeugen, müssen die beiden Linien Teil eines Körpers sein. In diesem Fall sind sie Seiten zweier
Rechtecke. Zwischen den Kondensatorplatten befindet sich, ebenfalls als Rechteck, das Dielektrikum. Die
gesamte Anordnung ist von einem Kreis eingeschlossen. Dieser hat physikalisch gesehen keine Bedeutung,
sondern dient als Hilfskonstrukt für die Netzgenerierung. Innerhalb des Kreises ist die Netzdiskretisierung
sehr fein, außerhalb wird sie immer gröber. Somit ist sichergestellt, dass das interessante Gebiet um die
Kondensatorplatten und im Volumen zwischen den Platten hoch aufgelöst wird. Der eigentliche Rand des
Berechnungsgebiets, ebenfalls eine Kugel, wird auf der rechten Seite nicht dargestellt.
15
grobes Netz
feines Netz
φ
1
Dielektrikum
φ
2
Abbildung 10. Netzgenerierung mit Gmsh
Die Bemaßungen der wichtigsten Elemente, wie die Radien der Kugeln, die Größe der Kondensatorplatten
und des Dielektrikums und der Grad der Diskretisierung, sind im Gmsh-Modell parametrisiert. Somit
kann das Modell zwischen den einzelnen Berechnungen schnell angepasst werden, was z. B. bei einer
Parameterstudie nützlich ist.
16
5
Ergebnisse
Für die numerischen Berechnungen wurden Neumann-Randbedingungen auf dem gesamten Rand des
Rechengebiets angenommen (𝜕𝜙/𝜕𝑛
= 0). Dies führt zu wesentlich realistischen Ergebnissen als die Wahl
einer Dirichlet-Randbedingung und wurde deswegen vorgezogen. Physikalisch gesehen lassen sich die
Neumann-Randbedingungen ebenfalls erklären, da der elektrische Fluss im Unendlichen verschwinden
muss. Die Rechengebiete sind kugelförmig, wie im Abschnitt „Netzgenerierung mit Gmsh“ beschrieben.
Allerdings konnten wir keine qualitativen Unterschiede zu einem quaderförmigen Rechengebiet feststellen. Abb. 11 zeigt das Ergebnis einer numerischen Feldberechnung eines Plattenkondensators mit einem
Abbildung 11. Feldberechnung eines Plattenkondensators mit Dielektrikum
Abbildung 12. Verlauf des E-Felds in einem Plattenkondensator mit Dielektrikum
Teflon-Dielektrikum
𝜀𝑟 = 2
und zwei Luftspalten. Wie auch bei der analytischen Berechnung ist eine
17
Reduzierung des elektrischen Feldes im Bereich des Dielektrikums gut zu erkennen. Am Rand der Kondensatorplatten kann man die Randeffekte sehen, ebenso wie die Feldlinien außerhalb des Kondensators.
Letztere Beobachtungen zeigen, wie groß die Vereinfachungen bei der analytischen Betrachtung sind.
Abb. 12 zeigt den Verlauf des elektrischen Feldes zwischen den Kondensatorplatten in z-Richtung. Die
Werte bestätigen die Beobachtung aus Abb. 11 und stimmen mit der analytischen Berechnung überein.
In Abb. 13 ist die Ablenkung der elektrischen Feldlinien im Umfeld eines kugelförmigen Dielektrikums
zu sehen. Abb. 14 zeigt, dass die numerischen Berechnungen diesen Effekt ebenfalls richtig wiedergeben.
Die Berechnungen haben gezeigt, dass die Stärke der Umlenkung der elektrischen Feldlinien von der Dielektrizitätskonstante abhängen. Je höher
Dielektrikum ein
𝜀𝑟
gleich 2.
𝜀𝑟
ist, desto größer ist die Auslenkung. Auf dem Bild hat das
Zusammenfassend kann man sagen, dass die analytischen Betrachtungen,
Ea
z
Abbildung 13. Kugeldielektrikum im ebenen E-Feld nach [Wolff, 1997]
trotz starker vereinfachender Annahmen, den Verlauf der elektrischen Feldstärke zwischen den Kondensatorplatten gut wiedergeben. Sie stimmen mit unseren numerischen Berechnungen überein und zwar
auch bei unterschiedlich geformten Dielektrika. Allerdings sind die gesamten Kondensator-DielektrikaKonfigurationen sehr einfach gehalten. Bei komplexeren Strukturen ist eine analytische Feldberechnungen
nicht mehr so einfach durchzuführen oder vollkommen ungeeignet.
Im Rechenvolumen außerhalb des Kondensators und auch an den Kanten der Kondensatorplatten stimmen die Ergebnisse gut mit den Ergebnissen aus der Literatur überein, was für die Auswahl der Neu-
mann-Randbedingung spricht. Der Radius der äußeren Kugel ist ebenfalls groß genug, sodass der Rand
als unendlich weit entfernt angenommen werden kann, ohne die numerischen Berechnungen merklich zu
beeinflussen.
18
Abbildung 14. Numerische Berechung eines Plattenkondensators mit kugelförmigem Dielektrikum
19
Literatur
Elektromagnetische Felder: Theorie und Anwendung. Springer, 2007.
H. Lindner and W. Siebke. Physik für Ingenieure. Physik für Ingenieure. Fachbuchverl. Leipzig im
1. Heino Henke.
2.
Carl-Hanser-Verlag, 1992.
Streifzüge durch die Kontinuumstheorie. Springer, 2011.
I. Wolff. Maxwellsche Theorie, Grundlagen und Anwendungen. Springer, 1997.
3. Wolfgang H. Müller.
4.
20
Anhang
Listing 1. Plattenkondensator/Dielektrikum mit Fenics
from
dolfin
import numpy
import
as
*
np
parameters [ " form_compiler " ] [ " cpp_optimize " ]
parameters [ ’ form_compiler ’ ] [ ’ o p t i m i z e ’ ]
= True
= True
parameters [ " form_compiler " ] [ " r e p r e s e n t a t i o n " ]
= " quadrature "
parameters [ " form_compiler " ] [ " quadrature_degree " ]
= 2
#=====================================
#
Mesh
#=====================================
mesh = Mesh ( " m s p h e r e . xml " )
n = F a c e t N o r m a l ( mesh )
subdomains = MeshFunction ( " s i z e _ t " ,
mesh ,
" m s p h e r e _ p h y s i c a l _ r e g i o n . xml " )
b o u n d a r i e s = MeshFunction ( " s i z e _ t " ,
mesh ,
" m s p h e r e _ f a c e t _ r e g i o n . xml " )
dV = M e a s u r e ( " dx " ) [ s u b d o m a i n s ]
dAo = M e a s u r e ( " d s " ) [ b o u n d a r i e s ]
dAi = M e a s u r e ( " dS " ) [ b o u n d a r i e s ]
# Surfaces :
#
dAo(122)
#
dAi (117)
#
dAi (118)
#
dAi (119)
#
dAi (120)
#
dAi (121)
# Volumes :
#
dV(218)
#
dV(216)
#
dV(217)
#
dV(219)
#
dV(120)
# Function space
outer sphere
capacitor top plate
capacitor bottom plate
d i e l e c t r i c top
d i e l e c t r i c bottom
d i e l e c t r i c sides
dielectric
capacitor top
capacitor bottom
inner sphere
outer sphere
S p a c e = F u n c t i o n S p a c e ( mesh ,
’ Lagrange ’ ,
1)
# Functionsraum fuer skalare Materialkonstanten
KSS = F u n c t i o n S p a c e ( mesh ,
"DG" ,
# Constants
eps_0 = 8 . 8 5 4 2 * pow ( 1 0 , − 12)
#eps_r = 8.0 # Glas
eps_r = 2 . 0
# Gummi
#eps_r = 80.0 # dest . Wasser
#eps_r = 1.5
0)
21
# Functions
e p s = F u n c t i o n ( KSS )
phi = Function ( Space )
del_phi = TestFunction ( Space )
t r i a l _ p h i = T r i a l F u n c t i o n ( Space )
# DirichletBoundaryConditions
p h i 1 = D i r i c h l e t B C ( Space ,
Constant ( 0 . 0 ) ,
boundaries , 2 1 0 )
p h i 2 = D i r i c h l e t B C ( Space ,
Constant ( 5 . 0 ) ,
boundaries ,
BCS =
[ phi1 ,
# Equations
V0 = eps_0
*
212)
phi2 ]
i n n e r ( grad ( t r i a l _ p h i ) ,
V1 = eps_0 * e p s _ r
*
g r a d ( d e l _ p h i ) ) * ( dV ( 2 1 6 ) + dV ( 2 1 7 ) + dV ( 2 1 9 ) + dV ( 2 2 0
i n n e r ( grad ( t r i a l _ p h i ) ,
grad ( del_phi ) )
*
dV ( 2 1 8 )
F = V0 + V1
a,
L = l h s (F ) ,
s o l v e ( a == L ,
# Phi
fileV
r h s (F)
phi ,
b c s=BCS ,
s o l v e r _ p a r a m e t e r s ={" l i n e a r _ s o l v e r " :
= F i l e ( ’ p h i . pvd ’ )
f i l e V << p h i
# E−Feld
VSpace = V e c t o r F u n c t i o n S p a c e ( mesh ,
E = a s _ t e n s o r (−
p h i . dx ( i ) ,
Epro = p r o j e c t ( E ,
fileE
[ i ])
VSpace )
= F i l e ( ’ E . pvd ’ )
f i l e E << Epro
# D−Feld
D = a s _ t e n s o r (−
p h i . dx ( i ) * e p s ,
Dpro = p r o j e c t (D,
VSpace )
f i l e D = F i l e ( ’D . pvd ’ )
f i l e D << Dpro
[ i ])
’ Lagrange ’ ,
1)
" gmres " } )