D - photonik

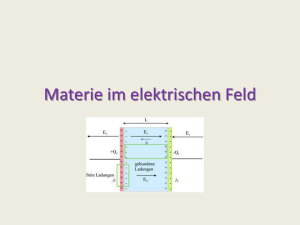
1.9 Dielektrika im elektrostatischen Feld
Dielektrika = Isolatoren: Elektronen fest an Atomrümpfe gebunden
Auswertung des Kondensatorexperiments
-σ
++Dielektrikum
++-
σ +
+
+
+
+
+
Wenn U fällt muss auch E kleiner werden!
⇒ im Dielektrikum wird eine Ladungsdichte
induziert:
σP
1
- -
E
+
-
- -
- - - - - + - - - - - - -
Das Feld verschiebt die Ladungsschwerpunkte
der atomaren Ladungen.
Im Inneren des Dielektrikums kompensieren
sich positive und negative Ladungen.
Es entstehen atomare Dipole in E-Richtung:
p = qd
An den Oberflächen bilden sich Polarisationsladungsdichten.
-σ σP
-σP σ
Polarisation:
Diese generieren ein
Feld EP=σP/ε0.
+- +- ++- +- ++- +- ++- +- +d
σP =
QP N ⋅ q ⋅ d ⋅ A
=
= N ⋅ p = P ⇒ Die Polarisation ist das Dipolmoment
pro Volumeneinheit (Dipoldichte)
A
A
2
Elektrische Verschiebung
D/ε0 ist also das E-Feld ohne Dielektrikum.
Mit diesen Definitionen folgt
E ist das messbare Feld, das auf Probeladung im Dielektrikum wirkt.
Annahme: Wirkung (P) ist der Ursache (E) proportional
χ: Suszeptibilität
Erfahrung: Richtig solange E nicht zu groß wird (E LAtom<< WAtom) !
3
oder
Dielektrizitätskonstante (DK)
ε und χ sind Materialparameter.
E im Dielektrikum ist um den Faktor 1/ε kleiner als im Vakuum,
ebenso U.
⇒ Die Kapazität des Kondensators steigt
um den Faktor ε.
4
Einhomogen
A +
- -+
+
+
- ++
- + V
-
Allgemein:
ε>1
∆Qpol = ∫ ρ pol dV = − ∫ σ pol dA = − ∫ Pd A
V
A
∫ Pd A = ∫ div PdV
A
div E =
A
div P = − ρ pol
V
1
ε0
( ρ + ρ pol )
mit
E = ( D − P) / ε 0
5
Elektrostatische Maxwell-Gleichung im Medium
Außerdem muss immer die Zirkulation verschwinden.
Beachte: ρ = „Überschußladungen“ (z.B. auf den Kondensatorplatten), ohne solche Ladungen im Dielektrikum ist
div D = 0.
Die DK kann von der Richtung im Dielektrikum abhängen, sie kann
eine orts- und/oder zeitabhängige Retardierung beschreiben.
6
Brechungsgesetz für Feldlinien
A D
Tangentialkomponenten
En(1)
Et(1) E(1) θ
1
B C
Wegunabhängigkeit der Arbeit:
En(2)
θ2
Et(2) E(2)
B
∫ Ed s = 0 = ∫ E
A
ε=1
t
(1)
D
d s1 + ∫ E t d s 2
( 2)
C
ε>1
⇒
7
Normalkomponenten
Dn „sieht“ Grenzfläche nicht:
Dn(1)
Dt(1) D(1) θ
1
Dn
(2)
θ2
Dt(2) D(2)
ε=1
∫ Dd A = ( Dn − Dn )∆A = 0
(1)
( 2)
A
⇒
ε>1
mit E(1)sin θ1 = E(2)sin θ2 und E(1)cos θ1 = εE(2)cos θ2
Brechungsgesetz für Feldlinien:
FL:
Brechung vom Lot weg.
8
Die elektrische Feldenergie im Dielektrikum
1
1
A 2 2
2
Wel = CU = εε 0 d E
2
2
d
Energiedichte ωel = Wel/V:
Beachte: Es gilt
diel
el
w
=
1
ε
1
1 1 2
2
wel = εε 0 E =
D
2
2 εε 0
welvac < welvac
Allgemein gilt für die Energiedichte im Medium:
1
wel = ED
2
9
ωpol für N induzierte Dipole pro Volumeneinheit:
d
kx = qE
wPol
W pol
1 2 1
1
= ∫ Fdx = kd = qdE = pE
2
2
2
0
1
1
1
= NpE = PE = ε 0 (ε − 1) E 2
2
2
2
∆wel = wel
diel
− wel
vac
= wpol
Energieänderung rührt von der Polarisation des eingebrachten
Mediums her.
10
Kräfte auf das Dielektrikum
Die Feldenergie im Kondensator W = Q2/2C = CU2/2 nimmt
durch Dielektrikum um Faktor 1/ε ab.
⇒ Ein Dielektrikum wird in den Kondensator hineingezogen!
+ + +++++++
F
+
+
+
- - -------
11
dA
Änderung um dz
AO
d
dz
Ao: Querschnitt an dem Kraft ansetzt
Also Zugspannung
12
Bestimmung der Dielektrizitätskonstante
U
Steighöhe
d
h
Bestimmung von ε
13
Bisher: Dielektrika (ohne E keine Dipole)
Paraelektrika besitzen permanente
Dipole, die im Feld ausgerichtet
werden.
1
P=
V
∑p
i
pE
ν=
3kT
Np 2
P=
E
3kT
P
Np 2
ε −1 =
=
ε 0 E 3ε 0 kT
14
Ferroelektrika: Permantente Dipole, Festkörper, Bsp. BaTiO3
ohne Feld:
P≠0
für T < TC
P(E) Hysterese
Ursache: Dipol-Dipol-Wechselwirkung
Piezoelektrika: Mechanische Spannung erzeugt P
Pyroelektrika: Erwärmung erzeugt P
15