Materie im elektrischen Feld

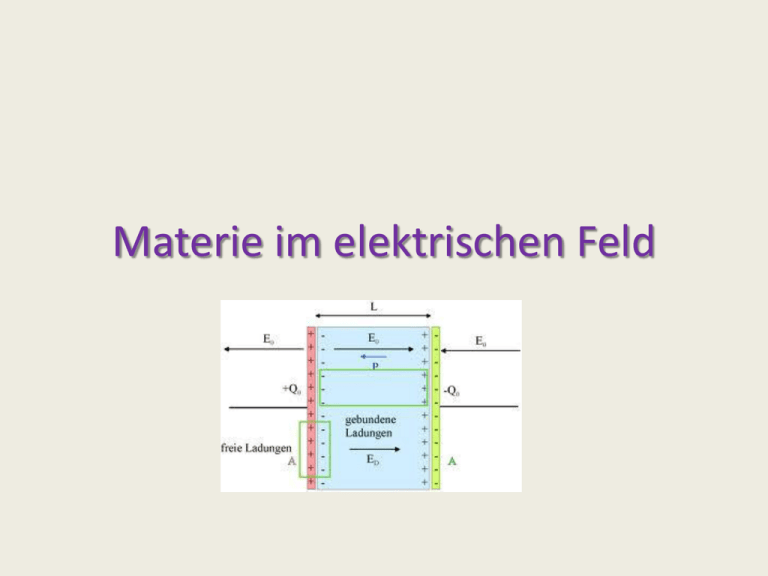
Materie im elektrischen Feld
Elektrische Leiter im elektrischen Feld
Definition: Ein Medium heißt elektrischer Leiter, wenn Ladungsträger
frei (ohne Kraftaufwand) verschiebbar sind.
Beispiele:
Supraleiter, Metalle (annähernd), astrophysik. Plasmen (annähernd)
Folgerung: In statischer Situation verschwindet im Innern eines
elektrischen Leiters überall das elektrische Feld.
 
Beweis: Wäre irgendwo E  0 , würde
 aufdie dort lokalisierten freien
Ladungsträger q die Kraft F  q E wirken
 Ladungsverschiebung
 Widerspruch zur Annahme einer statischen Situation.
Influenz
Externes Feld


E ext  0
Beispiele:


E
-
LadungsVerschiebung







 
E0


E tot  0
Gegenfeld
im Leiter

E


-
- 
- 


 
E0

Folgerungen:
 
a) E  0 im Inneren

Ladung nur auf Leiteroberfläche

b) statische Situation  E  Oberfläche
 Oberfläche  Äquipotentialfläche


F||  q E||

E

E ||

E
.
-
q
Leiter
c) In zusammenhängenden Leitern gilt
  const.
d) Faraday-Käfig:
Potential im Innenraum:
  0
Randbedingung (Innenwand):
 Wand  0  const.
Vakuum   0
  0  const.


Folgerung: E
0
Lösung:
Innenraum
e) Netzkäfige, Lochdimension d:
Durchgriffslänge des E-Feldes ist O(d)
Grund: d ist einzige Längenskala des
Problems
geschlossene
Leiterwand
d
Plattenkondensator
+Q

E
Q
A
0
homogen
in Praxis: A  d2
U  1  2
1
U
E
d
2
d
x
U
σ
Q
E 
d
ε0 ε0 A
A
Q  ε0  U
d
A
C  ε0 
d
Plattenkondensator
U
 homogener
Bereich
komplizierte
Randeffekte
Parallelschaltung:
C1
Q1
0V
C2
Q2
C3
U
U  U1  U 2  U3  
Q  Q1  Q2  Q3  
Q3
Q Q1 Q 2 Q3
Q1 Q 2 Q3
C 


 



U U U U
U1 U 2 U 3
C  C1  C2  C3  
Serienschaltung:
U
U1
U2
U3
C1
C2
C3
Q
Q
Q
Q
Q  Q1  Q2  Q3  
Q
0V
Q
U  U1  U 2  U3  
1 U U1 U 2 U 3
U1 U 2 U 3
 


 



C Q Q Q Q
Q1 Q 2 Q3
1 1
1
1




C C1 C 2 C3
Dielektrika
Keine frei beweglichen Ladungstrager
Dielektrika
Statische elektrische Felder in Materie

E
a) polare Dielektrika: z.B. Wasser
permanente molekulare Dipole
Ausrichtung  starkes Gegenfeld
b) nicht-polare Dielektrika:
induzierte molekulare Dipole: „Polarisation”
⊕ Atomkerne
⊝ Elektronenwolke der Atomhüllen
Polarisation  Gegenfeld, oft  E

E



Molekülpolarisation: molekulares Dipolmoment p


1
Polarisationsdichte: P 
pi

ΔV ΔV
ρ tot ρ  ρ pol

ε0
ε0
Überschussladung: Q

E
Def.: Dielektrische Verschiebung

 
D  ε0 E  P
V
(Materialgleichung)
Polarisationsladung: Qpol


Lineare Näherung: p  α  E

α  const. bis typisch E  105 V cm
(molekulare) Polarisierbarkeit
 
 dN


 P
 α  E  χ e  ε0 E
dV
dielektrische Suszeptibiliät

 


 D  ε 0 E  P  1  χ e ε 0 E  ε ε 0 E
relative Dielektrizitätskonstante:
ε  εr  1  χ e
isotropes Medium
  Zahl (Skalar)
anisotropes Medium   Tensor (2. Stufe)
Faustregel: Für homogene isotrope Medien ersetzen in allen
Formeln für das Vakuum einfach 0 durch 0.
Beispiel: Kondensator mit Dielektrikum
A
Q  C  U mit C  ε ε0  ε
d
1
Q fest  U 
ε

U fest  Q  ε
d

E
A

Feldenergie:
1
1
A
1
2
2
W  CU  ε ε 0 Ed   V E D
2
2
d
2
 
w  12 E  D
(gilt auch allgemein)
z

Dielektrikum
(Isolator, große Polarisierbarkeit)