28. Isolatoren im elektrischen Feld

Elektrizitätslehre – Isolatoren im elektrischen Feld
28.
Isolatoren im elektrischen Feld
28.1.
Die Verschiebungsdichte
−
Es existieren zwei Arten der Beziehung elektrisches Feld ↔ Ladung:
a) Das Feld wird von Ladungen erzeugt. Die Ladungen sind Quellen/Senken
des Feldes („Feldlinien kommen aus Ladungen heraus bzw. gehen hinein“).
!
Die Quelldichte des Feldes wird durch die Divergenz charakterisiert:
r 1
div E = ⋅ ρ
ε0
dQ
ρ=
... Ladungsdichte
dV
b) Das Feld übt auf Ladungen Kräfte aus:
r
r
F = Q⋅E
−
(25 - 20)
!
(25 - 4)
r
In b) ist E direkt enthalten, in a) mit der Proportionalitätskonstante ε0.
Es ist zweckmäßig, eine weitere elektrische Feldgröße zu definieren, die in a)
ohne Proportionalitätskonstante auskommt und dafür eine in b) hätte.
r
Dies ist die sogenannte Verschiebungsdichte D mit
r
div D = ρ
(1)
r
r
r
D ist ein Vektorfeld wie E , an jedem Punkt r ist
r r
r r
E ( r ) ~ D( r )
Offenbar gilt (zumindest im Vakuum1)
r
r
D = ε0 ⋅ E
Kommentar:
(2)
u
Feldstärke und Verschiebungsdichte sind zwei Größen zur Beschreibung des
elektrischen Feldes. Der Vorteil der neuen Größe wird erst beim Isolator im
elektrischen Feld deutlich werden.
1
Mit elektrischen Feldern in Stoffen haben wir uns ja bisher nicht befasst. Das Problem „Leiter und
elektrisches Feld“ (vgl. <27.>) bringt in dieser Hinsicht noch nichts, denn wir haben gesehen, dass
r r
in Leitern E = 0 ist.
30
Elektrizitätslehre – Isolatoren im elektrischen Feld
28.2.
Einige grundlegende Experimente
a) Aufladen eines (z.B.) Bernsteinstabes
durch Reiben mit (z.B.) Katzenfell und
Heranbringen von Holundermarkkügelchen in die Nähe des Stabes
·
·
Bildung eines induzierten Dipolmomentes im Kügelchen
Anziehung des Dipols im inhomogenen Feld des Stabes (vgl. <25.4.>)
b) Aufstellen einer geerdeten Metallplatte
zwischen Stab und Kügelchen
·
·
·
Ansammlung positiver Ladungen an der Metall-Oberfläche (Influenz)
der Raum hinter der Platte ist feldfrei; der Leiter schirmt das Feld ab
Es erfolgt keine Anziehung des Kügelchens mehr!
c) Aufstellen einer Isolatorplatte zwischen Stab und Kügelchen
·
Das Kügelchen wir angezogen! ⇒ Das elektrische Feld greift durch den
Isolator durch.
⇒ Ein Isolator wird auch als Dielektrikum bezeichnet1.
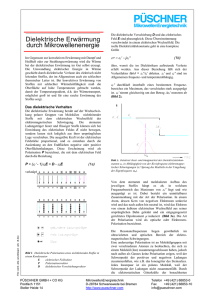
d) Isolator im Plattenkondensator
1.) Der Plattenkondensator wird leer (d.h. mit Luft zwischen den Platten) mittels einer äußeren Spannung aufgeladen. Es fließt die Ladung
Q = C⋅U =
A ⋅ ε0
⋅U
d
(27 - 9)
auf ihn.
1
dia... (in Zusammensetzungen) - hindurch (griech.)
31
Elektrizitätslehre – Isolatoren im elektrischen Feld
2.) Der Kondensator wird von der Spannungsquelle getrennt
3.) Es wird ein Dielektrikum in den Zwischenraum gebracht.
Die Spannung U verringert sich auf
U
ε
(ε > 1)
An der Ladungsbelegung der Platten (± Q) hat sich jedoch nichts geändert,
denn bei Entfernen des Dielektrikums steigt U wieder auf den alten Wert!
−
Die Definition der Kapazität C = Q / U lt. Gl. (27- 7) gilt allgemein. Wenn
also U bei konstantem Q sinkt, muss sich C erhöht haben:

ohne Dielektrikum 

(„Vakuum“)


U
C
→
→
U
ε
ε⋅C





mit Dielektrikum
−
Technische Kondensatoren haben ein Dielektrikum mit großem ε.
−
Man benutzt die Änderung der Kondensatorkapazität, um die Materialkonstante ε zu definieren: Die Dielektrizitätskonstante ε eines Materials ist das
Verhältnis der Kapazität eines Kondensators mit diesem Material im Zwischenraum bzw. ohne:
ε=
C
C Vak
!
(3)
Aufgrund dieser Definition ist die Dielektrizitätskonstante dimensionslos.
Beispiele:
Material
Glas
Gummi
Ethylalkohol
Wasser
Luft
Dielektrizitätskonstante
5 - 10
2,5 - 3,5
25,8
(20 °C)
81,1
(18 °C)
1,0006
( 0 °C, 1 atm)
æ
≈ Vakuum!
n
32
Elektrizitätslehre – Isolatoren im elektrischen Feld
−
Schlussfolgerung:
Wenn der Kondensator erst nach dem Einschieben des Isolators von der
Spannungsquelle getrennt wird, fließt eine größere Ladung auf die Platten:
Q
å
C vak ⋅ U
28.3.
−
→
ε⋅Q
æ
C ⋅ U = ε ⋅ C Vak ⋅ U
Interpretation der Ergebnisse
Wenn in Experiment d) die Spannung sinkt, muss sich die elektrische Feldstärke reduziert haben, denn im homogenen Feld des Plattenkondensators gilt ja (vgl. <27.3.>)
r U
E=
d
d ... Plattenabstand
(4)
r
Wegen Gl. (4) reduziert sich E genauso wie U.
Vakuum
−
...
r
E
→
1 r
⋅E
ε
...
mit Dielektrikum (ε)
Die Feldstärke im Plattenkondensator ohne Dielektrikum („Vakuum“) beträgt lt.
Gl. (27 - 8):
1 Q
⋅
ε0 A
â
(= Flächenladungsdichte σ)
E Vak =
Mit Dielektrikum reduziert sich die Feldstärke E um
E Diel =
−
(5)
1
:
ε
1 Q
⋅
ε ⋅ ε0 A
(6)
Wir erinnern uns, wie wir in
r
<27.3.> E Vak lt. Gl. (5) ermittelt hatten:
r
1
E
∫ ⋅ dA = ε 0 ⋅ Q ges, innerhalb d. Fläche A*
geschl. Fläche A*
(25 - 10)
Dies muss natürlich auch jetzt noch gelten! Aber das Integral über A* mit
Qges = „Q auf der Kondensatorplatte“ hatte eben in <27.3.> das EVak lt. Gl. (5)
ergeben und nicht EDiel lt. Gl. (6).
33
Elektrizitätslehre – Isolatoren im elektrischen Feld
−
⇒ Innerhalb von A* müssen weitere Ladungen sitzen, und zwar eine entgegengesetzte (hier: negative) Ladung QP (Polarisationsladung) auf
der Oberfläche des Dielektrikums.
!
r
Diese reduzieren das E -Feld im Isolator, das von Q - QP bestimmt wird.
!
r
r
Beschreibung des (reduzierten) E -Feldes E Diel im Innern des Dielektrikums:
Es ist gleichwertig, ob man
·
von Q ausgeht und über
·
Gl. (5) nimmt (ohne
E Diel =
1
reduziert gemäß Gl. (6), oder
ε
1
), aber mit der effektiven Ladung Q - QP
ε
1 Q 1 Q − QP
⋅ =
⋅
ε ⋅ ε0 A ε0
A
â
â
Gl. (6)
Gl. (5) mit effektiver Ladung
(7)
Umgeformt aus Gl. (7) erhält man:
Qp =
−
ε −1
⋅Q
ε
(8)
r
Wir definieren die dielektrische Polarisation P :
r Q
P= P
A
(9)
r
r
Die Richtung von P geht von -QP nach +QP, also dem E -Feld parallel gerichtet.
!
r
Man kann P als Dipolmoment pro Volumen deuten.
!
34
Elektrizitätslehre – Isolatoren im elektrischen Feld
Das Dipolmoment des polarisierten Dielektrikums ergibt sich zu
r
p = d ⋅ QP
Dieses Dipolmoment geteilt durch das
Volumen liefert:
Dipolmoment
á
r
p d ⋅ QP QP r
=
=
≡P
V A⋅d
A
â
Polarisation
−
(25 - 21)
Einsetzen von Gl. (8) in Gl. (9) liefert
r ε −1 Q
P=
⋅
ε A
−
mit
Q
= ε ⋅ ε 0 ⋅ E Diel
A
(6‘)
folgt:
r
r
r
P = (ε − 1) ⋅ ε 0 ⋅ E Diel = χ P ⋅ E Diel
χP ... dielektrische Suszeptibilität (Materialkonstante, gelegentlich genutzt)
(10)
Wir bilden nun mit Gl. (10)
r
r
r
r
P + ε 0 ⋅ E Diel = (ε − 1) ⋅ ε 0 ⋅ E Diel + ε 0 ⋅ E Diel
r
= ε ⋅ ε 0 ⋅ E Diel
r
r
ε ⋅ E Diel = E Vak
r
r
= ε 0 ⋅ E Vak ≡ D
⇒
(11)
Gl. (11) ist die Verallgemeinerung von Gl. (2). Es gilt also:
r
Wenn ein Dielektrikum existiert, entsteht eine dielektrische Polarisation P und
r
r
das elektrische Feld E reduziert sich zu E Diel . Im Vakuum gibt es keine Polarir
sation und das elektrische Feld E ist entsprechend größer.
!
⇒ Wir können allgemein schreiben:
r
r r
P + ε0 ⋅ E = D
(12)
35
Elektrizitätslehre – Isolatoren im elektrischen Feld
Veranschaulichung:
Kommentar:
r
·
P zeigt von - nach + (entsprechend der Definition des Dipolmomentes!).
r
·
E muss mit ε0 „geeicht“ werden.
r
·
D „geht durch den Isolator hindurch“1, je nach ε ändert sich nur das Verr
r
hältnis von E zu P .
u
r
Wichtig: Kräfte auf bzw. zwischen Ladungen hängen vom E -Feld ab, sie sind
daher in Dielektrika geschwächt.
−
n
Beispiel: Wasser
Die Wechselwirkung der Ionen in Wasser (ε = 81,1) ist nur 1/ε ≈ 1,2 % so groß wie wenn
die Ionen den gleichen Abstand im Vakuum hätten. Dadurch wird die Dissoziation von
Verbindungen in Wasser sehr erleichtert, die thermische Energie reicht schon!
28.4.
Mechanismen der dielektrischen Polarisation
Frage danach, wie die Oberflächenladungen ±QP auf dem Dielektrikum zu Stande kommen können
=
Es gibt zwei Möglichkeiten der Entstehung, die beide unter dem Einfluss eines
äußeren elektrischen Feldes stattfinden:
·
·
a)
Ausrichtung vorhandener (permanenter) Dipole, oder
Schaffung (Induzierung) von Dipolen
Induzierung von Dipolen (sogenannte Verschiebungspolarisation)
Es kommt zur Trennung der Ladungsschwerpunkte und Bildung eines Dipolr
momentes p .
!
⇒
1
Dies gilt streng nur für die Komponente senkrecht zur Oberfläche!
36
Elektrizitätslehre – Isolatoren im elektrischen Feld
einfache Modellvorstellung:
·
r
das äußere elektrische Feld E übt eine Kraft aus
F = Q⋅E
·
es existiert eine „elastische“ (lineare) Rückstellkraft
F = − k ⋅ ∆x
⇒
·
∆x =
Q⋅E
k
die Auslenkung ∆x bringt ein Dipolmoment zustande
r
p ≡ p = ∆x ⋅ Q
=
Q2
⋅E
k
p = α⋅E
α ... Polarisierbarkeit (Eigenschaft des Atoms)
·
(13)
r
Die Polarisation P war Dipolmoment pro Volumen, so dass mit der Teilchenzahldichte n = N / V (Teilchen pro Volumen) aus Gl. (13) folgt
r r
r
n ⋅p = n ⋅α⋅E = P
å
æ
Dipolmoment
Polarisation
eines Atoms
(14)
Vergleich von Gl. (14) mit Gl. (10) ergibt
(ε − 1) ⋅ ε 0 = n ⋅ α
(15)
Gl. (15) stellt eine Verknüpfung makroskopischer mit atomaren Größen dar!
Eine dielektrische Substanz haben wir uns etwa so vorzustellen:
Im Innern ist die Verschiebungspolarisation nicht zu spüren („was
A nach links geht, geht B nach
rechts“).
!
Was insgesamt bleibt, ist die Aufladung der Oberflächen (±QP)
37
Elektrizitätslehre – Isolatoren im elektrischen Feld
b) Ausrichtung vorhandener Dipole (sogenannte Orientierungspolarisation)
Manche Moleküle1 besitzen ein permanentes Dipolmoment, z.B. HF, HCl, oder H2O:
Im Allgemeinen sind die Dipolmomente infolge der Wärmebewegung regellos
ausgerichtet.
!
Durch ein äußeres elektrisches Feld kann eine Ausrichtung erfolgen.
!
u
Kommentar:
·
·
Die thermische Bewegung wirkt der Ausrichtung entgegen. Eine einigermaßen vollständige Ausrichtung ist nur bei großen Beträgen der elektrischen Feldstärke bzw. bei kleinen Temperaturen zu erwarten.
r
Bei einem E -Wechselfeld kann es durch ständiges Umorientieren zu Reibung und Wärmeentwicklung kommen (eher bei Flüssigkeiten, weniger bei
Gasen) ⇒ dielektrische Verluste.
Beispiel: Wasser im Mikrowellenherd
!
n
Es kann auch passieren, dass bei hohen Frequenzen die Moleküle dem Feld
infolge ihrer Trägheit nicht so schnell folgen können.
28.5.
−
Energiedichte des elektrischen Feldes im Dielektrikum
Die Energiedichte des elektrischen Feldes war im Vakuum
w=
W ε0 2
= ⋅E
V
2
(27 - 18)
Mit D = ε0 ž E gemäß Gl. (2) können wir schreiben
1
w = ⋅E⋅D
2
(16)
In dieser Form gilt die Gleichung ganz allgemein, auch in Dielektrika. Wir
müssen nur für D die bereits bekannte Form verwenden:
D = ε0 ⋅ ε ⋅ E
1
(11)
Solche Materialien werden als par(a)elektrisch bezeichnet.
38
Elektrizitätslehre – Isolatoren im elektrischen Feld
−
Bei der Betrachtung der Energiedichte muss man sorgfältig die konkreten physikalischen Bedingungen berücksichtigen, wie an folgenden Beispielen deutlich wird:
a)
Wir erinnern uns an das Experiment, in dem der aufgeladene Kondensator
von Spannungsquelle abgeklemmt war und ein Dielektrikum hinein- und
herausgeschoben wurde. Dabei blieben die Ladungen auf den Platten unverändert (Q = const.), d.h. D = const.:
·
Die Energiedichte mit Luft („Vakuum“) ist:
w=
·
1
⋅ E Vak ⋅ D
2
Mit Dielektrikum reduziert sich bei konstantem D die Feldstärke E auf
1
⋅ E Vak
ε
Für die Energiedichte mit Dielektrikum folgt:
w=
1 1
⋅ ⋅ E Vak ⋅ D
2 ε
⇒ Die Energiedichte w wird auf 1/ε reduziert, was einem Übergang in einen energieärmeren Zustand entspricht.
b) Der Kondensator bleibt an Spannungsquelle angeschlossen. Auch hier sinkt
zunächst durch das Einschieben des Dielektrikums die Feldstärke E
auf ε-1 ž EVak. Dann aber fließen solange Ladungen nach, bis Spannung und
Feldstärke wieder den alten Wert erreicht haben.
⇒ E bleibt unverändert, aber D ist durch zusätzliche Ladungen auf das ε-fache
D
angestiegen, da das Verhältnis
lt. Gl. (11) auch hier wieder stimmen muss.
E
·
Die Energiedichte mit Luft („Vakuum“) ist wiederum:
w=
·
1
⋅ E Vak ⋅ D
2
Für die Energiedichte mit Dielektrikum folgt:
1
w = ⋅ ε ⋅ E Vak ⋅ D
2
⇒ Die Energiedichte w wird bei gleicher Ladespannung des Kondensators
auf das ε-fache erhöht!
In technischen Kondensatoren werden Dielektrika mit großem ε verwendet.
!
39
Elektrizitätslehre – Isolatoren im elektrischen Feld
−
Schlussbemerkung:
Alle bisherigen Darlegungen gelten für den voll mit Dielektrikum erfüllten
(Platten-)Kondensator. Wenn man beliebig geformte dielektrische Körper in einen Kondensator hängt, kann es spezielle Effekte geben.
!
Plausibilitätserklärung:
dielektrischer Stab in einem Luftkondensator:
r
Das E -Feld zwischen den Polarir
sationsladungen wirkt voll E -Feldschwächend.
28.6.
r
Das E -Feld zwischen den Polarisationsladungen verläuft außerr
halb und wirkt dem E -Feld im
Material praktisch nicht entgegen.
Piezoelektrizität und Elektrostriktion; Ferroelektrizität
−
Bisher haben wir die Polarisation infolge eines äußeren elektrischen Feldes betrachtet.
−
Jedoch: Es existieren Festkörper, bei denen Polarisation durch elastische Verformung erzeugt werden kann (sogenannte Piezoelektrizität).
!
Paradebeispiel: Quarz (kristallines SiO2)
n
({2}, S. 88)
40
Elektrizitätslehre – Isolatoren im elektrischen Feld
−
Kommentar:
·
Ursache ist die sogenannte polare Achse im Kristall (in den Abbildungen
vertikal gezeichnet, d.h. X1-Achse)
·
Druck/Zug parallel zur polaren Achse bewirkt, dass positive (+) oder negative (-) Ladungen näher an die Oberfläche rücken als im Normalfall
·
Druck/Zug senkrecht zur polaren Achse bewirkt den analogen Effekt wegen
der Querkontraktion (vgl. <11.1.>)
u
Umgekehrt führt das Anlegen einer äußeren Spannung an einen solchen Kristall
dazu, dass sich dieser entsprechend verformt ⇒ Elektrostriktion
!
∆l
l
Piezoelekt
  rizität

→
←


Elektrostriktion
r
P
⇒
∆U
(Spannungsdifferenz zwischen den Oberflächen)
generell:
∆l
ist relativ klein (≤ 1 %)
·
l
·
∆U ist relativ groß (≈ kV)
Beispiel:
n
Das Anlegen einer Wechselspannung entsprechender Frequenz bewirkt eine Schallemission des Quarzes.
−
Vielfältige Anwendungen:
·
·
·
−
piezoelektrischer Gasanzünder (Druck ⇒ Funken)
piezoelektrisches Stellglied (elektrische Spannung ⇒ elastische Verformung, die zum Verstellen im Sub-Å-Bereich genutzt wird; sehr definiert,
ruck- und spielfrei) ⇒ Raster-Tunnel-Mikroskopie (STM) ermöglicht.
elektromechanischer Schwinger („Schwingresonanz“)
Der elektromechanische Schwinger ist das Analogon zum mechanischen
Schwinger mit seinem Wechselspiel zwischen kinetischer und potentieller
Energie (Ekin/Epot). Beim schwingenden Quarzkristall ist dies ebenso, aber
gleichzeitig kommt es dabei zu einem periodischen Umladen der Oberfläche! So ist die Kopplung eines Schwingquarzes mit einem elektrischen
Schwingkreis möglich. Maßgebend ist die mechanische Eigenfrequenz des
Quarzes, analog der eines Perpendikels). Anwendung: Quarzuhr
Ferroelektrizität: Manche Piezoelektrika haben auch im unverformten Zustand
schon eine Polarisation, d.h. „aufgeladene Oberflächen“.
·
·
!
formale Analogie zum Ferromagneten („ohne äußere Einwirkung bereits ...“)
Quarz ist streng genommen auch ein Ferroelektrikum, wird jedoch unter
realen Umweltbedingungen (adsorbierte Luftfeuchte) als solches nicht wirksam.
41
Elektrizitätslehre – Isolatoren im elektrischen Feld
n
Paradebeispiel: Bariumtitanat (BaTiO3)
!
Ba2+, Ti4+, O2-; TC = 120 °C
Erklärung:
„Für das relativ kleine Ti4+-Ion ist die
Gitterlücke zu groß. Es kann nicht in der
Mitte schweben und lehnt sich an eines
der 6 Sauerstoff-Ionen, das sich seinerseits disloziert.“
({3}, S. 619)
Kommentar:
·
Eigentlich existieren 6 gleichwertige Möglichkeiten der Ortsverlagerung des
Ti-Ions. Dies führt aber nicht dazu, dass sich die verschiedenen Verlagerungen regellos mischen und makroskopisch nichts wahrgenommen wird, sondern es besteht die Tendenz der Fortpflanzung der Polarisation über einen
größeren Bereich (ferroelektrische Domäne).
·
Oberhalb einer bestimmten Temperatur TC (CURIE-Temperatur) geht die
Ordnung verloren.
u
42