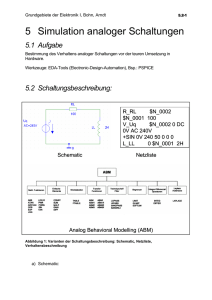
1 Lineare Netzwerke

Grundgebiete der Elektronik I, Bohn
1.1-1
1 Lineare Netzwerke
1
1.1 Schreibweise:
Häufig verwendete Vorsatzzeihen2:
G
M
k
c
m
µ
n
p
Giga
Mega
kilo
centi
milli
mikro
nano3
piko
109
106
103
10-2
10-3
10-6
10-9
10-12
Konventionen in der Elektrotechnik:
zeitlich konstante Größen: Großbuchstaben wie U, I , P, R
zeitliche variable Größen: Kleinbuchstaben wie u , i, p
(häufig, aber nicht immer, mit (t) gekennzeichnet, z.B. u(t) )
1 Literatur: Lehr und Übungsbuch Elektrotechnik, Altmann, Schlayer, Hanser Verlag,
Elektrotechnik für Ingenieure, Teil 1 und 2, Weißgerber, Vieweg Verlag,
Braunschweig
2
vorzugsweise werden die Vielfachen der 3-er Potenzen genommen
3
Altgriechisch: Zwerg!!
Grundgebiete der Elektronik I, Bohn
1.2-2
1.2 Grundbegriff des Stromkreises
1.2.1
Materialeigenschaften
Materialeigenschaften haben einen großen Einfluss auf die Ausbildung elektrischer
und magnetischer Felder und damit auf Ströme und Spannungen. Beim
Stromdurchgang durch einen Körper wird die Antriebsenergie der Ladungsträger
längs des Stromkreises vermindert. Der elektrische Widerstand eines Körpers ist ein
Maß dafür, wie sich der Körper dem Stromdurchgang widersetzt. Dies wird
wesentlich von den Materialeigenschaften bestimmt.
Wir unterscheiden folgende Kategorien des elektrischen Widerstands:
•
L e i t e r : Metalle, metallische Verbindungen (metallische Leitung) und
Elektrolyte (lonenleitung)
•
H a l b l e i t e r : Beispiel: Kohle, Silizium, Germanium, Selen etc.
•
N i c h t l e i t e r ( I s o l a t o r e n ) : Beispiel Glimmer, Quarz, Salze in fester
Form, Kunststoffe etc.
Die unterschiedliche Stromleitung fester Materialien wird durch das Bändermodell der
Atome beschrieben (siehe spätere Kapitel über Halbleiter). Es besagt, dass sich
Elektronen nur in bestimmten Energiebändern bewegen können. Für die
Stromleitung kommen nur das Valenzband mit den Valenzelektronen und das
Leitungsband mit den freien Elektronen in Frage. Bei Metallen überlappen sich diese
beiden Bänder, die Valenzelektronen können daher die Stromleitung übernehmen.
Bei Halbleitern sind Leitungsband und Valenzband energetisch nur sehr gering
getrennt. Bei Wärmezufuhr wandern Valenzelektronen in das Leitungsband und
stehen zur Stromleitung zur Verfügung. Bei Nichtleitern liegen Valenzband und
Leitungsband energetisch so weit auseinander, dass die Valenzelektronen die
vorhandenen wenigen freien Elektronen bei der Stromleitung nicht unterstützen
können.
Grundgebiete der Elektronik I, Bohn
1.2.2
Wirkungen des elektrischen Stroms
•
Wärmewirkung in einem Leiter
•
Stofftransport in Ionenleitern
•
Kraft im magnetischen Feld
(Prinzip aller elektrischen Maschinen)
1.2-3
Grundgebiete der Elektronik I, Bohn
1.3-4
1.3 Ersatzschaltbild des Stromkreises
Die Stromrichtung ist als Bewegungsrichtung der positiven Ladungsträger definiert.
(d.h. entgegengesetzt der Bewegungsrichtung der negativen Elektronen)
Vereinfachte Darstellung im:
1.3.1
Ersatzschaltbild mit idealer Spannungsquelle
Der Innenwiderstand R; berücksichtigt, dass die Quelle keinen beliebig großen Strom
liefern kann (z.B. Starterbatterie im Kurzschluss).
Grundgebiete der Elektronik I, Bohn
Alternative Darstellung im:
1.3.2
Ersatzschaltbild mit idealer Stromquelle
NB.: Die hier als 'Alternative' eingeführte Stromquelle hat bei etlichen realen
Bauelementen durchaus die primäre physikalische Bedeutung!
1.3-5
Grundgebiete der Elektronik I, Bohn
1.4-6
1.4 Der elektrische Widerstand
Die Stromstärke I (d.h. die Ladungsmenge pro Zeit durch einen Leiter) wird durch die
Stöße der Ladungsträger mit den Leiteratomen begrenzt. Durch Erhöhung der
Spannung wird normalerweise auch der Strom erhöht.
Hier gibt es den praktisch wichtigsten Fall:
Ohmsches Gesetz für konstanten Widerstand d.h. linearen Zusammenhang
zwischen U und I . Man spricht auch vom linearen Widerstand.
I ~U
I = G ⋅U
Leitwert G, Widerstand R
oder
1
⋅U
R
U
R=
I
U = R⋅I
I =
1.4.1.1
SI-EINHEITEN
[U ] V
= =Ω
[I ] A
[I ] A
[G ] =
= =S
[U ] V
[ R] =
Ohm
Siemens
Anmerkung: Nur der Idealfall eines Widerstands ist unabhängig von Strom und
Spannung. Reale Metallfilmwiderstände4 haben eine Temperaturabhängigkeit (bei
20°C typ. 0,015% Erhöhung pro K). Dioden zum Beispiel haben eine logarithmische
Strom-Spannungskennlinie.
Weitere Einflussgrößen, die Widerstände verändern können , sind:
1. Strahlung (Licht): Fotowiderstände (z.B. CdS)
2. Magnetfelder: Bi (Wismut), Feldplatten (Halbleiter)
•
•
4
zur Messung magnetischer Felder
für kontaktlose Schalter
Optimiert für geringe Temperaturabhängigkeit
Grundgebiete der Elektronik I, Bohn
1.4-7
3. Mechanische Dehnung: Dehnungsmessstreifen (DMS) (engl.: strain gauges)
(Dehnung einige Prozent -> ∆R ca. 1%)
1.4.2
Beispiele
An eine Batterie wird ein Verbraucher mit R = 7Ω angeschlossen. Die
Klemmenspannung beträgt 4V. Wie groß ist I?
Eine Autobatterie hat eine Leerlaufspannung von 14,2 V (2,37 V/Zelle) und gibt beim
Kurzschluss einen Strom von 1,2 kA ab. Wie groß ist der Innenwiderstand R;?
Grundgebiete der Elektronik I, Bohn
1.5-8
1.5 Energie und Leistung
1.5.1
Energie
Freigesetzte potentielle Energie einer Ladung Q beim Durchgang durch den
Widerstand R (dabei wird die Potentialdifferenz U durchlaufen).
Diese Energie wird in R in Wärme umgesetzt:
(1)
W = Q ⋅U
Außerdem ist I =
Q
bzw. Q = I ⋅ t
t
(2)
W =U ⋅ I ⋅t
Bei zeitveränderlichen Größen gilt:
τ2
W = ∫ u (t ) ⋅ i (t ) dt
(3)
τ1
Am Widerstand R gilt:
U = R⋅I
bzw. I =
U
R
damit gilt
(6)
(7)
oder für zeitveränderliche Größen u(t), i(t)
(8)
(9)
Grundgebiete der Elektronik I, Bohn
1.5.2
1.5-9
Leistung
P=
W
t
(Fall von konstanter Leistung)
mit (2)
P=
mit (6)
W U ⋅ I ⋅t
=
t
t
mit (7)
Beispiel:
Eine Halogenglühlampe hat eine Leistung von 50W bei
einer Versorgungsspannung von 12V. Wie hoch ist der
Strom?
Grundgebiete der Elektronik I, Bohn
1.5-10
2 Netzwerktheorie
Anwendung:
•
Berechnung der Ströme und Spannungen in komplizierten Schaltungen.
•
Bestimmung des Verhaltens der Schaltung vor dem Aufbau der Schaltung.
Vorbedingung: Die realen Bauelemente der Schaltung werden mit Hilfe von idealen
Bauelementen modelliert. Die realen Bauelemente werden nur näherungsweise
beschrieben. Erst durch diese Vereinfachung ist jedoch eine Berechnung möglich!5
Abbildung 2-1: PC-Netzteil, 5V, 12V, -5V, -12V
5
Will man Schweres bewältigen, muss man es sich leicht machen (Berthold Brecht).
Grundgebiete der Elektronik I, Bohn
2.1-11
2.1 Berechung von Netzwerken
2.1.1
Einfache Netzwerke
Aufstellen von Gleichungen
Auflösen nach den gesuchten Größen
2.1.2
Komplizierte Netzwerke (mit vielen Knoten)
systematisches Aufstellen von Gleichungssystemen durch
- Knotenspannungsanalyse oder
- Maschenstromanalyse
- Zweigstromanalyse
Auflösen der Gleichungssysteme
(verschiedene Verfahren in der Mathematik, z.B. direkte Auflösung durch Iteration)
Achtung:
Die Ergebnisse decken sich wegen der Idealisierung der Ersatzelemente und der
Umgebung nur näherungsweise mit der Wirklichkeit!
Vorläufig: Beschränkung auf Gleichstrom, später auch zeitabhängige Größen. Die
jetzt vorgestellten Gesetzmäßigkeiten gelten prinzipiell auch dort.
Grundgebiete der Elektronik I, Bohn
2.2-12
2.2 Ersatzschalbilder und Netzwerkelemente
Zweipol: (zwei Anschlüsse)
passive Zweipole
aktive Zweipole
passive
aktive
Vierpol: (vier Anschlüsse)
Begriffe
Grundgebiete der Elektronik I, Bohn
2.3-13
Ersatzelemente: sind idealisiert und beschreiben nur eine einzige Eigenschaft des
Stroms (hier: Widerstand, jedoch nicht elektrisches Feld (→ Kapazität) oder
magnetisches Feld (→ Induktivität)
'Leitungen': sind ohne jeden elektrischen Einfluss auf die Schaltung. Z.B. ein
ohmscher Leitungswiderstand müsste durch ein zusätzliches Ersatzelement RL
berücksichtigt werden.
2.3 Gesetze für die Berechnung von Strom- und
Spannungsverteilungen
2.3.1
Kirchhoffsche Knotenregel
(English: KCL, Kirchhoff's Current Law)
Begründung: die auf einen Knoten zufließende Ladung muss auch wieder abfließen
(Satz von der Erhaltung der Ladung bzw. Elektrizitätsmenge)
Man sagt:
Die Summe aller Einströmungen ist Null.
Grundgebiete der Elektronik I, Bohn
2.3.1.1
2.3-14
BEISPIEL
I1
I1=+1A
I2
I2=-3A
I3
I3=-3A
I4
I4=-2A
I5
I5=+4A
I6
Wie groß ist der Strom in dem nicht zugänglichen Leiter I6?
Lösung: Die Hüllflache über die gesamte Schaltung kann als ein Knoten aufgefasst
werden:
Grundgebiete der Elektronik I, Bohn
2.3.2
2.3-15
Kirchhoffsche Maschenregel
(engl.: KVL, Kirchhoffs Voltage Law)
Die Knotenpunkte 1,2,3,4,5
haben die Potentiale
ϕ1, ϕ2, ϕ3, ϕ4¸ϕ5
Für die Spannungen (Potentialdifferenz) gilt dann:
U 12 = ϕ 1 − ϕ 2
U 23 = ϕ 2 − ϕ 3
U 34 = ϕ 3 − ϕ 4
U 45 = ϕ 4 − ϕ 5
U 51 = ϕ 5 − ϕ 1
U 12 + U 23 + U 34 + U 45 + U 51 =
Allgemein: Allgemein: Wichtig: Die Zählpfeile der Zweigspannungen müssen überall
im gleichen Umlaufsinn gewählt werden.
Man sagt:
Die Umlaufspannung ist Null
Grundgebiete der Elektronik I, Bohn
2.3-16
2.3.3
Gleichungen der Netzwerkelemente
2.3.3.1
IDEAL OHMSCHER WIDERSTAND
(Darstellung hier im Verbraucher- Zählpfeilsystem VZS:
Strom- und Spannungspfeile in gleicher Richtung)
Ein idealer ohmscher Widerstrand ist ideal linear. Das Verhältnis von Spannung
zum Strom ist konstant.
2.3.3.2
REALE SPANNUNGSQUELLE UQ=const.
Leerlauf (kein Strom):
Kurzschluss:
(Darstellung hier im Erzeuger- Zählpfeilsystem EZS:
Strom- und Spannungspfeile in entgegen gesetzter Richtung)
Eine ideale Spannungsquelle liefert eine konstante Spannung unabhängig vom
Strom.
Grundgebiete der Elektronik I, Bohn
2.3.3.3
2.3-17
REALE STROMQUELLE IQ=const.
Leerlauf (kein Strom):
Kurzschluss:
Eine ideale Stromquelle liefert einen konstanten Strom unabhängig von der
Spannung.
2.3.3.4
BEISPIEL:
An einer Autobatterie (Starterbatterie)
wird eine Leerlaufspannung UL = 14,2V
und ein Kurzschlussstrom von IK = 4,5 kA
gemessen.
Geben Sie das Stromquellen- bzw. Spannungsquellenersatzschaltbild (ESB) an!
Spannungsquelle:
Grundgebiete der Elektronik I, Bohn
2.3-18
Stromquelle:
Beide Quellenarten können ineinander umgerechnet werden:
Spannungsquelle:
Ri
Stromquelle:
Iq
Ri
Uq
→ Man kann die jeweils besser geeignete Beschreibungsform wählen!
Grundgebiete der Elektronik I, Bohn
2.3.4
Einfache Netzberechnungen
2.3.4.1
REIHENSCHALTUNG VON WIDERSTÄNDEN
2.3-19
Maschengleichung:
Bei der Reihenschaltung von Widerständen addieren sich die Widerstandswerte.
Allgemein:
Grundgebiete der Elektronik I, Bohn
2.3.4.2
2.3-20
SPANNUNGSTEILER
Die Teilspannung verhält sich zur Gesamtspannung wie der Teilwiderstand zum
Gesamtwiderstand.
Teilspannung
Teilwiders tan d
=
Gesamtspannung Gesamtwiders tan d
Grundgebiete der Elektronik I, Bohn
Beispiel: Bestimmen Sie die Ausgangsspannungen dieser Schaltung:
900Ω
U e = 12V
90Ω
10Ω
U a1
U a2
2.3-21
Grundgebiete der Elektronik I, Bohn
2.3.5
Parallelschaltungen
Knotengleichungen:
Bei der Parallelschaltung von Widerständen addieren sich die Leitwerte.
RG =
1
1
1
1
+
+ +... +
R1 R2
Rn
2.3-22
Grundgebiete der Elektronik I, Bohn
2.3.5.1
SPEZIALFALL: 2 PARALLEL GESCHALTETE
WIDERSTÄNDE R1 UND R2:
2.3.5.2
STROMTEILER
Der Teilstrom verhält sich zum Gesamtstrom wie der gegenüberliegende
Widerstand zur Summe der Widerstände.
2.3-23
Grundgebiete der Elektronik I, Bohn
Beispiel:
2.3-24
Grundgebiete der Elektronik I, Bohn
2.3-25
Grundgebiete der Elektronik I, Bohn
2.4-26
2.4 Netzwerkumwandlungen
Netzwerke lassen sich häufig vereinfachen, in dem Elemente zusammengefasst oder
umgewandelt werden.
2.4.1
Reihenschaltungen
Beispiel: Reihenschaltungen zweier Batterien:
Grundgebiete der Elektronik I, Bohn
2.4.2
Beispiel:
Parallelschaltungen
2.4-27
Grundgebiete der Elektronik I, Bohn
Achtung:
• Ideale Stromquellen können nicht in Reihe geschaltet werden
•
Ideale Spannungsquellen können nicht parallel geschaltet werden
•
Parallelschaltung von Spannungs- und Stromquelle entspricht
Spannungsquelle
2.4-28
Grundgebiete der Elektronik I, Bohn
•
Reihenschaltung von Spannungs- und Stromquelle
N.B.: Man kann sich das leicht merken, in dem man den Kringel um das
Quellensymbol sich wegdenkt:
2.4-29
Grundgebiete der Elektronik I, Bohn
2.4.3
2.4-30
Ersatzquellen
Netzwerk mit konstanten Quellen und linearen, passiven Elementen.
Die Verhältnisse lassen sich vollständig durch eine Ersatzquelle beschreiben:
Ersatzspannungsquelle
Ersatzstromquelle
(English: Thevenin's Theorem)
(English: Norton's Theorem)
Bestimmung der Kenngrößen durch Rechnung oder Messung am ursprünglichen
Netzwerk:
• Leerlauf: U = UL = Uq
• Kurzschluss: I = IK= Iq
U
• Ersatz- Innenwiderstand: Ri = L
IK
N.B.: Der Innenwiderstand lässt sich auch durch Widerstandsmessung zwischen den
Klemmen bestimmen (bzw. berechnen).
Dazu:
• Stromquellen: offene Verbindung (da Ri = ∞ ).
•
Spannungsquellen kurzgeschlossen (da Ri = 0 ).
Grundgebiete der Elektronik I, Bohn
Beispiel: belasteter Spannungsteiler
Bestimmen Sie die Ersatzspannungsquelle.
Wie groß muss RL mindestens sein, dass sich U2 um höchstens n % ändert?
2.4-31
Grundgebiete der Elektronik I, Bohn
2.4-32
Die Bestimmung von Strom und / oder Spannung über Ersatzquellen ist besonders
gut geeignet, wenn bei einem Netzwerk nur ein Zweig interessiert. Je nach Netzwerk
kann das z.B. das Verhalten an den Klemmen identisch sein, aber im Inneren sehr
unterschiedlich.
2.4.4
Gesteuerte Quellen
Es gibt vier Typen von gesteuerten Quellen:
Spannungsquelle
spannungsgesteuert
stromgesteuert
Stromquelle
spannungsgesteuert stromgesteuert
Feldeffekttransistor6 Bipolartransistor
(FET)
Bsp.: Vakuumtriode
Spannungsverstärker
Spannungsverstärkung7
Steilheit
Stromverstärkung
N. B.: gesteuerte Quellen werden vorteilhaft zur Beschreibung aktiver Bauelemente
(Transistoren, ICs, Röhren etc.) eingesetzt.
Beispiel: Transistor mit Stromverstärkung 100, Basis-Emitterspannung ca. 0,7V
Bauteil:
Schaltzeichen:
vereinfachtes Modell:
6
Erstes Patent: Oskar Ernst Heil, 1934
7
Beispiel: TDA 7056, 3W-Verstärker für Ton von Fernsehgeräten, v = 100.
Grundgebiete der Elektronik I, Bohn
2.4.5
2.4-33
Leistungsanpassung
Betrachtung am Beispiel einer Spannungsquelle. Die Betrachtung einer Stromquelle
käme zum selben Ergebnis
damit ergibt sich die Leistung am Verbraucher (Nutzleistung)
und die Leistung am Innenwiderstand (Verlustleistung)
Die Leistung der Quelle (Quellenleistung) ergibt sich zu
Grundgebiete der Elektronik I, Bohn
2.4-34
Hieraus ergeben sich verschieden Fragestellungen hinsichtlich einer Optimierung
von Leistungen (bei gegebenem U, und R;):
1. Maximal mögliche Verbraucherleistung PV
wichtig in der Nachrichtentechnik zur Erzielung eines möglichst großen Signals
2. Maximal möglicher Wirkungsgrad η =
PV
Pq
wichtig in der Energietechnik zur Energieerzeugung und -verteilung mit
möglichst kleinen Verlusten
2.4.5.1
MAXIMAL MÖGLICHE VERBRAUCHERLEISTUNG
Ansatz: PV hat ein Maximum (oder Minimum) bei
dPv
=0
dRv
Ergebnis: Ri = Rv
Für die maximale Verbraucherleistung muss der Generatorinnenwiderstand Ri
gleich dem Verbraucherwiderstand Rv sein.
dann ist PV , max =
2.4.5.2
U q2
4 ⋅ Ri
.
MAXIMAL MÖGLICHER WIRKUNGSGRAD
Rv
P
Rv
Ri
η= v =
=
R
Pq Ri + Rv
1+ v
Ri
Für optimalen Wirkungsgrad η muss der Generatorinnenwiderstand Ri im
Verhältnis zu Rv möglichst klein gehalten werden.
Grundgebiete der Elektronik I, Bohn
2.4-35
Ausnutzungsdiagramm
1,0
0,75
0,5
0,25
Unteranpassung
1
Rv< Ri
Kurzschluss
Rv=0
Überanpassung
Rv> Ri
Anpassung
Rv= Ri
Rv
Ri
Grundgebiete der Elektronik I, Bohn
2.4-36
Beispiel
Gegeben: 2 Akkuzellen (U, = 2 V, R; = 50mΩ), 2 Verbraucherwiderstände Rv = 0,2Ω
1. Wie ist die Schaltung für maximale Leistung PV?
2. Wie ist die Schaltung für besten Wirkungsgrad η?
Grundgebiete der Elektronik I, Bohn
2.4-37
3 Systematische Analyse linearer
Netzwerke
Grundgebiete der Elektronik I, Bohn
3.1-38
3.1 Knotenspannungsverfahren
Vorbedingung: Netzwerk aus Widerständen und STROMQUELLEN
•
Festlegung eines Bezugsknotens (hier 4 ) → U 4 ≡ 0
•
Zählpfeilrichtung der übrigen Knoten: zum Bezugsknoten hin.
•
Quellen als Stromquellen. Die Ströme werden als Belastungsströme gezählt. die
U = 0 sind in allen Maschen automatisch
Kirchhoffschen Maschengleichungen
(∑
)
erfüllt.
z. B. Masche 1-2-4-1: U 12 + U 24 + U 41 = 0, d.h. (U 1 − U 2 ) + U 2 − U 1 = 0,
•
Aufstellen der Netzwerkgleichungen mit Hilfe der Kirchhoffschen Knotenregel
(∑ I = 0) .
Knoten 1, Knotenregel:
Y11=GA+GD+GE
Umlaufadmittanz des Knotens 1
Y12=GA
Koppeladmittanz zwischen Knoten 1 und Knoten 2
Y13=GD
Koppeladmittanz zwischen Knoten 1 und Knoten 3
Grundgebiete der Elektronik I, Bohn
3.1-39
Gleichungen für alle Knoten direkt ablesen:
Iq3
Iq1
Iq2
‫ܫ‬௤ଵ
−(‫ܩ‬஺ + ‫ܩ‬஽ + ‫ܩ‬ா )
‫ܩ‬஺
‫ܩ‬஽
ܷଵ
‫ܩ‬஺
−(‫ܩ‬஺ + ‫ܩ‬஻ + ‫ܩ‬ி )
‫ܩ‬ி
ቌ
ቍ × ൭ܷଶ ൱ = ቌ‫ܫ‬௤ଶ ቍ
ܷଷ
‫ܩ‬஽
‫ܩ‬ி
−(‫ܩ‬஽ + ‫ܩ‬ி + ‫ܩ‬஼ )
‫ܫ‬௤ଷ
Umlaufadmittanz
Koppeladmittanz
Knotenspannungen (bezogen auf Bezugsknoten)
Stromquellen (betrachtet als Belastungsstrom, + Strom aus dem Knoten)
−ܻଵଵ
൭ ܻଵଶ
ܻଵଷ
ܻଵଶ
−ܻଶଶ
ܻଶଷ
Y
‫ܫ‬௤ଵ
ܻଵଷ
ܷଵ
ܻଶଷ ൱ × ൭ܷଶ ൱ = ቌ‫ܫ‬௤ଶ ቍ
ܷଷ
−ܻଷଷ
‫ܫ‬௤ଷ
Y Matrix der Knotenadmittanzen
U Vektor der Knotenspannungen
Iq Vektor der Stromquellen
x U
= Iq
Grundgebiete der Elektronik I, Bohn
3.1-40
Vorteile des Knotenspannungsverfahrens:
•
Anzahl der Gleichungen ist sofort klar: n = k − 1
wobei k Zahl der Knoten, n Zahl der Gleichungen.
•
Es müssen keine Maschen (o. ä.) definiert werden
•
Knotenadmittanzmatrix kann einfach aufgestellt werden und besitzt meist viele
Nullelemente.
→ als SW realisierbar
•
Verfahren ist Basis für Netzwerkanalyse durch Computer!
Allgemeine Hinweise zu Netzwerkberechnungen:
•
Stromquellen sind keine Zweige
•
Ein Knoten sind alle verbundenen Punkte eines Netzwerks mit gleichem
Potential
•
Zwei hintereinander geschaltete Zweige ohne weitere Elemente, die am
Verbindungsknoten angeschlossen sind, können zu einem Zweig
zusammengefasst werden:
Grundgebiete der Elektronik I, Bohn
3.2 Netzwerkumwandlungen
3.2.1
Vereinfachungen
Siehe Kapitel 2.4.
3.2.2
Behandlung von Spannungsquellen
1. Einzelne Spannungsquelle mit (Innen-)Widerstand als Zweig
Umwandeln in Stromquelle
3.2-41
Grundgebiete der Elektronik I, Bohn
3.2-42
2. Zweig nur mit Spannungsquelle (ohne Widerstand)
Spannungsquelle verschieben und anschließend in Stromquellen umwandeln
Grundgebiete der Elektronik I, Bohn
3.3-43
3.3 Auflösung nach den Knotenspannungen
Lösungswege:
a) Matrixinversion:
b) Cramersche Regel:
 − Y11

Beispiel: Gleichungssystem:  Y12
 Y
 13
-> U 1 =
 I q1

det  I q 2
I
 q3
 − Y11

det  Y12
 Y
 13
Y12
− Y22
Y23
Y13 

Y23 
− Y33 
Y12
− Y22
Y23
Y13 

Y23 
− Y33 
Y12
− Y22
Y23
, U2 =
Y13   U 1   I q1 
    
Y23  ⋅ U 2  =  I q 2 
− Y33   U 3   I q 3 
 − Y11

det  Y12
 Y
 13
 − Y11

det  Y12
 Y
 13
c) Gaußscher Algorithmus
Überführen des Gleichungssystems in die Form
 B11

 0
 0

B12
B22
0
B13   U1   V1 
    
B23  ⋅ U 2  = V2 
C33  U 3   V3 
damit ergibt sich:
U3 =
V3
C 33
U2 =
V 2 − B23 ⋅ V3
B22
U1 =
V1 − B12 ⋅ V2 − B13 ⋅ V3
B11
I q1
I q2
I q3
Y12
− Y22
Y23
Y13 

Y23 
− Y33 
Y13 

Y23 
− Y33 
, ...
Grundgebiete der Elektronik I, Bohn
3.3-44
d) Iteration:
Start mit geschätzten Strömen, z.B. U1 = 1 V, U2 = 1V, U3 = 1V (so genannter
Startvektor)
→ verbesserte Werte für U1, U2, U3 berechnen8:
U1 =
1
(Y12 ⋅ U 2 + Y13 ⋅ U 3 − I q1 )
Y11
U2 =
1
(Y12 ⋅ U 1 + Y23 ⋅ U 3 − I q 2 )
Y22
U3 =
1
(Y13 ⋅ U 1 + Y23 ⋅ U 2 − I q3 )
Y33
Vergleich der neuen Werte mit den vorhergehenden Werten
Differenz ausreichend klein ?
nein: Schleife erneut durchlaufen ja: Abbruch
8
Z. B. aus 1. Zeile des Gleichungssystems:
− Y11 ⋅ U 1 + Y12 ⋅ U 2 + Y13 ⋅ U 3 = I q1
⇒
U1 =
1
(Y12 ⋅U 2 + Y13 ⋅U 3 − I q1 )
Y11
⇒
Y12 ⋅ U 2 + Y13 ⋅ U 3 − I q1 = Y11 ⋅ U 1
Grundgebiete der Elektronik I, Bohn
3.3.1
Beispiele:
Beispiel 1
mit Ri=Rv=R1=R2=R3=R
Gesucht: UE, UA
3.3-45
Grundgebiete der Elektronik I, Bohn
3.3-46
Grundgebiete der Elektronik I, Bohn
Beispiel 2
3.3-47
Grundgebiete der Elektronik I, Bohn
4 Grundbegriffe der
Wechselstromtechnik
Typische Anwendungsgebiete:
• Elektroenergieversorgung
• Antriebstechnik
• Elektroakustik. Bsp.: Berechnung von Frequenzgängen
(Wie verhält sich ein Verstärker bei 10Hz, 100Hz, 20000 Hz)
• Nachrichtechnik
4.1 Sinusförmige Wechselgrößen
Nichtsinusförmige, aber periodische Wechselgröße:
Wechselgrößen:
•
eingeschwungener Zustand (keine Ein- oder Ausschaltvorgänge)
•
Wiederkehr des gleichen Amplitudenwertes nach der Periodendauer T
f (t + T ) = f (t )
•
beliebiger Zeitverlauf
•
Mittelwert ist gleich Null.
4.1-48
Grundgebiete der Elektronik I, Bohn
4.1-49
Beispiele:
t
t
t
t
Nachfolgend werden die sinusförmigen Wechselgrößen wegen ihrer überragenden
technischen Bedeutung behandelt.
Beispiel: Erzeugung von Wechselspannung in einem Generator
Abbildung 4-1: Prinzip des Wechselstromgenerators, Generator in Wasserkraftwerk
Bei konstanter Drehzahl ergibt sich eine induzierte Quellenspannung. Die Ursache
dafür ist der zeitlich veränderliche magnetische Fluss.
Magnetischer Fluss durch den Rotor:
φ (t ) = φˆ ⋅ sin( 2 ⋅ π ⋅ f ⋅ t )
wobei φˆ maximaler Fluss, f Frequenz der Drehung,
t Zeit
Grundgebiete der Elektronik I, Bohn
4.1-50
Die Änderung des Flusses erfolgt durch Drehung des Rotors.
Induktion einer Spannung (Induktionsgesetz9)
dφ
wobei N Windungszahl
u (t ) = N ⋅
dt
d.h.
d
u (t ) = N ⋅ φˆ ⋅ sin( 2 ⋅ π ⋅ f ⋅ t )
dt
= N ⋅ φˆ ⋅ 2 ⋅ π ⋅ f ⋅ cos( 2 ⋅ π ⋅ f ⋅ t )
(
)
= N ⋅ φˆ ⋅ ω ⋅
cos(ω ⋅ t )
=
uˆq ⋅
cos(ω ⋅ t )
=
uˆq ⋅
π

sin  ω ⋅ t + 
2

wobei ω = 2 ⋅ π ⋅ f
û q Scheitelwert
Kreisfrequenz,
f (t )
|
0
0°
9
|
|
|
0,5π
90°
|
|
π
|
|
|
|
1,5π
180°
270°
|
Das Induktionsgesetz wird in der Physikvorlesung ausführlicher behandelt.
|
|
2π
360°
|
ω ⋅t
Grundgebiete der Elektronik I, Bohn
4.1-51
Phasenlage
Beispiel:
f (t )
|
− 0 ,33π
− 60 °
|
|
0
|
0 ° + 30 °
u (t ) = uˆ ⋅ sin(ωt + 60°)
= uˆ ⋅ sin(ωt + ϕU )
|
|
0 ,5π
90 °
|
|
π
|
|
1,5π
180 °
270 °
|
ˆ ⋅ sin(ωt − 30°)
φ (t ) = Φ
ˆ ⋅ sin(ωt + ϕ )
=Φ
φ
Die Spannung u eilt dem Fluss φ um 90° voraus:
ϕ U − ϕ φ = +90°
Der Fluss φ eilt der Spannung u um 90° nach:
ϕ φ − ϕ U = +90°
|
|
|
|
2π
360°
|
ω ⋅t
Grundgebiete der Elektronik I, Bohn
4.1-52
Beispiel: Ablesen vom Oszilloskop
40
30
20
V
10
0
-10
-20
-30
-40
-5
0
5
10
s
15
20
-3
x 10
Grundgebiete der Elektronik I, Bohn
4.2-53
4.2 Kennwerte
4.2.1
Periodendauer und Frequenz
Für die sinusförmige Wechselspannung gilt:
u (t ) = uˆ ⋅ sin(ωt + ϕ )
Der Augenblickswert wiederholt sich nach Ablauf
des Winkels
mit t = T: Periodendauer
360° = 2π = ωT
1
= f : Anzahl der Perioden pro Zeiteinheit: Frequenz
T
[ f ] = 1 = Hz
s
4.2.1.1
(Hertz)
TECHNISCH WICHTIGE FREQUENZEN
16 2/3 Hz
Bahnstromversorgung (Deutschland und Mitteleuropa)
50 Hz und 60 Hz
Elektroenergieversorgung
300 Hz bis 3,4 kHz
Sprachübertragung (Telefonkanal)
16 Hz bis 20 kHz
Elektroakustik (HiFi)
100 kHz bis 10 GHz
Nachrichtentechnik
einige 100 THz optische
Nachrichtentechnik
noch höhere Frequenzen werden meist mit ihrer Wellenlänge angegeben, z. B. bei:
Mikrowellen
Infrarotlicht
sichtbares Licht
ultraviolettes Licht
Röntgenstrahlen
y-Strahlen
Grundgebiete der Elektronik I, Bohn
4.2.1.2
KREISFREQUENZ
ω = 2 ⋅π ⋅ f
4.2.2
4.2-54
wobei [ω ] =
1
s
Scheitelwert
Kennzeichnet die höchste Amplitude:
Bedeutung:
Spannung: elektrische Feldstärke: höchste elektrische Beanspruchung (Bemessung
der Isolation)
Strom: magnetische Feldstärke: höchste mechanische Beanspruchung
(mechanische Auslegung von Leitern)
Messung:
Digitaloszilloskop
Messschaltung für Scheitelwerte (Spitzenwert-Messgerät)
Grundgebiete der Elektronik I, Bohn
4.2.3
4.2-55
Effektivwert
Bedeutung: Wärmewirkung des elektrischen Stroms (Beispiel 50W Glühlampe)
Ein Wechselstrom mit Effektivwert 1A hat die
gleiche Wärmewirkung an einem Widerstand
wie ein Gleichstrom mit Wert 1A.
Berechnung:
Gleichstrom:
P = R⋅I2
Wechselstrom:
P=
1
T
T
∫ p(t )dt =
0
T
T
1
1
R ⋅ i 2 (t ) dt =R ⋅ ∫ i 2 (t ) dt
∫
T 0
T 0
T
1 2
i (t )dt
T ∫0
-> I =
Bei i (t ) = iˆ ⋅ sin( ω t ) (Wechselstrom) ergibt sich
I=
iˆ
2
Der Effektivwert von sinusförmigem Wechselstrom / spannung ist um den Faktor
kleiner als sein Scheitelwert.
Beispiel Netzspannung:
2
Grundgebiete der Elektronik I, Bohn
4.2-56
4.2.4
Beschreibung sinusförmiger Wechselgrößen durch
Kennwerte
x (t ) = xˆ ⋅ sin( ωt + ϕ )
Grundgebiete der Elektronik I, Bohn
4.3-57
4.3 Komplexe Rechnung, Zeigerdiagramme
Darstellung von Sinusfunktionen und Rechnung mit Sinusfunktionen ist aufwendig
und nicht sehr anschaulich.
4.3.1.1
BEISPIEL: ADDITION ZWEIER SPANNUNGEN IM
ZEITBEREICH
Grundgebiete der Elektronik I, Bohn
4.3.2
4.3-58
Zeigerdarstellung
Alternative: neue Darstellungsform, d.h. die die Addition und andere
Zusammenhänge auf geometrische Weise grafisch sehr anschaulich macht:
Zeigerdarstellung:
Beispiel: Netzfrequenz 50Hz, T=1/f=1/50Hz=
t=0
t=2,5ms
t=5ms
Die Funktion u (t ) = uˆ ⋅ sin( ω t ) Iässt sich durch einen umlaufenden Zeiger darstellen:
Zeigerlänge: û ⋅
Umlaufwinkelgeschwindigkeit ω
Der zu einem Zeitpunkt t (bzw. einem Winkel ωt) gehörende Momentanwert u(t)
ergibt sich
aus der Projektion des Zeigers auf die u-Achse
Phasenverschiebungen werden durch ein Verdrehen des Zeigers um den Winkel ϕ
berücksichtigt.
Grundgebiete
undgebiete der Elektronik I, Bohn
4.3-59
Die Addition von Wechselgrößen gleicher Frequenz erfolgt durch geometrische
Addition der Zeiger.
Die Addition der Zeiger erfolgt zum Zeitpunkt t = 0.
0
U g = U1 +U 2
statt
u1 (t ) + u 2 (t ) = uˆ1 sin(ωt + ϕ1 ) + uˆ 2 sin(ωt + ϕ 2 )
u (t ) = uˆ g sin(ωt + ϕ g )
Die geometrische Addition ist wesentlich einfacher und anschaulicher als die
arithmetische Berechnung. Man muss jedoch eine mathematische Form der
Beschreibung der Zeiger
Zeiger finden. Hierfür eignet sich besonders die komplexe
Rechnung
Rechnung.
Grundgebiete der Elektronik I, Bohn
4.3.3
4.3-60
Zeiger in der komplexen Ebene
Beschreibung der Ebene durch x, y- Koordinaten oder durch Angabe einer reellen
Zahl x und einer imaginären Zahl j ⋅ y mit j als imaginäre Einheit j = − 1 .
Die komplexe (zusammengesetzte) Zahl
z = x+ j⋅ y
beschreibt einen Punkt in der komplexen Ebene und einen vom Nullpunkt
ausgehenden Zeiger.
In der X – y-Ebene wird der zur Funktion
u (t ) = uˆ ⋅ sin( ω t )
gehörende Kreis durch:
x = uˆ ⋅ cos(ωt )
y = uˆ ⋅ sin(ωt )
beschrieben.
x 2 + y 2 = û 2
ist eine Kreisgleichung in Parameterform.
In komplexer Schreibweise lautet dies:
u = uˆ cos(ωt ) + j ⋅ uˆ ⋅ sin(ωt )
Nach der Euler-Gleichung gilt:
u = uˆ ⋅ e jωt
Grundgebiete der Elektronik I, Bohn
Positiver Winkel: gegen den Uhrzeigersinn
Negativer Winkel: mit dem Uhrzeigersinn
4.3.4
Rechenregeln für komplexe Größen
4.3.4.1
BILDUNG DER KONJUGIERT KOMPLEXEN ZAHL:
*
z = ( x + jy) * = x − jy
*
(
z = r ⋅ e jα
)
*
= r ⋅ e − jα
d.h. z wird an der reellen Achse gespiegelt.
4.3.4.2
BILDUNG DES BETRAGS UND DES WINKELS:
z = r ⋅ e jα = r
∠(z ) = α
Der Betrag einer komplexen Zahl ist die Zeigerlänge.
Oder
z = x + jy =


α =


x2 + y2
y
x
y
arctan + π
x
arctan
wenn x ≥ 0
wenn x < 0
4.3-61
Grundgebiete der Elektronik I, Bohn
4.3.4.3
4.3-62
WICHTIGE SPEZIALFÄLLE:
e j 0° = e j 0 = 1
e j 90° = e jπ / 2 = j
e j180° = e jπ = −1
e j 270° = e j 3π / 2 = − j
ebenso
4.3.4.4
e j ( −90°) = e − jπ / 2 = − j
ADDITION UND SUBTRAKTION:
z1 + z 2 = ( x1 + jy1 ) + ( x2 + jy2 ) = ( x1 + x2 ) + j ( y1 + y2 )
z1 − z 2 = ( x1 + jy1 ) − ( x2 + jy2 ) = ( x1 − x2 ) + j ( y1 − y2 )
Die Addition erfolgt durch getrennte Addition von Real- und Imaginärteilen.
4.3.4.5
MULTIPLIKATION UND DIVISION
z1 ⋅ z 2 = r1 ⋅ e jα 1 ⋅ r2 ⋅ e jα 2 = r1 ⋅ r2 ⋅ e j (α 1+α 2 )
d.h.
Multi
plikat
ion
der
Beträ
ge und Addition der Winkel
Bsp.:
z1 r1 ⋅ e jα 1 r1 j (α 1−α 2 )
=
= ⋅e
z 2 r2 ⋅ e jα 2 r2
d.h. Division der Beträge und Subtraktion der Winkel
Bsp.:
Grundgebiete der Elektronik I, Bohn
4.3-63
Grundgebiete der Elektronik I, Bohn
4.3-64
Spezialfall:
z ⋅ z = r ⋅ e jα ⋅ r ⋅ e − jα = r 2 ⋅ e j ( 0 ) = r 2
*
Der Betrag einer komplexen Zahl wird bestimmt durch Multiplikation mit der komplex
konjugierten Zahl und Wurzelbildung.
Bsp.:
4.3.4.6
n
POTENZIEREN UND RADIZIEREN:
(
z = r ⋅ e jα
n
)
n
= r n ⋅ e jα ⋅ n
z = n r ⋅ e jα = n r ⋅ e jα / n
Achtung: das Wurzelziehen ist mehrdeutig wegen der Periodizität der Drehung
4.3.4.7
DIFFERENZIEREN UND POTENZIEREN:
Dies ist von besonderer Bedeutung für die Differentialgleichungen in der
Elektrotechnik:
Behandlung im Zeitbereich
Behandlung im Komplexen
u (t ) = uˆ ⋅ sin( ω t + ϕ )
u = uˆ ⋅ e ( jωt +ϕ ) = uˆ ⋅ e jϕ ⋅ e jωt
du
= uˆ ⋅ ω ⋅ cos(ωt + ϕ )
dt
du
= uˆ ⋅ e jϕ ⋅ jω ⋅ e jωt = jω ⋅ u
dt
d 2u
= uˆ ⋅ − ω 2 ⋅ sin(ωt + ϕ )
dt 2
)
d 2u
2
2
= uˆ ⋅ e jϕ ⋅ ( jω ) ⋅ e jωt = ( jω ) ⋅ u
dt 2
cos(ωt + ϕ )
∫u
(
−1
∫ u dt = uˆ ⋅ ω
dt = uˆ ⋅ e jϕ ⋅
1
1
⋅ e jω t =
⋅u
jω
jω
Differenzieren und integrieren bedeutet im Komplexen lediglich Multiplikation mit jω
1
und
jω
.
Es tritt immer die gleiche Zeitabhängigkeit als Faktor e jωt auf. Er kann deshalb aus
allen Gleichungen heraus gekürzt werden. Man kann auch sagen, alle Vorgänge
werden nur für den
Zeitpunkt t = 0 betrachtet: e jωt →
= 1.
Grundgebiete der Elektronik I, Bohn
4.3.5
Begriffe für das Rechnen mit komplexen Größen
u , u (t )
Zeitfunktion
û
Amplitude, Spitzenwert
U
Effektivwert
u
komplexe Zeitfunktion
û
komplexe Amplitude
U
4.3-65
komplexer Effektivwert
u (t ) = uˆ ⋅ sin( ω t + ϕ )
U=
1
u (t ) = 300V ⋅ sin( 314 t + 40 °)
s
û
2
u = uˆ ⋅ e jϕ ⋅ e jωt
u = uˆ ⋅ e jωt
uˆ = uˆ ⋅ e jϕ
uˆ
U =
2
U = U ⋅ e jϕ
Bsp. f=50Hz -> ω = 2π ⋅ f = 314
1
s
Beim Rechnen mit komplexen Amplituden oder komplexen Effektivwerten stellt man
sich vor, dass die mit der Kreisfrequenz rotierenden Zeiger zum Zeitpunkt t = 0
'eingefroren' sind. Die Phasenwinkel ϕ1 und ϕ2 kennzeichnen die relative Lage der
Zeiger U 1 und U 2 , die auch bei Rotation um ωt unverändert erhalten bleibt.
Grundgebiete der Elektronik I, Bohn
4.4 Schaltungselemente in Wechselstromkreisen
4.4.1
Der (Wirk-) Widerstand
u = R ⋅i
u = uˆ ⋅ sin ωt
u uˆ
= ⋅ sin ωt = iˆ ⋅ sin ωt
R R
uˆ
iˆ =
R
1
komplex: I = ⋅ U
R
i=
u und i sind gleichphasig, d.h. die Phasenverschiebung ist Null.
4.4-66
Grundgebiete der Elektronik I, Bohn
4.4.2
Induktivität / Spule
di
dt
Bei Wechselstrom:
u = L⋅
i = iˆ ⋅ sin ωt
damit:
π

u = L ⋅ iˆ ⋅ ω ⋅ cos ωt = ωL ⋅ iˆ ⋅ sin ωt + 
2

π

= uˆ ⋅ sin ωt + 
2

Es gilt:
uˆ = ωL ⋅ iˆ
Die Spannung eilt dem Strom um 90° voraus.
komplex:
U = jωL ⋅ I
4.4-67
Grundgebiete der Elektronik I, Bohn
4.4.3
Kapazität / Kondensator
1
⋅ i (t ) dt
C ∫
Bei Wechselstrom:
u=
i = iˆ ⋅ sin ωt
damit:
−1
1 ˆ
π

u = iˆ ⋅
⋅ cos ωt =
⋅ i ⋅ sin ωt − 
2
ω ⋅C
ωC

π

= uˆ ⋅ sin  ωt − 
2

Es gilt:
uˆ =
1 ˆ
⋅i
ωC
Die Spannung hinkt dem Strom um 90° nach.
komplex:
U =
1
⋅I
jω C
4.4-68
Grundgebiete
undgebiete der Elektronik I, Bohn
4.5-69
4.5 Leistung und Energie
4.5.1
Beschreibung im Zeitbereich
4.5.1.1
WIRKLEISTUNG
Momentanwert der Leistung: s (t ) = u (t ) ⋅ i (t ) = R ⋅ i 2 (t ) =
u 2 (t)
R
Dauernde aber pulsierende Energiezufuhr (Wärmeentwicklung)
Mittlere Leistung, Wirkleistung:
T
S=P=
T
1
1
u ⋅ idt = R ⋅ ⋅ ∫ i 2 dt
∫
T 0
T 0
P = R⋅I2 =
U2
1 uˆ 2 1 ˆ
1
= U ⋅ I = R ⋅ iˆ 2 =
= uˆ ⋅ i
R
2 R 2
2
Einheit [P] = W = V ⋅ A
(siehe Tabelle in Kap. 4.3.5)
Grundgebiete der Elektronik I, Bohn
4.5.1.2
4.5-70
INDUKTIVE BLINDLEISTUNG
s (t ) = u (t ) ⋅ i (t ) = L ⋅
di
⋅ i = L ⋅ iˆ ⋅ ω ⋅ cos ωt ⋅ iˆ ⋅ sin ωt = ωL ⋅ iˆ 2 ⋅ 12 ⋅ sin (2ωt ) = uˆ ⋅ iˆ ⋅ sin (2ωt )
dt
pulsierende Energieaufnahme und Energieabgabe jeweils eine Viertelperiode lang
(t = T4 ,
ωT = π4 ) . Das Magnetfeld wird abwechseln auf- und wieder abgebaut. Es
erfolgt keine dauernde Energiezufuhr, das heißt P = S = 0 . Allerdings wird 'Energie
bewegt', man spricht deshalb von induktiver Blindleistung
Energieaufnahme in einer Viertelperiode:
T /4
Wmag =
∫ u (t ) ⋅ i(t )dt =
0
T /4
1
2
0
∫
⋅ ωL ⋅ iˆ 2 ⋅ sin (2ωt )dt = 12 ωL ⋅ iˆ 2 (−
T
1
2ω
⋅ cos(2ωt )) 4 = 14 L ⋅ iˆ 2 (1 + 1) = 12 ⋅ L ⋅ iˆ 2
0
Grundgebiete
undgebiete der Elektronik I, Bohn
Definition der induktiven Blindleistung
Q = + 12 ⋅ uˆiˆ = + 12 ⋅ ωL ⋅ iˆ 2 = + 12 X L ⋅ iˆ 2
Q = +U ⋅ I = +ωL ⋅ I 2
= +XL ⋅ I2
Q ist eine Rechengröße, keine physikalische Leistung!
[Q] = Var
Var: VoltVolt AmpereAmpere reaktiv
N.B.: Watt ist für die Wirkleistung reserviert!
4.5.1.3
KAPAZITIVE BLINDLEISTUNG
s(t ) = u (t ) ⋅ i (t ) =
1
ωC
⋅
( ∫ idt )⋅ i =
1
C
1
C
⋅ (− ω1 ) ⋅ iˆ ⋅ cosωt ⋅ sin ωt = ω−C1 ⋅ iˆ 2 ⋅ 12 ⋅ sin(2ωt ) =
iˆ 2
sin(2ωt + π ) = 12 ⋅ uˆ ⋅ iˆ ⋅ sin(2ωt + π )
2
pulsierende Energieaufnahme und Energieabgabe (Ladung und Entladung der
Kapazität)
Kapazität).
P=S =0
4.5-71
Grundgebiete der Elektronik I, Bohn
Energieaufnahme in einer Viertelperiode:
T
2
Wkap = ∫ − 12 ω1C ⋅ iˆ 2 sin (2ωt )dt
T
4
T
2
−1 ˆ2 1
=
⋅ i (− ωC ⋅ cos(2ωt ))
2ωC
T
4
= 14 ωC ⋅ uˆ 2 ω1 (cos ωT − cos ω2T )
= 12 ⋅ C ⋅ uˆ 2
1
2
⋅ C ⋅ û 2 : kapazitiv gespeicherte Energie am Kondensator für u (t ) = uˆ .
Definition der kapazitiven Blindleistung
Q = − 12 ⋅ uˆiˆ = − 12 ⋅ ω1C ⋅ iˆ 2 = − 12 X C ⋅ iˆ 2 = − 12 BC ⋅ uˆ 2
Q = −U ⋅ I = − ω1C ⋅ I 2
4.5.1.4
= −XC ⋅ I 2
= − BC ⋅ U 2
BEISPIEL:
Leerlaufendes Kabel mit C = 3 µF
Spannungsprüfung mit U = 6 kV und F = 50 Hz
Frage: Blindleistung = ?, Ladestrom = ?
4.5-72
Grundgebiete der Elektronik I, Bohn
4.6-73
4.6 Berechnung des
Frequenzverhaltens einer
elektronischen Schaltung
Vorgehen:
•
Erstellung eines Schaltbildes mit den Wechselspannungs- Ersatzschaltbildern der
Komponenten
•
Komplexe Wechselstromrechung zur Berechnung der gesuchten Größe bei
unterschiedlichen Frequenzen
Beispiele:
•
Ausgangspannung ua(ω)
•
Amplitudengang
Ausgangsspannung im Verhältnis zur Eingangsspannung)
Ua
Ue
Abbildung 4-2: Beispiel: Amplitudengang eines Butterworth- Filters, ω („Angular
frequency“) ist logarithmisch aufgetragen, die Verstärkung („Gain“)
Dezibel (dB).
Ua
in
Ue
Grundgebiete der Elektronik I, Bohn
Beispiel: Amplitudengang eines RC- Tiefpassfilters:
4.6-74
Grundgebiete der Elektronik I, Bohn
4.6-75
Amplitudengang (R=100000Ω=105Ω, C=1µF=10-6F):
ω
0
1
s
0
ω ⋅ R ⋅C
1
1
s
0,1
10
1
s
1
100
1
s
1000
10
100
1
A=
1 + ω 2 R 2C 2
Adb = 20 ⋅ log10 ( A)
A
1,0
0,1
0
0
0
1
1
10
s
s
0,16Hz 1,6Hz
1
1
s
16Hz
100
1
s
160Hz
1000
Wirkung auf 50Hz Störsignal:
Das 50Hz Störsignal wird um den Faktor
abgeschwächt!
ω
f
1
s
Grundgebiete der Elektronik I, Bohn
4.6.1
4.6-76
Beispiel: Nutzsignal mit Störsignal
Nutzsignal (langsam veränderlich)
Störsignal (50Hz Brummspannung)
Signal mit 50Hz Brumm 0,2V
2
1.5
u
1
0.5
0
-0.5
0
0.5
1
0
0.5
1
2
1.5
2
2.5
3
3.5
4
t
Signal nach Butterworth Tiefpass, fg=2Hz
1.5
2
4.5
5
4.5
5
1.5
u
1
0.5
0
-0.5
2.5
t
3
3.5
4
Grundgebiete der Elektronik I, Bohn
4.6.2
Überblick Filter
4.6-77
Grundgebiete der Elektronik I, Bohn
5.1-78
5 Schwingkreise
5.1 Differenzialgleichung der freien Schwingung
Prinzip einer Schwingung:
Beispiele:
1. Pendel (Uhrpendel)
potentielle Energie
(Gravitationsfeld)
Reibung
kinetische Energie
2. Feder mit Masse (Stoßdämpfer)
potentielle Federenergie
(mechanische Spannung)
Reibung
kinetische Energie
3. Violinsaite (Musikinstrument
potentielle Federenergie
(mechanische Spannung)
Reibung
kinetische Energie
4. Elektrischer Schwingkreis
Energie des elektrischen
Felds
Leiterverluste
Energie des magnetischen
Felds
Kapazitiv gespeicherte
Energie
Dielektrische Verluste
Induktiv gespeicherte
Energie
Magnetische Verluste
(Kondensator)
(Widerstand)
(Spule)
Grundgebiete der Elektronik I, Bohn
Berechnung des Schwingungsvorgangs mit Hilfe des Ersatzschaltbilds:
Mit t ≥ 0 gilt folgende Gleichung im Zeitbereich:
Damit wird die Differentialgleichung für den Strom:
Mit Kondensatorstrom i = C ⋅
du
in
dt
 du 
dC ⋅ 
du
dt 
uc + L ⋅ 
+ R ⋅C ⋅
=0
dt
dt
d 2u
du
=0
uc + L ⋅ C ⋅ 2c + R ⋅ C ⋅
dt
dt
⋅
1
LC
Differentialgleichung für die Spannung
d 2uc R ⋅ C duc
1
+
⋅
+
⋅ uc = 0
2
dt
L ⋅ C dt LC
5.1-79
Grundgebiete der Elektronik I, Bohn
5.1-80
D.h. Strom und Spannung haben den gleichen Zeitverlauf, allerdings unterschiedliche
Anfangswerte:
t = 0 → u c = u c max = U
→i =0
5.1.1.1
ANSATZ:
u c (t ) = U ⋅ e st
wegen uc(0)=U, Anfangsladung
Einsetzen in die DGL:
mit den Lösungen:
Wichtige Faktoren:
Dämpfung:
Eigenfrequenz:
Grundgebiete der Elektronik I, Bohn
5.1-81
Es ergeben sich 3 Fälle:
•
σ > ω0 :
uc(t) klingt exponentiell ab, (überkritisch gedämpft)
uc (t ) = c1 ⋅ e (−α + β )t + c2 ⋅ e (−α − β )t
wobei α = σ ; ω 0 =
c1 =
•
σ = ω0 :
1
LC
; β = α 2 − ω 02
α +β
−α + β
⋅ uˆ; c2 =
⋅ uˆ
2β
2β
uc(t) klingt exponentiell ab, (kritisch gedämpft, Aperiodischer
Grenzfall)
uc (t ) = (c1 + c2 ⋅ t ) ⋅ e −αt
wobei c1 = uˆ; c2 = α ⋅ uˆ
•
σ < ω0
uc(t) hat einen schwingenden Verlauf (Durchschwingen)
u c (t ) = e −σt ⋅ uˆ ⋅ (cos ωt + σω ⋅ sin ωt )
wobei Eigenfrequenz ω = ω 02 − σ 2
Grundgebiete der Elektronik I, Bohn
5.1-82
Praktisches Beispiel:
Ein Signal soll mit möglichst geringer Schaltverzögerung von IC1 an IC2 übertragen
werden.
Die Gesamtkapazität der Übertragungsstrecke ist 50pF (Ausgang IC1 20pF, Leitung
0,25m mit 40pF/m, Eingang IC2 20pF). Die Gesamt-Induktivität ist 12,5nH (Leitung
Länge 0,25m, Induktivitätsbelag 50nH/m).
Wie hoch ist optimale Widerstand für ein optimal schnelle Signalübertragung
(Aperiodischer Grenzfall?
Grundgebiete der Elektronik I, Bohn
5.1-83
u(t) 2V
1V
0V
10ns
20ns
Abbildung 5-1: Schwingungsverhalten in Abhängigkeit von R
t
Grundgebiete der Elektronik I, Bohn
5.2-84
5.2 Erzwungene Schwingung
Bisher: Aufladung eines Kondensators (Anfangszustand), Entladung, Umladung und
Schwingung in Form einer freien Schwingung
Jetzt: Anschluss eines Schwingkreises an eine sinusförmig veränderliche Quelle
(Strom- oder Spannungsquelle) -> erzwungene Schwingung
Bei sinusförmiger Erregung kann die komplexe Wechselstromrechnung eingesetzt
werden.
5.2.1.1
BEISPIEL:
Verhalten der Spannung am Kondensator:
Grundgebiete der Elektronik I, Bohn
5.2-85
Grundgebiete der Elektronik I, Bohn
1
Lineare Netzwerke......................................................................................... 1.1-1
1.1
Schreibweise: .......................................................................................... 1.1-1
1.2
Grundbegriff des Stromkreises ................................................................ 1.2-2
1.2.1
Materialeigenschaften ....................................................................... 1.2-2
1.2.2
Wirkungen des elektrischen Stroms .................................................. 1.2-3
1.3
Ersatzschaltbild des Stromkreises ........................................................... 1.3-4
1.3.1
Ersatzschaltbild mit idealer Spannungsquelle ................................... 1.3-4
1.3.2
Ersatzschaltbild mit idealer Stromquelle ........................................... 1.3-5
1.4
Der elektrische Widerstand ..................................................................... 1.4-6
1.4.2
1.5
2
5.2-86
Beispiele ........................................................................................... 1.4-7
Energie und Leistung............................................................................... 1.5-8
1.5.1
Energie ............................................................................................. 1.5-8
1.5.2
Leistung ............................................................................................ 1.5-9
Netzwerktheorie .......................................................................................... 1.5-10
2.1
Berechung von Netzwerken .................................................................. 2.1-11
2.1.1
Einfache Netzwerke ........................................................................ 2.1-11
2.1.2
Komplizierte Netzwerke (mit vielen Knoten).................................... 2.1-11
2.2
Ersatzschalbilder und Netzwerkelemente .............................................. 2.2-12
2.3
Gesetze für die Berechnung von Strom- und Spannungsverteilungen .. 2.3-13
2.3.1
Kirchhoffsche Knotenregel .............................................................. 2.3-13
2.3.2
Kirchhoffsche Maschenregel ........................................................... 2.3-15
2.3.3
Gleichungen der Netzwerkelemente ............................................... 2.3-16
2.3.4
Einfache Netzberechnungen ........................................................... 2.3-19
2.3.5
Parallelschaltungen ......................................................................... 2.3-22
2.4
Netzwerkumwandlungen ....................................................................... 2.4-26
2.4.1
Reihenschaltungen ......................................................................... 2.4-26
2.4.2
Parallelschaltungen ......................................................................... 2.4-27
2.4.3
Ersatzquellen .................................................................................. 2.4-30
Grundgebiete der Elektronik I, Bohn
3
2.4.4
Gesteuerte Quellen ......................................................................... 2.4-32
2.4.5
Leistungsanpassung ....................................................................... 2.4-33
Systematische Analyse linearer Netzwerke................................................. 2.4-37
3.1
Knotenspannungsverfahren .................................................................. 3.1-38
3.2
Netzwerkumwandlungen ....................................................................... 3.2-41
3.2.1
Vereinfachungen ............................................................................. 3.2-41
3.2.2
Behandlung von Spannungsquellen ............................................... 3.2-41
3.3
Auflösung nach den Knotenspannungen ............................................... 3.3-43
3.3.1
4
5.2-87
Beispiele: ........................................................................................ 3.3-45
Grundbegriffe der Wechselstromtechnik ..................................................... 3.3-48
4.1
Sinusförmige Wechselgrößen ............................................................... 4.1-48
4.2
Kennwerte ............................................................................................. 4.2-53
4.2.1
Periodendauer und Frequenz ......................................................... 4.2-53
4.2.2
Scheitelwert .................................................................................... 4.2-54
4.2.3
Effektivwert ..................................................................................... 4.2-55
4.2.4
Beschreibung sinusförmiger Wechselgrößen durch Kennwerte...... 4.2-56
4.3
Komplexe Rechnung, Zeigerdiagramme ............................................... 4.3-57
4.3.2
Zeigerdarstellung ............................................................................ 4.3-58
4.3.3
Zeiger in der komplexen Ebene ...................................................... 4.3-60
4.3.4
Rechenregeln für komplexe Größen ............................................... 4.3-61
4.3.5
Begriffe für das Rechnen mit komplexen Größen ........................... 4.3-65
4.4
Schaltungselemente in Wechselstromkreisen ....................................... 4.4-66
4.4.1
Der (Wirk-) Widerstand ................................................................... 4.4-66
4.4.2
Induktivität / Spule........................................................................... 4.4-67
4.4.3
Kapazität / Kondensator .................................................................. 4.4-68
4.5
Leistung und Energie............................................................................. 4.5-69
4.5.1
4.6
Beschreibung im Zeitbereich........................................................... 4.5-69
Berechnung des Frequenzverhaltens einer elektronischen Schaltung .. 4.6-73
Grundgebiete der Elektronik I, Bohn
5
5.2-88
4.6.1
Beispiel: Nutzsignal mit Störsignal .................................................. 4.6-76
4.6.2
Überblick Filter ................................................................................ 4.6-77
Schwingkreise ............................................................................................. 4.6-78
5.1
Differenzialgleichung der freien Schwingung ......................................... 5.1-78
5.2
Erzwungene Schwingung ...................................................................... 5.2-84