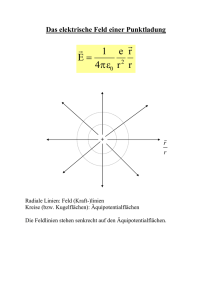
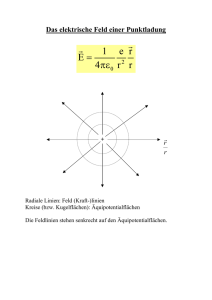
Elektrisches Potential
Werbung

Einführung in die Physik II für Studierende der Naturwissenschaften und Zahnheilkunde Sommersemester 2007 VL #6 am 02.05.2007 Vladimir Dyakonov Elektrisches Potential Wieviel Arbeit muss ich aufwenden um eine Ladung vom Unendlichen zu einem Punkt r zu bringen? Durch Verschieben gewinnt Ladung potentielle Energie. Frage: Kann ich ein Größe definieren, die mir ladungsunabhänig den Zustand in einem Punkt beschreibt? Ja das elektrische Potenzial elektrisches Potential = potentiell e Energie Ladung 1 Elektrisches Potential Das elektrische Potenzial gibt an, welche potentielle Energie eine Probeladung in einem Punkt hat, nachdem sie in einem vorgegebenen elektrischen Feld vom Unendlichen zu einem Punkt gebracht wurde. Die Potentialdifferenz ist ein Maß für die Arbeit die aufgewendet werden muss, um eine Ladung in einem elektrischen Feld von einem Punkt zum anderen zu bringen Elektrisches Potential Wieviel Arbeit muss ich aufwenden um eine Ladung vom Unendlichen zu einem Punkt r zu bringen? Durch Verschieben gewinnt Ladung potentielle Energie. Frage: Kann ich ein Größe definieren, die mir ladungsunabhänig den Zustand in einem Punkt beschreibt? Ja das elektrische Potenzial elektrisches Potential = potentiell e Energie Ladung 2 Elektrisches Potential Das elektrische Potenzial gibt an, welche potentielle Energie eine Probeladung in einem Punkt hat, nachdem sie in einem vorgegebenen elektrischen Feld vom Unendlichen zu einem Punkt gebracht wurde. Die Potentialdifferenz ist ein Maß für die Arbeit die aufgewendet werden muss, um eine Ladung in einem elektrischen Feld von einem Punkt zum anderen zu bringen Potential einer Punktladung Wie berechnet man das Potential einer Punktladung Q ? Q r q0 Arbeit um Probeladung q0 vom Unendlichen auf Abstand r zu bringen 3 Potential einer Punktladung 4 Potentialdifferenz Potentialdifferenz zwischen zwei Punkten U12 = ϕ(1) - ϕ(2) Spannung Einheit [U] = J/C Joule pro Coulomb bzw. Nm/As oder V Volt Arbeit W = q U = Ladung mal Potentialdifferenz Eine Probeladung qo im Feld E erfährt eine Kraft; Bewegung der Ladung gegen diese Kraft benötigt die Verrichtung von Arbeit: W = ∫ F⋅dr = ∫ qo E⋅dr Mit E = (1/4πεo) q1/r2 oder W/qo = ∫ E⋅dr. (Coulomb-Feld): W/qo = ∫ E⋅dr = (1/4πεo) q1 ∫ dr/r2 = -(1/4πεo) q1/r. Das ist ein Maß für die Arbeit und heißt 'Coulomb-Potential' der Punktladung q1. Allgemein: die Arbeit bzw. die Energie einer Ladung, geteilt durch die Ladungsmenge, nennt man das elektrische Potential ϕ: ∆ϕ = -∫ E⋅dr. 5 Feldlinien und Potential Die elektrischen Feldlinien zeigen in die Richtung, in der das Potential abnimmt. Arbeit im Schwerefeld und im elektrischen Feld • • • positive Probeladung q0 im elektrisches Feld E, wird in Richtung des Feldstärkevektors beschleunigt Potentielle Energie U nimmt ab Kinetische Energie K nimmt zu 6 Äquipotentiallinien / -flächen Höhenlandschaft in der Mechanik Die Höhenkontourlinien (rot) verbinden Punkte der gleichen Höhe h; darauf bewegt sich eine Masse m ohne Arbeit, ihre potentielle Energie mgh bleibt konstant. Linien der maximalen Steigung (grün) zeigen senkrecht zu den Höhenkontouren, eine Masse würde entlang solcher Linien hinunterrollen. Die Kraft zeigt in Richtung der maximalen Steigung und wächst mit wachsender Steigung (d.h. wenn die Höhenkontouren dicht zusammen liegen). 7 Äquipotentiallinien Eine elektrische 'Potentiallandschaft' gleicht einer Höhenlandschaft in der Mechanik Merke: Äquipotentiallinien und Feldlinien stehen normal aufeinander Äquipotentialflächen Äquipotentialfläche: Feldstärkevektor ⊥ Äquipotentialflächen V =constant= 0 8 Experimentelle Bestimmung von Potentiallinien 15V/5A v Tisch F Messfühler Tableau B A F5 B5 PM 2535 0.00 V Messspitze x B6 Beispiel: Potential in einem Plattenkondensator y - F6 E Feld d + Plattenkondensator Elektrisches Feld E homogen d.h. überall gleich nach Betrag und Richtung E( r) = E = U/d U angelegte Spannung d Abstand ϕ= ∫ E ( x )dx = Ex = U x + const d U Äquipotentiallinien ϕ = Konstant Parallele Linien in y-Richtung 9 Potential Plattenkondensator Äquipotentiallinien für ∆ϕ = 2V U=8V Potentialnullpunkt frei gewählt!!! Arbeit im Plattenkondensator x y A Welche Arbeit muss zum Transport einer Ladung q von Punkt A nach Punkt B aufgewendet werden? Arbeit hängt nur von der Potentialdifferenz ab, und ist wegunabhängig. B WAB = q (ϕA - ϕB) Arbeit entlang x und y Richtung: Arbeit = F r = q E r Vektorprodukt A B = A B wenn A || B A B = 0 wenn A ⊥ B y Richtung normal zu E-Feld und parallel zu Äquipotentiallinien Wy = 0 x Richtung parallel zu E-Feld und Normal zu Äquipotentiallinien Wx = q E x 10 Zusammenhang E-Feld und Potential Wir können die obige Beziehung zwischen Potential und Feld umkehren, um das Feld aus dem Potential zu berechnen: E(r) = -d/dr [ϕ(r)] (eindimensional; z.B. beim Feld einer Punktladung oder homogenes Feld in Richtung r); oder (dreidimensional): E(r) = -∇ ϕ(r) ∇ ist die Abkürzung für eine dreidimensionale Ableitung, die als Vektor in Richtung maximaler Steigung zeigt. Man nennt dies 'Gradientenbildung' und schreibt : E(r) = -grad [ϕ(r)] . 11