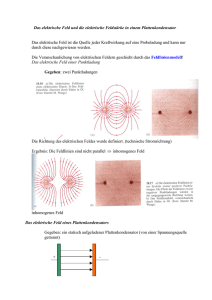
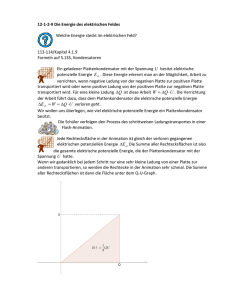
Das elektrische Potential und die Spannung

Das elektrische Potential und die Spannung
Der Quotient aus der potentiellen Energie W und der Ladung Q wird auch als elektrisches
Potential ϕ bezeichnet:
W
.
Q
Die Potentialdifferenz ist unabhängig von der Wahl des Potentialnullpunktes.
Je größer die Potentialdifferenz zwischen zwei Punkten ist (Abstand zwischen zwei
Ladungen), desto größer ist die Arbeit W, die aufgebracht werden muss, um eine bestimmte
Probeladung Q von einer platte zu einer anderen zu bewegen; desto mehr Energie wird aber
auch frei, wenn sich eine Ladung von einer Platte zur anderen im elektrischen Feld bewegt. Je
größer die Potentialdifferenz ist, desto stärker ist das Bestreben der Ladungen auf beiden
Platten, sich auszugleichen.
Diese Potentialdifferenz zwischen zwei Punkten nennt man die elektrische Spannung.
ϕ=
U 1, 2 = ∆ϕ 1.2 =
Einheit:
Da U =
∆W1→ 2
Q
VAs
⎡ J
⎤
⎢⎣1 C = 1 As = 1V ⎥⎦ Volt
W Q⋅E⋅d
=
für den Plattenkondensator gilt, ergibt sich:
Q
Q
U
für die elektrische Feldstärke in einem Plattenkondensator.
E=
d
Aufgabe 1
An einem Plattenkondensator ist die Spannung U = 1000V angelegt. Auf eine Probeladung
Q = 10 −9 C wirkt eine Kraft F = 5 ⋅ 10 −4 N . Bestimmen Sie die Feldstärke und den
Plattenabstand.
Lösung:
E=
F 5 ⋅ 10 −4 N
N
V
=
= 5 ⋅ 10 5
= 5 ⋅ 10 5 .
−9
Q
C
m
10 C
Aus d =
U
10 3 V
erhalten wir d =
= 0,002m .
E
5 V
5 ⋅ 10
m
Aufgabe 2
Zwischen zwei vertikalen Platten von 6 cm Abstand herrscht eine Spannung von 5400 V.
Unmittelbar vor der positiven Platte wird ein kleines Kügelchen der Masse m = 0,5 g und der
Ladung Q = 5 ⋅ 10 −9 C aus der Ruhe losgelassen. Mit welcher Geschwindigkeit und nach
welcher Zeit trifft der Körper auf die negative Platte, wenn die Gewichtskraft und der
Luftwiderstand vernachlässigt werden können?
Lösung:
Da zwischen den Platten ein homogenes Feld vorhanden ist, gilt:
U 5400V
V
E= =
= 90000 .
d 0,06m
m
Aus dem Energieerhaltungssatz folgt:
1
m ⋅ v 2 = Q ⋅ U mit E elek = Q ⋅ U
2
2 ⋅ Q ⋅U
m
und damit v =
= 0,3 .
m
s
Die Beschleunigung erhalten wir mit Hilfe der Grundgleichung der Mechanik: F = m ⋅ a .
a=
F Q⋅E
m
=
= 0,9 2
m
m
s
Schließlich erhalten wir die Zeit aus a =
t=
v
= 0,37 s .
a
v
:
t