Die geradlinig gleichförmige Bewegung

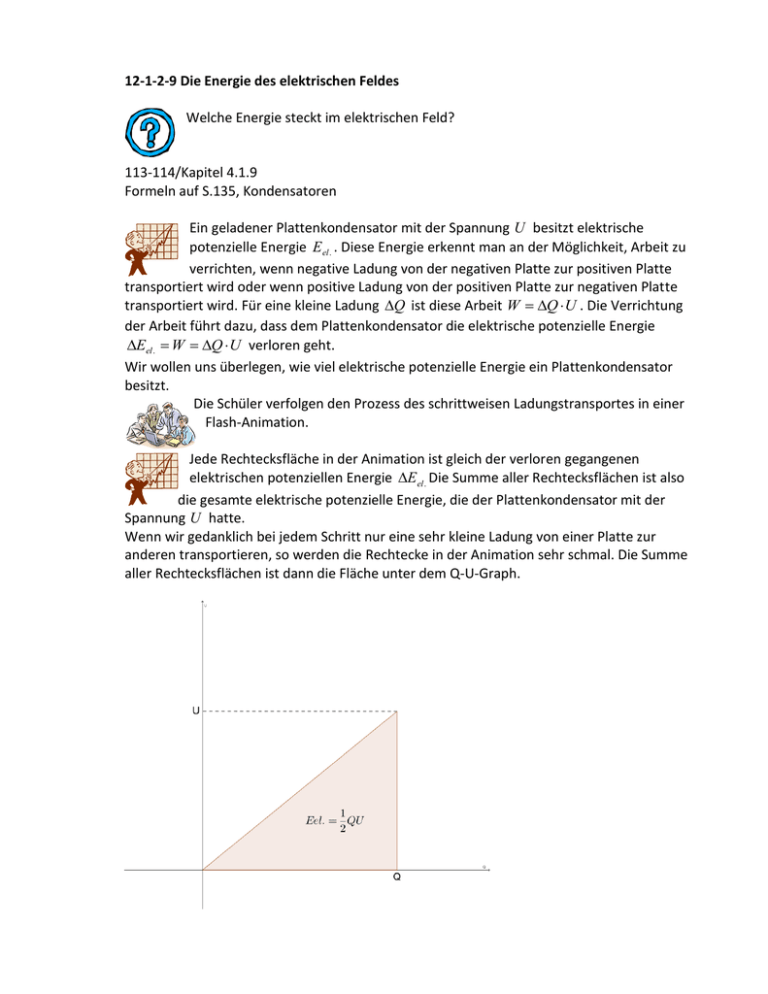
12-1-2-9 Die Energie des elektrischen Feldes
Welche Energie steckt im elektrischen Feld?
113-114/Kapitel 4.1.9
Formeln auf S.135, Kondensatoren
Ein geladener Plattenkondensator mit der Spannung U besitzt elektrische
potenzielle Energie E el . . Diese Energie erkennt man an der Möglichkeit, Arbeit zu
verrichten, wenn negative Ladung von der negativen Platte zur positiven Platte
transportiert wird oder wenn positive Ladung von der positiven Platte zur negativen Platte
transportiert wird. Für eine kleine Ladung Q ist diese Arbeit W  Q  U . Die Verrichtung
der Arbeit führt dazu, dass dem Plattenkondensator die elektrische potenzielle Energie
Eel .  W  Q  U verloren geht.
Wir wollen uns überlegen, wie viel elektrische potenzielle Energie ein Plattenkondensator
besitzt.
Die Schüler verfolgen den Prozess des schrittweisen Ladungstransportes in einer
Flash-Animation.
Jede Rechtecksfläche in der Animation ist gleich der verloren gegangenen
elektrischen potenziellen Energie Eel . Die Summe aller Rechtecksflächen ist also
die gesamte elektrische potenzielle Energie, die der Plattenkondensator mit der
Spannung U hatte.
Wenn wir gedanklich bei jedem Schritt nur eine sehr kleine Ladung von einer Platte zur
anderen transportieren, so werden die Rechtecke in der Animation sehr schmal. Die Summe
aller Rechtecksflächen ist dann die Fläche unter dem Q-U-Graph.
Wegen Q  C  U gilt
Die elektrische Energie eines Kondensators ist
Eel . 
1
1
Q U  C U 2
2
2
Die elektrische Energie des Kondensators wird in der Regel dem elektrischen Feld E
zugeschrieben, das zwischen den Kondensatorplatten besteht.
A
Beim Plattenkondensator gilt U  E  d und C   0   r  .
d
Die elektrische Energie des elektrischen Feldes E im Plattenkondensator ist
Eel . 
1
1
C U 2   0   r  A  d  E 2
2
2
1. Sieh den Film zur spontanen Energieentladung eines großen Kondensators.
2. (Nach Grundkursabitur Bayern 1997)
Ein Plattenkondensator mit quadratischen Platten der Kantenlänge s = 14 cm und
dem Plattenabstand d1 = 20 mm wird an eine Gleichspannungsquelle mit U1 = 80V
angeschlossen. Nachdem der Kondensator geladen wurde, wird er von der
Spannungsquelle getrennt.
a. Berechnen Sie die Ladung Q1 auf einer Kondensatorplatte und die elektrische
Feldstärke E1 im Raum zwischen den Platten. [zur Kontrolle: Q1 = 6,9·10-10C] (6 BE)
b. Der Plattenabstand wird nun auf d2 = 15mm verringert.
Wie groß ist jetzt die zwischen den Platten bestehende Spannung U2? (4 BE)
c. Berechnen Sie die Änderung ΔWel der im Kondensator gespeicherten elektrischen
Feldenergie infolge der Änderung des Plattenabstands von d 1 auf d2. (4 BE)
1.
2.
0,14m  8,67  10 12 As . Da keine
A
As
 8,85  10 12
1
d
Vm
0,02m
V
Angaben zu einem Dielektrikum im Kondensator vorliegen, gehen wir davon aus,
das sich Luft zwischen den Platten befindet und setzen  r  1 .
As
 80V  6,94  10 10 As
Es ergibt sich Q  C  U  8,67  10 12
V
U
80V
V
E 
 4000
d 0,02m
m
V
b. U 2  E  d  4000  0,015m  60V
m
1
1
1
As
80V 2  60V 2  1,21  10 8 J
c. Eel .  C  U 12  C  U 22   8,67  10 12
2
2
2
V
2
a. Q  C  U mit C   0   r 

