4. Vorlesung

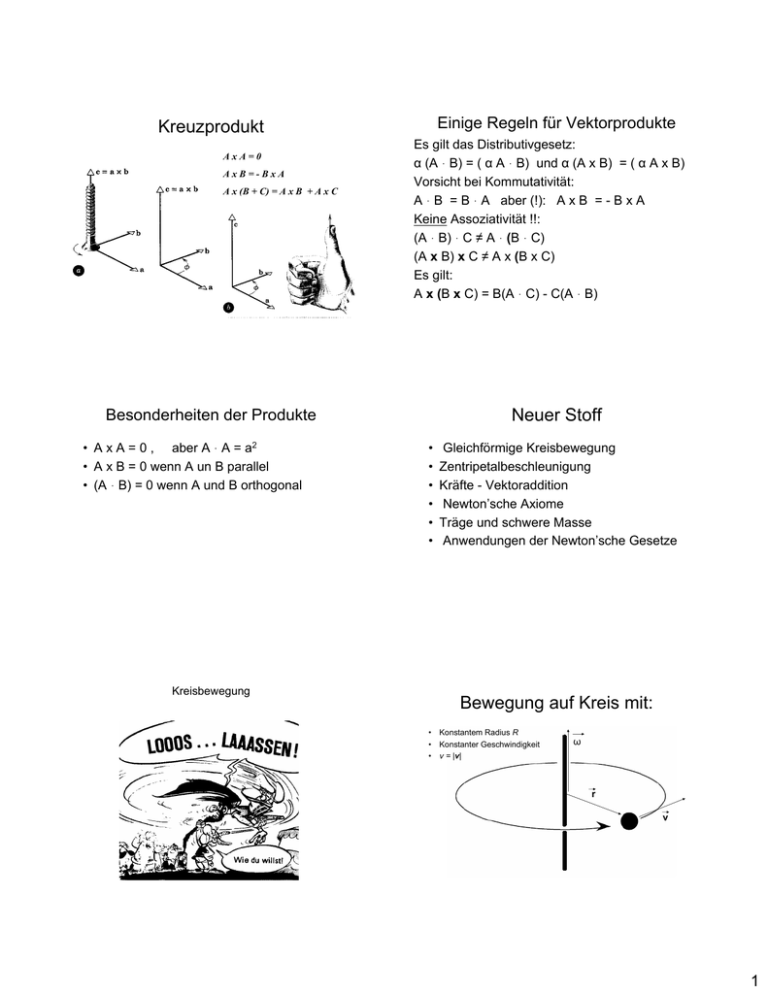
Einige Regeln für Vektorprodukte
Kreuzprodukt
AxA=0
AxB=-BxA
A x (B + C) = A x B + A x C
Es gilt das Distributivgesetz:
α (A ּ B) = ( α A ּ B) und α (A x B) = ( α A x B)
Vorsicht bei Kommutativität:
A ּ B = B ּ A aber (!): A x B = - B x A
Keine Assoziativität !!:
(A ּ B) ּ C ≠ A ּ (B ּ C)
(A x B) x C ≠ A x (B x C)
Es gilt:
A x (B x C) = B(A ּ C) - C(A ּ B)
Neuer Stoff
Besonderheiten der Produkte
• A x A = 0 , aber A ּ A = a2
• A x B = 0 wenn A un B parallel
• (A ּ B) = 0 wenn A und B orthogonal
Kreisbewegung
•
•
•
•
•
•
Gleichförmige Kreisbewegung
Zentripetalbeschleunigung
Kräfte - Vektoraddition
Newton’sche Axiome
Träge und schwere Masse
Anwendungen der Newton’sche Gesetze
Bewegung auf Kreis mit:
• Konstantem Radius R
• Konstanter Geschwindigkeit
• v = |v|
ω
r
v
1
Kreisbewegung mit konstanter Winkelgeschwindigkeit
Wahl des Koordinatensystems
» Kartesisch:
• – (x,y) [Position]
• – (vx ,vy) [Geschwindigkeit]
a ist die Zentripetalbeschleunigung
(zum Zentrum hin)
Bogenlänge s
» Polar:
• (R,θ) [Position]
• (vR ,ω) [Geschwindigkeit]
• R konstant (daher vR = 0).
• ω (Winkelgeschwindigkeit)
konstant.
Polar Koordinaten passen zu
Kreisbewegung
Änderung der Geschwindigkeit =
Beschleunigung
=> hat einfache Beziehung
zum Winkel:
s=Rθ
wobei θ die Winkeländerung ist.
Einheit von θ ist Radiant
Für eine Umdrehung gilt:
2πR = Rθc
θc = 2π
=> θ hat Periode 2π.
∆t, ∆v / ∆t -> 0 :
dv / dt = a
a zeigt in Richtung - R
1 Umdrehung = 2π Radiant
a = v2 /R
Ähnliche Dreiecke:
∆v /v = ∆R /R
Mit
a = v2 /R
und v = ω R
Für kleine ∆t :
∆R = v∆t
folgt
Damit:
∆v /v= v∆t /R
und
∆v / ∆t = v2 /R
a = (ω R ) 2 /R
= ω 2R
2
Addition der wirkenden Kräfte
Zentripetalbeschleunigung des Mondes
T = 27.3 Tage = 2.36 x 106
(Periode ~ 1 Monat)
R = 3.84 x 108 m (Abstand zum Mond)
RE = 6.35 x 106 m (Erdradius)
Zentripetalkraft
Gewicht
Winkelgeschwindigkeit:
ω = 2π 1/T = 2.66 x 10-6 s-6
Beschleunigung :
a = ω2R = 0.00272 m/s2 = 0.000278 g
Richtung von a : zeigt zum Zentrum der Erde (-r ).
Frage
Das Spaceshuttle ist im erdnahen Orbit etwa 300 km über der
Erdoberfläche. Die Periode der Umlaufbahn ist etwa 91 min. Wie groß
ist die Beschleunigung eines Astronauten im Shuttle im Bezugssystem
der Erde?
(Der Erdradius beträgt 6.4 x 106 m)
Newton bemerkte, dass
amoon / g = 0.000278
(a) 0 m/s2
(b) 8.9 m/s2
(c) 9.8 m/s2
ungefähr dem Verhältnis
RE2 / R2 = 0.000273
entspricht, und schloss daraus
F ∝ 1 / R2
Rechenweg
Ergebnis
1. Winkelgeschwindigkeit:
ω = (1rot / 91min) x (1 min / 60 s) x (2 π rad/rot)
= 6,28 / 5460 s = 0,00015 s-1
2. Bahnradius
RO = RE + 300 km
= 6.4 x 106 m + 0.3 x 106 m = 6.7 x 106 m
3
Addition von Kräften
Die Newtonschen Gesetze
1.Newtonsches Gesetz
Ein Körper, auf den keine äußeren Kräfte einwirken, verharrt
Körper verharrt im Zustand der Ruhe oder gleichförmigen
Bewegung, falls keine äußeren Kräfte auf ihn einwirken.
Die zeitliche Änderung des Impulses ist die äußere Kraft.
p = mv
(Definition des Impulses)
F = d/dt p = d/dt(mv) = dm/dt v + m dv/dt (Def. der Kraft)
meistens : FNET = ΣF = ma
im Zustand der Ruhe oder gleichförmigen Bewegung.
Gilt in Bezug auf ein Inertialsystem.
Ohne Krafteinwirkung gibt es keine Beschleunigung:
» Ein Inertialsystem (IS) ist ein unbeschleunigtes (oder
nicht rotierendes) Bezugssystem in Bezug auf
“Fixsterne”.
» Falls ein IS existiert, existierten unendlich viele, die sich
nur durch eine konstante Geschwindigkeit unterscheiden.
actio = reactio: FA ,B = - FB ,A
2. Newtonsches Gesetz
3. Newtonsches Gesetz
FNET = Σ F = ma.
Die Beschleunigung a eines Objektes ist
proportional zu der darauf wirkenden Kraft FNET
» Proportionalitätskonstante ist die “Masse”, m.
– Dies ist Definition der (trägen) Masse.
– Die Masse eines Objekts ist eine konstante Eigenschaft
Einheit der Kraft [M]x[L / T2] = kg m/s2 = N (Newton)
Einheit des Impulses p = m v [M]x[L / T] = kg m/s
4