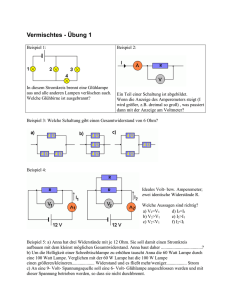
Station 1 A (Reihenschaltung) Station 1 B (Reihenschaltung) Station

Station 1 A (Reihenschaltung)
(a) Die Reihenschaltung von Widerständen aus einem
100 Ω
und einem
500 Ω
Widerstand liegt an einer Spannungsquelle. An welchem Widerstand liegt
die gröÿere Spannung? Was lässt sich über die Stromstärken durch die Widerstände aussagen?
(b) Durch die Reihenschaltung der Widerstände
von
0, 05 A.
200 Ω und 100 Ω ieÿt ein Strom
Berechne die an den Widerständen liegenden Spannungen. Wie
groÿ ist die Gesamtspannung?
Station 1 B (Reihenschaltung)
Zwei Widerstände mit
47 Ω
bzw.
100 Ω
werden an eine Stromquelle mit einer
Spannung von 6,0 V angeschlossen, und zwar in Reihe geschaltet.
(a) Zeichne ein zugehöriges Schaltbild. Zeichne in das Schaltbild auch Messgeräte
zur Messung der an den Widerständen anliegenden Spannung ein.
(b) Berechne jeweils die an den Widerständen anliegende Spannung und die
durch die Widerstände ieÿende Stromstärke sowie den Gesamtwiderstand
der Schaltung.
Station 1 C (Reihenschaltung)
Zwei Widerstände von
47 Ω
und
100 Ω
sind mit einer elektrischen Quelle in Reihe
geschaltet.
(a) Am Widerstand mit
47 Ω
liegt eine Spannung von 6,0 V an. Wie groÿ ist die
Spannung am anderen Widerstand?
(b) Welche Spannung hat die Quelle?
Station 1 A (Reihenschaltung) Lösung
(a) Für die Reihenschaltung gilt:
Am gröÿeren Widerstand liegt auch die gröÿere Spannung an. Die Spannung
teilt sich im Verhältnis der Widerstände auf, hier ist das Verhältnis
Die Spannung am
500 Ω
100 Ω
=
5
1.
500 Ω-Widerstand ist also 5-mal so groÿ wie die Spannung
am anderen Widerstand.
Die Stromstärke ist an jeder Stelle des Stromkreises gleich groÿ. Durch die
Widerstände ieÿt also die gleiche Stromstärke.
(b) Die Spannung am ersten Widerstand
R1 = 200 Ω
beträgt
U1 = R1 · I = 200 Ω · 0, 05 A = 10 V.
Die Spannung am zweiten Widerstand
R2 = 100 Ω
beträgt
U2 = R2 · I = 100 Ω · 0, 05 A = 5, 0 V.
Die Gesamtspannung ist
Uges = U1 + U2 = 10 V + 5 V = 15 V.
Station 1 B (Reihenschaltung) Lösung
(a) Schaltbild:
(b) Gesamtwiderstand: Da es sich um eine Reihenschaltung handelt, erhält man
den Gesamtwiderstand
Rges
durch Addition der einzelnen Widerstände:
Rges = R1 + R2 = 47 Ω + 100 Ω = 147 Ω
Die (Gesamt-)Stromstärke
Rges =
Iges
ist an jeder Stelle im Stromkreis gleich, aus
Uges
Iges folgt
Iges =
6V
Uges
=
≈ 0, 0408 A = 40, 8 mA
Rges
147 Ω
U1 = Iges · R1 ≈ 1, 92 V
U2 = Iges · R2 ≈ 4, 08 V
Am ersten Widerstand liegt dann die Spannung
und am zweiten Widerstand
an
Station 1 C (Reihenschaltung) Lösung
R2 : R1 = 100 Ω : 47Ω. Also gilt auch für das Verhältnis der Spannung
U2 am Widerstand R2 zur Spannung U1 am Widerstand R1 :
(a) Es ist
U2 : U1 = 100 : 47,
also
U2 =
100
47
· 6, 0 V ≈ 12, 8 V.
(b) Die einzelnen Spannungen addieren sich zur Gesamtspannung, die Stromquelle hat somit die Spannung
6, 0 V + 12, 8 V = 18, 8 V.
Station 2 A (Parallelschaltung)
Ein Motor und eine Glühlampe sind in einem Stromkreis parallel geschaltet.
Wie groÿ sind die Stromstärken
I3
und
I4 ?
Begründe!
Station 2 B (Parallelschaltung)
Ein Stromkreis besteht aus zwei parallel geschalteten Widerständen mit den Werten
R1 = 47 Ω
sowie
R2 = 100 Ω
und einer Quelle mit 12 V.
Zeichne ein Schaltbild und berechne die Stromstärken und die Spannungen.
Station 2 C (Parallelschaltung)
Heinz-Rüdiger hat einen Elektrobaukasten bekommen und erweitert zur Freude seiner Oma deren elektrischen Adventskranz um weitere Kerzen. Beim Einschalten der
7.Kerze beginnt es, verschmort zu riechen.
(a) Was ist die Ursache dieser Beobachtung?
(b) Wie groÿ ist der Gesamtwiderstand am 7. Advent , wenn eine Glühbirne
hat?
16 Ω
Station 2 Z (Parallelschaltung)
Welcher der angegeben Widerstände ist der Gesamtwiderstand der Schaltung? Versuche die Aufgabe durch logische Argumentation und Abschätzung zu lösen, eine
aufwändige Rechnung ist nicht nötig.
• 48 Ω
• 240 Ω
• 620 Ω
• 1140 Ω
• 1860 Ω
Station 2 A (Parallelschaltung) Lösung
Die Stromstärken
I1
und
I4
sind gleich groÿ, sie geben die Gesamtstromstärke
im Stromkreis an, also:
I4 = I1 = 2, 5 A.
Da sich
I2
und 3 zur Gesamtstromstärke addieren, gilt:
I1 = I2 + I3 ,
I3 = I1 − I2 = 2, 5 A − 0, 4 A = 2, 1 A.
also
Station 2 B (Parallelschaltung) Lösung
Schaltbild:
An beiden Widerständen liegt die Gesamtspannung
stärke
I1
R1
durch den Widerstand
I1 =
Und die Stromstärke
I2
Uges = 12 V
an. Die Strom-
ist also
12 V
Uges
=
≈ 0, 25 A.
R1
47 Ω
beträgt
I2 =
Uges
12 V
=
= 0, 12 A.
R2
100 Ω
Die Gesamtstromstärke ist demnach
Iges = I1 + I2 = 0, 37 A.
Zur Berechnung des Gesamtwiderstands: Da es sich um eine Parallelschaltung
handelt, ist
1
1
1
1
1
100
47
147
=
+
=
+
=
+
=
Rges
R1 R2
47 Ω 100 Ω 4700 Ω 4700 Ω 4700 Ω
und somit
Rges =
4700 Ω
147
≈ 32, 0 Ω.
Alternative: Wenn man schon die Gesamtstromstärke berechnet hat, geht es natürlich viel einfacher. Der Gesamtwiderstand ist
Rges =
Uges
12 V
=
≈ 32 Ω.
Iges
0, 37 A
Station 2 C (Parallelschaltung) Lösung
(a) Der Gesamtwiderstand wird bei dieser Parallelschaltung mit jeder Kerze, die
dazukommt, kleiner! Dadurch erhöht sich die Gesamtstromstärke. (Die Gesamtstromstärke ist ja die Summe der Stromstärken in den einzelnen Ästen,
mit jeder Kerze, die dazu kommt, erhöht sie sich also um diesen Betrag).
Irgendwann wird die Stromstärke zu groÿ...
(b) Für den Gesamtwiderstand
Rges
gilt:
1
1
1
1
1
1
1
7
1
=
+
+
+
+
+
+
=
.
Rges
16 Ω 16 Ω 16 Ω 16 Ω 16 Ω 16 Ω 16 Ω 16 Ω
und somit
Rges =
16 Ω
≈ 2, 29 Ω.
7
Station 2 Z (Parallelschaltung) Lösung
Der Gesamtwiderstand ist kleiner als
muss also etwa
48 Ω
betragen.
jeder der beteiligten Einzelwiderstände, er
Station 3 A (Schaltungsskizzen)
Die Kerzen einer elektrischen Christbaumbeleuchtung benötigen zum Leuchten jeweils eine Spannung von 22 V. Die Netzspannung beträgt 220 V. Zeichne das dazugehörige Schaltbild. Begründung!
Station 3 B (Schaltungsskizzen)
Wie muss man zwei 5 V-Lämpchen an eine 5,0 V-Batterie anschlieÿen, damit beide
mit ihrer normalen Helligkeit leuchten? Begründung!
Station 3 C (Schaltungsskizzen)
Es stehen Widerstände mit
2, 0 Ω, 5, 0 Ω, 10 Ω
Wie erhält man einen Gesamtwiderstand von
Zeichne das zugehörige Schaltbild.
50 Ω zur Verfügung.
10
Ω ≈ 1, 4 Ω bzw. von ca. 16, 5 Ω?
7
und
Station 3 A (Schaltungsskizzen) Lösung
Man muss 10 Kerzen in Reihe schalten.
Station 3 B (Schaltungsskizzen) Lösung
Man muss die beiden Batterien parallel schalten. Dann liegt an jedem Lämpchen
die Spannung von 5 V. (Bei Reihenschaltung würde an jedem Lämpchen nur eine
Spannung von 2,5 V anliegen)
Station 3 C (Schaltungsskizzen) Lösung
Für
10
7 Ω: Zum Beispiel einen
Für
16, 5 Ω:
2, 0Ω
und einen
5, 0 Ω
Widerstand parallel schalten.
Station 4 A (Vergleich von Parallel- und Reihenschaltung)
Du siehst auf dieser Seite eine zum groÿen Teil leere Tabelle. Füge in die leeren
Felder der Tabelle die richtigen nummerierten Felder ein.
Reihenschaltung
Skizze
Spannung
Stromstärke
Widerstand
Verhalten
von
Glühlampen
Anwendungen
Gleichungen
Parallelschaltung
1)
U1 = U2 = · · · = Un = Uges
3)
4) Wenn man eine Glühlampe
2) I1 + I2 + . . . + In = Iges
5) Mehrfachsteckdosen; Be-
herausdreht, leuchten die an-
lasteter Spannungsteiler
ren sich zum Gesamtwider-
U1 + U2 + . . . + Un = Uges
deren Lampen weiter
7)
6) Die Teilwiderstände addiestand.
8)
9) Die Teilspannungen addieren sich zur Gesamtspannung
10) Der Gesamtwiderstand ist
11) Die Spannung an jedem
kleiner als der kleinste Einzel-
Widerstand ist gleich groÿ
12) R
1
+ R12 + · · · + R1n =
15) I1
= I2 = · · · = In
1
1
Rges
widerstand
13)
R1 + R2 + · · · + Rn = Rges
14) Wenn man eine Glühlampe herausdreht, gehen alle anderen Lampen aus.
16) Die Teilstromstärken ad-
17)
dieren sich zur Gesamtstrom-
nungsprüfer
stärke.
Lichterketten;
Span-
18) Die Stromstärke ist an
jeder Stelle des Stromkreises
gleich groÿ.
Station 4 B (Vergleich von Parallel- und Reihenschaltung)
An eine Batterie ist zunächst eine Lampe angeschlossen, sie leuchtet in normaler
Helligkeit.
(a) Was ändert sich, wenn eine zweite gleichartige Lampe in Serie zur bereits
vorhandenen Lampe geschaltet wird? Ausführliche Begründung!
(b) Was ändert sich, wenn eine zweite gleichartige Lampe parallel zu der vorhandenen Lampe geschaltet wird? Ausführliche Begründung!
Gehe bei beiden Fragen auch darauf ein, ob die Batterie mehr oder weniger
Strom liefern muss als im Fall von nur einer angeschlossenen Lampe.
Station 4 A (Parallel- und Reihenschaltung) Lösung
Reihenschaltung
Parallelschaltung
Skizze
7)
8)
Spannung
9) Die Teilspannungen ad-
11) Die Spannung an jedem
dieren sich zur Gesamtspan-
Widerstand ist gleich groÿ
nung
Stromstärke
Widerstand
Verhalten
von
Glühlampen
Anwendungen
18) Die Stromstärke ist an
16) Die Teilstromstärken ad-
jeder Stelle des Stromkreises
dieren
gleich groÿ.
stromstärke.
6) Die Teilwiderstände ad-
10)
dieren sich zum Gesamtwi-
ist kleiner als der kleinste
derstand.
Einzelwiderstand
14) Wenn man eine Glüh-
4) Wenn man eine Glühlam-
lampe herausdreht, gehen al-
pe herausdreht, leuchten die
le anderen Lampen aus.
anderen Lampen weiter
17)
5) Mehrfachsteckdosen; Be-
Lichterketten;
Span-
nungsprüfer
Gleichungen
Der
sich
zur
Gesamt-
Gesamtwiderstand
lasteter Spannungsteiler
U1 + U2 + . . . + Un = Uges 3) U1 = U2 = · · · = Un =
15) I1 = I2 = · · · = In
Uges
13) R1 +R2 +· · ·+Rn = Rges 2) I1 + I2 + . . . + In = Iges
1
1
1
1
12)
R1 + R2 + · · · + Rn = Rges
1)
Station 4 B (Parallel- und Reihenschaltung) Lösung
(a) Durch die Serienschaltung der beiden Lampen erhöht sich der Gesamtwiderstand der Schaltung. Da die Spannung der Batterie gleich bleibt, sinkt
dadurch der Strom. Beide Lampen leuchten gleich hell. Die ursprünglich vorhandene Lampe jedoch schwächer als vorher.
(b) Bei der Parallelschaltung der beiden Lampen liegt an jeder die Batteriespannung. Der Strom in der Hauptleitung verdoppelt sich. Beide Lampen leuchten
gleich hell. Die ursprünglich vorhandene Lampe behält ihre Helligkeit bei.
Station 5 A (Schutzwiderstand)
Leuchtdioden lösen in vielen Bereichen die Glühlampen als Lichtquellen ab, da ihre Lichtausbeute deutlich höher ist als die von Glühlampen. Von einer Leuchtdiode weiÿ man, dass im Betriebszustand der durch sie ieÿende Strom maxi-
Imax = 30 mA sein darf. In diesem Fall liegt an der Leuchtdiode die Spannung Udiode = 1, 5 V. Die Leuchtdiode soll nun an eine Gleichspannungsquelle von
Ubatt = 6, 0 V angeschlossen werden.
mal
(a) Wie kann man mit einem Widerstand geeigneter Gröÿe vorsorgen, dass die
Leuchtdiode nicht zerstört wird? Schaltskizze und Begründung!
(b) Berechne die Gröÿe des Widerstandswertes.
Station 5 B (Schutzwiderstand)
Ein Signallämpchen einer Eisenbahnanlage hat folgende Kenndaten: 4,0 V; 0,10 A.
Es steht in der Anlage jedoch eine Spannung von 9,0 V zur Verfügung. Berechne
den erforderlichen Vorwiderstand.
Station 5 A (Schutzwiderstand) Lösung
(a) Man schaltet vor die Leuchtdiode einen ohmschen Widerstand in Reihe, an
dem die überschüssige Spannung vom Betrag
Ubatt − Udiode
abfällt
(b) Im Fall des Maximalstroms muss am Widerstand die Spannung
UR
abfallen:
UR = Ubatt − Udiode ,
also
UR = 6, 0 V − 1, 5 V = 4, 5 V.
Aus dem Maximalstrom
Imax
R=
und
UR
kann
R
berechnet werden:
UR
4, 5 V
=
= 150 Ω.
Imax
0, 030 A
Man benötigt einen Vorwiderstand von ca.
150 Ω.
Station 5 B (Schutzwiderstand) Lösung
Wenn am Signallämpchen nur
5, 0 V
4, 0 V
anliegen sollen, müssen
9, 0 V − 4, 0 V =
an dem (in Reihe dazu geschalteten) Vorwiderstand anliegen.
Die Gröÿe des Vorwiderstands
UV = 5, 0 V
R
ergibt sich jetzt aus anliegender Spannung
und maximaler Stromstärke
R=
Imax = 0, 10 A:
UV
5, 0 V
=
= 50 Ω.
Imax
0, 10 A
Station 6 A (Mehrere Widerstände)
Drei Widerstände von
50 Ω
a)
sind in unterschiedlicher Weise geschaltet.
b)
c)
Wie groÿ ist der jeweilige Gesamtwiderstand?
Station 6 B (Mehrere Widerstände)
Drei Glühlampen sind wie skizziert verschaltet. Für jede der drei Lampen gelten
die Daten 6,0V/0,30A. Es wird für die Berechnungen die Gültigkeit des ohmschen
Gesetzes angenommen.
(a) Welche Lampen leuchten bei den Schalterstellungen 0, 1, 2 und 3. Gehe auch
auf die Helligkeit der Lampen ein (Relativangabe).
(b) Berechne für die Schalterstellung 3 den Gesamtwiderstand der Schaltung.
(c) Welche Spannung
U2
liegt bei Schalterstellung 3 an der Lampe
terie liefert eine Spannung von
6, 0 V.
L2 ?
Die Bat-
Station 6 A (Mehrere Widerstände) Lösung
(a) Der Gesamtwiderstand ist einfach die Summe der drei Widerstände:
Rges = 50 Ω + 50 Ω + 50 Ω = 150 Ω.
(b) Für die parallel geschalteten Widerstände ergibt sich:
1
Rpar.
und somit
=
1
1
2
1
+
=
=
50 Ω 50 Ω 50 Ω 25 Ω
Rpar. = 25 Ω.
Dieser ist in Reihe mit einem
50 Ω-Widerstand
geschaltet, also
Rges = 50 Ω + 25 Ω = 75 Ω.
(c) Hier sind die Widerstände alle parallel geschaltet, also gilt für den Gesamtwiderstand:
1
1
1
3
1
=
+
+
=
Rges
50 Ω 50 Ω 50 Ω 50 Ω
und somit
Rges =
50 Ω
≈ 16, 7 Ω.
3
Station 6 B (Mehrere Widerstände) Lösung
(a) Man erhält:
Schalter-
L1
L2
L3
stellung
0
Leuchten gleich hell,
jedoch nicht mit voller Helligkeit
1
volle Helligkeit
2
volle Helligkeit
3
leuchtet mit Helligkeit,
leuchten gleich hell, jedoch nicht
die zwischen Stellung 0 und 2 liegt
so hell wie L1 und L2 in Stellung 0
(b) Berechnung des Widerstandes einer Lampe:
RL =
6, 0 V
U
=
= 20 Ω
I
0, 30 A
In Schalterstellung 3 sind L2 und L3 parallel geschaltet und dieses dann in
Reihe zu L1. Für den Widerstand der Parallelschaltung von L2 und L3 gilt:
1
1
1
1
=
+
=
,
R2,3
20 Ω 20 Ω 10 Ω
somit
R2,3 = 10 Ω.
Der Gesamtwiderstand ist dann
Rges = RL + R2,3 = 20 Ω + 10 Ω = 30 Ω.
(c) Da
an
R2,3 ein Drittel des Gesamtwiderstands ausmacht (10 von 30 Ω), liegt auch
1
L2 und L3 ein Drittel der Gesamtspannung an, also
3 · 6, 0 V = 2, 0 V.
Station 7 A (Knobel-Zusatz)
Eine Haushaltsglühlampe
L1
(230 V / 1,0 A) und eine Experimentierlampe
(6,0 V / 5,0 A) werden in Serie an eine Haushaltssteckdose (Unetz
L2
= 230 V) geschal-
tet.
(a) Überlege mit Hilfe einer Rechnung, ob dies die beiden Lampen unbeschädigt
überstehen werden. Starke Vereinfachung: Nimm an, dass sich die Lampen
wie ohmsche Widerstände verhalten (was in der Praxis nicht der Fall ist).
(b) Welcher der beiden Leuchtkörper wird stärker von seiner Normalhelligkeit
(Helligkeit bei Anschluss an die Nennspannung) abweichen?
(c) Nun werden parallel zu den Lampen die Schalter
S1
und
S2
angebracht. Was
kann man über den Leuchtzustand der Lampen sagen, wenn
• S1
• S1
geschlossen und
oen und
S2
S2
oen ist?
geschlossen ist?
Station 7 B (Knobel-Zusatz)
Der gezeigte Stromkreis enthält zwei baugleiche Glühlampen A und B und drei baugleiche ohmsche Widerstände R. Die Batterie liefert während der folgenden Veränderungen eine konstante Spannung. Die Antworten sind sorgfältig zu begründen.
(a) Vergleiche die Helligkeiten der Lampen A und B.
(b) Was passiert mit der Helligkeit der Lampe B, wenn A
1. herausgeschraubt,
2. überbrückt wird?
(c) A wird wieder eingebaut, und nun B erst herausgeschraubt und dann überbrückt. Was passiert in beiden Fällen mit der Helligkeit von A?
(d) Nun sind alle Lampen wieder am Platz und ein Kabel schlieÿt die Punkte 1
und 3 kurz.
1. Was passiert mit der Helligkeit der Lampen?
2. Wie ändert sich die Spannung zwischen den Punkten 3 und 2?
(e) Gehe wieder vom Ausgangsbild aus und untersuche ähnlich wie in Teilaufgabe
d) die Auswirkung einer Verbindung
1. der Punkte 2 und 4 auf die Helligkeiten und die Spannung (zwischen Punkt
1 und 4),
2. der Punkte 3 und 4 auf die Helligkeiten und die Spannung (zwischen Punkt
2 und 3 und zwischen Punkt 1 und 3).
Station 7 A (Knobel-Zusatz) Lösung
(a) Für die Widerstände der Lampen gilt:
RL1 =
230 V
= 230 Ω
1, 0 A
RL2 =
6, 0 V
= 1, 2 Ω.
5, 0 A
und
Lampe
L2
bei
L1
allein übersteht den Anschluss an das Haushaltsnetz unbeschadet,
wäre dies nicht der Fall. Wenn beide Lampen in Serie geschaltet wer-
den, erhöht sich der Gesamtwiderstand, der Strom wird also geringfügig unter
1, 0 A
liegen. Beide Lampen bleiben bei dieser Stromstärke funktionsfähig.
(b) Für den Strom durch die Serienschaltung gilt:
I1,2 =
230 V
230 V
Unetz
=
=
≈ 0, 99 A.
RL1 + RL2
230 Ω + 1, 2 Ω 231, 2 Ω
Diese Stromstärke weicht nur geringfügig von der Nennstromstärke der Lampe
(c)
L1
ab. Diese Lampe wird also nahezu mit ihrer Normalhelligkeit leuchten.
L2
Lampe L2
I1,2
Bei Lampe
liegt
Die
wird also nur schwach leuchten.
•
mehr als einen Faktor 5 unter der Nennstromstärke.
S1 geschlossen und S2 oen:
Die Lampe
L1
ist kurzgeschlossen, der gesamte Strom ieÿt über S1. In
diesem Fall bleibt L1 dunkel. Die gesamte Netzspannung liegt an
Da die Nennspannung dieser Lampe nur
L2
an.
6, 0 V ist, wird sie wohl zerstört
werden.
•
S1 oen und S2 geschlossen:
Die Lampe
L2
ist kurzgeschlossen, der gesamte Strom ieÿt über S2.
Die gesamte Netzspannung liegt an
L1
an. Da die Nennspannung dieser
Lampe 230 V ist, wird sie in normaler Helligkeit leuchten, während
dunkel bleibt.
L2
Station 7 B (Knobel-Zusatz) Lösung
(a) A ist heller als B, da der Strom in der Hauptleitung gröÿer ist als in den
Teilzweigen.
(b)
•
Wird A herausgeschraubt, so verlöschen beide Lampen, da kein Strom
mehr ieÿen kann.
•
Wird A überbrückt, so sinkt der Gesamtwiderstand. Der Strom in der
Hauptleitung und in den Teilzweigen wird dadurch gröÿer und die Lampe B leuchtet somit heller.
(c)
•
Wird B herausgeschraubt, so steigt der Gesamtwiderstand der Schaltung, da der noch bestehende obere Teilzweig einen höheren Widerstand
hat als die Parallelschaltung. Die Lampe A wird dunkler.
•
Wird B überbrückt, so sinkt der Widerstand des unteren Teilzweiges
und somit auch der Widerstand der Parallelschaltung. Der Gesamtwiderstand wird kleiner, die Lampe A leuchtet heller.
(d) Nun sind alle Lampen wieder am Platz und ein Kabel schlieÿt die Punkte 1
und 3 kurz.
•
Durch die Überbrückung verlischt die Lampe A. Der Gesamtwiderstand
der Schaltung wird kleiner und somit der Strom in der Haupt- und in
den Nebenleitungen gröÿer. Somit leuchtet B heller.
•
Während vor der Überbrückung eine Spannungsteilerschaltung von Lampe A und R1 einerseits und der Parallelschaltung andererseits vorlag, an
der die Batteriespannung lag, liegt nun die gesamte Batteriespannung
nur noch an der Parallelschaltung. Also steigt die Spannung zwischen 3
und 2.
(e) Gehe wieder vom Ausgangsbild aus und untersuche ähnlich wie in Teilaufgabe
d) die Auswirkung einer Verbindung
a) der Punkte 2 und 4 auf die Helligkeiten und die Spannung (zwischen
Punkt 1 und 4),
Durch die Verbindung von 2 und 4 ändert sich weder in der Helligkeit
der Lampen noch in den Spannungen etwas, da die Punkte 2 und 4
sowieso schon verbunden sind.
b) der Punkte 3 und 4 auf die Helligkeiten und die Spannung (zwischen
Punkt 2 und 3 und zwischen Punkt 1 und 3).
Durch diese Maÿnahme wird der obere Teilzweig kurzgeschlossen. Dadurch erlöscht Lampe B. Da der Widerstand der Gesamtschaltung sinkt,
wird A heller. Die Spannung zwischen den Punkten 2 und 3 ist Null, da
2 mit 3 kurzgeschlossen ist. Somit liegt die gesamte Batteriespannung
zwischen den Punkten 1 und 3.