Parallelschaltung von Widerständen I U RR RR R + ⋅ = Ohm Ohm
Werbung
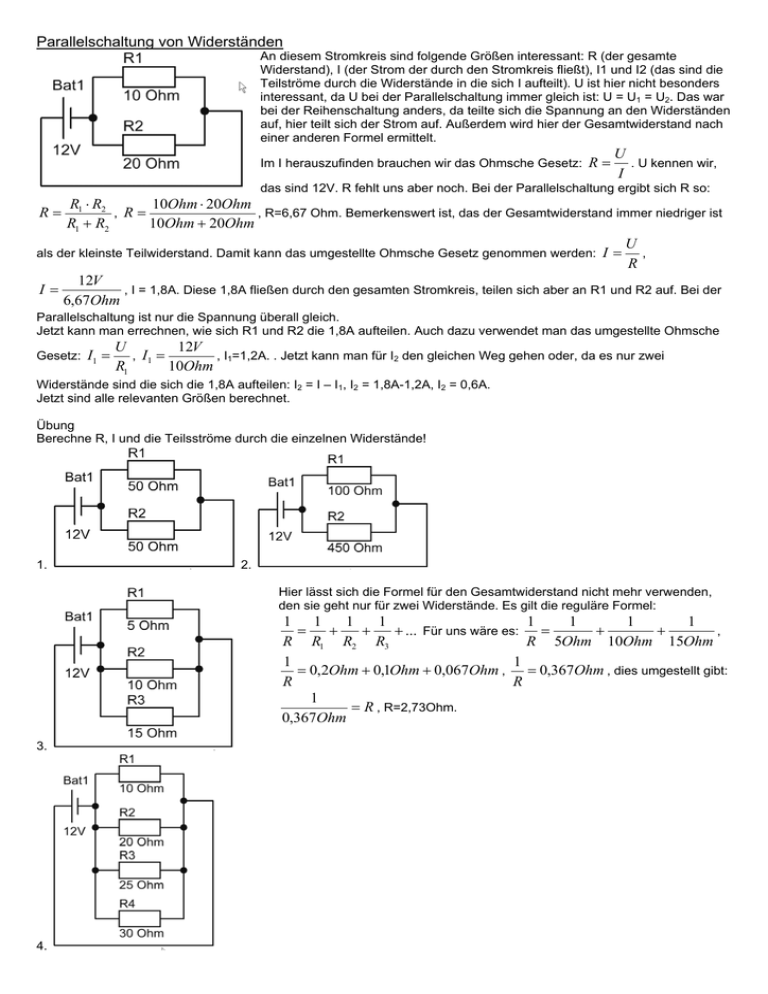
Parallelschaltung von Widerständen An diesem Stromkreis sind folgende Größen interessant: R (der gesamte Widerstand), I (der Strom der durch den Stromkreis fließt), I1 und I2 (das sind die Teilströme durch die Widerstände in die sich I aufteilt). U ist hier nicht besonders interessant, da U bei der Parallelschaltung immer gleich ist: U = U1 = U2. Das war bei der Reihenschaltung anders, da teilte sich die Spannung an den Widerständen auf, hier teilt sich der Strom auf. Außerdem wird hier der Gesamtwiderstand nach einer anderen Formel ermittelt. Im I herauszufinden brauchen wir das Ohmsche Gesetz: R = U . U kennen wir, I das sind 12V. R fehlt uns aber noch. Bei der Parallelschaltung ergibt sich R so: R1 ⋅ R2 10Ohm ⋅ 20Ohm , R= , R=6,67 Ohm. Bemerkenswert ist, das der Gesamtwiderstand immer niedriger ist R1 + R2 10Ohm + 20Ohm U als der kleinste Teilwiderstand. Damit kann das umgestellte Ohmsche Gesetz genommen werden: I = , R 12V I= , I = 1,8A. Diese 1,8A fließen durch den gesamten Stromkreis, teilen sich aber an R1 und R2 auf. Bei der 6,67Ohm R= Parallelschaltung ist nur die Spannung überall gleich. Jetzt kann man errechnen, wie sich R1 und R2 die 1,8A aufteilen. Auch dazu verwendet man das umgestellte Ohmsche Gesetz: I1 = U 12V , I1 = , I1=1,2A. . Jetzt kann man für I2 den gleichen Weg gehen oder, da es nur zwei R1 10Ohm Widerstände sind die sich die 1,8A aufteilen: I2 = I – I1, I2 = 1,8A-1,2A, I2 = 0,6A. Jetzt sind alle relevanten Größen berechnet. Übung Berechne R, I und die Teilsströme durch die einzelnen Widerstände! 1. 2. Hier lässt sich die Formel für den Gesamtwiderstand nicht mehr verwenden, den sie geht nur für zwei Widerstände. Es gilt die reguläre Formel: 1 1 1 1 1 1 1 1 = + + + ... Für uns wäre es: = + + , R R1 R2 R3 R 5Ohm 10Ohm 15Ohm 1 1 = 0,2Ohm + 0,1Ohm + 0,067Ohm , = 0,367Ohm , dies umgestellt gibt: R R 1 = R , R=2,73Ohm. 0,367Ohm 3. 4.