3 Vierecke und Vielecke

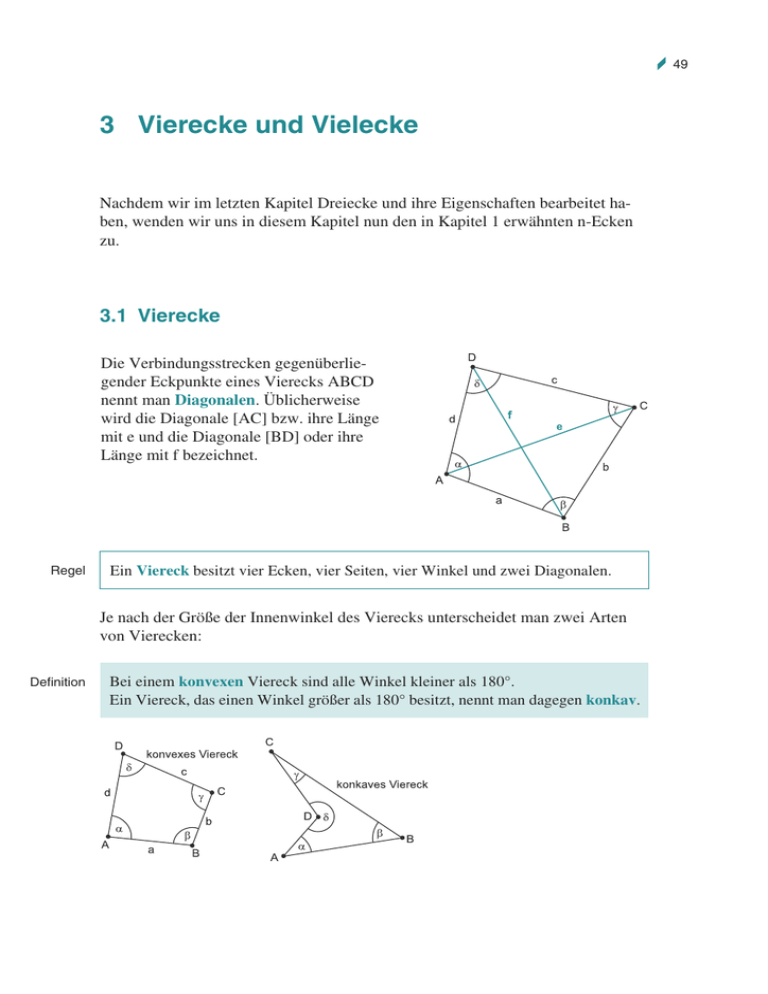
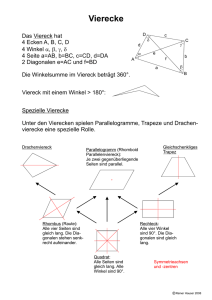
r 49
3 Vierecke und Vielecke
Nachdem wir im letzten Kapitel Dreiecke und ihre Eigenschaften bearbeitet haben, wenden wir uns in diesem Kapitel nun den in Kapitel 1 erwähnten n-Ecken
zu.
3.1 Vierecke
Die Verbindungsstrecken gegenüberliegender Eckpunkte eines Vierecks ABCD
nennt man Diagonalen. Üblicherweise
wird die Diagonale [AC] bzw. ihre Länge
mit e und die Diagonale [BD] oder ihre
Länge mit f bezeichnet.
Regel
Ein Viereck besitzt vier Ecken, vier Seiten, vier Winkel und zwei Diagonalen.
Je nach der Größe der Innenwinkel des Vierecks unterscheidet man zwei Arten
von Vierecken:
Definition
Bei einem konvexen Viereck sind alle Winkel kleiner als 180°.
Ein Viereck, das einen Winkel größer als 180° besitzt, nennt man dagegen konkav.
50 r Vierecke und Vielecke
Im Folgenden werden wir nur die konvexen Vierecke näher betrachten. Bei konvexen Vierecken liegen die Diagonalen im Innern des Vierecks. Je nach der Größe der Winkel sowie der Länge der Seiten unterscheidet man verschiedene Vierecke (die schwarzen Geraden sind Symmetrieachsen des jeweiligen Vierecks):
Allgemeines Viereck
Jedes Viereck ist ein allgemeines Viereck. Wenn ein Viereck besondere Eigenschaften wie z. B. gleich lange Seiten aufweist, dann gibt man diesem Viereck
noch besondere Namen, die nachfolgend beschrieben sind.