vierseitig

3. Inferenz in der Logik
Allgemeines zu Wissensverarbeitung und Inferenz
3. Inferenz in der Logik
Allgemeines zu Wissensverarbeitung und Inferenz
3. Inferenz in Aussagen- und Prädikatenlogik
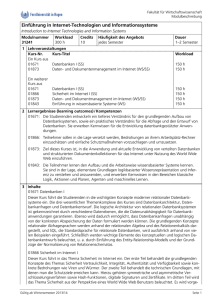
Auswirkungen von
1 Euro = 0.96 Dollar
auf Zinsen und
Aktienkurse
Devisenkurs
1 Euro = 0.96 Dollar
Wissen, Kennen, Können
Umgangssprachlich bezeichnet man das Ergebnis eines Lernvorgangs als
Wissen
• wissen, wenn es sich um sprachlich-begriffliche Fähigkeiten handelt,
• kennen, wenn es sich um sinnliche Wahrnehmung handelt,
• können, wenn es sich um motorische Fähigkeiten handelt.
Ergebnis
eines
Lernvorgangs
Information
Kontext
0.96
Daten
Peter Becker, Wissensbasierte Systeme I — FH Bonn-Rhein-Sieg, SS 04
3. Inferenz in der Logik
102
Allgemeines zu Wissensverarbeitung und Inferenz
Peter Becker, Wissensbasierte Systeme I — FH Bonn-Rhein-Sieg, SS 04
3. Inferenz in der Logik
104
Allgemeines zu Wissensverarbeitung und Inferenz
Wissen: Versuche einer Definition
Arten von Wissen
explizit
implizit
• Knowledge is organized information applicable to problem solving. (Woolf)
• Knowledge is information that has been organized and analyzed to make it understandable and applicable to problem solving or decision making. (Turban)
Ableitung
präzise
unsicher
Wissen
Art
unvollständig
vage
Repräsentation
Kontollstrategie
Peter Becker, Wissensbasierte Systeme I — FH Bonn-Rhein-Sieg, SS 04
103
Regeln
Fakten
Peter Becker, Wissensbasierte Systeme I — FH Bonn-Rhein-Sieg, SS 04
105
3. Inferenz in der Logik
Allgemeines zu Wissensverarbeitung und Inferenz
3. Inferenz in der Logik
Wissensebenen
Repräsentation von Wissen
• kognitive Ebene (z.B. Erfahrung von Experten, Arbeitsanweisungen)
• Repräsentationsebene (z.B. Aussagenlogik, Prädikatenlogik)
• Implementierungsebene (z.B. Prolog-Statements)
☞ Bei der Wissensverarbeitung und der Künstlichen Intelligenz stehen die Repr äsentationsebene und die Implementierungsebene im Vordergrund (Schließen der KILücke).
☞ Beim Wissensmanagement stehen die kognitive Ebene und die Repr äsentationsebene im Vordergrund.
Peter Becker, Wissensbasierte Systeme I — FH Bonn-Rhein-Sieg, SS 04
3. Inferenz in der Logik
106
Allgemeines zu Wissensverarbeitung und Inferenz
Daten- vs. Wissensverarbeitung
Algorithmische Problembeschreibung
Daten
Software−
Entwickler
Programm
• In einem Sortierprogramm ist das Wissen um die Eigenschaften von Ordnungen
und sortierten Listen implizit im Algorithmus dargestellt.
☞ prozedurales Wissen
• Das Wissen, das in konventionellen Programmen in Form von Daten, Tabellen oder
Datenbanken ausgedrückt ist, ist auf explizite Art repr äsentiert.
☞ deklaratives Wissen
Bei wissensbasierten Systemen liegt der Schwerpunkt auf deklarativem Wissen.
Peter Becker, Wissensbasierte Systeme I — FH Bonn-Rhein-Sieg, SS 04
3. Inferenz in der Logik
108
Allgemeines zu Wissensverarbeitung und Inferenz
Kriterien für die Wissensrepräsentation:
Anwendungsspezifisches Wissen
Wissen
(Fakten
und
Regeln)
Allgemeines zu Wissensverarbeitung und Inferenz
•
•
•
•
•
•
Vollständigkeit
Abstraktion
Ökonomie
Freiheit von Redundanz
Widerspruchsfreihet
Transparenz
Wissens−
ingenieur
Inferenz−
maschine
Peter Becker, Wissensbasierte Systeme I — FH Bonn-Rhein-Sieg, SS 04
107
Peter Becker, Wissensbasierte Systeme I — FH Bonn-Rhein-Sieg, SS 04
109
3. Inferenz in der Logik
Inferenz
3. Inferenz in der Logik
Inferenz
Logik und Inferenz
• Nehmen wir an, es gibt eine Menge von Regeln, wie sich ein Autofahrer im Straßenverkehr zu verhalten hat.
• Die Regeln sind beispielsweise in “wenn...dann”-Form repräsentiert.
• Weiterhin gebe es Fakten, die Tatsachen widerspiegeln (Geschwindigkeit, Geschwindigkeitsbegrenzung, Ampel, etc.).
• Regeln und Fakten bilden die Wissensbasis.
• In solch einer Wissensbasis gibt es keine Kontrollstrukturen wie in einem
herkömmlichen Programm, die festlegen, in welcher Reihenfolge die Regeln anzuwenden sind.
• Stattdessen muß ein Mechanismus vorhanden sein, der bestimmt, welche Regeln
wie anzuwenden sind.
• Dieser Mechanismus heißt Inferenzmechanismus.
• Inferenz ist ein (Denk-)Prozeß, in dem aus vorhandenem Wissen (bzw. Annahmen
oder Vermutungen) neues Wissen (Annahmen, Vermutungen) gewonnen werden.
Peter Becker, Wissensbasierte Systeme I — FH Bonn-Rhein-Sieg, SS 04
3. Inferenz in der Logik
110
Inferenz
• Neues Wissen heißt hier, daß nach Inferenz etwas verfügbar ist, was vorher nicht
unmittelbar verfügbar war.
• Wissensbasis: Wenn es regnet, dann ist die Straße naß. Es regnet.
Inferenz (mit Modus Ponens): Die Straße ist naß.
Peter Becker, Wissensbasierte Systeme I — FH Bonn-Rhein-Sieg, SS 04
Inferenz
111
Gegenstand der Logik:
• Repräsentation von Wissen durch Formeln einer adäquaten Logiksprache
– Syntax der Logiksprache
– Bedeutung (Interpretation) von Formeln der Logiksprache
• Herleitung (Inferenz) von neuem Wissen auf Basis der Kalküls.
– Definition des Folgerungsbegriffs
– Übertragung der semantischen Folgerung auf äquivalente syntaktische Umformungen
Peter Becker, Wissensbasierte Systeme I — FH Bonn-Rhein-Sieg, SS 04
3. Inferenz in der Logik
112
Inferenz
Anwendungsgebiete der Logik in der Wissensverarbeitung:
•
•
•
•
Inferenz in Expertensystemen
Logikprogrammierung, deduktive Datenbanken
automatisches Beweisen
Programmverifikation
Peter Becker, Wissensbasierte Systeme I — FH Bonn-Rhein-Sieg, SS 04
113
3. Inferenz in der Logik
Inferenz
3. Inferenz in der Logik
Zielrichtungen der Inferenz
Weitere Aspekte bei der Wissensverarbeitung mit Logik
• Prognosen, logische Ableitungen erstellen
Es sind Fakten F und Regeln R gegeben. Was kann daraus gefolgert werden?
Beispiel: Wenn es regnet, dann ist die Straße naß. Was kann aus der Tatsache,
daß es regnet, gefolgert werden?
• Erklärungen finden
Wie läßt sich ein Fakt F mit Hilfe der Regeln R erklären?
Beispiel: Die Straße ist naß. Wie kann das sein?
• Hypothesen prüfen
Können aus den Fakten F und den Regeln R die Hypothesen H hergeleitet werden?
Beipiel: Wenn es regnet, dann ist die Straße naß. Es regnet. Ist die Straße dann
naß?
Peter Becker, Wissensbasierte Systeme I — FH Bonn-Rhein-Sieg, SS 04
3. Inferenz in der Logik
114
Inferenz
Arten der Inferenz
•
•
•
•
Qualifikationsproblem
unpräzise Angaben
probabilistische Aussagen und Regeln
räumlich-zeitliches Wissen
Peter Becker, Wissensbasierte Systeme I — FH Bonn-Rhein-Sieg, SS 04
3. Inferenz in der Logik
116
Aussagenlogik
Signatur
• Deduktion
Zum Starten eines Autos ist eine aufgeladene Batterie notwendig. Bei unserem
Auto ist die Batterie leer. Wir schließen, daß wir unser Auto nicht starten k önnen.
• Induktion
Wir haben wiederholt beobachtet, daß ein Auto nicht startet und die Batterie leer
ist. Wir haben noch nie beobachtet, daß ein Auto mit leerer Batterie gestartet werden konnte. Wir schließen daraus, daß ein Auto, das eine leere Batterie hat, nicht
gestartet werden kann.
• Abduktion
Zum Starten eines Autos ist eine aufgeladene Batterie notwendig. Unser Auto l äßt
sich nicht starten. Wir schließen, daß die Batterie leer ist.
Peter Becker, Wissensbasierte Systeme I — FH Bonn-Rhein-Sieg, SS 04
Inferenz
115
Am Beispiel der Aussagenlogik erklären wir schrittweise wichtige Elemente eines logischen Systems.
• Zunächst benötigt ein logisches System ein Vokabular,
• d.h. eine Menge von Namen, die Dinge der realen Welt beschreiben k önnen.
• Eine derartige Menge von Namen wird als Signatur bezeichnet und üblicherweise
durch Σ gekennzeichnet.
• Den Namen ist i.d.R. eine gewisse Stelligkeit zugeordnet.
Peter Becker, Wissensbasierte Systeme I — FH Bonn-Rhein-Sieg, SS 04
117
3. Inferenz in der Logik
Aussagenlogik
3. Inferenz in der Logik
Aussagenlogik
Aussagenlogische Signatur
Aussagenlogische Formeln
Definition 3.1. Eine aussagenlogische Signatur Σ ist eine Menge von (nullstelligen)
Bezeichnern, den Aussagenvariablen.
Definition 3.2. Für eine aussagenlogische Signatur Σ ist die Menge Formel(Σ) der
aussagenlogischen Formeln wie folgt definiert:
Beispiel 3.1. Die Menge
• Die Elemente der Menge Σ sind aussagenlogische Formeln, die sogenannten atomaren Formeln.
• Falls F und G aussagenlogische Formeln sind, dann sind auch die folgenden Konstrukte aussagenlogische Formeln:
ΣAL := {hatFieber, istKrank, istArbeitsunfähig}
ist eine aussagenlogische Signatur, die drei Aussagenvariablen zur Verfügung stellt.
Im folgenden benutzen wir üblicherweise Großbuchstaben als Aussagenvariablen.
Peter Becker, Wissensbasierte Systeme I — FH Bonn-Rhein-Sieg, SS 04
3. Inferenz in der Logik
118
Aussagenlogik
Peter Becker, Wissensbasierte Systeme I — FH Bonn-Rhein-Sieg, SS 04
3. Inferenz in der Logik
120
Aussagenlogik
Formeln
•
•
•
•
•
•
(¬F )
(F ∧ G)
(F ∨ G)
(F → G)
(F ↔ G)
Formeln ermöglichen es, Dinge der repräsentierten Welt auszudrücken.
Formeln entsprechen einer gewissen Syntax (sie sind wohlgeformt).
Diese Syntax legt eine Wissensrepräsentationssprache fest.
Formeln sind üblicherweise rekursiv aufgebaut.
Die atomaren Formeln ergeben sich aus der Signatur.
Mit logischen Verknüpfungsoperatoren (den Junktoren) werden aus atomaren Formeln schrittweise komplexere Formeln aufgebaut.
Peter Becker, Wissensbasierte Systeme I — FH Bonn-Rhein-Sieg, SS 04
119
Negation
Konjunktion
Disjunktion
Implikation
Äquivalenz
Bemerkung 3.1. Zur Vereinfachung der Schreibweise verzichten wir i.d.R. auf
die Klammerung und benutzen statt dessen die folgenden Bindungspriorit äten:
¬, ∧, ∨, →, ↔.
Durch die Menge Formel(Σ) wird die Sprache zur Repräsentation von Wissen definiert.
Peter Becker, Wissensbasierte Systeme I — FH Bonn-Rhein-Sieg, SS 04
121
3. Inferenz in der Logik
Aussagenlogik
3. Inferenz in der Logik
Σ-Interpretation
Aussagenlogik
Erfüllungsrelation
• Die Syntax einer Logik legt ausschließlich deren äußere Form fest, sie sagt aber
nichts über die Bedeutung der Formeln aus.
• Benötigt wird eine Verbindung zwischen den syntaktischen Elementen der Logik
und den Objekten der zu repräsentierenden Welt.
• Diese Verbindung wird durch eine sogenannte Σ-Interpretation hergestellt.
• Eine Σ-Interpretation einer Signatur ist die Zuordnung von den Elementen der Signatur Σ (Namen) zu den Elementen der zu repräsentierenden Welt.
• Die Interpretation liefert uns nur einen Wahrheitswert für die atomaren Formeln.
• Wir benötigen eine Ausdehnung der Semantik auf alle Formeln F ∈ Formel(Σ).
• Dieses stellt uns eine Erfüllungsrelation |= bereit.
• Durch solch eine Erfüllungsrelation ist definiert, ob eine Formel F in einer ΣInterpretation I wahr ist oder nicht, d.h.
• sie ordnet einer Interpretation und einer Formel einen Wahrheitswert zu.
• Eine Erfüllungsrelation definiert hierzu im wesentlichen die Semantik der Junktoren.
Definition 3.4. Es seien F, G ∈ Formel(Σ) (nichtatomare) aussagenlogische Formeln. Durch die folgenden Wahrheitstafel wird eine Σ-Interpretation I von Σ auf die
Peter Becker, Wissensbasierte Systeme I — FH Bonn-Rhein-Sieg, SS 04
122
3. Inferenz in der Logik
Aussagenlogik
Belegung
124
3. Inferenz in der Logik
Aussagenlogik
Menge Formel(Σ) ausgedehnt:
I(F )
f
w
Definition 3.3. Es sei Σ eine aussagenlogische Signatur.
• Eine Abbildung I : Σ −→ {wahr, falsch} heißt aussagenlogische Interpretation
oder Belegung für Σ.
• Int(Σ) bezeichnet die Menge der Belegungen für Σ.
Beispiel 3.2. Für die Signatur aus Beispiel 3.1 ist I definiert durch
I(hatFieber)
I(istKrank)
I(istArbeitsunfähig)
Peter Becker, Wissensbasierte Systeme I — FH Bonn-Rhein-Sieg, SS 04
=
=
=
wahr
wahr
falsch
I(¬F )
w
f
I(F ) I(G) I(F ∨ G) I(F ∧ G)
f
f
f
f
w
f
f
w
w
f
w
f
w
w
w
w
Für I ∈ Int(Σ) und F ∈ Formel(Σ) gelte:
I(F → G)
w
w
f
w
I |= F gdw. I(F ) = wahr
eine mögliche Belegung.
Peter Becker, Wissensbasierte Systeme I — FH Bonn-Rhein-Sieg, SS 04
123
Peter Becker, Wissensbasierte Systeme I — FH Bonn-Rhein-Sieg, SS 04
125
3. Inferenz in der Logik
Aussagenlogik
3. Inferenz in der Logik
Aussagenlogik
Modell
Erfüllbarkeit
Definition 3.5. Es seien I ∈ Int(Σ) und F ∈ Formel(Σ). Gilt I |= F , so sagen wir
Besonders interessant sind Formeln, die für alle Interpretationen wahr bzw. falsch
sind.
• “I erfüllt F ” und
• bezeichnen I als Σ-Modell für F .
“Kräht der Hahn auf dem Mist, ändert sich das Wetter oder es bleibt wie es ist.”
Definition 3.6. Eine Formel F heißt
ModΣ (F ) ⊆ Int(Σ) bezeichnet die Menge aller Σ-Modelle für F .
Für eine Menge F ⊂ Formel(Σ) von Formeln gelte I |= F gdw. I |= F für alle
F ∈ F . I ist dann ein Modell für die Formelmenge F .
•
•
•
•
erfüllbar gdw. es ein Modell für die Formel gibt.
unerfüllbar (Kontradiktion) gdw. es kein Modell für die Formel gibt.
allgemeingültig (Tautologie) gdw. jede Interpretation ein Modell für die Formel ist.
falsifizierbar gdw. es eine Interpretation gibt, die kein Modell für die Formel ist.
Die Begriffe werden in analoger Weise für Formelmengen F ⊂ Formel(Σ) verwendet.
Peter Becker, Wissensbasierte Systeme I — FH Bonn-Rhein-Sieg, SS 04
3. Inferenz in der Logik
126
Aussagenlogik
Beispiel 3.3. Die Interpretation I aus Beispiel 3.2 ist ein Modell für die Formel
Peter Becker, Wissensbasierte Systeme I — FH Bonn-Rhein-Sieg, SS 04
3. Inferenz in der Logik
128
Aussagenlogik
Beispiel 3.4. Wichtige Tautologien sind:
hatFieber → istKrank
• Modus Ponens
(F ∧ (F → G)) → G
Dagegen ist I kein Modell für die Formel
• Modus Tollens
((F → G) ∧ ¬G) → ¬F
istKrank → istArbeitsunfähig
• Und-Elimination
Beweis mit Wahrheitstafeln ✎.
(F ∧ G) → F
• Oder-Introduktion
F → (F ∨ G)
• Resolutionsregel
((F → G) ∧ (¬F → H)) → (G ∨ H)
Peter Becker, Wissensbasierte Systeme I — FH Bonn-Rhein-Sieg, SS 04
127
Peter Becker, Wissensbasierte Systeme I — FH Bonn-Rhein-Sieg, SS 04
129
3. Inferenz in der Logik
Aussagenlogik
3. Inferenz in der Logik
Aussagenlogik
Semantische Folgerung
Beispiel 3.6. Wir wollen uns ein Haustier anschaffen und machen folgende Überlegungen:
• In einem wissensbasierten System wollen wir Fakten aus anderen Fakten und Regeln herleiten.
2. Besitzer wertvoller Möbel (W ) sollten keine Katze anschaffen, da diese die Möbel
zerkratzen würde.
• Wir können eine Wissensbasis als eine Menge F ⊂ Formel(Σ) betrachten.
3. Ein Hund erfordert ein freistehendes Haus (F ), damit sich kein Nachbar durch das
Bellen gestört fühlt.
1. Es sollte nur ein Hund (H ), eine Katze (K ) oder ein Hamster (M ) sein.
• Eine solche Menge F = {F1 , . . . , Fn} entspricht der Konjunktion F1 ∧ . . . ∧ Fn.
• Unser übliches Verständnis von Folgerung läßt sich so ausdrücken: Ist eine Formel
G immer dann wahr, wenn alle Formeln aus F wahr sind, dann folgt G aus F .
• Damit können wir die Erfüllungsrelation |= auf eine Beziehung zwischen Formeln
und Formelmengen ausdehnen.
Wir vermuten: Für einen Besitzer wertvoller Möbel ohne freistehendes Haus kommt
nur ein Hamster in Frage.
Die Aussagen lauten als Aussagenlogische Formeln:
Definition 3.7. Es seien F, G ∈ Formel(Σ) aussagenlogische Formeln.
1. H ∨ K ∨ M
• G heißt semantische Folgerung von F gdw. jedes Modell für F auch ein Modell für
G ist.
Peter Becker, Wissensbasierte Systeme I — FH Bonn-Rhein-Sieg, SS 04
3. Inferenz in der Logik
130
Aussagenlogik
• In diesem Fall schreiben wir F |= G.
• Wir sagen auch “G folgt logisch aus F ” bzw. “aus F folgt semantisch G”.
• Für eine Formelmenge F gelte F |= G gdw. jedes Modell für F auch ein Modell
für G ist.
• Für Formelmengen F , G gelte F |= G gdw. F |= G für alle G ∈ G gilt.
Beispiel 3.5. Gegeben sei die Formelmenge F
8
< hatFieber
F =
istKrank
:
hatFieber
→
→
9
istKrank,
=
istArbeitsunfähig,
;
2. W → ¬K
3. H → F
Peter Becker, Wissensbasierte Systeme I — FH Bonn-Rhein-Sieg, SS 04
132
3. Inferenz in der Logik
Aussagenlogik
Hyp. W ∧ ¬F → M ∧ ¬H ∧ ¬K
N r.
1.
2.
3.
4.
5.
6.
I(H)
f
f
f
f
f
f
I(K)
f
f
f
f
f
f
I(M )
f
f
f
f
w
w
I(W )
f
f
w
w
f
f
I(F )
f
w
f
w
f
w
1. ∧ 2. ∧ 3.
f
f
f
f
f
f
Hyp.
w
w
f
w
w
w
Kann aus F die Aussage istArbeitsunfähig gefolgert werden, d.h. gilt F |=
istArbeitsunfähig?
Ja! Beweis mit Wahrheitstafeln ✎.
Peter Becker, Wissensbasierte Systeme I — FH Bonn-Rhein-Sieg, SS 04
131
Peter Becker, Wissensbasierte Systeme I — FH Bonn-Rhein-Sieg, SS 04
133
3. Inferenz in der Logik
Aussagenlogik
3. Inferenz in der Logik
Aussagenlogik
Fazit:
N r.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
I(H)
f
f
f
f
f
f
f
f
f
f
w
w
w
I(K)
f
f
w
w
w
w
w
w
w
w
f
f
f
I(M )
w
w
f
f
f
f
w
w
w
w
f
f
f
I(W )
w
w
f
f
w
w
f
f
w
w
f
f
w
I(F )
f
w
f
w
f
w
f
w
f
w
f
w
f
1. ∧ 2. ∧ 3.
w
w
w
f
f
f
w
w
f
f
f
f
f
Hyp.
w
w
w
w
f
w
w
w
f
w
w
w
f
Peter Becker, Wissensbasierte Systeme I — FH Bonn-Rhein-Sieg, SS 04
• Es gibt acht Modelle für die Formelmenge {1., 2., 3.}. Dies sind die Interpretationen mit den Nummern 7, 8, 9, 13, 14, 20, 24, 26.
• Jedes dieser Modelle ist auch ein Modell für die Hypothese.
• Somit folgt die Hypothese semantisch aus {1., 2., 3.}.
134
3. Inferenz in der Logik
Aussagenlogik
Peter Becker, Wissensbasierte Systeme I — FH Bonn-Rhein-Sieg, SS 04
3. Inferenz in der Logik
136
Aussagenlogik
Satz 3.1. Es seien F, G aussagenlogische Formeln. Dann gilt:
N r.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
I(H)
w
w
w
w
w
w
w
w
w
w
w
w
w
I(K)
f
f
f
f
f
w
w
w
w
w
w
w
w
I(M )
f
w
w
w
w
f
f
f
f
w
w
w
w
I(W )
w
f
f
w
w
f
f
w
w
f
f
w
w
I(F )
w
f
w
f
w
f
w
f
w
f
w
f
w
Peter Becker, Wissensbasierte Systeme I — FH Bonn-Rhein-Sieg, SS 04
1. ∧ 2. ∧ 3.
w
f
f
f
w
f
w
f
f
f
f
f
f
Hyp.
w
w
w
f
w
w
w
f
w
w
w
f
w
• F ist Tautologie gdw. ¬F ist unerfüllbar.
• F |= G gdw. F → G ist Tautologie.
• F |= G gdw. F ∧ ¬G ist unerfüllbar.
Bemerkung 3.2. Die Äquivalenzen können auf Formelmengen F , G ausgedehnt
werden.
135
Peter Becker, Wissensbasierte Systeme I — FH Bonn-Rhein-Sieg, SS 04
137
3. Inferenz in der Logik
Aussagenlogik
3. Inferenz in der Logik
Aussagenlogik
Beispiel 3.7. Gegeben sei die Formelmenge F aus Beispiel 3.5. Mit der Inferenzregel Modus Ponens leiten wir ab:
Kalkül
• Schon das kleine Beispiel 3.6 verdeutlichte, daß Inferenz auf Basis der Definition
der semantischen Folgerung ineffizient ist.
• Allgemein müssen für eine Formelmenge F mit k verschiedenen Aussagevariablen 2k Belegungen getestet werden.
• Daher benutzt man für die maschinelle Inferenz Techniken, die allein auf der Syntax
der Formeln beruhen.
• Statt alle möglichen Belegungen zu testen, sucht man nach einer Folge von syntaktischen Umformungen, die die Hypothese zu beweisen.
hatFieber, hatFieber → istKrank
istKrank
Nochmals angewandt ergibt sich:
istKrank, istKrank → istArbeitsunfaehig
istArbeitsunfaehig
Also gilt: F ` istArbeitsunfähig.
• Ein Kalkül besteht aus einer Menge von logischen Axiomen und Inferenzregeln.
• Die Axiome sind entweder eine Menge von elementaren Tautologien (positiver
Kalkül) oder
• eine Menge von elementaren Widersprüchen (negativer Kalkül).
Peter Becker, Wissensbasierte Systeme I — FH Bonn-Rhein-Sieg, SS 04
3. Inferenz in der Logik
138
Aussagenlogik
• Die Inferenzregeln sind Vorschriften, nach denen aus Formeln andere Formeln
abgeleitet werden können.
• Sie werden in der folgenden Form notiert:
F1 , . . . , F n
F
Peter Becker, Wissensbasierte Systeme I — FH Bonn-Rhein-Sieg, SS 04
3. Inferenz in der Logik
140
Aussagenlogik
Eigenschaften von Kalkülen
• Ein Kalkül ist korrekt gdw. alle syntaktischen Ableitungen auch semantische Folgerungen sind, d.h. für Formeln F und G gilt:
F ` G impliziert F |= G
Dies besagt, daß aus den Formeln (der syntaktischen Form) F 1, . . . , Fn (Bedingungen) eine Formel der Form F (Schlussfolgerung) abgeleitet werden kann.
• So können aus den Tautologien von Beispiel 3.4 Inferenzregeln gebildet werden.
Aus dem Modus Ponens ergibt sich die Inferenzregel:
F, F → G
G
• Ein Kalkül ist vollständig gdw. alle semantischen Folgerungen auch syntaktisch
abgeleitet werden können, d.h. für Formeln F und G gilt:
F |= G impliziert F ` G
• Ein Kalkül ist widerlegungsvollständig gdw. aus allen semantischen Folgerungen
eine unerfüllbare Formel 2 abgeleitet werden kann, d.h. für Formeln F und G gilt:
• Ist eine Formel F aus den Formeln F1, . . . , Fn durch eine Folge von Anwendungen der Inferenzregeln ableitbar, so schreibt man
F |= G impliziert F ∧ ¬G ` 2
F1 , . . . , F n ` F
Peter Becker, Wissensbasierte Systeme I — FH Bonn-Rhein-Sieg, SS 04
139
Peter Becker, Wissensbasierte Systeme I — FH Bonn-Rhein-Sieg, SS 04
141
3. Inferenz in der Logik
Aussagenlogik
3. Inferenz in der Logik
Aussagenlogik
Normalformen
Semantische Äquivalenz
Beispiel 3.8. Syntaktisch unterschiedliche Formel können identische Wahrheitswerte haben. Man betrachte die Formeln ¬(F ∨ G) und ¬F ∧ ¬G:
F
f
f
w
w
G
f
w
f
w
¬(F ∨ G)
w
f
f
f
¬F ∧ ¬G
w
f
f
f
Für die maschinelle Inferenz ist die Darstellung einer Formel in einer standardisierten
und möglichst einfachen Form wichtig.
Definition 3.9.
• Eine Formel F ist ein Literal gdw. F eine atomare Formel oder die Negation einer
atomaren Formel ist.
• Eine Formel F ist in konjunktiver Normalform (KNF) gdw. F eine Konjunktion von
Disjunktionen von Literalen ist, d.h.
Definition 3.8. Zwei aussagenlogische Formeln F, G ∈ Formel(Σ) heißen semantisch äquivalent gdw. I(G) = I(F ) für jede Belegung I ∈ Int(Σ) gilt.
Wenn F und G semantisch äquivalent sind, schreiben wir hierfür F ≡ G.
F = ((L1,1 ∨ . . . ∨ L1,m1 ) ∧ . . . ∧ (Ln,1 ∨ . . . ∨ Ln,mn ))
• Eine Formel F ist in disjunktiver Normalform DNF gdw. F eine Disjunktion von
Konjunktionen von Literalen ist, d.h.
F = ((L1,1 ∧ . . . ∧ L1,m1 ) ∨ . . . ∨ (Ln,1 ∧ . . . ∧ Ln,mn ))
Peter Becker, Wissensbasierte Systeme I — FH Bonn-Rhein-Sieg, SS 04
142
3. Inferenz in der Logik
Aussagenlogik
≡
≡
≡
≡
≡
≡
≡
≡
≡
≡
≡
≡
≡
≡
¬F ∨ G
¬F ∧ ¬G
¬F ∨ ¬G
F
F
F
F
F
G∨F
G∧F
(F ∧ G) ∧ H
(F ∨ G) ∨ H
(F ∧ G) ∨ (F ∧ H)
(F ∨ G) ∧ (F ∨ H)
Peter Becker, Wissensbasierte Systeme I — FH Bonn-Rhein-Sieg, SS 04
3. Inferenz in der Logik
144
Aussagenlogik
Beispiel 3.9. Die Formeln
Lemma 3.2. Wichtige semantische Äquivalenzen sind:
F →G
¬(F ∨ G)
¬(F ∧ G)
¬¬F
F ∨F
F ∧F
F ∧ (F ∨ G)
F ∨ (F ∧ G)
F ∨G
F ∧G
F ∧ (G ∧ H)
F ∨ (G ∨ H)
F ∧ (G ∨ H)
F ∨ (G ∧ H)
Peter Becker, Wissensbasierte Systeme I — FH Bonn-Rhein-Sieg, SS 04
(F ∨ ¬G ∨ H) ∧ J und ¬F ∧ G
Implikation
DeMorgan
sind in KNF.
Dop. Negation
Idempotenz
Die Formeln
Absorption
sind in DNF.
(¬F ∧ G) ∨ (¬H ∧ ¬J) und F ∨ ¬G
Kommutativität
Assoziativität
Distributivität
143
Peter Becker, Wissensbasierte Systeme I — FH Bonn-Rhein-Sieg, SS 04
145
3. Inferenz in der Logik
Aussagenlogik
3. Inferenz in der Logik
Aussagenlogik
ist die Menge
Transformation in Normalform
F = {{L1,1 , . . . , L1,m1 }, . . . , {Ln,1, . . . , Ln,mn }}
Umformungsregeln für KNF/DNF-Transformation:
Schritt 1
Schritt 2
Schritt 3 (KNF)
Schritt 3 (DNF)
F →G
¬¬F
¬(F ∧ G)
¬(F ∨ G)
F ∨ (G ∧ H)
(F ∧ G) ∨ H
F ∧ (G ∨ H)
(F ∨ G) ∧ H
7→
7→
7
→
7→
7
→
7→
7
→
7→
¬F ∨ G
F
¬F ∨ ¬G
¬F ∧ ¬G
(F ∨ G) ∧ (F ∨ H)
(F ∨ H) ∧ (G ∨ H)
(F ∧ G) ∨ (F ∧ H)
(F ∧ H) ∨ (G ∧ H)
Peter Becker, Wissensbasierte Systeme I — FH Bonn-Rhein-Sieg, SS 04
3. Inferenz in der Logik
146
Aussagenlogik
Klauselform
3. Inferenz in der Logik
148
Aussagenlogik
Resolution
Für die maschinelle Inferenz benutzt man eine Mengendarstellung der KNF, die sogenannte Klauselform.
Beispiel 3.10. Resolution basiert auf folgendem Schema:
• Wenn es regnet (R), gehe ich ins Kino (K ), also R → K .
• Wenn es nicht regnet (¬R), gehe ich ins Schwimmbad (S ), also ¬R → S .
• Hieraus folgt, daß ich ins Kino oder ins Schwimmbad gehe, also
Definition 3.10.
• Eine Klausel ist eine Menge von Literalen {L1 , . . . , Ln }, die der Disjunktion L1 ∨
. . . ∨ Ln entspricht.
• Die Klausel {} ist die leere Klausel. Sie wird in der Form 2 geschrieben und entspricht dem Wahrheitswert falsch (f, 0).
• Die Klauselform einer Formel F in KNF mit
F = ((L1,1 ∨ . . . ∨ L1,m1 ) ∧ . . . ∧ (Ln,1 ∨ . . . ∨ Ln,mn ))
Peter Becker, Wissensbasierte Systeme I — FH Bonn-Rhein-Sieg, SS 04
Peter Becker, Wissensbasierte Systeme I — FH Bonn-Rhein-Sieg, SS 04
{R → K, ¬R → S} |= K ∨ S
Als Inferenzregel geschrieben lautet die Resolution wie folgt:
F → G, ¬F → H
G∨H
Für die maschinelle Inferenz benutzt man Resolution in Verbindung mit Klauselform.
147
Peter Becker, Wissensbasierte Systeme I — FH Bonn-Rhein-Sieg, SS 04
149
3. Inferenz in der Logik
Aussagenlogik
3. Inferenz in der Logik
Aussagenlogik
{A}
Definition 3.11. Seien K1, K2 Klauseln und sei A eine atomare Formel mit A ∈ K1
und ¬A ∈ K2. Dann heißt die Klausel R mit
{¬A}
R = (K1 \ {A}) ∪ (K2 \ {¬A})
2
Resolvente von K1 und K2.
Peter Becker, Wissensbasierte Systeme I — FH Bonn-Rhein-Sieg, SS 04
150
3. Inferenz in der Logik
Aussagenlogik
Peter Becker, Wissensbasierte Systeme I — FH Bonn-Rhein-Sieg, SS 04
152
3. Inferenz in der Logik
Aussagenlogik
Beispiel 3.12. Herleitung der Aussage aus Beispiel 3.6 mit der Resolutiosregel:
Ein Resolutionsschritt wird wie folgt dargestellt:
K1
K2
{H, K, M }
{¬H, F }
{F, K, M }
{¬W, ¬K}
R
Beispiel 3.11. Modus Ponens und Modus Tollens können als Spezialfall der Resolution dargestellt werden:
{A}
{¬A, B}
{¬B}
{B}
{¬W, F, M }
{B, ¬A}
{¬A}
Die Resolvente zweier widersprüchlicher Klauseln ist die leere Klausel:
Peter Becker, Wissensbasierte Systeme I — FH Bonn-Rhein-Sieg, SS 04
151
Peter Becker, Wissensbasierte Systeme I — FH Bonn-Rhein-Sieg, SS 04
153
3. Inferenz in der Logik
Aussagenlogik
• Das letzte Beispiel zeigt den direkten Beweis einer Formel mit Hilfe der Resolutionsregeln.
• Beim Resolutionskalkül führt man stattdessen einen Widerspruchsbeweis.
• D.h., man beweist F |= G, in dem man zeigt, daß F ∧ ¬G unerfüllbar ist (vgl.
Satz 3.1).
• Dies bedeutet, man leitet aus den Klauseln von F vereinigt mit den Klauseln, die
sich aus ¬G ergeben, die leere Klausel ab.
3. Inferenz in der Logik
Aussagenlogik
Beispiel 3.13. Herleitung der Aussage aus Beispiel 3.6 mit dem Resolutionskalkül:
Klauselmenge V der Voraussetzungen:
{{H, K, M }, {¬W, ¬K}, {¬H, F }}
Klauselmenge A der negierten zu beweisenden Aussage:
{{W }, {¬F }, {¬M }}
Satz 3.3. Es sei F eine Klauselmenge und es seien K1, K2 ∈ F . Für eine Resolvente R von K1 und K2 gilt F |= R.
Es gilt, aus V ∪ A die leere Klausel abzuleiten.
Insbesondere ist F genau dann erfüllbar, wenn F ∪ {R} erfüllbar ist.
• Satz 3.3 sagt aus, daß durch die Hinzunahme von Resolventen die Erfüllbarkeitseigenschaft einer Klauselmenge nicht beeinträchtigt wird.
• Dies nutzt man im Resolutionskalkül aus. Um zu zeigen, daß eine Klauselmenge
F unerfüllbar ist, bildet man solange Resolventen und fügt sie der Klauselmenge
hinzu, bis irgendwann eine Menge F 0 entsteht, die die leere Klausel enthält.
Peter Becker, Wissensbasierte Systeme I — FH Bonn-Rhein-Sieg, SS 04
3. Inferenz in der Logik
154
Aussagenlogik
• Diese Klauselmenge F 0 ist unerfüllbar, also muß auch die ursprüngliche Klauselmenge F unerfüllbar sein.
Peter Becker, Wissensbasierte Systeme I — FH Bonn-Rhein-Sieg, SS 04
156
3. Inferenz in der Logik
Aussagenlogik
{H, K, M }
{¬M }
{¬H, F }
{H, K}
{¬F }
{¬H}
{K}
{¬W, ¬K}
{¬W }
{W }
2
Peter Becker, Wissensbasierte Systeme I — FH Bonn-Rhein-Sieg, SS 04
155
Peter Becker, Wissensbasierte Systeme I — FH Bonn-Rhein-Sieg, SS 04
157
3. Inferenz in der Logik
Aussagenlogik
3. Inferenz in der Logik
Aussagenlogik
0
Eigenschaften der Resolution
Lemma 3.5. Es sei F eine Klauselmenge. F sei eine Klauselmenge,
Satz 3.4. Eine Klauselmenge F ist unerfüllbar genau dann, wenn die leere Klausel
2 mit einer endlichen Anzahl von Resolutionsschritten aus F abgeleitet werden kann.
Bemerkung 3.3. Aus Satz 3.4 folgt die Korrektheit und (Widerlegungs)-Vollst ändigkeit des Resolutionskalküls:
• die durch sukzessive Resolventenbildung aus F entstanden ist.
• F 0 enthalte nicht die leere Klausel und
• aus F 0 kann keine neue Resolvente erzeugt werden.
Dann ist F 0 und somit auch F erfüllbar.
Beweis. Tafel ✎. 2
• Die leere Klausel kann nur dann abgeleitet werden, wenn die ursprüngliche Klauselmenge unerfüllbar ist =⇒ Korrektheit
• Das Resolutionskalkül findet für jede unerfüllbare Klauselmenge eine Widerlegung,
d.h. die leere Klausel wird abgeleitet =⇒ Vollständigkeit
Peter Becker, Wissensbasierte Systeme I — FH Bonn-Rhein-Sieg, SS 04
3. Inferenz in der Logik
158
Aussagenlogik
• Im Fall der Aussagenlogik ist es entscheidbar, ob die leere Klausel abgeleitet werden kann.
• Für n Aussagenvariablen gibt es höchstens 4n verschiedene Klauseln, die aus
diesen Aussagenvariablen gebildet werden können.
• Der Prozess der Resolventenbildung ist also endlich, d.h. irgendwann k önnen keine neuen Resolventen mehr gebildet werden.
Peter Becker, Wissensbasierte Systeme I — FH Bonn-Rhein-Sieg, SS 04
159
Peter Becker, Wissensbasierte Systeme I — FH Bonn-Rhein-Sieg, SS 04
3. Inferenz in der Logik
160
Aussagenlogik
Fazit zur Aussagenlogik
• Eine Signatur legt die Variablen der Sprache fest.
• Aus den Variablen entsteht durch Festlegung einer Syntax eine Wissensrepr äsentationssprache (Menge der Formeln).
• Eine Interpretation gibt den Variablen eine Bedeutung.
• Die Erfüllungsrelation dehnt diese Bedeutung auf alle Formeln aus
• Über die Erfüllungsrelation wird der Begriff der semantischen Folgerung festgelegt.
• Ein Kalkül stellt die Äquivalenz zwischen semantischer Folgerung und syntaktischen Operationen her.
Peter Becker, Wissensbasierte Systeme I — FH Bonn-Rhein-Sieg, SS 04
161