Teilchenbewegung durch Ueberlagerung von elektrischen und

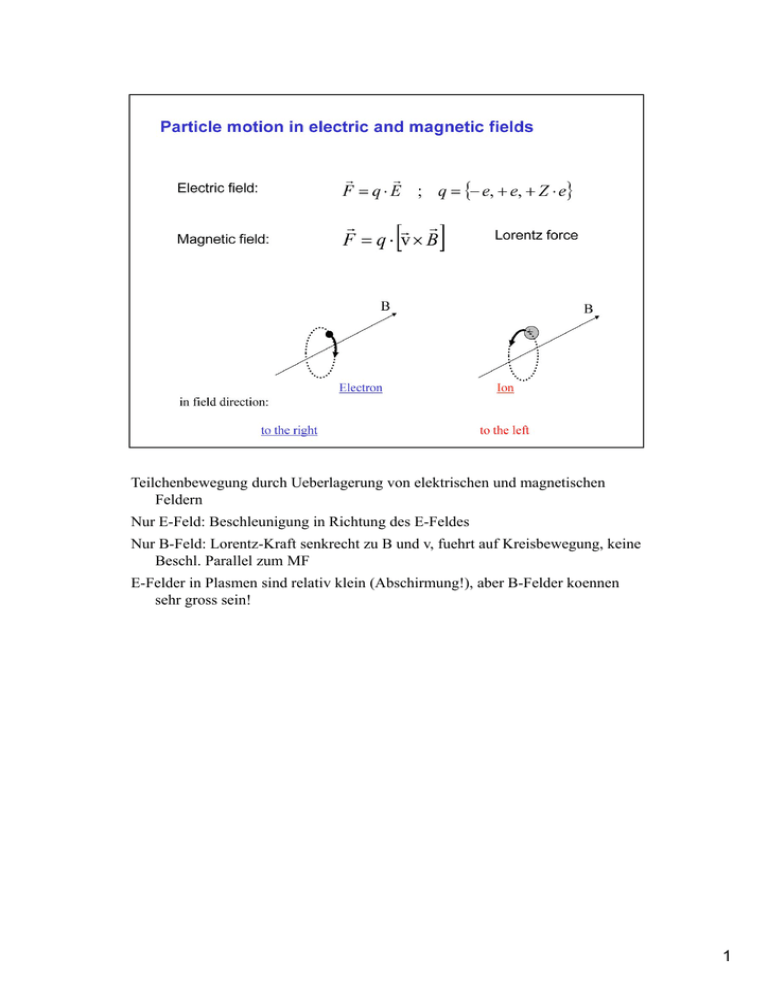
Teilchenbewegung durch Ueberlagerung von elektrischen und magnetischen
Feldern
Nur E-Feld: Beschleunigung in Richtung des E-Feldes
Nur B-Feld: Lorentz-Kraft senkrecht zu B und v, fuehrt auf Kreisbewegung, keine
Beschl. Parallel zum MF
E-Felder in Plasmen sind relativ klein (Abschirmung!), aber B-Felder koennen
sehr gross sein!
1
Gyrationsfrequenz ergibt sich aus Kompensation der Zentrifugalkraft auf einer
Kreisbahn (m omega^2 r) und der Lorentzkraft (q omega r B) -> omega= |q| B/m
Frequenz ist positiv, aber Vorzeichen von q entscheidet ueber Drehsinn
Elektronenfrequenz >> Ionenfrequenz (Massenverhaeltnis), om_ce[Hz]=1.76
10^11 B[T]
In Fusionsplasmen: f_ci~30-60 MHz, f_ce~100-150 GHz
Gyrationsradius: aus gegebenem omega und v_perp=r omega,
ausserdem ½ m v_perp^2=k_B T (2 Freiheitsgrade senkrecht zu B) ->
Gyrationsradien in thermischen Plasmen
Bsp: Fusionsplasma bei 2T, 1 keV: R_Le=53 mu m, r_Li=2.2mm ->
Gyrationsradien viel kleiner als Systemlaenge, d.h magnetisiertes Plasma
(Teilchen folgen Feldlinien, wegen endlicher Parallelgeschwindigkeit ist
Bewegung auf Schraubenlinie laengs des Magnetfeldes)
Teilchenbewegung erzeugt Kreisstrom, der MF erzeugt, das urspruenglichem MF
entgegengerichtet ist, d.h. ein Einzelteilchen verhaelt sich
Diagmagnetisch (wegen Stromdefinition an Ionenbewegung)
.
2
3
Gyrationsfrequenz ergibt sich aus Kompensation der Zentrifugalkraft auf einer
Kreisbahn (m omega^2 r) und der Lorentzkraft (q omega r B) -> omega= |q| B/m
Frequenz ist positiv, aber Vorzeichen von q entscheidet ueber Drehsinn
Elektronenfrequenz >> Ionenfrequenz (Massenverhaeltnis), om_ce[Hz]=1.76
10^11 B[T]
In Fusionsplasmen: f_ci~30-60 MHz, f_ce~100-150 GHz
Gyrationsradius: aus gegebenem omega und v_perp=r omega,
ausserdem ½ m v_perp^2=k_B T (2 Freiheitsgrade senkrecht zu B) ->
Gyrationsradien in thermischen Plasmen
Bsp: Fusionsplasma bei 2T, 1 keV: R_Le=53 mu m, r_Li=2.2mm ->
Gyrationsradien viel kleiner als Systemlaenge, d.h magnetisiertes Plasma
(Teilchen folgen Feldlinien, wegen endlicher Parallelgeschwindigkeit ist
Bewegung auf Schraubenlinie laengs des Magnetfeldes)
Teilchenbewegung erzeugt Kreisstrom, der MF erzeugt, das urspruenglichem MF
entgegengerichtet ist, d.h. ein Einzelteilchen verhaelt sich
Diagmagnetisch (wegen Stromdefinition an Ionenbewegung)
.
4
5
Gyrationsfrequenz ergibt sich aus Kompensation der Zentrifugalkraft auf einer
Kreisbahn (m omega^2 r) und der Lorentzkraft (q omega r B) -> omega= |q| B/m
Frequenz ist positiv, aber Vorzeichen von q entscheidet ueber Drehsinn
Elektronenfrequenz >> Ionenfrequenz (Massenverhaeltnis), om_ce[Hz]=1.76
10^11 B[T]
In Fusionsplasmen: f_ci~30-60 MHz, f_ce~100-150 GHz
Gyrationsradius: aus gegebenem omega und v_perp=r omega,
ausserdem ½ m v_perp^2=k_B T (2 Freiheitsgrade senkrecht zu B) ->
Gyrationsradien in thermischen Plasmen
Bsp: Fusionsplasma bei 2T, 1 keV: R_Le=53 mu m, r_Li=2.2mm ->
Gyrationsradien viel kleiner als Systemlaenge, d.h magnetisiertes Plasma
(Teilchen folgen Feldlinien, wegen endlicher Parallelgeschwindigkeit ist
Bewegung auf Schraubenlinie laengs des Magnetfeldes)
Teilchenbewegung erzeugt Kreisstrom, der MF erzeugt, das urspruenglichem MF
entgegengerichtet ist, d.h. ein Einzelteilchen verhaelt sich
Diagmagnetisch (wegen Stromdefinition an Ionenbewegung)
.
6
Gyration entspricht Beschleunigung der Ladung, daher strahlt Elektron mit
Gyrationsfrequenz (und wegen relativistischer Effekte auch bei den
Harmonischen) ab
Emissivitaet vor allem bei Grundfrequenz und niedrigen Oberwellen sehr hoch,
so dass Strahlung oft optisch dick ist, dann kann man aus Absolutintensitaet
Wegen B_nu(T) eine Elektronen-Temperatur zuordnen
Gyrationsfreqeunz ist bei viel kleineren Werten als Maximum der Planck-Kurve,
man kann fuer kleine Frequenzen entwickeln ->Strahlung proportional zu T
(entspricht Rayleigh-Jeans-Gesetz)
Ort der Temperaturmessung laesst sich im inhomogenen Magnetfeld direkt aus
Gyrationsfrequenz (~B) bestimmen
Fuer Ionen geht das nicht, da Strahlung wegen geringerer Kreisbeschleunigung
viel geringer und daher nicht optisch dick ist
Heizung durch Einstrahlung von Wellen an Elektronen- oder IonenZyklotronfrequenz (siehe Plasmawellen)
7
Gyration entspricht Beschleunigung der Ladung, daher strahlt Elektron mit
Gyrationsfrequenz (und wegen relativistischer Effekte auch bei den
Harmonischen) ab
Emissivitaet vor allem bei Grundfrequenz und niedrigen Oberwellen sehr hoch,
so dass Strahlung oft optisch dick ist, dann kann man aus Absolutintensitaet
Wegen B_nu(T) eine Elektronen-Temperatur zuordnen
Gyrationsfreqeunz ist bei viel kleineren Werten als Maximum der Planck-Kurve,
man kann fuer kleine Frequenzen entwickeln ->Strahlung proportional zu T
(entspricht Rayleigh-Jeans-Gesetz)
Ort der Temperaturmessung laesst sich im inhomogenen Magnetfeld direkt aus
Gyrationsfrequenz (~B) bestimmen
Fuer Ionen geht das nicht, da Strahlung wegen geringerer Kreisbeschleunigung
viel geringer und daher nicht optisch dick ist
Heizung durch Einstrahlung von Wellen an Elektronen- oder IonenZyklotronfrequenz (siehe Plasmawellen)
8
Zusaetzlich zur Lorentz-Kraft kann weiter Kraft auftreten (z.B. elektrisches Feld).
MF beeinflusst nur Dynamik senkrecht zu B
Fuer raeumlich und zeitlich konstantes MF und F: guiding centre Ansatz: die
durch F verursachte Bewegung wird Gyration ueberlagert
-> Bewegung des “Fuehrungszentrums” (r_c) (Kreismittelpunkt) ueberlagert
durch Gyration (r_g) um Fuehrungszentrum herum
r_g wird genommen mit Betrag des Lamor-Radius, Richtung gewaehlt, so dass
Vektor zum Zentrum zeigt
9
Bewegungsgleichung mit v=dr/dt und Bewegungsgleicgung fuer v
(vxB)xB=(v B)B-B^2v= B^2 v_|| -B^2 v = -B^2 v_perp
Parallele Bewegung gegeben durch m d^2v_||dt^2=F_||
Senkrechte Bewegung ist Drift, denn trotz konstanter Kraft keine
Beschleunigung,
Nur der Teil der Kraft senkrecht zum MF fuehrt auf Drift
10
Bewegungsgleichung mit v=dr/dt und Bewegungsgleicgung fuer v
(vxB)xB=(v B)B-B^2v= B^2 v_|| -B^2 v = -B^2 v_perp
Parallele Bewegung gegeben durch m d^2v_||dt^2=F_||
Senkrechte Bewegung ist Drift, denn trotz konstanter Kraft keine
Beschleunigung,
Nur der Teil der Kraft senkrecht zum MF fuehrt auf Drift
11
Bild: Hier angenommmen, dass beide Teilchen: e und I sich parallel zum MF in
gleiche Richtung bewegen (das ist bei Bewegung wegen angelegtem E-Feld
natuerlich nciht der Fall), Beschl. wegen Def. des E-Feldes (+-> -), graue Pfeile
zeigen Driftrichtung (rote und blaube Bewegubgsrichtung)
Aenderung des Gyrationsradius wegen Aenderung der Senkrechtgeschw. (E-Feld
beschl. in Richtung des Feldes, die ist senkrecht zu B)
- Drift ist ladungsunabhaengig und produziert daher keinen Strom
Drift verschwindet im mitbewegten System: Lorentz-Transformation: man kann
ein neues E-Feld einfuehren: E’= E + v_D x B,
das ist das E-Feld fuer mitbewegtes System, E-Feld durch v_DxB zeigt in
entgegengesetzte Richtung von E,
V_D x B= (ExB) x B/B^2=-B x (ExB)/B^2= - vec(E)
12
Bild: Hier angenommmen, dass beide Teilchen: e und I sich parallel zum MF in
gleiche Richtung bewegen (das ist bei Bewegung wegen angelegtem E-Feld
natuerlich nciht der Fall), Beschl. wegen Def. des E-Feldes (+-> -), graue Pfeile
zeigen Driftrichtung (rote und blaube Bewegubgsrichtung)
Aenderung des Gyrationsradius wegen Aenderung der Senkrechtgeschw. (E-Feld
beschl. in Richtung des Feldes, die ist senkrecht zu B)
- Drift ist ladungsunabhaengig und produziert daher keinen Strom
Drift verschwindet im mitbewegten System: Lorentz-Transformation: man kann
ein neues E-Feld einfuehren: E’= E + v_D x B,
das ist das E-Feld fuer mitbewegtes System, E-Feld durch v_DxB zeigt in
entgegengesetzte Richtung von E,
V_D x B= (ExB) x B/B^2=-B x (ExB)/B^2= - vec(E)
13
14
15
16
- Bisher war vorausgesetzt, dass MF homogen war, guiding centre bleibt guter
Ansatz, so lange grad B << B/r_L
-Eigentlich ist F=grad(mu B), aber Ringstrom durch Gyration erzeugt (wie auf
S.1 dieser Vorlesung) magnetisches
Moment, das B entgegengerichtet ist, daher F=-mu B
Magnetisches Moment: mit Gyro-Bewegung verbundener Kreisstrom mal von
Strom umrandeter Flaeche
In einem geraden Leiter der Laenge L : I = q v/ L
bei Kreisstrom: L = 2 pi r, I = q v /(2 pi r), v=omega/r -> I = q omega/(2 pi)
Flaeche des Kreises: pi r_L^2
Setze Gyrationsfrequenz: omega=q B/m ein und r_L = m v_perp/(qB)
17
- Bisher war vorausgesetzt, dass MF homogen war, guiding centre bleibt guter
Ansatz, so lange grad B << B/r_L
-Eigentlich ist F=grad(mu B), aber Ringstrom durch Gyration erzeugt (wie auf
S.1 dieser Vorlesung) magnetisches
Moment, das B entgegengerichtet ist, daher F=-mu B
Magnetisches Moment: mit Gyro-Bewegung verbundener Kreisstrom mal von
Strom umrandeter Flaeche
In einem geraden Leiter der Laenge L : I = q v/ L
bei Kreisstrom: L = 2 pi r, I = q v /(2 pi r), v=omega/r -> I = q omega/(2 pi)
Flaeche des Kreises: pi r_L^2
Setze Gyrationsfrequenz: omega=q B/m ein und r_L = m v_perp/(qB)
18
- Bisher war vorausgesetzt, dass MF homogen war, guiding centre bleibt guter
Ansatz, so lange grad B << B/r_L
-Eigentlich ist F=grad(mu B), aber Ringstrom durch Gyration erzeugt (wie auf
S.1 dieser Vorlesung) magnetisches
Moment, das B entgegengerichtet ist, daher F=-mu B
Magnetisches Moment: mit Gyro-Bewegung verbundener Kreisstrom mal von
Strom umrandeter Flaeche
In einem geraden Leiter der Laenge L : I = q v/ L
bei Kreisstrom: L = 2 pi r, I = q v /(2 pi r), v=omega/r -> I = q omega/(2 pi)
Flaeche des Kreises: pi r_L^2
Setze Gyrationsfrequenz: omega=q B/m ein und r_L = m v_perp/(qB)
19
Anschaulich: eine Verstaerkung des MF bedeutet engere MF-Linien, die dabei
natuerlich gekruemmt sind
- Relevante Kraft: Zentrifugalkraft : - m om (om x r)= m omega^2 vec( r) (wenn
omega perp to r) = m v_||^2/r vec( r)
- relevanter Radiusvektor ist lokaler Kruemmungsradius
20
Anschaulich: eine Verstaerkung des MF bedeutet engere MF-Linien, die dabei
natuerlich gekruemmt sind
- Relevante Kraft: Zentrifugalkraft : - m om (om x r)= m omega^2 vec( r) (wenn
omega perp to r) = m v_||^2/r vec( r)
- relevanter Radiusvektor ist lokaler Kruemmungsradius
21
Anschaulich: eine Verstaerkung des MF bedeutet engere MF-Linien, die dabei
natuerlich gekruemmt sind
- Relevante Kraft: Zentrifugalkraft : - m om (om x r)= m omega^2 vec( r) (wenn
omega perp to r) = m v_||^2/r vec( r)
- relevanter Radiusvektor ist lokaler Kruemmungsradius
22
Gyrationsfrequenz ergibt sich aus Kompensation der Zentrifugalkraft auf einer
Kreisbahn (m omega^2 r) und der Lorentzkraft (q omega r B) -> omega= |q| B/m
Frequenz ist positiv, aber Vorzeichen von q entscheidet ueber Drehsinn
Elektronenfrequenz >> Ionenfrequenz (Massenverhaeltnis), om_ce[Hz]=1.76
10^11 B[T]
In Fusionsplasmen: f_ci~30-60 MHz, f_ce~100-150 GHz
Gyrationsradius: aus gegebenem omega und v_perp=r omega,
ausserdem ½ m v_perp^2=k_B T (2 Freiheitsgrade senkrecht zu B) ->
Gyrationsradien in thermischen Plasmen
Bsp: Fusionsplasma bei 2T, 1 keV: R_Le=53 mu m, r_Li=2.2mm ->
Gyrationsradien viel kleiner als Systemlaenge, d.h magnetisiertes Plasma
(Teilchen folgen Feldlinien, wegen endlicher Parallelgeschwindigkeit ist
Bewegung auf Schraubenlinie laengs des Magnetfeldes)
Teilchenbewegung erzeugt Kreisstrom, der MF erzeugt, das urspruenglichem MF
entgegengerichtet ist, d.h. ein Einzelteilchen verhaelt sich
Diagmagnetisch (wegen Stromdefinition an Ionenbewegung)
.
23
Zusaetzlich zur Lorentz-Kraft kann weiter Kraft auftreten (z.B. elektrisches Feld).
MF beeinflusst nur Dynamik senkrecht zu B
Fuer raeumlich und zeitlich konstantes MF und F: guiding centre Ansatz: die
durch F verursachte Bewegung wird Gyration ueberlagert
-> Bewegung des “Fuehrungszentrums” (r_c) (Kreismittelpunkt) ueberlagert
durch Gyration (r_g) um Fuehrungszentrum herum
r_g wird genommen mit Betrag des Lamor-Radius, Richtung gewaehlt, so dass
Vektor zum Zentrum zeigt
24
25
Man muss die entstehenden E-Felder kurzschliessen, d.h. MF-Linein muessen
Komponente von unten nach oben haben, d.h. endliche Steigung
Der MF-Linien noetig (im Tokamak fliesst daher Plasmastrom)
26
Fuer periodische Bewegungen neben Energie, Impuls- Drehimpulserhaltung
weitere Invarianten der Bewegung,dabei
Sind p und q kanonisch konjugierter Ort und Impuls.
Hier haben wir es bei der Gyration mit einer fast perioischen Bewegung zu tun,
wenn sich MF raeumlich und zeitlich nur langsam aendert
Fuer kanonisch konjugierte Koordinaten gilt: H=sum_i (q_i p_i )-L, q_i, p_I:
kanonisch konjugierter ort und Impuls
H=E_kin+E_pot, L=E_kin-E_pot
Fuer periodische Bewegung gilt int(delta H)=int(delta L)= int (p del q) =0 (nach
einer periodischen Bewegung ist Energieaenderung verschwunden
Kanonisch konjugierter Impuyls und ort fuer Elektron im elektromagnetischen
Feld aus theoretischer Mechanik
In Zylinderkoord. Mit homogenem MF in z-Richtung -> Rotation mit endlichem
Radius r in phi-Richtung -> dq_phi=v_phi dt
Homogenes B_z-Feld findet man aus z-Komponente von rot A_phi=1/r(d/dr(r
A_phi))=const (alle anderen Komponenten von rot A_phi=0),
Man kann zeigen dass rot A_phi =B ist
r_g=m v_phi/(e B) -> e A_phi=m/2 v_phi
v_phi dt = r_g d phi
27
Mit r_g = m v_phi/(q B) folgt: (3/2) 2 pi m^2 v_phi^2/(q B)
Mit mu= m/2 v_phi^2 /B _> 6 pi m/q
27
Fuer periodische Bewegungen neben Energie, Impuls- Drehimpulserhaltung
weitere Invarianten der Bewegung,dabei
Sind p und q kanonisch konjugierter Ort und Impuls.
Hier haben wir es bei der Gyration mit einer fast perioischen Bewegung zu tun,
wenn sich MF raeumlich und zeitlich nur langsam aendert
Fuer kanonisch konjugierte Koordinaten gilt: H=sum_i (q_i p_i )-L, q_i, p_I:
kanonisch konjugierter ort und Impuls
H=E_kin+E_pot, L=E_kin-E_pot
Fuer periodische Bewegung gilt int(delta H)=int(delta L)= int (p del q) =0 (nach
einer periodischen Bewegung ist Energieaenderung verschwunden
Kanonisch konjugierter Impuyls und ort fuer Elektron im elektromagnetischen
Feld aus theoretischer Mechanik
In Zylinderkoord. Mit homogenem MF in z-Richtung -> Rotation mit endlichem
Radius r in phi-Richtung -> dq_phi=v_phi dt
Homogenes B_z-Feld findet man aus z-Komponente von rot A_phi=1/r(d/dr(r
A_phi))=const (alle anderen Komponenten von rot A_phi=0),
Man kann zeigen dass rot A_phi =B ist
r_g=m v_phi/(e B) -> e A_phi=m/2 v_phi
v_phi dt = r_g d phi
28
Mit r_g = m v_phi/(q B) folgt: (3/2) 2 pi m^2 v_phi^2/(q B)
Mit mu= m/2 v_phi^2 /B _> 6 pi m/q
28
Fuer periodische Bewegungen neben Energie, Impuls- Drehimpulserhaltung
weitere Invarianten der Bewegung,dabei
Sind p und q kanonisch konjugierter Ort und Impuls.
Hier haben wir es bei der Gyration mit einer fast perioischen Bewegung zu tun,
wenn sich MF raeumlich und zeitlich nur langsam aendert
Fuer kanonisch konjugierte Koordinaten gilt: H=sum_i (q_i p_i )-L, q_i, p_I:
kanonisch konjugierter ort und Impuls
H=E_kin+E_pot, L=E_kin-E_pot
Fuer periodische Bewegung gilt int(delta H)=int(delta L)= int (p del q) =0 (nach
einer periodischen Bewegung ist Energieaenderung verschwunden
Kanonisch konjugierter Impuyls und ort fuer Elektron im elektromagnetischen
Feld aus theoretischer Mechanik
In Zylinderkoord. Mit homogenem MF in z-Richtung -> Rotation mit endlichem
Radius r in phi-Richtung -> dq_phi=v_phi dt
Homogenes B_z-Feld findet man aus z-Komponente von rot A_phi=1/r(d/dr(r
A_phi))=const (alle anderen Komponenten von rot A_phi=0),
Man kann zeigen dass rot A_phi =B ist
r_g=m v_phi/(e B) -> e A_phi=m/2 v_phi
v_phi dt = r_g d phi
29
Mit r_g = m v_phi/(q B) folgt: (3/2) 2 pi m^2 v_phi^2/(q B)
Mit mu= m/2 v_phi^2 /B _> 6 pi m/q
29
Fuer periodische Bewegungen neben Energie, Impuls- Drehimpulserhaltung
weitere Invarianten der Bewegung,dabei
Sind p und q kanonisch konjugierter Ort und Impuls.
Hier haben wir es bei der Gyration mit einer fast perioischen Bewegung zu tun,
wenn sich MF raeumlich und zeitlich nur langsam aendert
Fuer kanonisch konjugierte Koordinaten gilt: H=sum_i (q_i p_i )-L, q_i, p_I:
kanonisch konjugierter ort und Impuls
H=E_kin+E_pot, L=E_kin-E_pot
Fuer periodische Bewegung gilt int(delta H)=int(delta L)= int (p del q) =0 (nach
einer periodischen Bewegung ist Energieaenderung verschwunden
Kanonisch konjugierter Impuyls und ort fuer Elektron im elektromagnetischen
Feld aus theoretischer Mechanik
In Zylinderkoord. Mit homogenem MF in z-Richtung -> Rotation mit endlichem
Radius r in phi-Richtung -> dq_phi=v_phi dt
Homogenes B_z-Feld findet man aus z-Komponente von rot A_phi=1/r(d/dr(r
A_phi))=const (alle anderen Komponenten von rot A_phi=0),
Man kann zeigen dass rot A_phi =B ist
r_g=m v_phi/(e B) -> e A_phi=m/2 v_phi
v_phi dt = r_g d phi
30
Mit r_g = m v_phi/(q B) folgt: (3/2) 2 pi m^2 v_phi^2/(q B)
Mit mu= m/2 v_phi^2 /B _> 6 pi m/q
30
Laeuft Teilchen in Gebiet mit hoeherem MF, nimmt seine Senkrechtenergie zu
(prop to B), weil aber gleichzeitig Energieerhaltung gilt,
Muss Parallelenergie abnehmen -> Teilchen wandelt Parallel- in Senkrechtenergie
um
Ds kann gehen bis v_|| = 0, dann wird Teilchen reflektiert
31
Aus Erhaltung des magnetischen Moments folgt:
Spiegelbedingung: Energie bei Durchlauf durch B-Minimum: m/2 (v_perp(0)^2 +
v_||^2) muss kleiner sein als m/2 v_perp(max)^2
v_perp(max)^2/v_perp(0)^2 = B_max/B_min -> m/2 (v_perp(0)^2 + v_||^2) <
m/2 B_max/B_min v_perp(0)^2
32
Aus Erhaltung des magnetischen Moments folgt:
Spiegelbedingung: Energie bei Durchlauf durch B-Minimum: m/2 (v_perp(0)^2 +
v_||^2) muss kleiner sein als m/2 v_perp(max)^2
v_perp(max)^2/v_perp(0)^2 = B_max/B_min -> m/2 (v_perp(0)^2 + v_||^2) <
m/2 B_max/B_min v_perp(0)^2
33
34
Teilchenbeschuss von Oberflaechen:
(primär geht die Parallelbewegung in die Elektronen,
diese ziehen dann aber die Ionen wegen der
Quasineutralitätsbedingung mit!)
35
Eine zur Spiegelmaschine analoge Konfiguration produziert das MF der Erde
Feldstaerke nimmt zu den Polen hin zu
Energiereiche Teilchen aus dem Sonnenwind koennen in diesem Feld durch
Stoesse eingefangen werden
Diese pendeln (wenn v_perp/v_|| ausreichend gross ist) zwischen Polen hin und
her
36
Die in dem van-Allen-Guertel gespeicherten Teilchen koennen durch Stoesse in
den Verlustkegel geraten und auf die Erde stroemen,
dort verursachen sie Polarlichter
37
38
Eine zur Spiegelmaschine analoge Konfiguration produziert das MF der Erde
Feldstaerke nimmt zu den Polen hin zu
Energiereiche Teilchen aus dem Sonnenwind koennen in diesem Feld durch
Stoesse eingefangen werden
Diese pendeln (wenn v_perp/v_|| ausreichend gross ist) zwischen Polen hin und
her
39
Eine zur Spiegelmaschine analoge Konfiguration produziert das MF der Erde
Feldstaerke nimmt zu den Polen hin zu
Energiereiche Teilchen aus dem Sonnenwind koennen in diesem Feld durch
Stoesse eingefangen werden
Diese pendeln (wenn v_perp/v_|| ausreichend gross ist) zwischen Polen hin und
her
1T=1Vs/m^2
40
41
3. Adiabatische Invariante ist wichtig, weil sie beweist, dass im
axialsymmetrischen Tokamak die Teilchen eingeschlossen bleiben
42
Bei hohen Teilchenenergien wird Gyro-Radius vergleichbar mit
Kruemmungsradius der Feldliniien, dann geht “guiding”-centre-Ansatz nicht
mehr
-> Teilchenbahnen muessen berechnet werden aus Integration der
Bewegungsgleichungen
43
E-Feld darf sich nur langsam gegen Gyro-Frequenz aendern, sonst gilt GyroZentrumsnaeherung nicht
Wegen m dv_D/dt erfaaehrt Teilchen eine Beschleunigungskraft, die senkrecht zu
B ist (wenn E senkrecht zu B),
das bewirkt wieder eine Drift
Anschaulich: eigentlich Drift nach oben, aber waehrend jeder Gyration wird EFeld in x-Richtung groesser ->
Teilchen werden mehr als bei zeitlich konstantem E-feld beschleunigt auf dem
Weg in x-Richtung udn abgebremst auf
Dem Weg in negative x-Richtung -> Gryrationsradien wandern langsma in xRichtung
44
E-Feld darf sich nur langsam gegen Gyro-Frequenz aendern, sonst gilt GyroZentrumsnaeherung nicht
Wegen m dv_D/dt erfaaehrt Teilchen eine Beschleunigungskraft, die senkrecht zu
B ist (wenn E senkrecht zu B),
das bewirkt wieder eine Drift
Anschaulich: eigentlich Drift nach oben, aber waehrend jeder Gyration wird EFeld in x-Richtung groesser ->
Teilchen werden mehr als bei zeitlich konstantem E-feld beschleunigt auf dem
Weg in x-Richtung udn abgebremst auf
Dem Weg in negative x-Richtung -> Gryrationsradien wandern langsma in xRichtung
45
E-Feld darf sich nur langsam gegen Gyro-Frequenz aendern, sonst gilt GyroZentrumsnaeherung nicht
Wegen m dv_D/dt erfaaehrt Teilchen eine Beschleunigungskraft, die senkrecht zu
B ist (wenn E senkrecht zu B),
das bewirkt wieder eine Drift
Anschaulich: eigentlich Drift nach oben, aber waehrend jeder Gyration wird EFeld in x-Richtung groesser ->
Teilchen werden mehr als bei zeitlich konstantem E-feld beschleunigt auf dem
Weg in x-Richtung udn abgebremst auf
Dem Weg in negative x-Richtung -> Gryrationsradien wandern langsma in xRichtung
46
E-Feld darf sich nur langsam gegen Gyro-Frequenz aendern, sonst gilt GyroZentrumsnaeherung nicht
Wegen m dv_D/dt erfaaehrt Teilchen eine Beschleunigungskraft, die senkrecht zu
B ist (wenn E senkrecht zu B),
das bewirkt wieder eine Drift
Anschaulich: eigentlich Drift nach oben, aber waehrend jeder Gyration wird EFeld in x-Richtung groesser ->
Teilchen werden mehr als bei zeitlich konstantem E-feld beschleunigt auf dem
Weg in x-Richtung udn abgebremst auf
Dem Weg in negative x-Richtung -> Gryrationsradien wandern langsma in xRichtung
47
48
D: dielectric displacement
49
50
- Anschaulich: mehr Teilchen rechts als links -> dort wo Gyrationsbahnen sicht
treffen, bewegen sich mehr Teilchen nach oben als
Nach unten -> keine Massenbewegung! Trotzdem gibt es einen Strom, weil Ionen
in entgegengesetzte Richtung gyrieren
- Aehnlicher Effekt ergibt sich wenn T von links nach rechts zunimmt: dann ist
rechts die Geschwindigkeit der Einzelteilchen nach oben
Groesser (fuer Ionen nach unten) -> es folgt wieder ein Strom
- Im Bild einer Kraft: auf Volumenelement wirkt eine Kraft, wenn es einen
Druckgradienten gibt:
- Betrachte Kraft auf Fluessigkeitselement mit Volumen delta V: F/delta V = grad p
-im Volumen gibt es delta N = n delta V Teilchen -> Kraft pro Teilchen: F/delta N
= F/(n delta V) =-grad p/n
-Drift ist zwar keine Massenebwegung, aber sie ist von Ladung abhaengig und
erzeugt daher einen Strom
51
52
53
54
55
3. Adiabatische Invariante ist wichtig, weil sie beweist, dass im
axialsymmetrischen Tokamak die Teilchen eingeschlossen bleiben
56