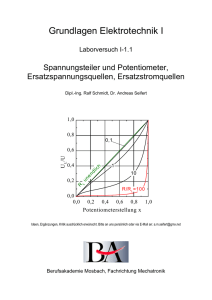
Grundlagen Elektrotechnik I
Werbung

Grundlagen Elektrotechnik I Laborversuch I-2.0 (vorläufige „Nullversion“) Die Wheatstone-Brücke als Abgleich- und Ausschlagbrücke Dipl.-Ing. Ralf Schmidt, Dr. Andreas Seifert Ideen, Ergänzungen, Kritik ausdrücklich erwünscht. Bitte an uns persönlich oder via E-Mail an: [email protected] Berufsakademie Mosbach, Fachrichtung Mechatronik Grundlagen Elektrotechnik I Laborversuch I-2.0 Inhalt 1 1.1 1.2 1.2.1 1.2.2 1.2.3 1.3 1.3.1 1.3.2 Motivation, Vorüberlegungen Die Wheatstone-Brücke Wheatstone-Brücke als Abgleichbrücke Abgleichbedingung Messung eines unbekannten Widerstands Genauigkeit Wheatstone-Brücke als Ausschlagbrücke Ausschlagbrücke im unbelasteten Zustand Ausschlagbrücke im belasteten Zustand 2 2.1 2.2 2.3 2.4 Laborversuche Allgemeines Experiment: Abgleichbrücke Experiment: Ausschlagbrücke ohne Belastung Experiment: Ausschlagbrücke mit Belastung A A1 A2 A3 A4 Anhang Fehlerbetrachtung Potenzreihenentwicklung von Funktionen: Linearisierung Linearisierung der Brückenspannung im belasteten Fall Ausgleichsrechnung, Regressionsanalyse Ausstattung Folgende Geräte mit Zubehör stehen Ihnen zur Verfügung: · Labornetzgerät mit einstellbarer Spannung und Strombegrenzung · Digitalmultimeter · Experimentierbrett und Widerstände · 10-Gang-Wendelpotentiometer · Widerstandsdekade (1 W -11 MW, 1 Watt) · Messleitungen 2 Grundlagen Elektrotechnik I Laborversuch I-2.0 1. Motivation, Vorüberlegungen 1.1 Die Wheatstone-Brücke Die erstmals von Wheatstone verwendete und nach ihm benannte Brückenschaltung ermöglicht die Widerstandsmessung durch einen Vergleich mit bekannten Widerständen. Sie eignet sich zur Messung von Festwiderständen in der Form der Abgleichbrücke und zur Messung von Widerstandsänderungen als Ausschlagbrücke. R1 U1 U3 R3 U4 R4 R5 U DU=U5 R2 U2 1.2 Wheatstone-Brücke als Abgleichbrücke 1.2.1 Abgleichbedingung Die Wheatstone-Brücke kann als „Doppel-Spannungsteiler“ aufgefasst werden, der aus einem Spannungsteiler mit den Widerständen R 1 und R 2 und aus einem Spannungsteiler mit den Widerständen R 3 und R 4 besteht. Die „Brückenspannung“ DU º U 5 ist im Leerlauf ( R 5 = ¥ ) die Differenz der Spannungen R2 R4 U und U , es ist also R1 + R 2 R3 + R4 uuu é R2 R4 ù DU = ê ú U. R R R R + + 1 2 3 4 ë û Für beliebige Versorgungsspannungen U wird DU = 0 , wenn die Abgleichbedingung uuu R1 R 3 = R2 R4 erfüllt ist. Der Wert des Widerstands R 5 hat in diesem Fall keinen Einfluss. 3 Grundlagen Elektrotechnik I Laborversuch I-2.0 1.2.2 Messung eines unbekannten Widerstands Ist ein unbekannter Widerstandswert R 1 zu bestimmen, so kann dieser im Fall der abgegliR chenen Brücke gemäß R 1 = R 2 3 ermittelt werden, wenn die Widerstandswerte R 2 , R 3 R4 und R 4 bekannt sind. Verwendet man als „rechten Spannungsteiler“ ein Potentiometer mit präzise ablesbarer Skala (zum Beispiel 0 £ x £ 1 ), so folgt mit R 3 = (1 - x ) R und R 4 = x R und dem Gesamtwiderstand R des Potentiometers: uuu R1 = R 2 R3 (1 - x ) R 1- x = R2 = R2 R4 xR x R1 U1 R5 R U DU=U5 R2 U2 Nullindikator: In jeder Abgleichbrücke wird ein Nullindikator benötigt. Häufig hat man Drehspulinstrumente mit dem Nullpunkt in der Skalenmitte verwendet. Dabei ist es sinnvoll, eine Umschaltung der Empfindlichkeit vorzusehen, um zunächst einen Grobabgleich mit nachfolgendem Feinabgleich in der Nähe des Abgleichpunkts durchführen zu können. Schließlich bietet die Elektronik mit dem Operationsverstärker sogar die Möglichkeit eines automatischen Brückenabgleichs. Ein Servomotor verstellt den Potentiometerschleifer so lange, bis die Ausgangsspannung des Differenzverstärkers Null wird und damit die Abgleichbedingung erfüllt ist. Wir verwenden bei unseren Experimenten ein Digitalvoltmeter als Nullindikator. 1.2.3 Genauigkeit Bei der Brückenschaltung gehen weder die Versorgungsspannung der Brücke, noch der Innenwiderstand R 5 des Nullindikators in die Bestimmungsgleichung für den unbekannten Widerstand ein. Allerdings besteht ein indirekter Einfluss: Je größer die Versorgungsspannung gewählt wird, desto größer ist natürlich auch die Brückenspannung in der Nähe des Abgleichpunkts. Diese reagiert somit empfindlicher auf Veränderungen der Abgleichwiderstände, und der Abgleich kann mit größerer Genauigkeit durchgeführt werden. Das Nullinstrument muss den Nulldurchgang der Brückenspannung mit großer Präzision anzeigen. Diese Forderung ist grundsätzlich leicht zu erfüllen, da der Nullpunkt durch Kurz4 Grundlagen Elektrotechnik I Laborversuch I-2.0 schließen des Instruments schnell und einfach kontrolliert werden kann. Bei Zeigerinstrumenten kann der Reibungsfehler zu Problemen führen. Je nach dem, von welcher Seite man sich dem Abgleichpunkt nähert (Brückenspannung positiv oder negativ), können sich auf Grund der Reibung Unterschiede im Ergebnis zeigen. Widerstandstoleranzen des Potentiometers wirken sich nicht auf die Genauigkeit des Messergebnisses aus. Unmittelbaren Einfluss auf die Genauigkeit haben allerdings der Fehler DR 2 des Referenzwiderstands und der Fehler Dx des abgelesenen Skalenwerts. Sind diese Fehler zufällig, so findet man für den relativen Fehler des Messergebnisses uuu (DR 2 ) 2 DR 1 ( Dx ) 2 = + . R1 R 22 x 2 (1 - x ) 2 Die Herleitung dieser Gleichung ist in Anhang A1 ausführlich dargestellt. Der relative Fehler DR 1 DR 2 ist immer größer als der relative Fehler des Referenzwiderstands. Bei ungünstiger R1 R2 Wahl des Referenzwiderstands ( R 2 >> R 1 oder R 2 << R 1 ) liegt der Ablesewert von x nahe bei x = 0 oder x = 1 . Hier liefert dann der zweite Term unter der Wurzel einen sehr großen Beitrag. (Aufgabe dazu im Anhang A1) 1.3 Wheatstone-Brücke als Ausschlagbrücke Die abgeglichene Messbrücke ermöglicht eine sehr genaue Messung des Absolutbetrags von Widerstandswerten. Will man jedoch Änderungen des Werts erfassen, dann ist es wesentlich einfacher, diese Widerstandsänderungen aus den Änderungen der Brückenspannung zu ermitteln als durch ständig neues Abgleichen mit nachfolgender Berechnung aus den Abgleichwerten. Damit kommt man zur Ausschlagbrücke, die häufig zur Temperaturmessung mit Widerstandsthermometern oder zur Auswertung von Dehnungsmessungen (Dehnungsmessstreifen) verwendet wird. 1.3.1 Ausschlagbrücke im unbelasteten Zustand Wir untersuchen hier zunächst eine Ausschlagbrücke im unbelasteten Zustand: Dieser Fall liegt vor, wenn der Widerstand R 5 sehr groß ist, also „kein“ bzw. ein vernachlässigbarer „Querstrom“ I 5 fließt. Diese Annahme ist realistisch, wenn wir die Brückenspannung mit einem hochohmigen Digitalvoltmeter messen (Innenwiderstand des Voltmeters » 10 MW ). Wir betrachten kleine Änderungen des Widerstands R 1 und nehmen an, dass sich dieser Widerstand zusammensetzt aus einem festen (Anfangs-) Wert R 10 und der Änderung DR 1 . Dann ist uuu R 1 = R 10 + DR 1 . 5 Grundlagen Elektrotechnik I Laborversuch I-2.0 Wir nehmen weiterhin an, dass die Brücke vor Beginn des Experiments für R 1 = R 10 bzw. für DR 1 = 0 abgeglichen wurde. Dann ist die bereits bekannte Abgleichbedingung gegeben als uuu R 10 R 3 = , R2 R4 und für die Brückenspannung erhalten wir jetzt uuu é R2 R4 ù DU = ê úU . ë (R 10 + DR 1 ) + R 2 R 3 + R 4 û Diese Gleichung ist zwar exakt, aber wenig aussagekräftig. ¢ Aufgabe (Vorbereitung): ¢ ¢ ¢ ¢ Betrachten Sie diese Gleichung, und machen Sie sich zunächst unbedingt klar, dass ¢ ¢ ¢ die Brückenspannung im Fall DR = 0 verschwindet. 1 ¢ ¢ Üblicherweise werden kleine Widerstandsänderungen DR 1 gemessen. In diesem Fall kann man die oben stehende Gleichung durch eine wesentlich einfachere und übersichtlichere Gleichung ersetzen. Im weiteren Verlauf der Rechnung führen wir die Versorgungsspannung U der Brücke auf der linken Seite mit (Division durch U). Das ist bequemer. Im Nenner des ersten Bruches auf der rechten Seite klammern wir R 10 + R 2 aus und erhalten: DU = U R2 R4 é DR 1 ù R 3 + R 4 (R 10 + R 2 ) ê1 + ú ë R 10 + R 2 û Ist DR 1 sehr klein gegenüber R 10 + R 2 , dann ist auch der Quotient DR 1 sehr klein. In R 10 + R 2 1 » 1 - x (Anhang A2) anwenden, die für 1+ x DR 1 : „hinreichend kleine x“ gut erfüllt ist. An die Stelle von x tritt nun R 10 + R 2 diesem Fall dürfen wir die Näherungsformel DR 1 1 » 1, DR 1 R 10 + R 2 1+ R 10 + R 2 6 Grundlagen Elektrotechnik I Laborversuch I-2.0 so dass wir insgesamt erhalten: R2 é R4 DR 1 ù DU » ê1 úU R 10 + R 2 ë R 10 + R 2 û R 3 + R 4 Ausmultiplizieren liefert R2 R4 R2 DU » DR 1 . U R 10 + R 2 R 3 + R 4 (R 10 + R 2 ) 2 144424443 0 Da wir gefordert haben, dass die Brücke für R 1 = R 10 abgeglichen ist, verschwinden die ersten beiden Terme. Machen Sie sich das unbedingt klar. Es bleibt also R2 DU »DR 1 U (R 10 + R 2 ) 2 uuu Im Rahmen unserer Näherung ist die Brückenspannung also unmittelbar proportional zur Widerstandsänderung DR 1 ! Wie empfindlich DU auf DR 1 reagiert, hängt ab von der Versorgungsspannung U und von den Widerstandswerten R 10 und R 2 . Dabei ist R 10 in der Regel vorgegeben: Beispielsweise ist bei einer Temperaturmessung mit einem Platinfühler „Pt 100“ R 10 = 100 W bei T=0 C°. Prinzipiell erhalten wir einen großen Messeffekt, wenn wir die Spannung U groß wählen. ¢ ¢ ¢ ¢ ¢ ¢ ¢ ¢ Warum kann U nicht ohne Bedenken möglichst groß gewählt werden? Beantworten ¢ Sie diese Frage insbesondere auch im Hinblick auf die Temperaturmessung mit einem ¢ ¢ Widerstandsthermometer. ¢ Aufgabe (Vorbereitung): 0,20 R 10 =2 k W f(R 2) 0,15 0,10 0,05 0,00 0 2 4 6 8 10 Auf der Suche nach einem geeigneten Wert für R 2 ergibt sich eine interessante Beobachtung. Nebenstehend finden R2 Sie den Vorfaktor für einen Widerstandswert (R 10 + R 2 ) 2 R 10 = 2 kW als Funktion f (R 2 ) dargestellt. R2 durchläuft ein Maximum bei Der Faktor (R 10 + R 2 ) 2 Gleichheit von R 2 und R 10 . R 2/k W 7 Grundlagen Elektrotechnik I Laborversuch I-2.0 ¢ Aufgabe (Vorbereitung): ¢ ¢ R2 für R 2 = R 10 ein Maximum hat. ¢ Zeigen Sie, dass f (R 2 ) = 2 ( R + R ) 10 2 ¢ ¢ ¢ ¢ ¢ ¢ Es ist mit R 2 = R 10 R 10 1 = . 2 (R 10 + R 10 ) 4 R 10 Die Brückenspannung ist mit R 2 = R 10 uuu 1 DR 1 DU . »U 4 R 10 Dieser lineare Zusammenhang gilt nur für hinreichend kleine DR 1 . Für größere Widerstandsänderungen muss die verwendete Näherungsformel um weitere Beiträge erweitert werden: 1 » 1 - x + x 2 m ... 1+ x (vgl. Anhang A2). ¢ ¢ ¢ ¢ ¢ ¢ ¢ ¢ ¢ ¢ ¢ ¢ ¢ ¢ DU Leiten Sie eine „verbesserte Gleichung“ für her, indem Sie auch den quadrati- ¢ U ¢ schen Beitrag berücksichtigen. Schreiben Sie die resultierende Gleichung für den Fall ¢ R 2 = R 10 auf, und schätzen Sie ab, ab welchem DR 1 die lineare Näherung mit einem ¢ ¢ Fehler von 5% behaftet ist. ¢ ¢ Können Sie diesen Befund später in Ihren Messergebnissen wiederfinden? ¢ Aufgabe (Vorbereitung für „Rechenfreaks“): 8 Grundlagen Elektrotechnik I Laborversuch I-2.0 1.3.2 Ausschlagbrücke im belasteten Zustand Ri R5 Uq U5 Im Fall eines endlichen Widerstands R 5 bleibt die Abgleichbedingung unverändert gültig. Allerdings ist nun die Berechnung der Brückenspannung im Fall der „verstimmten“ Brücke ( DR 1 > 0 ) deutlich aufwendiger. Wichtig ist die Betrachtung dieser Situation, wenn Anzeigeinstrumente mit nicht vernachlässigbar großem Innenwiderstand verwendet werden müssen. Der Strom durch den Widerstand R 5 kann berechnet werden, wenn man sich diesen Widerstand aus der Schaltung herausgelöst denkt und die verbleibende Schaltung als Ersatzspannungsquelle auffasst. Diese Ersatzspannungsquelle hat die Quellspannung uuu é R2 R4 ù Uq = ê úU ë R1 + R 2 R 3 + R 4 û und den Innenwiderstand uuu Ri = R 3R 4 R 1R 2 . + R1 + R 2 R 3 + R 4 Für den Strom I 5 durch R 5 folgt dann I5 = Uq Ri + R5 und daher für die Spannung uuu é R2 R4 ù R5 ê ú R 5Uq R1 + R 2 R 3 + R 4 û ë U DU º U 5 = R 5 I 5 = = R 1R 2 R 3R 4 Ri + R5 + + R5 R1 + R 2 R 3 + R 4 ¢ Aufgabe (Vorbereitung): ¢ ¢ Welche Gleichung ergibt sich für DU , wenn R ® ¥ ? 5 ¢ ¢ ¢ ¢ ¢ Man kann von der oben stehenden Gleichung ausgehend genauso verfahren wie im Fall der unbelasteten Ausschlagbrücke und insbesondere für kleine DR 1 einen linearen Zusammenhang zwischen DU und DR 1 formulieren. Diese Vorgehensweise ist hier jedoch aufwendiger. Sie finden sie im Anhang A3 ausführlich dargestellt. Lassen Sie sich bitte nicht erschrecken! 9 Grundlagen Elektrotechnik I Laborversuch I-2.0 Für hinreichend kleine DR 1 findet man uuu é R 10 R 2 (R 10 + R 2 + R 3 ) + R 22 R 3 1 ù R2 DU R »D 1 ê1 ú, 2 U (R 10 + R 2 ) 2 ( R R ) R + 10 2 5û ë und setzt man wieder R 2 = R 10 so folgt: uuu DR 1 DU »U 4R 10 é R 10 + R 3 1 ù ê1 ú. 2 R5 û ë ¢ Aufgabe (Vorbereitung): ¢ ¢ Welche Gleichungen ergeben sich hier für DU , wenn R ® ¥ ? Wie sollte R 5 3 ¢ ¢ gewählt werden? Und R 4 ? ¢ ¢ ¢ ¢ ¢ 2 Laborversuche 2.1 Allgemeines ¢ ¢ ¢ ¢ ¢ ¢ ¢ ¢ Weisen Sie für alle Schaltungen, die von Ihnen aufgebaut und untersucht werden, ¢ nach, dass die beteiligten Bauteile und Geräte (hier insbesondere: Widerstände, ¢ ¢ Potentiometer, Widerstandsdekade) nicht überlastet werden. ¢ Aufgabe (Vorbereitung, Labor): Machen Sie sich vor der Versuchsdurchführung unbedingt mit der Funktionsweise der Widerstandsdekade vertraut! 2.2 Experiment: Abgleichbrücke Bauen Sie aus den Ihnen zur Verfügung stehenden Geräten und Zubehör eine Abgleichbrücke auf. Skizze! Verwenden Sie als Referenzwiderstände R 2 die Widerstandsdekade. Als „unbekannten Widerstand“ R 1 verwenden Sie einen Widerstand des Stecksystems (Experimentierbrett). Messen Sie mit der Brücke 5 Widerstände R 1 Ihrer Wahl (siehe auch 2.2) aus. Führen Sie für jeden einzelnen unbekannten Widerstand den Abgleich mit 5 verschiedenen Referenzwiderständen R 2 durch, so dass Sie das komplette Skalenspektrum 0 < x < 1 abdecken. 10 Grundlagen Elektrotechnik I Laborversuch I-2.0 Beachten Sie unbedingt die maximale Belastbarkeit der Widerstände. Führen Sie für jede Einzelmessung eine Fehlerabschätzung durch. 2.3 Experiment: Ausschlagbrücke ohne Belastung Bauen Sie aus den Ihnen zur Verfügung stehenden Geräten und Zubehör eine Ausschlagbrücke auf. Skizze! Verwenden Sie als R 10 und R 2 Widerstände, deren Werte sie zuvor mit der Abgleichbrücke ermittelt haben. Um einen veränderlichen Widerstand R 1 zu erhalten, schalten Sie R 10 in Reihe mit der Widerstandsdekade. Die dort eingestellten Werte repräsentieren dann die Widerstandsänderungen DR 1 . Vor Beginn der eigentlichen Messung wird im Fall DR 1 = 0 (alle Widerstände der Dekade „ausgeschaltet“) die Brücke am Präzisionspotentiometer möglichst genau abgeglichen. Dann beginnt die Messung: Sie variieren DR 1 und ermitteln die dazugehörigen Brückenspannungen DU . Ist der Zusammenhang linear? Ab wann treten in der grafischen Darstellung die ersten sichtbaren Abweichungen vom linearen Verhalten auf? Messen Sie in jedem Fall so weit, dass Sie eine deutliche Krümmung der Kurve beobachten können? Stimmen Experiment und Theorie für den linearen Bereich überein? Versuchen Sie mit Hilfe von Anhang A4 die Koeffizienten a 0 , a 1 , a 2 der quadratischen Funktion DU = a 0 + a 1 DR 1 + a 2 ( DR 1 ) 2 zu bestimmen. Führen Sie die beschriebene Prozedur für die folgenden drei Situationen durch: R 2 @ R 10 , R 2 < R 10 , R 2 > R 10 2.4 Experiment: Ausschlagbrücke mit Belastung Wiederholen Sie die unter 2.3 beschriebene Prozedur. Schalten Sie parallel zum Voltmeter nun aber einen Widerstand R 5 , der nicht zu klein gewählt werden sollte. Wird er zu groß gewählt, werden Sie jedoch keine Abweichungen von den bereits durchgeführten Messungen beobachten. (Richtwert 50 kW, vergleiche mit theoretischer Vorhersage, Abschnitt 1.3.2) 11 Grundlagen Elektrotechnik I Laborversuch I-2.0 Anhang A1 Fehlerbetrachtung Ist ein Messergebnis eine Funktion y = F( x 1 , x 2 ,..., x n ) einer oder mehrerer Messgrößen x1 , x 2 , ..., x n , so ist der Fehler des Messergebnisses nach dem Fehlerfortpflanzungsgesetz zu ermitteln. Die Fehlerfortpflanzung ist für die erfassten systematischen Fehler anders zu behandeln, als für zufällige Fehler. Fehlerfortpflanzung für systematische Fehler: Der systematische Fehler Dy einer Funktion y = F( x 1 , x 2 ,..., x n ) ist aus den systematischen Fehlern Dx 1 , Dx 2 , ..., Dx n der Einzelgrößen x1 , x 2 , ..., x n zu berechnen gemäß uuu Dy = å i ¶F ¶F ¶F ¶F Dx i = Dx 1 + Dx 2 + ... + Dx n . ¶x i ¶x 1 ¶x 2 ¶x n Es handelt sich bei dieser Gleichung im Prinzip um das totale Differential der Funktion F. Es wird angenommen, dass die Fehler Dx 1 , Dx 2 , ..., Dx n hinreichend klein sind, so dass eine Linearisierung der Funktion F angemessen ist. ¶F werden die eigentlichen Messgrößen ¶x i In die Ausdrücke für die partiellen Ableitungen eingesetzt. Die Vorzeichen der Ableitungen sind hier unbedingt zu beachten: Es kann also durchaus vorkommen, dass sich zwei in entgegengesetzter Richtung wirkende Fehlerbeiträge kompensieren. Fehlerfortpflanzung für zufällige Fehler: Der zufällige Fehler Dy einer Funktion y = F( x 1 , x 2 ,..., x n ) ist aus den zufälligen Fehlern Dx 1 , Dx 2 , ..., Dx n der Einzelgrößen x1 , x 2 , ..., x n zu berechnen gemäß 2 uuu 2 2 2 é ¶F ù ù é ¶F ù é ¶F é ¶F ù Dx n ú . Dx 2 ú + ... + ê Dx 1 ú + ê Dy = å ê Dx i ú = ê i ë ¶x i ë ¶x n û û ë ¶x1 û ë ¶x 2 û ¶F werden die eigentlichen Messgrößen ¶x i eingesetzt, Dx 1 , Dx 2 , ..., Dx n sind die geschätzten Fehler. In die Ausdrücke für die partiellen Ableitungen 12 Grundlagen Elektrotechnik I Laborversuch I-2.0 (Liegen für jede Einzelgröße mehrere Messergebnisse vor, so setzt man in die partiellen Ableitungen die Mittelwerte x1 , x 2 , ..., x n ein und für Dx 1 , Dx 2 , ..., Dx n die Standardabweichungen.) Mit uuu 1 ¶F 1 ¶F é1 ù = -1 , = -R 2 2 R 1 = F(R 2 , x ) = R 2 ê - 1ú und ¶R 2 x ¶x x ëx û folgt 2 é1 ù R 22 2 DR 1 = ê - 1ú (DR 2 ) + 4 (Dx ) 2 . x ëx û Der relative Fehler von R 1 ist dann DR 1 = R1 2 é1 ù R 22 1 2 - 1ú (DR 2 ) + 4 (Dx ) 2 ê x é1 ù x û R 2 ê - 1ú ë ëx û und kompakter uuu DR 1 ( DR 2 ) 2 (Dx ) 2 = + 2 R1 R 22 x (1 - x ) 2 Lassen wir einmal den Fehlerbeitrag des (im Normalfall hochpräzisen) Referenzwiderstands außer acht, so bleibt der diskussionswürdige Fehlerbeitrag uuu DR 1 Dx = R1 x (1 - x ) 2,0 Dx=0.001 1,5 DR 1 / R 1 * 100% ¢ Aufgabe (Vorbereitung): ¢ ¢ ¢ ¢ Wie sollte man den Referenzwiderstand wählen, um ¢ ¢ optimale Mesergebnisse zu erzielen? Erklärung? ¢ ¢ ¢ 1,0 0,5 0,0 0,0 0,2 0,4 0,6 x 13 0,8 1,0 Grundlagen Elektrotechnik I Laborversuch I-2.0 A2 Potenzreihenentwicklung von Funktionen: Linearisierung Häufig ist es zweckmäßig, Funktionen f ( x ) in der Nähe eines bestimmten Wertes x = x 0 durch einfachere Funktionen (hier: Polynome) anzunähern bzw. zu ersetzen. Den Wert x = x 0 nennt man Entwicklungspunkt. Unter gewissen Voraussetzungen kann man die Annäherung durch Polynome durch Berücksichtigung (unendlich) vieler Glieder beliebig genau machen. In der Praxis ist man aber meist an möglichst einfachen „Ersatzfunktionen“ interessiert. Die unten allgemein darstellte sogenannte MacLaurinsche Reihe ( x 0 = 0 ) wird daher nach wenigen Gliedern abgebrochen: uuu 1 1 1 f ( x ) » f (0) + f ¢(0) x + f ¢¢(0) x 2 + f ¢¢¢(0) x 2 + .... = å f ( k ) (0) x k 2 6 k = 0 k! wobei mit f ( k ) (0) die k-te Ableitung der Funktion f(x) an der Stelle x = 0 gemeint ist. Dabei ist die „nullte Ableitung“ f ( 0) (0) = f (0) , also die Funktion selbst. Will man die „Originalfunktion“ durch eine Gerade annähern, so benötigt man nur die ersten beiden Glieder der Reihe: f ( x ) » f (0) + f ¢(0) x Geometrisch interpretiert bedeutete dies: Die Funktion f ( x ) wird an der Stelle x 0 = 0 durch eine Tangente, also durch eine Gerade ersetzt. Im Zusammenhang mit diesem Laborversuch interessiert besonders die Funktion f (x) = 1 1+ x mit den Ableitungen f ¢( x ) = - 1 , (1 + x ) 2 f ¢¢( x ) = 2 , (1 + x ) 3 f ¢¢¢( x ) = - 6 etc. (1 + x ) 4 und damit f ( 0) = 1 , f ¢(0) = -1 , f ¢¢(0) = 2 , f ¢¢¢(0) = - 1 etc.. 6 1 1 Setzt man diese Werte in f ( x ) » f (0) + f ¢(0) x + f ¢¢(0) x 2 + f ¢¢¢(0) x 2 + .... ein, so folgt 2 6 uuu 1 @ 1 - x + x 2 - x 3 ± ... 1+ x 14 Grundlagen Elektrotechnik I Laborversuch I-2.0 Diese und andere Reihenentwicklungen häufig verwendeter Funktionen findet man in Formelsammlungen zusammengestellt. Die folgenden Abbildungen sagen Ihnen vermutlich mehr als tausend Worte: 2,0 1,5 1,5 1,0 y y 1,0 0,5 0,0 -1 0 1 2 3 0,5 -0,50 4 -0,25 x f (x) = 0,00 0,25 0,50 x 1 und 1 - x 1+ x wie links, anderer Maßstab 1,5 2,0 1,5 1,0 y y 1,0 0,5 0,5 -0,50 0,0 -1 0 1 2 3 4 f (x) = 1 , 1 - x + x 2 und 1 - x + x 2 - x 3 1+ x 0,00 0,25 0,50 wie links, anderer Maßstab In der Praxis hat man häufig Ausdrücke der Form müssen: 1 1 1 = x a+x a 1+ a An die Stelle von x in -0,25 x x 1 x tritt nun : 1+ x a 15 1 , die zunächst umgeformt werden a+x Grundlagen Elektrotechnik I 1 1+ x a @ 1- Laborversuch I-2.0 x x2 x3 + - ± ... , a a2 a3 so dass insgesamt 1 1 1 1 x x 2 x3 = @ - 2 + 3 - 4 ± ... a + x a 1+ x a a a a a uuu A3 Linearisierung der Brückenspannung im belasteten Fall Häufig finden Sie in Lehrbüchern die Formulierung „Wie man leicht zeigen kann ...“ Seien Sie misstrauisch, wenn Ihnen eine solche Floskel begegnet. In der Regel kommt man nämlich nicht aus eigener Kraft zum gewünschten Ergebnis. So ist das sicher auch im vorliegenden Fall. Vielleicht wollen Sie aber trotzdem einmal versuchen, den Rechenweg nachzuvollziehen. Viel Spaß! Wir starten mit uuu é R2 R4 ù R5 ê ú R 5Uq R1 + R 2 R 3 + R 4 û ë U, DU = = R 1R 2 R 3R 4 Ri + R5 + + R5 R1 + R 2 R 3 + R 4 eliminieren die Doppelbrüche und klammern im Nenner R 1 aus: R 5 ( R 2 R 3 - R 1R 4 ) DU = U R 1{R 2 (R 3 + R 4 ) + R 3 R 4 + (R 3 + R 4 )R 5 } + R 2 R 3 R 4 + (R 3 + R 4 )R 2 R 5 Mit R 1 = R 10 + DR 1 erhalten wir R 5 {R 2 R 3 - (R 10 + DR 1 )R 4 } DU = U (R 10 + DR 1 ){R 2 (R 3 + R 4 ) + R 3 R 4 + (R 3 + R 4 )R 5 } + R 2 R 3 R 4 + (R 3 + R 4 )R 2 R 5 Nach einer Umformung des Zählers zeigt sich, wie dort die Abgleichbedingung eingearbeitet werden kann: 0 6447 44 8 R 5 (R 2 R 3 - R 10 R 4 - R 4 DR 1 ) DU = . U (R 10 + DR 1 ){R 2 (R 3 + R 4 ) + R 3 R 4 + (R 3 + R 4 )R 5 } + R 2 R 3 R 4 + (R 3 + R 4 )R 2 R 5 16 Grundlagen Elektrotechnik I Laborversuch I-2.0 Dann bleibt zunächst - R 4 R 5 DR 1 DU = U (R 10 + DR 1 ){R 2 (R 3 + R 4 ) + R 3 R 4 + (R 3 + R 4 )R 5 } + R 2 R 3 R 4 + (R 3 + R 4 )R 2 R 5 Nun werden Zähler und Nenner durch R 4 dividiert: DU = U - R 5 DR 1 R3 R R (R 10 + DR 1 ){R 2 ( + 1) + R 3 + ( 3 + 1)R 5 } + R 2 R 3 + ( 3 + 1)R 2 R 5 R4 R4 R4 Im Nenner ersetzen wir dann DU = U R3 R durch 10 (Abgleichbedingung): R4 R2 - R 5 DR 1 R R R (R 10 + DR 1 ){R 2 ( 10 + 1) + R 3 + ( 10 + 1)R 5 } + R 2 R 3 + ( 10 + 1)R 2 R 5 14243 R2 R2 R2 » R10 Für kleine DR 1 ist R 10 + DR 1 » R 10 und damit DU = U - R 5 DR 1 R R R 10 {R 10 + R 2 + R 3 + ( 10 + 1)R 5 } + R 2 R 3 + ( 10 + 1)R 2 R 5 R2 R2 . Nun wird der Nenner so umgeformt, dass R 5 nur einmal erscheint: DU = U - R 5 DR 1 R 10 {R 10 + R 2 + R 3 } + R 2 R 3 + ( R 10 + 1)(R 10 + R 2 )R 5 R2 Mit ( (R + R 2 ) 2 R 10 + 1)(R 10 + R 2 ) = 10 R2 R2 und Kürzen mit R 5 haben wir dann - DR 1 DU = 2 U (R 10 + R 2 ) R (R + R 2 + R 3 ) + R 2 R 3 + 10 10 R2 R5 17 Grundlagen Elektrotechnik I (R 10 + R 2 ) 2 aus und erhalten R2 Wir klammern DU = U Laborversuch I-2.0 - DR 1 é ù ê ú (R 10 + R 2 ) ê R 10 (R 10 + R 2 + R 3 ) + R 2 R 3 ú 1+ ê ú (R 10 + R 2 ) 2 R2 R 5 ê ú R2 ë û 2 - R 2 DR 1 DU = U (R 10 + R 2 ) 2 1 R R (R + R 2 + R 3 ) + R 22 R 3 1 1 + 10 2 10 (R 10 + R 2 ) 2 R5 Für hinreichend große R 5 verwenden wir wieder uuu 1 » 1 - x und erhalten 1+ x é R 10 R 2 (R 10 + R 2 + R 3 ) + R 22 R 3 1 ù R2 DU »DR 1 ê1 ú. (R 10 + R 2 ) 2 R5 û U (R 10 + R 2 ) 2 ë Das war es! Vielleicht kommt man auch einfacher zu diesem Ergebnis. Entsprechende Tipps werden dankbar entgegengenommen!!! A4 Ausgleichsrechnung, Regressionsanalyse Wollen Sie statt einer Geraden (Laborversuch I-1.0) eine Parabel an einen Messwertesatz „anfitten“, so gehen Sie aus von der allgemeinen Gleichung uuu y = f (x) = a 0 + a1x + a 2 x 2 Die Parameter a 0 , a 1 , a 2 sind so zu bestimmen, dass für Ihren Datensatz ( x i , y i ) mit i = 1, ..., n die Summe der Fehlerquadrate minimal wird (Methode der kleinsten Fehlerquadrate). Die Fehler sind y i - a 0 - a 1x - a 2 x 2 , die quadrierten Fehler sind dann ( y i - a 0 - a 1 x - a 2 x 2 ) 2 . Für die Summe der Fehlerquadrate erhalten wir S = ( y1 - a 0 - a 1 x 1 - a 2 x 12 ) 2 + ( y 2 - a 0 - a 1 x 2 - a 2 x 22 ) 2 + ... + ( y n - a 0 - a 1 x n - a 2 x 2n ) 2 oder kompakter uuu n S(a 0 , a 1 , a 2 ) = å ( y i - a 0 - a 1 x i - a 2 x i2 ) 2 . i =1 18 Grundlagen Elektrotechnik I Laborversuch I-2.0 Die Fehlerquadratsumme ist also eine Funktion der unabhängigen Variablen a 0 , a 1 , a 2 . Das Minimum dieser Funktion ergibt sich im Fall verschwindender partieller Ableitungen: ¶S =0, ¶a 0 ¶S = 0, ¶a 1 ¶S =0 ¶a 2 Diese Bedingungen führen auf ein lineares Gleichungssystem für a 0 , a 1 , a 2 : é ê n ê n ê x i êå i =1 ên êå x i2 ëê i=1 é n ù ù ê å yi ú ú i =1 ú ú éa 0 ù ê ni=1 n ú 3ú ê ê x i × ê a1 ú = å x i yi ú , å ê i=1 ú ú i =1 n ú ú êëa 2 úû ê n 4 2 ê ú x x y å å i i úûú i i =1 ëê i =1 ûú n n åx åx i i =1 n åx 2 i åx 3 i i =1 n i =1 2 i das am besten mit dem PC oder Taschenrechner gelöst wird. Viele Taschenrechner lösen sogar das komplette Ausgleichsproblem. Rechenschema: Mit dem folgenden Schema können Sie die Elemente der Koeffizientenmatrix und der rechten Seite des Gleichungssystems ermitteln: i 1 2 M n xi yi x i2 n å i =1 19 x 3i x i4 x i yi x i y i2