Handout: Atommodelle - Demokrit, Dalton, Thomson, Rutherford und

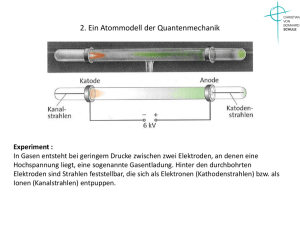
Handout: Atommodelle - Demokrit, Dalton, Thomson, Rutherford und Bohr.
Bis heute gab es immer wieder neue Atommodelle, da die bestehenden neuen physikalischen Erkenntnissen nicht
mehr genügten.
Demokrit (460-371 v. Chr.)
John Dalton (1766-1844)
Englischer Physiker und Chemiker
Bereits Demokrits Lehrer Leukipp sagte, dass Stoffe aus kleinsten Teilen bestehen. Demokrit erweiterte dieses Modell: Er sagte, dass sich die Atome im
leeren Raum frei bewegen können, zusammenstoßen, sich vereinigen und wieder trennen. Weiterhin gebe es nur die Atome und den leeren Raum.
Mit Hilfe aus der Chemie bekannten Gesetzmäßigkeiten entwickelte Dalton eine genauere (und auf Experimenten basierende) Vorstellung von den Atomen:
• Jedes Element bestehe aus charakteristischen, untereinander gleichen
und unteilbaren Atomen.
• Atome unterscheiden sich nur in der Masse von Atomen anderer Elemente.
Joseph John Thomson (1856-1940)
Brtischer Physiker, Nobelpreis 1906
Mit diesem Modell ließen aber noch nicht elektrische Leitungsvorgänge z.B.
in Gasen bzw. die Ladung von Atomen erklären.
1897 bewies Thomson, dass Katodenstrahlen aus geladenen Teilchen bestehen. Bei den geladenen Teilchen, die bei der Gasentladung entstanden sind,
handelte es sich um positive Ionen (charakteristischer mq -Wert) und negative
Elekronen (immer gleicher Quotient mq ).
→ Elektronen sind Bestandteile aller Atome.
Thomson’sches Atommodell (Rosinenkuchenmodell): Ein Atom besteht
aus einer gleichmäßig positiv geladenen Materiekugel, in der die Elektronen
regelmäßig verteilt eingebettet sind.
Rutherford’scher Streuversuch
Rutherford beschoss eine Goldfolie mit α-Strahlung und maximalen potentiellen Energie gleich (beim Zusammenbeobachte die Ablenkung der α-Teilchen, was zu den fol- treffen von Teilchen und Kern geht die die kin. in pot.
genden Ergebnissen führte:
Energie über).
1. Fast alle α-Teilchen gehen ohne Ablenkung durch
die Folie hindurch.
1 2
1
Ze
mv =
·
· 2e
2
4πε0 r
Ze
2
r=
·
· 2e
4πε0 mv2
2. Einige α-Teilchen werden in alle Richtungen abgelenkt. Kleinere Ablenkwinkel kommen dabei häufiger, große selten vor.
Damit ergibt sich ein Atomkern-Durchmesser von
Ablenkungen von 180° zeigen, dass die Masse der α- 10−14 m.
Teilchen kleiner ist, als die mit der sie zusammengestoßen
sind. Somit scheiden die leichten Elektronen als Streuzen- Außerdem gilt für das Rutherford’sche Atommodell:
• Die Hülle des Atoms besteht aus negativen Laduntrum aus.
gen.
Rutherford kam zu dem Schluss, dass die Masse im Atom
• Der Atomkern besteht aus positiven Ladungen.
nicht gleichmäßig verteilt ist (Widerspruch zu Thomson),
• Gesamtladung des Atoms ist neutral.
sondern dass es einen positiv geladenen Atomkern und ei• Der Raum zwischen dem Kern und der Atomhülle
ne negative Atomhülle gibt.
ist leer.
Die Größe des Atomkerns lässt sich bestimmen. Dazu
•
Atome
haben einen Durchmesser von ca. 10−10 m.
setzt man die kinetische Energie der α-Teilchen mit der
1
Widersprüche und Probleme des Rutherford’schen Atommodells:
• Atom wäre nicht stabil. Das Elektron müsste in den Kern stürzen.
• Gesamtenergie ist nicht diskret.
• Quantenhafte Emission und Absorption von Energie ist nicht erklärbar.
Das Bohr’sche Atommodell
Bohr löste 1913 die Probleme des Rutherford’schen Atommodells indem er Erkenntnisse aus der Quantentheorie auf
das Atom übertrug. Seine Theorie wird durch die Bohr’schen Postulate beschrieben, die allerdings nur auf Wassterstoff
und wasserstoffähnliche Atome anzuwenden sind.
1. Bohr’sches Postulat (Quantenbedingung)
Die Elektronen des Atoms bewegen sich nur auf bestimmten stabilen Kreisbahnen um den Atomkern und geben dabei
keine Energie in Form von elekromagnetischer Strahlung ab. Der Bahndrehimpuls L nimmt dabei nur Vielfache von
h
2π an.
L = r·m·v = n·
h
2π
n ∈ N∗
n ist die Quantenzahl und gibt die Bahn an,
in der sich das Elektron befindet.
2. Bohr’sches Postulat (Frequenzbedingung)
Geht ein Elektron von einer Bahn mit hoher Energie (großes n) zu einer Bahn mit geringerer Energie über, wird die
Differenz der Energien als Photon abgegeben (Emission).
E ph = h · f = Em − En = ∆E
m, n ∈ N∗ , m > n
Beim umgekehrten Vorgang wird ein Photon aufgenommen (Absorption).
Berechnung der diskreten Energiezustände des Wasserstoffatoms
Man hat festgestellt, dass das Energiespektrum des Wasserstoffs aus diskreten Linien besteht. Mit Bohrs Theorie
lassen sich diese Zustände erklären und auch die Energien berechnen.
Die diskreten Werte entstehen durch Aufnahme bzw. Abgabe von Photonen, deren Energie abhängig von den Bahnen
des Elektrons ist (→2. Postulat).
Berechnung der Energie eines Elektrons auf einer Bahn:
Die Gesamtenergie auf der n-ten Bahn beträgt
En = Ekin,n + E pot,n .
Da es sich um Wasserstoff (1 Proton im Kern, 1 Elektron)
handelt gilt Q1 = −Q2 = −e. Eingesetzt führt das zu folgender Gleichung, die nur den Radius der Kreisbahn rn
als Unbekannte enthält.
Für die kinetische Energie gilt folgende Formel bei der
e2
die Geschwindigkeit der Elektronen auf der n-ten Bahn
E pot,n = −
unbekannt ist.
4πε0 rn
1
2
Ekin,n = me vn
Nun müssen der Radius der Kreisbahn (Abstand des Elek2
Die potentielle Energie ergibt sich aus dem Co- trons zum Kern) und die Geschwindigkeit bestimmt werloumb’schen Gesetz und ist abhängig vom Abstand rn des den.
Elektrons zum Atomkern.
E pot,n =
Q1 · Q2
1
·
4πε0
rn
2
Bahn in der sich das Elektron befindet abhängig ist.
Radius und Geschwindigkeit:
Da sich das Elektron auf einer Kreisbahn bewegt, muss es (2) eingesetzt in die Formel für die kinetische Energie lieeine Zentripetalkraft erfahren. Diese liefert die Coloumb- fert:
kraft.
e4
1
m e e4
Ekin,n = me 2 2 2 = 2 2 2
2 4ε0 h n
8ε0 h n
FZ = FC
Die potentielle Energie ist ebenso diskret, da diese nur
me · v2
e2
=
von rn abhängig ist. (3) eingesetzt in die Formel für die
2
r
4πε0 r
potentielle Energie ergibt:
e2
(1)
rme v2 =
4πε0
m e e4
E pot,n = − 2 2 2
Nun kann mit Hilfe des 1. Postulates die Geschwindigkeit
4ε0 h n
vn bestimmt werden.
Für die Gesamtenergie auf der n-ten Bahn ergibt sich
n·h
schließlich:
rn me vn =
= L |·vn
2π
L · vn = rn me v2n |(1) einsetzen
En = Ekin,n + E pot,n
2
e
1 me e4
1 me e4
=
=
−
2
4πε0
8 ε0 h2 n2 4 ε02 h2 n2
n·h
e2
· vn =
1 me e4 1
2π
4πε0
E
=
−
n
8 ε02 h2 n2
e2
vn =
(2)
2nhε0
Allein die Quantenzahl n bestimmt also den EnergiezuMit der nun bestimmten Geschwindigkeit lässt sich auch stand des Atoms. Im Grundzustand n = 1 gilt:
der Radius rn bestimmen. Dazu wird (2) in (1) eingesetzt
E1 = −2, 18 · 10−18 J = −13, 6 eV
und es ergibt sich:
rn =
h2 ε0
· n2
πme e2
Damit lässt sich die Energie in allen anderen Zuständen
(3) berechnen:
1
1
Es ergeben sich gemäß des 1. Postulates nur ganz beEn = E1 2
En = −13, 6 eV · 2
n
n
stimmte feste Radien bzw. Bahnen. Der Radius ist abhängig von der Bahn n, in der sich das Elektron bewegt. Für Trägt man entlang einer Energieachse die Gesamtenergie
n = 1 gilt r1 = 5, 29 · 10−11 m (Bohr’scher Radius).
En des Elektrons für n = 1, 2, 3, . . . auf, so erhält man das
Energieniveauschema des Wasserstoffatoms.
Diskrete Energiewerte:
Die kinetische Energie ist diskret, da sie nur von vn abhängig ist, was wiederum von der Quantenzahl n bzw. der
3