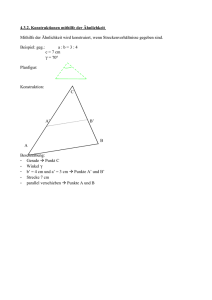
Hilbert Ebene

Hilbert Ebene Letzte Woche wurden uns die Axiome von Hilbert vorgestellt, genauer gesagt haben wir
gesehen:
-
die Axiome der Verknüpfungen (Axioms of Incidence)
die Axiome der Anordnung (Axioms of Betweeness) sowie
die Axiome der Kongruenz von Strecken und Winkel
Nun werden wir heute in einem ersten Schritt die Hilbert Ebene definieren und dann
aufzeigen wie viel von Euklids Buch 1 in der Hilbert Ebene abgedeckt werden kann (zwei
Ausnahmen die ausgeschlossen werden da diese mit dem Parallelaxiom in Berührung
kommen).
Dabei ist vorwegzunehmen dass das Parallelaxiom in dieser Betrachtung nicht
miteinbezogen wird, weil die Axiome der Hilbert Ebene eine Basis sowohl für nicht
Euklidische (Geometrie in denen Parallelaxiom abgeändert oder gar gestrichen wurde wie
zb. die hyperbolische Geometrie die Lobatschewski aufgestellt hat) als auch für Euklidische
Geometrie bildet (aus diesem Grund nennt mancher die Hilbert Ebene auch die neutrale
Geometrie).
Definition (Hilbert Ebene)
Eine Hilbert Ebene ist eine Menge (von Punkten) zusammen mit bestimmten Teilmengen,
den Linien (sowie den undefinierten Begriffen der Anordnung, der Kongruenz für Strecken
wie auch der Kongruenzen für Winkel) welche die Axiome (I1)-(I3), (B1)-(B4), und (C1)-(C6)
erfüllen.
Wir werden nun wie bereits gesagt die Propositionen von Euklid (Buch 1) Schritt für Schritt
durchgehen und schauen wie wir diese in Hilberts Ebene abdecken können.
Proposition (I.1)
(„Über einer gegebenen Strecke ein gleichseitiges Dreieck zu errichten“)
Ist unsere erste Ausnahme. Ohne zusätzliche Axiome ist nicht klar, dass sich die zwei Kreise
in Euklids Konstruktion auch kreuzen.
Tatsächlich folgt die Existenz eines gleichseitigen Dreiecks auf gegebener Strecke nicht aus
Hilberts Axiomen (Werden wir später noch sehen Exercise 39.31). Wir wollen diese Lücke
jedoch mithilfe der Existenz eines gleichschenkligen Dreiecks füllen. Diese Existenz werden
wir später zeigen (Proposition 10.2)
Proposition (I.2)/(I.3)
(„Wie von einem Punkt D aus eine Strecke DW gezeichnet wird die gleich lang ist wie die
gegebene Strecke AB“ / „Wie auf einer gegebenen Strecke DE eine Strecke abgetragen
werden kann, die in einem Punkt Z beginnt und genauso lang sein soll wie eine gegebene
Strecke AB“)
Werden ersetzt durch das Axiom (C1) (Transportieren von Strecken)
Proposition (I.4) (SAS: Sides Angel Sides)
(„Wenn in zwei Dreiecken zwei Seiten zwei Seiten entsprechend gleich sind und die von den
gleichen Seiten eingeschlossenen Winkel einander gleich, dann muss in ihnen auch die
Grundlinie der Grundlinie gleich sein, das Dreieck muss dem Dreieck gleich sein, und die
übrigen Winkel müssen den übrigen Winkeln entsprechend gleich sein, nämlich immer die ,
denen gleiche Seiten gegenüberliegen“)
Wird ersetzt durch das Axiom (C6)
Proposition (I.5)
(In einem gleichschenkligem Dreieck sind Basiswinkel kongruent)
Beweis von Euklid ist ok und kann so übernommen werden, d.h. in anderen Worten jeder
Beweisschritt kann mit der Struktur der Hilbert Ebene begründet werden. Wir betrachten nun
Euklids Beweis und schauen Schritt für Schritt wie das in der Hilbert Ebene übernommen
werden kann.
Beweis:
Sei ABC ein gegebenes gleichschenkliges Dreieck mit AB≅AC (kongruente Strecken). Wir
müssen nun zeigen dass dann die Basiswinkel ⦟ABC und ⦟ACB auch kongruent sind.
Nehme dazu auf BD beliebigen Punkt F (möglich dank Axiom (B2)). Auf AE trenne AG derart
ab so dass AG gleich AF (möglich dank Axiom (C1)).
Somit ist AC≅AB und AF≅AG und der eingeschlossene Winkel ⦟BAC ist noch immer der
gleiche. Somit mit (C6) müssen die Dreiecke AFC und AGB kongruent sein. Weiter muss
FC≅GB und ⦟AFC≅⦟AGB und ⦟ACF≅⦟ABG. Da gleiches subtrahiert von gleichem gleich
ist, können wir schließen (von 8.3) dass BF≅CG. Dann wieder mit (C6) sind die Dreiecke
FBC und GCB kongruent und es folgt dass ⦟CBG≅⦟BCF.
Vom Kapitel 9 von letzter Woche (Exercise 9.1) wissen wir nun dass durch Subtraktion von
kongruenten Winkeln die Winkel ⦟ABC und ⦟ACB kongruent sein müssen und somit gilt die
Behauptung.
In gewissen Beweisschritten benötigen wir Wissen in Bezug auf die Anordnung von Punkten,
was wir jedoch formal mit unseren Axiomen beweisen können. Zum Beispiel im Falle dass
man das Liniensegment AB von der Strecke AF abträgt, müssen wir wissen dass B zwischen
A und B liegt. Das folgt jedoch von der Wahl unseres F. Zum Schluss, wenn es um Winkel
geht, die abgetragen werden müssen, geht es darum zu wissen dass BC im Innern des
Winkels ⦟ABG liegt. Dies folg vom Fakt, dass C zwischen A und G liegt.
So zukünftig wenn wir sagen dass Euklids Beweis ok ist bedeutet das dass wir jeden
Beweisschritt mit Axiomen von Hilbert bzw mit den Resultaten die wir bekommen haben
begründen können.
Proposition (I.6) (Umkehrung von Proposition (I.5))
(Falls zwei Winkel in einem Dreieck gleich sind, dann sind auch die jeweiligen Gegenseiten
gleich)
Beweis ist ok außer einem Schritt am Ende von Euklids Beweis
Euklid benutzt bei seinem Widerspruchbeweises die Ungleichheit von zwei Dreiecke, was wir
in unserem System nicht abdecken können da wir Ungleichheit von Dreiecken nicht definiert
haben.
Abhilfe schafft hierbei ein kleiner Zusatz:
Denn von der Kongruenz der beiden Dreiecke DBC≅ACB (für Euklid ist diese Gleichheit
absurd) folgt dass die Winkel ⦟DCB≅⦟ABC und auch ⦟ABC≅⦟ACB gemäss Annahme.
Somit gilt dass auch Winkel ⦟DCB≅⦟ACB was jedoch ein Widerspruch zur Eindeutigkeit vom
Axiom (C4) darstellt, da nur ein Winkel auf der gleiche Seite von CB kongruent zum Winkel
⦟ACB sein kann.
Es folgt dass die Strecken CA und CD gleich sind, somit ist A=D und das Dreieck ist
gleichschenklig wie gewünscht.
Proposition (I.7)
Benötigt zusätzliche Begründungen bezüglich der Anordnung von Linien. In Exercise 9.4
definierten wir genau dieses fehlende Argument so dass wir Euklids Beweis übernehmen
können.
(Genauer gesagt falls wir annehmen dass die Strecke AD im Innern des Winkels CAB und
dass D ausserhalb des Dreiecks CAB liegt, dann müssen wir zeigen dass die Strecke CB
dann im Innern des Winkels ACD und die Strecke DA im Innern des Winkels CDB liegt).
Proposition (I.8) (SSS)
(„Wenn bei zwei Dreiecken sowohl die beiden Seiten kongruent sind wie auch die Basisseite,
dann sind auch entsprechende Winkel kongruent“)
Es existiert kein Axiom von Hilbert welches die „Überlagerung“ zweier Dreiecke in Euklids
Beweis definiert, deshalb benötigt diese Präposition einen neuen Beweis.
Proposition 10.1 (Beweis SSS)
Wenn für zwei Dreiecke ABC und A’B’C’ folgendes gilt: AB≅A’B’, AC≅A’C’ und BC≅B’C’,
dann sind die zwei Dreiecke kongruent
Beweis
Mit den Axiomen (C4) und (C1) konstruieren wir einen Winkel ⦟C’A’B’’ (auf A’C’ gegenüber
von B’) so dass dieser kongruent zu ⦟BAC ist und mache zusätzlich A’B’’ kongruent zu AB.
Dann ist durch Konstruktion AB≅A’B’’ und gemäss Annahme AC≅A’C’ und der Winkel
⦟BAC≅⦟B’’A’C’ durch Konstruktion. Mit (C6) ist dann das Dreieck ABC kongruent zum
Dreieck A’B’’C’ und es folgt dass BC≅B’’C’.
Zeichne nun die Linie B’B’’. Es folgt dass A’B’≅AB≅A’B’’ und mit der Transitivität gilt somit
dass A’B’≅A’B’’. Das Dreieck A’B’B’’ ist dann gleichschenklig und mit (I5) gilt dass deren
Basiswinkel ⦟A’B’B’’ und ⦟A’B’’B’ kongruent sind.
Das gleiche gilt für B’C’≅B’’C’, somit ist auch das Dreieck C’B’B’’ gleichschenklig und deren
Basiswinkel ⦟B’’B’C’ und ⦟B’B’’C’ sind kongruent. Durch Addition kongruenter Winkel folgt
(9.4) dass der Winkel ⦟A’B’C’≅⦟A’B’’C’
Da gezeigt wurde dass das Dreieck ABC kongruent zu A’B’’C’ ist gilt dass der Winkel
⦟A’B’’C’≅⦟ABC. Wieder gemäss der Transitivität der Kongruenz folgt dass der Winkel
⦟ABC≅⦟A’B’C’, mit dem Axiom (C6) folgt somit dass diese beiden Dreiecke kongruent sind.
Proposition I.9
(„Um einen gegebenen Winkel zu halbieren“)
Euklid braucht für die Beweisführung bei Proposition (I.9) eine Reihe von Konstruktionen (mit
Massstab und Zirkel) welche wir so in der Hilbert Ebene nicht ausführen können. Zudem
besitzen wir bis jetzt noch immer kein Axiom, welches uns versichert, dass Linien und Kreise
sich schneiden wenn dies verlangt wird. Wie auch immer, wir können diese Propositionen als
Existenztheoreme anschauen und diese dann mit den Hilbert Axiomen beweisen.
Da wir bis jetzt keine gleichseitigen Dreiecke haben die Euklid in (I.1) konstruiert hat, werden
wir die Existenz von gleichschenkligen Dreiecken zeigen und diese dann als Substitute für
gleichseitige Dreiecke benutzen um die Existenzbeweise durchzuführen.
Proposition 10.2 (Existenz von gleichschenkligen Dreiecken)
Für gegebene Strecke AB existiert ein gleichschenkliges Dreieck mit Basis AB
Beweis
Sei AB gegebene Strecke. Und sei C ein beliebiger Punkt welcher nicht auf AB liegt (Axiom
(I3)). Betrachte das Dreieck ABC. Falls die Winkel bei A und B gleich sind, dann ist das
Dreieck ABC bereits gleichschenklig (I.6). Falls nicht, ist einer der Winkel kleiner als der
andere, nehmen wir nun an es gilt Winkel ⦟CAB < ⦟CBA. Dann gibt es eine Strecke BE im
Inneren des Winkels ⦟CBA so dass der Winkel ⦟CAB≅⦟EBA. Mit dem Theorem 7.3 aus
letzter Woche (Crossbar Thm.: Winkel CBA gegeben und E ein Punkt im Innern des Winkels,
dann muss der Vektor BE die Strecke AC schneidet) wissen wir dass der Vektor BE die
Strecke AC in einem Punkt D schneidet. Somit sind die Basiswinkel des Dreiecks DAB
gleich und es folgt mit (I.6) dass das Dreieck gleichschenklig sein muss.
Bemerkung:
Es reicht nicht an den beiden Enden von AB zwei gleiche Winkel zu konstruieren, weil ohne
Parallelaxiom ist keine Garantie dass diese beiden Strecken sich treffen, egal wie klein die
Winkel auch sein mögen.
Proposition (I.9)
Nun zurück zu Euklid. Wir benutzen bei der Beweisführung die gleiche Methode wie Euklid,
nur dass wir die Proposition 10.2 brauchen um die Existenz eines gleichschenkligen
Dreiecks DEF zu definieren dort wo Euklid ein gleichseitiges Dreieck einsetzt.
Proposition (I.10)
(Um eine Gerade AB zu halbieren)
Um eine gegebene Strecke zu halbieren benutzen wir wieder 10.2 um ein gleichschenkliges
Dreieck anstelle eines gleichseitigen zu konstruieren. Der Rest des Beweises funktioniert
wiederum analog zum Beweis von Euklid (um zu zeigen dass ein Mittelpunkt eines
Segments existiert).
Proposition (I.11)
(Um einen Rechten Winkel zu zeichnen bei gegebener Linie AB und gegebenen Punkt D auf
AB)
Wir können wiederum 10.2 benutzen um das gleichseitige Dreieck aus Euklids Beweis mit
einem gleichseitigen zu ersetzen. Der Beweis folgt dann analog.
(Das beweist auch die Existenz eines Rechtwinkels)
Proposition (I.12)
(Um einen Rechten Winkel zu zeichnen bei gegebener Linie AB und gegebenen Punkt D
nicht auf AB)
Euklids Methode einen Zirkel zu verwenden funktioniert nicht in der Hilbert Ebene, wir
brauchen deshalb neuen Existenzbeweis (Exercise 10.4)
Proposition (I.13)
(Wenn eine gerade Linie auf einer geraden Linie steht dann entstehen entweder zwei Rechte
Winkel oder zwei Winkel mit der Summe zweier Rechten Winkel)
Kann ersetz werden durch das Resultat von Proposition 9.2 (Kongruenz von Nebenwinkeln)
Proposition (I.14)
(Wenn eine Strecke AB mit einem beliebigem Punkt B gegeben und zwei weitere Strecken
sind so gegeben dass diese nicht auf der gleiche Seite liegen (in Bezug auf AB), und die
Summe der zwei nebeneinanderliegenden Winkel ABC/ABD gleich gross sind wie zwei
Rechte Winkel, dann sind die beiden Linien gerade)
Ist eine Konsequenz von (I.13) (Exercise 10.7)
Proposition (I.15)
(Scheitelwinkel sind kongruent)
Die Kongruenz von Scheitelwinkel ist bereits mit dem Korollar 9.3 abgedeckt.
Proposition (I.16)
(Falls eine Seite eines Dreiecks verlängert ist, dann ist der Aussenwinkel so gross wie die
beiden nicht anliegenden Innenwinkel)
Das Theorem von Aussenwinkeln ist wichtig, deshalb gehen wir den Beweis von Euklid
Schritt für Schritt mit den nötigen Ergänzungen durch.
Proposition 10.3 (Aussenwinkeltheorem (I.16))
In jedem Dreieck ist der Aussenwinkel grösser als jeder der beiden nichtanliegenden
Innenwinkel.
Beweis:
Sei ABC gegebenes Dreieck. Wir wollen nun zeigen dass der Außenwinkel ⦟ACD grösser ist
als der gegenüberliegende Innenwinkel bei A.
Sei hierfür E der Mittelpunkt von AC (I.10), und erweitere BE zu F so dass BE≅EF (Axiom
(C1)).
Zeichne nun die Linie CF, nun sind die Scheitelwinkel bei E gleich (I.15), mit SAS (C6) folgt
dass die Dreiecke ABE und CFE kongruent sind. Somit gilt dass ⦟BAE≅⦟ECF. Um nun den
Beweis zu vervollständigen bleibt zu zeigen dass der Winkel ⦟ECF kleiner ist als der Winkel
⦟ACD.
Hierfür müssen wir wissen, dass die Strecke CF im Innern des Winkels von ⦟ACD liegt. Dies
wiederum können wir mit den Axiomen der Anordnung zeigen.
Da D auf der verlängerten Linie von BC liegt, sind B und D auf der gegenüberliegenden Seite
in Bezug auf die Strecke AC. Gemäss Konstruktion von F haben wir also B und F auf
gegenüberliegenden Seiten (in Bezug auf die Strecke AC). Mit der Proposition 7.1
(Flächenseperation) folgt nun dass D und F auf der gleichen Seite von AC liegen.
Betrachten die Seiten der Strecke BC, da B*E*F gilt, folgt dass E und F auf der gleichen
Seite von BC liegen. Da A*E*C gilt, folgt dass A und E auf der gleichen Seite von AC liegen.
Mit der Transitivität (7.1) folgt dass A und F auf der gleichen Seit sind und somit BC=CD.
Gemäss Definition liegt folglich F im Innern des Winkels ⦟ACD und somit liegt auch die
Strecke CF im Innern.
Es folgt somit gemäss Definition der Ungleichung für Winkel dass der Winkel ⦟BAC kleiner
ist als Winkel ACD.
Proposition (I.17) bis (I.21)
Sind alle ok soweit, ausser dass man bei I.17 die Aussage von Euklid dass zwei Winkel
eines Dreiecks kleiner sind als zwei Rechte Winkel (macht in unserem System keinen Sinn,
da zwei Rechte Winkel nicht einen Winkel darstellen kann) ersetzt durch die Aussage dass
falls α und β zwei Winkel eines Dreiecks sind dann ist α kleiner als der Ergänzungswinkel
von β.
Proposition (I.22)
(Gegeben drei Seitenlängen eines Dreiecks, dann sind zwei Seiten immer länger als die
Dritte)
Ist neben (I.1) unsere zweite Ausnahme, denn ohne zu wissen dass zwei Kreise sich
schneiden können wir die Existenz eines Dreiecks wie es in dieser Proposition gewünscht
wird nicht zeigen. Tatsächlich werden wir später (Excercise 16.11) sehen dass Hilbert
Ebenen existieren in welchen Dreiecken mit drei vordefinierten Strecken nicht existieren.
Proposition (I.23)
(Gegeben Linie mit Punkt A darauf, es wird nun gegebener Winkel konstruiert)
Kann durch Hilberts Axiom (C4) ersetz werden
Proposition (I.24), (I.25), (I.26)=(ASA) und (AAS), (I.27)
Die restlichen Resultate die Euklid ohne Parallel Postulate bewies sind alle so ok
Theorem 10.4
Alle Propositionen von Euklid, (I.1) bis (I.28), mit Ausnahme von (I.1)/(I.22) können in einer
beliebigen Hilbert Ebenen bewiesen werden.
Konstruktionen mit Hilberts Werkzeug
Euklid brauchte unter anderem Massstab und Zirkel für die Beweisführung der Objekte in
seiner Geometrie. Hilbert hingegen benutzen nicht Massstab und Zirkel, sondern er definierte
entsprechende Axiome.
Diese Existenzresultate welche Hilbert als Substitute für Euklids Werkzeuge eingesetzt hat
können wir uns auch als sogenannte Werkzeuge vorstellen:
-Dabei lässt sich (I1) (die Existenz einer Linie durch zwei Punkte) als Masstab
darstellen.
-Das Axiom (C1) kann man sich als Zirkel mit zwei Punkten welche als Transporter für
Linien fungieren vorstellen.
-Das Axiom (C4) als Transporter von Winkeln, welches einen gegebenen Winkel in
einem neuen Punkt reproduzieren kann.
Diese drei Werkzeuge; Zirkel, Teiler und Transporter von Winkeln bezeichnen wir von nun an
als Hilberts Werkzeuge.
Nun können wir das oben vorgestellte Theorem 10.2 nochmals betrachten und die Hilbert
Werkzeuge darauf anwenden. Mit einem Werkzeug pro Schritt bekommen wir folgende
Konstruktion:
Sei Strecke AB gegeben. Nehme C welche nicht auf AB gegeben ist.
1)Zeichne AB
2) Zeichne BC und nehme an dass der Winkel CAB kleiner als CBA ist
3)Transporitere Winkel CAB zu ABE um D zu bekommen
Dann ist ABD das gesuchte Dreieck.
Exercises
Exercise 10.1
Sei ABC gegebener Winkel. Sei die Stecke AB kürzer als die Strecke BC. Nun trage mit dem
„Teiler“ die Strecke AB von B aus auf BC ab und kennzeichne dies mit C’. Nun wissen wir
dass die Strecke AB und BC’ gleich lang sein müssen. Mit dem „Masstab“ verbinden wir nun
die Punkte A und C’. Sei nun D der Mittelpunkt von AC’ (Exercise 10.2).
Wir wissen nun durch Konstruktion dass BA≅BC’ und BD≅BD.
Mit Proposition (I.8) (SSS), folgt dass die Dreiecke DBA und DBC’ kongruent sind
(DBA≅DBC’). Wir haben nun BD im Innern des Dreiecks ABC und wir wissen dass die
Winkel ABD≅CBD. Es folgt somit dass BD den Winkel ABC halbiert.
Exercise 10.2
Sei die Strecke AB gegeben. Wähle ein Punkt C welcher nicht auf der Strecke AB liegt.
Trage mit dem „Transporter“ den Winkel CAB auf die gegenüberliegende Seite von C ab so
dass B als Eckpunkt fungiert und die Strecke BA eine Seite darstellt. Mit dem „Teiler“ tragen
nun die Strecke AC auf die neu konstruierte Seite ab und beschrifte diesen von C
gegenüberliegenden Punkt mit D (es gilt dann AC≅BD). Verbinde C mit D und es folgt dass
die Strecke CD die Strecke AB genau in deren Mittelpunkt schneidet.
Exercise 10.3
Wir wissen dass es auch Punkte gibt die nicht auf l liegen, wir definieren solch einen mit A’.
Mit Exercise 10.4 wissen wir dass dann durch diesen Punkt eine auf l senkrecht stehende
Linie kreieren werden kann. Mit (C4) schliessen wir dann dass es eine eindeutige Strecke
geben muss, die durch Punkt A auf l den selben Winkel kreiert wie jener bei A’ (gemäss
Konstruktion ist dieser ein rechter Winkel). Somit folgt trivialerweise die Behauptung.
Exercise 10.4
Seien B und C zwei Punkte auf l (mit (I2)). Mit Hilfe von (C4) folgt nun dass eine Strecke BX
existiert welche auf der Gegenüberliebenden Seite von l liegt (gegenüber A) und dass der
Winkel XBC≅ABC. Mit C1 existiert ein Punkt A’ auf BX so dass BA≅BA’.
Da A und A’ auf Gegenüberliegenden Seiten, muss AA’ l in einem Punkt Q schneiden der
zwischen A und A’ liegt.
Falls Q=B dann sind die Winkel ABC und A’BC supplementär.
Da diese Winkel kongruent sind, müssen diese rechte Winkel sein, somit steht AA’
rechtwinklig auf l.
Falls Q ungleich B, dann ist BQ≅BQ mit C1 und somit gilt mit SAS dass das Dreieck
ABQ≅A’BQ. Gemäss Definition der Kongruenz von Dreiecken gilt nun dass der Winkel
AQB≅A’QB und somit folgt dass AA’ senkrecht auf l liegt.
Exercise 10.9
Wir wissen dass zwei rechte Winkel kongruent zueinander sind (Proposition 9.6).
Somit folgt die Behauptung mit Proposition (I.4).