Klausur Technische Mechanik III

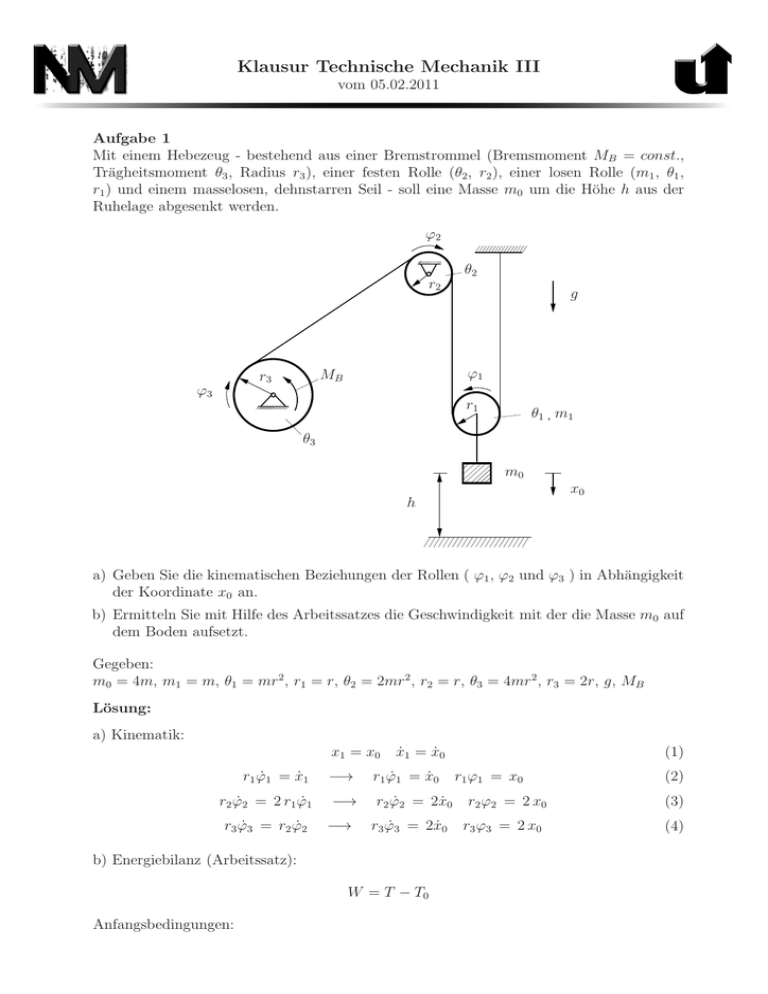
Klausur Technische Mechanik III
vom 05.02.2011
Aufgabe 1
Mit einem Hebezeug - bestehend aus einer Bremstrommel (Bremsmoment MB = const.,
Trägheitsmoment θ3 , Radius r3 ), einer festen Rolle (θ2 , r2 ), einer losen Rolle (m1 , θ1 ,
r1 ) und einem masselosen, dehnstarren Seil - soll eine Masse m0 um die Höhe h aus der
Ruhelage abgesenkt werden.
ϕ2
θ2
r2
ϕ1
MB
r3
g
ϕ3
r1
θ1 , m1
θ3
m0
x0
h
a) Geben Sie die kinematischen Beziehungen der Rollen ( ϕ1 , ϕ2 und ϕ3 ) in Abhängigkeit
der Koordinate x0 an.
b) Ermitteln Sie mit Hilfe des Arbeitssatzes die Geschwindigkeit mit der die Masse m0 auf
dem Boden aufsetzt.
Gegeben:
m0 = 4m, m1 = m, θ1 = mr 2 , r1 = r, θ2 = 2mr 2 , r2 = r, θ3 = 4mr 2 , r3 = 2r, g, MB
Lösung:
a) Kinematik:
x1 = x0
ẋ1 = ẋ0
r1 ϕ̇1 = ẋ1
−→
r1 ϕ̇1 = ẋ0
r2 ϕ̇2 = 2 r1 ϕ̇1
−→
r2 ϕ̇2 = 2ẋ0
r3 ϕ̇3 = r2 ϕ̇2
−→
r3 ϕ̇3 = 2ẋ0
b) Energiebilanz (Arbeitssatz):
W = T − T0
Anfangsbedingungen:
(1)
r1 ϕ1 = x0
r2 ϕ2 = 2 x0
r3 ϕ3 = 2 x0
(2)
(3)
(4)
Klausur Technische Mechanik III
vom 05.02.2011
x0 = x1 = ϕ1 = ϕ2 = ϕ3 = 0
ẋ0 = ẋ1 = ϕ̇1 = ϕ̇2 = ϕ̇3 = 0
T0 = 0
Arbeit:
W = −MB ϕ3 + (m1 x1 + m0 x0 ) g
Kinetische Energie:
T =
1
2
θ3 ϕ̇23 + 12 θ2 ϕ̇22 + 21 θ1 ϕ̇21 + 12 m1 ẋ21 + 21 m0 ẋ20
Die kinematischen Beziehungen werden in die Energiegleichung eingesetzt:
2
1
1
1
1
1
4 2
4 2
ẋ0
2x0
+ (m1 x0 + m0 x0 ) g = θ3
ẋ + θ2
ẋ + θ1
+ m1 ẋ20 + m0 ẋ20
−MB
2 0
2 0
2
r3
2
r3
2
r2
2
r1
2
2
(5)
−MB r23 + (m1 + m0 ) g
2 x0
ẋ20 = 4
θ3 r2 + θ2 r42 + θ1 r12 + m1 + m0
3
2
1
v
(6)
u
u
−MB r23 + (m1 + m0 ) g
√
ẋ0 = t 4
2 x0
θ3 r2 + θ2 r42 + θ1 r12 + m1 + m0
3
Zahlenwerte:
ẋ20
2
1
5 m − MB g1r
2hg
18
m
s
5 m − MB g1r p
2hg
ẋ0 =
18 m
=
(7)
Klausur Technische Mechanik III
vom 05.02.2011
Aufgabe 2
Ein massiver Kreiszylinder rollt schlupffrei auf einer horizontalen Ebene und wird von
einer Feder mit der Federkonstanten c und einem Dämpfer mit der Dämpfungskonstanten
d, die im Abstand a vom Mittelpunkt angreifen, in der dargestellten Mittellage gehalten.
Im abgebildeten Zustand ist die Feder entspannt.
g
ϕ
d
c
a
r
S
m
a) Stellen Sie die Bewegungsgleichung auf.
b) Berechnen Sie den Dämpfungsgrad D, die Eigenfrequenzen ω und ωd des Systems bei
kleinen Auslenkungen.
(Höhenänderungen der Feder und des Dämpfers soll nicht berücksichtigt werden.)
c) Wie groß muss die Dämpfungskonstante d gewählt werden, damit der aperiodische
Grenzfall eintritt.
Gegeben: r, a, m, c, d
Lösung:
a) Freikörperbild:
Klausur Technische Mechanik III
vom 05.02.2011
x
ϕ
Fd Fc
r+a
A
Momentanpol
Bewegungsgleichung (Drallsatz):
θA ϕ̈ = − Fd (r + a) − Fc (r + a)
(8)
Dämpfungskraft und Federkraft:
Kinematik:
Fd = d ẋ
Fc = c x
(9)
x = (r + a) ϕ
ẋ = (r + a) ϕ̇
(10)
eingesetzt in die Bewegungsgleichung:
θA ϕ̈ + d ( r + a )2 ϕ̇ + c ( r + a )2 ϕ = 0
(11)
mit
θA = θS + m r 2 =
folgt:
ϕ̈ +
3
2
1
2
m r2 + m r2 =
d
( r + a )2 ϕ̇ +
2
mr
3
2
3
2
m r2
c
( r + a )2 ϕ = 0
2
mr
(12)
b) die Eigenfrequenz des ungedämpften Systems:
ω02 =
ω0 =
3
2
c
( r + a )2
m r2
r
2c
3m
r +a
r
(13)
(14)
Klausur Technische Mechanik III
vom 05.02.2011
der Dämpfungsgrad:
2 D ω0 =
3
2
d
( r + a )2
2
mr
d
( r + a )2
2
3 ω0 m r
die Eigenfrequenz des gedämpften Systems:
q
√
r +a
2
2
2
2
ωd = ω0 1 − D =
6 m r c − d ( r + a)
3 m r2
D =
c) Der aperiodischer Grenzfall tritt ein wenn D = 1. Die Gleichung (16) folgt:
r
√
r
3 m r2
2c r + a
3 ω0 m r 2
=
=
d =
6mc
( r + a )2
( r + a )2 3 m
r
r+a
(15)
(16)
(17)
(18)