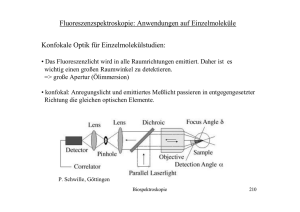
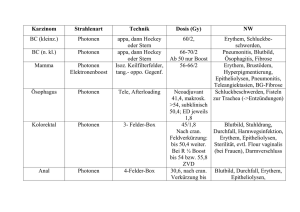
Fluoreszenzintensität ist proportional zur Konzentration angeregter Mo
Werbung

• Fluoreszenzintensität ist proportional zur Konzentration angeregter Moleküle • Zeitliche Änderung der Konzentration angeregter Moleküle: d[S1 ] = dt krad [S1 ] kic [S1 ] kisc [S1 ] ... = 1 [S1 ] ⌧ • Integration ergibt exponentiellen Abfall: [S1 ] = [S1 ]0 e t/⌧ ! I = I0 e t/⌧ Fluoreszenzintensität 1 6 5 4 3 2 0.1 krad 6 5 4 3 kfl 2 0.01 0 2 4 6 8 10 Zeit (ns) • Fluoreszenzquantenausbeute ist definiert als Zahl emittierter Photonen durch Zahl absorbierter Photonen: f = Nem krad [S1 ] krad P = = Nabs [S1 ] k krad + kic + kisc + ... • Bestimmung der Fluoreszenzquantenausbeute: – Vergleich mit Substanz mit bekanntem Ref f – Konzentration so, dass gleiche Absorption 67 – Emissionsspektrum integrieren • Quantenausbeute ist dann: X f 13.2.2 R =R X Iem Ref Iem Ref f Messung von Fluoreszenzabklingzeiten • TCSPC (Time correlated single photon counting) – Anregung mit gepulstem Laser ∗ Detektion einzelner Photonen ∗ Zeitmessung und Histogrammierung der Zeitdifferenzen PulsPhoton ∗ Reversed Start-Stop, damit Uhr nicht so oft gestartet werden muss ∗ Sehr empfindlich ∗ Pile-Up Problem! Zu hohe Emissionsrate: Detektion “falscher” Photonen 13.3 Fluorophore • Bezeichnung für Moleküle, die fluoreszieren können • Oberbegriff für Farbstoffe: Chromophore 68 • Im VIS-Bereich nahezu ausschliesslich konjugierte ⇡-Elektronensysteme Intrinsische • Damit sind solche Fluorophore gemeint, die in biologischen (Makro-) Molekülen vorkommen • Es gibt fluoreszierende Aminosäuren und Nukleinsäuren 69 • • GFP: Green fluorescent protein, aus der Tiefseequalle Aquorea Victoria • Fluorophor geschützt im Innern einer Fass-Struktur 70 Synthetische Fluorophore • Möglichst hohe Fluoreszenzquantenausbeute • je nach Fragestellung: – Gute Löslichkeit – geringe oder hohe Sensitivität auf Umgebung – spezielle Kopplungsgruppen (zur Kopplung an Amino- oder MercaptoGruppen oder Einlagerung in Lipide) • Proteinlabels: Wasserlöslich 71 • FlAsH Labeling • Lipidmarker: Fettsäureketten und polarer (wasserlöslicher) Farbstoff 72 73 13.4 13.4.1 Energieübertragung Resonanzenergietransfer (Förster)- Spektroskopisches Lineal • Theodor Förster: Zwischenmolekulare Energiewanderung und Fluoreszenz (gleiche Farbstoffe) • Stryer, Haugland: Energy transfer: a spectroscopic ruler (unterschiedliche Farbstoffe) • Dipol im Feld eines Dipols: ~D H = µ ~ AE ⇣ ⌘ 3 µ ~ D · ~rˆ ~rˆ µ ~D = µ ~A 3 ⇣r ⌘⇣ ⌘ µ ~ Aµ ~D 3 µ ~ A~rˆ µ ~ D~rˆ = r3 = |~µD | |~µA | /r3 mit = 2 cos ⇥D cos ⇥A sin ⇥D sin ⇥A cos • Transferrate quantenmechanisch: Fermi’s Golden Rule: kT / |h DA⇤ |H| D ⇤ A i| 2 • H ist hierbei die Dipol-Dipol-Wechselwirkung • Nach einiger Rechnung erhält man: 1 1 2 9 ln(10) kt = ⌧0 r6 n4 NA 128⇡ 5 Z d˜ ⌫ fD (˜ ⌫ )✏A (˜ ⌫ )/˜ ⌫4 • ⌧0 ist Fluoreszenzabklingzeit ohne Transfer, also der Kehrwert der Summe aller Raten aus S1 ohne Transfer 74 • Abstandsabhängigkeit: kt / r 6 • Orientierungsabhängigkeit R • Überlappungsintegral d˜ ⌫ fD (˜ ⌫ )✏A (˜ ⌫ )/˜ ⌫4 • Auswahlregeln: Auch spinverbotene Übergänge erlaubt! • Klassische Betrachtung: – Akzeptor_Dipol viel kleiner als Wellenlänge -> kein Unterschied ob Welle oder Wechselfeld – Absorption proportional zu Intensität proportional zum Quadrat des E-Feldes projiziert auf Dipolachse – Absorption proportional zu Wirkungsquerschnitt -> Absorptionsspektrum – E-Feld proportional zu 1/r3 -> Abstandsabhängigkeit – E-Feld proportional zu Emissionswahrscheinlichkeit -> Emissionsspektrum • Mit dem Försterradius r0 s Z 2 9 ln(10) 6 r0 = d˜ ⌫ fD (˜ ⌫ )✏A (˜ ⌫ )/˜ ⌫4 n4 NA 128⇡ 5 • folgt kt = 6 1 r0 ⌧0 r 6 • Abstand Donor-Akzeptor gleich Försterradius: Transferrate gleich inverser Fluoreszenzlebensdauer • Häufiger verwendet: Transfereffizienz Et , das ist das Verhältnis der auf den Akzeptor übertragenen Energiequanten zur Zahl der Anregungen: • Et = kt 1/⌧0 +kt = (r0 /r)6 1+(r0 /r)6 • Transfereffizienz bei r = r0 : Et = 0.5 • Experimentelle Bestimmung der Transferrate: 75 1. Messung der Fluoreszenzintensitäten von Donor (FD ) und Akzeptor (FA ): FA Et = FD + FA 2. Messung der Fluoreszenzintensität des Donors ohne Akzeptor (FD0 ) und mit Akzeptor (FDA ) FDA Et = 1 FD0 3. Messung der Fluoreszenzlebensdauer des Donors ohne Akzeptor (⌧D0 ) und mit Akzeptor (⌧DA ) ⌧DA Et = 1 ⌧D0 • Die Messung über die Fluoreszenzlebensdauern ist besonders robust • Hat man mehrere Spezies vorliegen, haben die Donoren verschiedene Fluoreszenzlebensdauern • Eine Messung mit TCSPC liefert mehrere Komponenten (Summe exponentieller Zerfälle): Identifikation der Spezies möglich • Diese Methode heisst time-resolved FRET (tr-FRET) 13.5 Quenching • Stern-Volmer Gleichung: F0 F 1 = KSV [Q] [Q]? • F0 Fluoreszenzintensität ohne Quenching, F mit Quenching, KSV SternVolmer Konstante • dynamisches Quenching: Bei Annäherung eines sog. Quenchermoleküls kann die Anregungsenergie auf dieses übertragen werden -> Änderung der Fluoreszenz-Quantenausbeute 76 • Zusätzlicher Abregungspfad mit kQ , dadurch Verkürzung der Fluoreszenzabklingzeit • Fluoreszenzquantenausbeute mit Quenching: Q • Es gilt = krad krad + knrad + F0 = F [Q] k [Q]? Q 0 Q • Damit folgt mit ⌧0 = (krad + knrad ) 1 : KSV = kQ ⌧0 • statisches Quenching: Bildung eines nicht fluoreszierenden Komplexes im Grundzustand -> Änderung der Konzentration des leuchtfähigen Farbstoffes • F + Q ⌦ FQ • KSV = K = [FQ] [F][Q] 77 14 14.1 Spinresonanzspektroskopie Spin ~ • Eigenschaft von Fermionen von der Dimension eines Drehimpulses (S), das zu einem messbaren magnetischen Moment führt • Messung nur durch Wechselwirkung mit einem B-Feld möglich, damit ausgezeichnete Richtung • Experimentelle Befunde: ~ zeige in Richtung – Magnetisches Moment in Richtung B-Feld (B z-Achse): µ ~ = SZ = mS ~ mit SZ : z-Komponente des Spins, mS : magnetische Quantenzahl, : gyromagnetisches Verhältnis – mS = ~ – S 2 S, S + 1 . . . S 1, S mit S als der Spinquantenzahl = ~2 S(S + 1) – Für Fermionen (Elektron, Proton, Neutron) S = 1 2 – Für das gyromagnetische Verhältnis gilt: = gµB ~ , wobei das Bohrsche Magneton µB = =g q~ 2m beträgt, womit q 2m – g ist der gyromagnetische Faktor oder auch Landé-Faktor 14.2 Energie im B - Feld • E= ~ = µ ~ ·B ms ~B0 Energieaufspaltung im Magnetfeld: E = ~!L = ~ B0 78 E β α mS=-1/2 mS=1/2 B0 ~ und damit auch µ • Der Vektor S ~ präzediert im magnetischen Feld um ~ den Feldvektor B0 mit der Larmorfrequenz !L = B0 • Einstrahlung von EM Wellen bei der Larmorfrequenz führt zu Resonanzabsorption • Besetzungsstatistik N =e N↵ ~ B0 kT • Bei Einstrahlung ausreichend intensiver Radiowellen: Ausgleich der Besetzungsdifferenz (Sättigung) • Relaxationsmöglichkeiten: – Stösse mit Umgebung (Spin-Gitter-Relaxation, longitudinale Relaxation) – Unterschiedliche Larmorfrequenzen der einzelnen Spins: Spin-Spin oder transversale Relaxation) • Kopplung von Spins: 79