3.3 Halbleiter

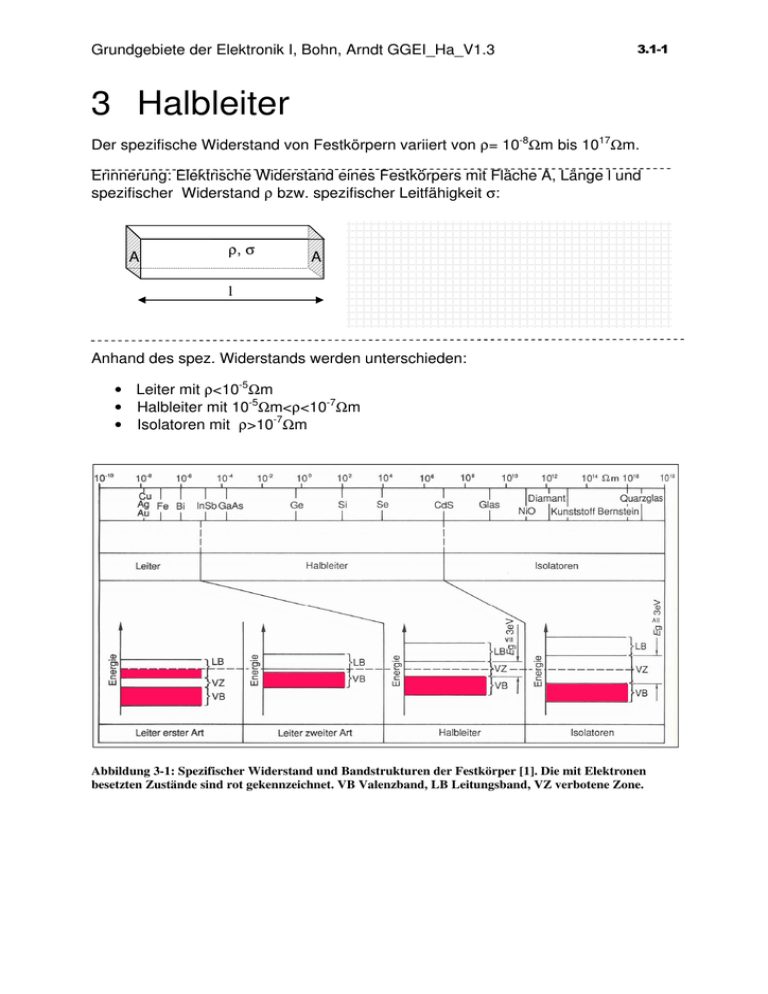
Grundgebiete der Elektronik I, Bohn, Arndt GGEI_Ha_V1.3
3.1-1
3 Halbleiter
Der spezifische Widerstand von Festkörpern variiert von ρ= 10-8Ωm bis 1017Ωm.
Erinnerung: Elektrische Widerstand eines Festkörpers mit Fläche A, Länge l und
spezifischer Widerstand ρ bzw. spezifischer Leitfähigkeit σ:
A
ρ, σ
A
l
Anhand des spez. Widerstands werden unterschieden:
• Leiter mit ρ<10-5Ωm
• Halbleiter mit 10-5Ωm<ρ<10-7Ωm
• Isolatoren mit ρ>10-7Ωm
Abbildung 3-1: Spezifischer Widerstand und Bandstrukturen der Festkörper [1]. Die mit Elektronen
besetzten Zustände sind rot gekennzeichnet. VB Valenzband, LB Leitungsband, VZ verbotene Zone.
Grundgebiete der Elektronik I, Bohn, Arndt GGEI_Ha_V1.3
3.1-2
3.1 Energiebändermodell:
Modell gebundener Elektronen:
• Elektronen, die an isolierte Atome gebunden sind, können sich nur auf
diskreten Energieniveaus aufhalten.
• Die Aufenthaltswahrscheinlichkeit der Elektronen um die Kerne wird durch das
2
Quadrat der Wellenfunktion ψ beschrieben.
• Molekül aus 2 oder 3 Atomen: Durch die Abstoßung der Elektronen ergeben
sich eng benachbarte Energieniveaus. (entspricht Überlagerung der
Wellenfunktionen).
• Festkörper aus N Atomen: Die Energiezustände verschmelzen zu einem
breiten Energieband.
Energiebänder
• Die Energiebänder sind durch verbotene Zonen voneinander getrennt.
• Stromfluß bedeutet, dass Elektronen bei der Bewegung durch den Festkörper
kinetische Energie aufnehmen, also auf eine höhere Energiestufe gehoben
werden.
• Dies ist nur möglich, wenn höhere Energieniveaus frei sind.
• Leiter haben ein teilweise besetzte Energieband und damit frei bewegliche
Elektronen
Abbildung 3-2: Erlaubte Energiezustände im Einzelatom, Molekül und Festkörpern
Valenzband: Oberstes vollständig besetzte Band.
Grundgebiete der Elektronik I, Bohn, Arndt GGEI_Ha_V1.3
3.1-3
Leitungsband: Darüber liegendes teilweise besetztes Band (Leiter) oder leeres
Band (Nichtleiter).
Beispiel Kupferatom (Leiter): 4s-Band halb besetzt (2 Elektronen möglich nach PauliPrinzip):
Abbildung 3-3: Anordnung der Elektronen im Kupferatom
Anmerkung: Beim Einbau eines Kupferatoms in ein Kristall aus reinem Kupfer bleibt
das halb besetzte 4s-Band erhalten. Reines Kupfer ist ein metallischer Leiter.
Bei der Reaktion von Kupfer mit Sauerstoff wird das Elektron in der 4s- Band
gebunden. Das Leitungsband nicht mehr teilweise besetzt. Kuperoxid ist damit ein
Isolator.
Leiter und Isolatoren:
• Leiter: Leitungsband teilweise besetzt
• (Leiter zweiter Art: Leitungsband teilweise besetzt durch Überlappung mit
einem darüber liegenden leeren Band.)
• Halbleiter und Isolatoren: Leitungsband ist leer und vom gefüllten Valenzband
durch verbotene Zone getrennt. Breite = Energiegap E g .
Halbleiter: Eg<= 3eV (ein Elektron muss Spannung von 3V überwinden)
Isolator: Eg> 3eV
Grundgebiete der Elektronik I, Bohn, Arndt GGEI_Ha_V1.3
3.2-4
3.2 Metallische Leiter
Reine Metalle haben wie Kupfer ein teilweise besetztes Leitungsband.
Die Dichte der frei beweglichen Elektronen n ist nahezu unabhängig von der
Temperatur:
Beispiel Kupfer: n = 8,5 ⋅ 10 22 cm 3
Modell der freien Elektronengases:
• Die Leitungselektronen können sich frei gewegen
• Beschreibung der Leitungselektronen als Gas: -> Vernachlässigung
Wechselwirkung mit Atom
Elektrische Leitung:
•
Die Elektronen eines Metalls bewegen sich infolge der Wärmebewegung statistisch in
alle Raumrichtungen.
Wird eine Spannung U angelegt, so ergibt sich ein Elektrisches Feld E=U/d.
•
Kraft durch das elektrische Feld: F=- e ⋅ E -> Beschleunigung a = −
•
Elektronen werden durch Gitterschwingungen, Störungen (Gitterbaufehler,
Verunreinigungen, Korngrenzen) gestreut.
Der Faktor τ beschreibt die mittlere freie Weglänge1: Die Strecke, die ein Elektron bis
zur nächsten Streuung zurücklegt.
•
•
1
•
-> Abbremsung mit Beschleunigung +
•
Mittlere Beschleunigung
vd
τ
dv d
e ⋅ E vd
=−
+
dt
m
τ
Größenordnung hundert Atomabstände
e⋅E
m
(proportional zur Driftgeschwindigkeit vd)
Grundgebiete der Elektronik I, Bohn, Arndt GGEI_Ha_V1.3
•
3.2-5
Abbildung 3-4: Abhängigkeit der Driftgeschwindigkeit von der
Zeit, wenn zum Zeitpunkt t=0 ein elektrisches Feld angelegt
wird.
Bei der stationären Endgeschwindigkeit ist die Beschleunigung gleich Null.
vd ,0 = −
e
⋅ τ ⋅ E 0 = −b ⋅ E 0
m
Die stationäre Geschwindigkeit ist maßgeblich für Stromfluss !!
e
• Beweglichkeit b := ⋅ τ .
m
(3.2-1)
(3.2-2)
Grundgebiete der Elektronik I, Bohn, Arndt GGEI_Ha_V1.3
3.2-6
• Stromdichte:
o Ansatz: Ein infinitesimales Volumen dV = A ⋅ ds bewegt sich mit der
Geschwindigkeit vd0 durch den Leiter:
o Die Ladung dQ im Volumen dV ist das
Produkt aus Volumen dV,
Elektronendichte n=N/V und der
Elektronenladung e.
o Strom ist Ladung pro Zeit
o Stromdichte ist Strom pro Fläche
-> Stromdichte ist das Produkt aus
Geschwindigkeit, Dichte der Ladungsträger
und Elektronenladung
e2
⋅ n ⋅ τ ⋅ E0 = σ ⋅ E0
m
(siehe auch Ohmsches Gesetz: Stromdichte proportional zum elektrischen
Feld)
• Mit (3.2-1) ergibt sich j =
• Leitfähigkeit und Beweglichkeit:
e2
⋅ n ⋅τ
m
o Mit (3.2-2) ergibt sich der Zusammenhang von Leitfähigkeit und
Beweglichkeit:
o Elektrische Leitfähigkeit σ =
σ = e⋅n⋅b
(3.2-3)
o Die elektrische Leitfähigkeit ist das Produkt aus Elektronenladung,
Dichte der freien Ladungsträger und Beweglichkeit.
Grundgebiete der Elektronik I, Bohn, Arndt GGEI_Ha_V1.3
3.2-7
• Temperaturabhängigkeit
o Bei metallischen Leitern liegt die Dichte der freien Elektronen bei
annähernd einem Elektron pro Atom ist annähernd unabhängig
von der Temperatur.
o Die Streuung und damit die Beweglichkeit ist temperaturabhängig:
• Bei sehr tiefen Temperaturen dominiert die
temperaturunabhängige Streuung an Gitterfehlern (dieser Faktor
fällt bei Supraleitung weg!).
• Bei höheren Temperaturen erhöht sich die Streuung durch den
Einfluss von Gitterschwingungen.
-> Der spezifische Widerstand setzt sich zusammen aus dem
temperaturunabhängiger Restwiderstand ρR, und dem Anteil der
Gitterschwingungen ρG(ϑ).
ρ (ϑ ) = ρ R + ρ G (ϑ ) .
(3.2-3)
Abbildung 3-5: Temperaturabhängigkeit des spezifischen Widerstands von Kupfer
Einkristallen unterschiedlicher Reinheit (nach Saeger)
Grundgebiete der Elektronik I, Bohn, Arndt GGEI_Ha_V1.3
3.2-8
o Näherungsformel für die Temperaturabhängigkeit:
• ρ (ϑ ) = ρ (20°C ) ⋅ (1 + α 20 ⋅ ∆ϑ + β 20 ⋅ ∆ϑ 2 + ...)
• Näherung für Temperaturen bis 200°C:
ρ (ϑ ) = ρ (20°C ) ⋅ (1 + α 20 ⋅ ∆ϑ )
Material
Cu
Al
Pt
Konstantan
Kohlenstoff
20
1,78 ·
10−8Ωm
2,64 ·
10−8Ωm
11 ·
10−8Ωm
0,5 ·
10−6Ωm
3,5 ·
10−5Ωm
α20
0,0039 1/K
Einsatz
Kabel, Platinen
0,0039 1/K
Kabel
0,0030 1/K
Temperaturmesswider
stände
Temperaturstabile
Widerstände
Preisgünstige
Widerstände
0,0002 1/K
−0,002 · 1/K
Beispiel: Spezifischer Widerstand von Kupfer bei 100°C:
Grundgebiete der Elektronik I, Bohn, Arndt GGEI_Ha_V1.3
3.3-9
3.3 Halbleiter
Das Leitungsband von Halbleitern ist bei ϑ=0K unbesetzt.
Grund: Die Elektronen der äussersten Schale werden alle für die chemische Bindung
verwendet. Damit ist das Valenzband voll, das Leitungsband leer.
Elementhalbleiter aus der IV. Gruppe des Periodensystems kristallisieren in einer
tetraedrischen Diamantstruktur. Jedes Atom hat vier Nachbarn. Weitere Halbleiter mit
tetraedrischen Gittern ergeben sich nach untenstehender Tabelle:
Abbildung 3-6: Arten von Halbleitern
Mischkristalle auf Basis von III-V-Halbleitern ermöglichen die Einstellung der Breite
der verbotenen Zone.
Wichtgste Materialien: Silizium (Si) z. B. für Mikroprochips, Gallium-Arsenid (GaAs)
für Optoelektronik.
Leitung in Halbleitern erfolgt entweder durch Eigenleitung oder durch
Störstellenleitung:
Grundgebiete der Elektronik I, Bohn, Arndt GGEI_Ha_V1.3
3.3.1
3.3-10
Eigenleitung
Alle Valenzelektronen werden für
die chemische Bindung zu den 4
Nachbaratomen eingesetzt.
• Bei T=0 (absoluter Nullpunkt der
Temperatur) ist keine elektrische
Leitung möglich.
Hier ist das Valenzband voll, das
Leitungsband leer.
•
•
•
•
Durch Energiezufuhr
(Temperaturerhöhung, Lichteinfall)
werden Elektronen aus dem
Valenzband VB gelöst und über
den Energiegap Eg ins
Leitungsband LB angehoben. Es
entsteht ein freies Elektron und ein
freies Loch.
Stromfluss erfolgt durch Elektronen
im Leitungsband und Löcher
(fehlende Elektronen) im
Valenzband.
Da freie Elektronen und Löcher
nur paarweise erzeugt werden ist
die Dichte der (freien) Elektronen
n gleich der Dichte der (freien)
Löcher p.
n= p
Abbildung 3-7: Eigenleitung
(3.3-1)
•
Wird an das Kristall Spannung angelegt, dann fließen die Elektronen (-) zur
Anode (+) und die Löcher (+) zur Kathode (-) .
•
•
Der Gesamtstrom ist die Summe aus Elektronenstrom und Löcherstrom.
Die Elektrische Leitfähigkeit setzt sich aus dem Beiträgen der Elektronen und
Löcher zusammen:
σ = e ⋅ (n ⋅ µ n + p ⋅ µ p )
(3.3-2)
Grundgebiete der Elektronik I, Bohn, Arndt GGEI_Ha_V1.3
3.3-11
Abbildung 3-8: Eigenschaften unterschiedlicher Halbleitertypen bei ϑ=300K.
Beweglichkeit:
•
•
Elektronen haben eine höhere Beweglichkeit als Löcher
Die Beweglichkeit sinkt bei Temperaturerhöhung leicht:
µ (T ) = µ 300 K ⋅ (ϑ / 300 K ) −3 / 2
(3.3-3)
Dichte der freien Elektronen und Löcher = intrinsische Trägerdichte ni:
•
Da immer ein freies Elektron und freies Loch zusammen generiert werden ist
ni = n = p
.
•
Die Trägerdichte wird mit Hilfe der Fermi-Dirac-Statistic berechnet:
•
•
ni (ϑ ) = n = p = N L ⋅ NV ⋅ e
−
− Eg
2⋅k ⋅ϑ
3
2
= ni 0 ⋅ ϑ ⋅ e
− Eg
2⋅k ⋅ϑ
(3.3-4)
wobei NL effektive Zustandsdichte im Leitungsband, NV effektive
Zustandsdichte im Valenzband, Eg Bandgap in eV, k Stefan-BoltzmannKonstante, ϑ absolute Temperatur in K, ni0 Konstante für
Ladungsträgerdichte:
Leitungsfähigkeit:
•
Leitung findet statt basierend auf Elektronen und Löchern:
•
Die Gleichung 3.2-3 kann erweitert werden zu:
σ = e ⋅ n ⋅ µn + e ⋅ p ⋅ µ p
(3.3-5)
Grundgebiete der Elektronik I, Bohn, Arndt GGEI_Ha_V1.3
3.4-12
3.4 Störstellenleitung
Der Einbau von Fremdatomen (=Störstellen) ins Kristallgitter des Halbleiters führt zu
erheblicher Veränderung des Widerstands.
3.4.1
n-Halbleiter basierend auf Silizium:
Silizium wird mit Atomen der V. Gruppe dotiert (Bsp. Phosphor).
Jedes Störatom bringt ein Elektron ein, das keine
Bindung zum Nachbaratom eingeht.
„Donator“ (lateinisch donare = geben)
• Das Elektron kann durch Zugabe der geringe
Ionisierungsenergie ED vom Atom abgetrennt werden.
Es dient dann als freies Elektron als Ladungsträger
im Leitungsband.
Die Fermi- Energie2 EF liegt knapp (Abstand ED/2)
unter der Bandkante des Leitungsbandes EL
(Beginn des Leitungsbandes ).
•
•
•
Die Ionisierungsenergie ED ist gering (mV).
Abbildung 3-9: Ionisierungsenergie ED bei Silizium.
•
2
Verhalten bei 300K (Raumtemperatur):
o Aufgrund der niedrigen Ionisierungsenergie sind alle Störatome
ionisiert. Alle eingebrachten Elektronen dienen zur Leitung.
o Leitung beruht auf negativen, freien Elektronen. Diese sind gegenüber
den positiven Löchern in der Mehrheit („Majoritätsladungsträger“)
n-leitender Halbleiter oder n-Typ
o Die Löcher sind gegenüber den freien Elektronen in der Minderheit
(„Minoritätsladungsträger“).
Fermi- Energie: Elektrochemisches Potential bzw. mittleres Energieniveau der
Elektronen im Kristall. Wenn die Elektronen durch geringe Energiezugabe ins
Leitungsband wechseln können liegt die Fermi- Energie somit nur knapp unter dem
Energie-Niveau (Bandkante) des Leitungsbandes EL.
Grundgebiete der Elektronik I, Bohn, Arndt GGEI_Ha_V1.3
3.4-13
Grundgebiete der Elektronik I, Bohn, Arndt GGEI_Ha_V1.3
3.4.2
3.4-14
p-Halbleiter basierend auf Silizium:
Dotierung mit Element aus der III. Gruppe
Jedes Störatom bringt ein fehlendes Elektron ein.
-> Akzeptor (lateinisch akzeptare = nehmen)
Durch geringe Energiezufuhr kann das fehlende
Elektron von einem Elektron des Nachbaratoms
aufgefüllt werden. Es dient als freies Loch im
Valenzband zum Ladungstransport.
Die Fermi- Energie EF liegt knapp (Abstand ED/2)
über der Bandkante des Valenzbandes EV.
• Die Ionisierungsenergien ED sind gering (mV).
• Verhalten bei 300K (Raumtemperatur):
o Aufgrund der niedrigen Ionisierungsenergie sind alle Störatome
ionisiert. Alle eingebrachten Löcher dienen zur Leitung.
o Leitung beruht auf positiven Löchern (Majoritätsladungsträger)
p- leitender Halbleiter oder p-Typ
o Die freien Elektronen sind in diesem Fall in der Minderheit gegenüber
den Löchern („Minoritätsladungsträger“).
•
•
•
•
Maß der Dotierung:
Das Maß der Dotierung wird so gewählt, dass bei der Betriebstemperatur die
Konzentration der Donatoren nD oder Akzeptoren nA deutlich höher ist als die
intrinsische Ladungsträgerdichte.
n D >> ni und n A >> ni
Dadurch entsteht ein p oder n-dotierter Halbleiterbereich.
Grundgebiete der Elektronik I, Bohn, Arndt GGEI_Ha_V1.3
3.4.3
3.4-15
Verhalten in Abhängigkeit von der Temperatur:
I) Bereich der Störstellenreserve:
• Bei 0K sind noch keine
Fremdatome ionisiert.
• Bei höheren Temperaturen
werden die Fremdatome
ionisiert.
Nach der Fermi- Dirac- Statistik
ergibt sich die Konzentration der
freien Elektronen bei nHalbleiter
E
n(ϑ ) =
nD ⋅ N L − 2⋅kD⋅ϑ
⋅e
2
wobei ED Ionisierungsenergie
der Donatoratome, nD
Konzentration der Donatoratome
und NL effektive Zustandsdichte
im Leitungsband.
•
Abbildung 3-10: Ladungsträgerdichte bei nTyp-Silizium in Abhängigkeit von der
Temperatur. Dotierung: Phosphor, nD=1015 /cm3
Die Konzentration der freien Löcher bei p-Halbleitern ist:
E
p (ϑ ) =
n A ⋅ NV − 2⋅kA⋅ϑ
⋅e
2
wobei EA Ionisierungsenergie der Akzeptoratome, nA Konzentration der
Akzeptoratome und NV effektive Zustandsdichte im Valenzband.
II) Bereich der Störstellenerschöpfung
• Alle Störstellen sind ionisiert.
• Weitere Temperaturerhöhung führt nur noch zu einer Steigerung der
intrinsischen Ladungsträgerdichte ni.
• Bei n-Dotierung ist die Ladungsträgerdichte der Majoritätsladungsträger:
2
n
n 
n = D +  D  + ni2
2
 2 
(3.4-1)
wobei nD Konzentration der Donatoratome, ni intrinsische
Ladungsträgerdichte.
•
Das Produkt der Dichte der freien Elektronen und Löcher ist bei
gegebener Temperatur eine Konstante unabhängig von der Dotierung:
n ⋅ p = ni2
(3.4-2)
Grund: Ein freies Elektron ist ein überflüssiges Elektron. Ein freies Loch ist ein
fehlendes Elektron für die Bindung der Atome im Kristall. Trifft das freie
Grundgebiete der Elektronik I, Bohn, Arndt GGEI_Ha_V1.3
3.4-16
Elektron auf das Loch eliminieren sich beide. Eine hohe Konzentration von
freien Elektronen führt damit zu einer niedrigen Konzentration von Löchern
und umgekehrt.
•
•
Bei n-Dotierung ergibt sich die Ladungsträgerdichte p der
Minoritätsladungsträger nach (3.4-2):
n2
p= i
n
Bei p-Dotierung gilt entsprechend für die Ladungsträgerdichte der
Majoritätsladungsträger:
2
n
n 
p = A +  A  + ni2
2
 2 
(3.4-3)
und für die Minoritätsladungsträger
n=
ni2
.
p
wobei nA Konzentration der Akzeptoratome, ni intrinsische
Ladungsträgerdichte.
III) Überhöhte Temperatur
• Bei überhöhter Temperatur übersteigt die intrinsische Ladungsträgerdichte die
Dichte der Ladungsträger durch Dotierung.
• Leitung erfolgt hauptsächlich aufgrund der intrinsischen Ladungsträgerdichte.
Eigenleitung.
• Die Dotierung wird unwirksam. Die Folge ist ein Funktionsausfall der durch
Dotierung erzeugten Bauelemente wie Dioden, Transistoren, ... .
Temperaturbereich3 für elektronische Schaltungen:
• Bereich, in dem die Dotierung in den p- und n- dotierten Zonen wirksam ist .
• Beispiel -40°C bis 175°C (auf dem Chip).
• Der Temperaturbereich liegt im Bereich der Störstellenerschöpfung.
3
Beispiel: Eine Elektronische Schaltung z. B. Zählerbaustein mit Dioden wird erhitzt, Strom und
Temperatur gemessen. Ab 100°C Stromerhöhung, über 175°C Funktionsausfall.
Grundgebiete der Elektronik I, Bohn, Arndt GGEI_Ha_V1.3
3.5-17
3.5 pn- Übergang
Beispiel:
Abrupter pn-Übergang dotiert mit
n A = 1 ⋅ 1016 / cm 3
n D = 2 ⋅ 1016 / cm 3
a) p- und n-leitendes Silizium in Kontakt
b) Störstellenkonzentration
c) Dichteverlauf der beweglichen Ladungsträger
• Weit weg vom Übergang sind die
Majoritätsdichten identisch mit den
Störstellenkonzentrationen
• Die Minoritätsdichten ergeben sich nach
(9-31)
• Infolge des Konzentrationsgefälles
diffundieren Elektronen ins p-Gebiet und
Löcher ins n-Gebiet. Die Übergangszone
verarmt. Die minimale
Ladungsträgerkonzentration ist hier
(n+p)=2ni
d) Raumladungsgebiete
• Alle Akzeptoren am Rand des p-Gebiets
haben je ein Elektron aufgenommen ->
negative Raumladungszone. Alle Donatoren
am Rand des n-Gebiets haben je ein Elektron
abgegeben-> positive Raumladungszone.
• In beiden Zonen sind gleich viele Ladungen,
deshalb gilt
d n ⋅ nD = d p ⋅ n A
(3.5-1)
(Eigentlich Vn ⋅ n D
= Vp ⋅ nA )
e) Potentialverlauf
• Äquivalent zu den geladenen Platten eines
Kondensators ergibt sich ein Potentialgefälle
Die Potentialdifferenz ist die Spannung Ud.
Diese Spannung entsteht aufgrund der
Diffusion der Ladungsträger ->
Diffusionsspannung.
• Berechung über Boltzmann-Näherung der
Fermi-Dirac-Verteilung:
Ud =
k ⋅ ϑ n A ⋅ nD
ln
e
ni2
(3.5-2)
Temperaturspannung
k ⋅ϑ
=: U T
(3.5-3)
e
U T = 25,9mV bei Raumtemperatur (300K)
Faktor
Die Raumladungszonen erzeugen ähnlich wie beim Kondensator ein elektrisches Feld.
Die Breite der Raumladungszonen ergibt sich aus der Analyse des Potentialverlaufs
d = dn + d p =
2ε r ⋅ ε 0 ⋅ U d n A + n D
⋅
e
n A ⋅ nD
(3.5-4)
Grundgebiete der Elektronik I, Bohn, Arndt GGEI_Ha_V1.3
3.5-18
Prinzip des pn-Übergangs
a) Keine Spannung
P-Dotierung
N-Dotierung
B
Si
B
Si
B
Si
P
Si
P
Si
Si
B
Si
B
Si
P
Si
P
Si
P
B
Si
B
Si
B
Si
P
Si
P
Si
Si
B
Si
B
Si
P
Si
P
Si
P
Grundgebiete der Elektronik I, Bohn, Arndt GGEI_Ha_V1.3
3.5-19
b) Spannung in Flußrichtung
P-Dotierung
N-Dotierung
B
Si
B
Si
B
Si
P
Si
P
Si
Si
B
Si
B
Si
P
Si
P
Si
P
B
Si
B
Si
B
Si
P
Si
P
Si
Si
B
Si
B
Si
P
Si
P
Si
P
c) Spannung in Sperrrichtung
P-Dotierung
N-Dotierung
B
Si
B
Si
B
Si
P
Si
P
Si
Si
B
Si
B
Si
P
Si
P
Si
P
B
Si
B
Si
B
Si
P
Si
P
Si
Si
B
Si
B
Si
P
Si
P
Si
P
Grundgebiete der Elektronik I, Bohn, Arndt GGEI_Ha_V1.3
3.5-20
zu b) Spannung in Flussrichtung
+ an p, - an n-Gebiet
• Die angelegte Spannung baut die Diffusionsspannung ab.
• Die Bandkantenverschiebung wird reduziert auf
e ⋅ (U d − U )
•
•
•
Die Breite der zu überwinden Raumladungszone (=Verarmungszone) wird
reduziert wenn Ud durch Ud-U ersetzt wird. (siehe 3.5-4)
Bewegliche Ladungsträger (z. B. Elektronen aus n-Gebiet) reichern sich in der
Verarmungszone an, dringen ins benachbarte Gebiet (p-Gebiet) ein und
rekombinieren dort mit Majoritäten (Löchern).
Stromfluß
 ne⋅k⋅U⋅ϑ

− 1
I = I S ⋅  e
(3.5-5)


wobei IS Sperrsättigungsstrom4, Größenordnung 1nA für Si, 1µA für Ge,
U angelegte Spannung, ϑ absolute Temperatur in K, n Faktor 1,0 bis 2.
Vereinfacht: I ~ e
U
kϑ
stark von Spannung und Temperatur abhängig.
zu c) Spannung in Sperrrichtung
+ an p, - an n-Gebiet
• Die angelegte Spannung erhöht die Diffusionsspannung.
• Die Bandkantenverschiebung wird erhöht auf
e ⋅ (U d + U )
•
Die Breite der zu überwinden Raumladungszone (=Verarmungszone) wird
erhöht wenn Ud durch Ud+U ersetzt wird. (siehe 3.5-4)
kein Stromfluß
Kennlinie einer Diode: Flussrichtung und Sperrrichtung
Abbildung 3-11: Diodenkennlinie von Silizium und Germanium
4
Sperrstrom bei großer angelegter Sperrspannung, allerdings nicht Fall des Durchbruchs !!
Dieser Wert ist von der Größe der Diode abhängig. Bsp.:
Grundgebiete der Elektronik I, Bohn, Arndt GGEI_Ha_V1.3
3.5-21
Symbol: Pfeil zeigt die Stromrichtung im Durchlassrichtung
IF an:
3.5.1
•
Bauarten von Dioden:
Photodioden auf Chip für Kamera: Größe5x5µm, Strom mehrere µA
Abbildung 3-12: Photodiodenarray, Firma Melexis
•
Diode in Schaltung: Größe 2mm x 5mm Strom bis 20mA , Preis
5Ct (1N4001)
Abbildung 13: Weitere Bauformen von Dioden
•
Leuchtdioden: Lichtemission bei der Rekombination der Ladungsträger
•
Leistungsdioden für elektrische Maschinen: Größe 100mm (Durchmesser),
Strom bis 10000A, Preis >>100€
Abbildung 3-14: DNB 64, Strom im Dauerbetrieb 3400A, Spannung 3600V,
http://www.dynexsemi.com
Grundgebiete der Elektronik I, Bohn, Arndt GGEI_Ha_V1.3
3.5.2
3.5-22
Anwendungsbeispiele:
1. Temperatursensor: Beispiel Überwachung der Chiptemperatur in Ihrem
Laptop!!
2. Einweggleichrichter: Die Diode lässt einen hohen Strom in Durchlassrichtung
fließen (mA bis A) In Sperrrichtung fließt nur ein geringer Strom (nA bis µA).
Deshalb wird sie zur Gleichrichtung von Wechselstrom (geliefert von
Transformator) eingesetzt.
Beispiel: Gleichrichtung einer Wechselspannung von 10V Amplitude, 50Hz
Frequenz
Vorteil: geringer Aufwand
Nachteil: hohe Welligkeit der Ausgangsspannung, da der Kondensator während
circa
entladen wird.
Grundgebiete der Elektronik I, Bohn, Arndt GGEI_Ha_V1.3
3.5-23
3. Brücke
Brückengleichrichter:
gleichrichter: Die Positive und die negative Halbwelle werden in
Gleichspannung umgesetzt
Beispiel: Gleichrichtung einer Wechselspannung von 10V Amplitude, 50Hz
Frequenz
Vorteil: Geringe Welligkeit der Ausgangsspannung, da der Kondensator nur
während circa
entladen wird.
Grundgebiete der Elektronik I, Bohn, Arndt GGEI_Ha_V1.3
3.5-24
Zenerdiode:
•
•
•
•
•
•
•
Prinzip: Erhöhung des Sperrstroms bei hoher Sperrspannung:
Zenereffekt: Durch die große
Feldstärke in der
Verarmungszone werden
Elektronen aus dem Valenzband
des p-Materials über die
Verarmungszone ins
Leitungsband des n-Material
des n-Materials gezogen
(tunneln).
Lawinenmultiplikation:
Elektronen werden durch die
hohe Feldstärke so
beschleunigt, dass sie beim
Zusammenprall mit dem Gitter
ein Elektronen-Loch-Paar
Abbildung 3-15: a) Zener-Effekt, b)
erzeugen. Diese Ladungsträger
Lawinenmultiplikation
werden ebenfalls beschleunigt
und erzeugen neue ElektronenLoch-Paare...
Beide Effekte haben
gegenläufige
Temperaturabhängigkeit
-> bei 5,6V beste
Temperaturkonstanz
Der Strom durch eine Zenerdiode erhöht sich oberhalb der
Zenerspannung stark.
Deshalb wird eine Zenerdiode zur Spannungsstabilisierung eingesetzt.
Abbildung 3-16: Strom- Spannungskennlinie unterschiedlicher Zenerdiodentypen. Beispiel ZPD 6.8:
Oberhalb von 6,8V erhöht sich der Zenerstrom stark.
Grundgebiete der Elektronik I, Bohn, Arndt GGEI_Ha_V1.3
Anwendung: Spannungsstabilisierung
3.5-25
Grundgebiete der Elektronik I, Bohn, Arndt GGEI_Ha_V1.3
3.6 Transistoren
3.6.1
Bipolartransistor
Prinzip:
• Beispiel Emitterschaltung
Emitterschaltung
• Spannung UEB<1V an EmitterEmitter
Basis in Durchlassrichtung
Basis
• Spannung an Kollektor-Basis
Kollektor Basis in
Sperrrichtung (z. B. 10V)
• Elektronen fließen vom Emitter
zur Basis
• Dort teilt sich Strom auf in
geringen Basisstrom IB und sehr
hohen Kollektorstrom IC. Grund:
Die Basis ist so dünn, dass der
Kollektorstrom beinahe so groß
Kollektorstrom
ist wie der Emitterstrom.
• Stromverstärkungsfaktor
I
• B = C = 50..200 je nach Typ
Ib
•
Abbildung 3-17
17:: Prinzip des Transistors,
Emitterschaltung
Schichtaufbau:
Abbildung 3--18:: Aufbau eines npn-Transistors
npn Transistors
n+5 stark n-dotiert,
dotiert, nn schwach n-dotiert
n dotiert
Quelle Wikipedia.
Quelle
Wikipedia
5
Eine starke Dotierung n+ sorgt für einen großen Leitwert und damit für einen geringe
Spannungsverlust.
3.6-26
Grundgebiete der Elektronik I, Bohn, Arndt GGEI_Ha_V1.3
3.6-27
Herstellung:
Abbildung 3-19: Herstellungsvorgang für zwei nebeneinander liegende Transistoren in Planartechnik
Grundgebiete der Elektronik I, Bohn, Arndt GGEI_Ha_V1.3
Hauptmerkmale:
3.6-28
Grundgebiete der Elektronik I, Bohn, Arndt GGEI_Ha_V1.3
Kennlinien von Bipolar-Transistoren: Zusammenhänge von IB, UBE, IC und UCE
Praxisbeispiel:
Auszug aus dem Datenblatt des Leistungstransistors BD2N3055:
Bei einem Basisstrom von 200mA und einem Kollektorstrom von 4A liegt die
Kollektor-Emitterspannung bei
3.6-29
Grundgebiete der Elektronik I, Bohn, Arndt GGEI_Ha_V1.3
3.6-30
Transistor als Verstärker:
1. Grundschaltungen
Hoch- und
Niederfrequenzverstärker
Schalter
Impedanzwandler
Hochfrequenzverstärker
Grundgebiete der Elektronik I, Bohn, Arndt GGEI_Ha_V1.3
3.6-31
Grundgebiete der Elektronik I, Bohn, Arndt GGEI_Ha_V1.3
3.6-32
Feldeffekt-Transistor
•
Die Steuerspannung beeinflusst die Leitfähigkeit einer dünnen
Oberflächenschicht im Halbleiterkristall
•
Beispiel: MOS-FET6 p-Kanal Anreicherungstyp:
Abbildung 3-20: Prinzip des CMOS-Transistors
•
•
•
6
An der Senke (Drain) liegt die negative Spannung UDS an.
Ohne Steuerspannung UGS fließt kein Strom zwischen Quelle (Source) und
Senke da sich eine Diode in Sperrbetrieb zwischen dem n-Silizium und der
p-Senke ergibt.
Eine negative Steuerspannung UGS am Gate verdrängt die Elektronen ins
Kristallinnere und zieht Löcher aus dem Kristall an. Der Kanal wird mit
Ladungsträgern angereichert (-> „Anreicherungstyp“), so dass
oberflächennahe p- leitende Schicht („p-Kanal“) entsteht.
Metall Oxid Silizium: Das Gate ist durch eine isolierende Metalloxid-Schicht isoliert. Damit kann
unabhängig von der Gate- Spannung kein Gate- Strom fließen.
Grundgebiete der Elektronik I, Bohn, Arndt GGEI_Ha_V1.3
Arten von CMOS-Transistoren:
3.6-33
Grundgebiete der Elektronik I, Bohn, Arndt GGEI_Ha_V1.3
3
3.6-34
Halbleiter ....................................................................................................... 3.1-1
3.1
Energiebändermodell: ............................................................................ 3.1-2
3.2
Metallische Leiter ................................................................................... 3.2-4
3.3
Halbleiter ................................................................................................ 3.3-9
3.3.1
3.4
Eigenleitung .................................................................................. 3.3-10
Störstellenleitung .................................................................................. 3.4-12
3.4.1
n-Halbleiter basierend auf Silizium: ............................................... 3.4-12
3.4.2
p-Halbleiter basierend auf Silizium: ............................................... 3.4-14
3.4.3
Verhalten in Abhängigkeit von der Temperatur: ............................ 3.4-15
3.5
pn- Übergang ....................................................................................... 3.5-17
3.5.1
Bauarten von Dioden: ................................................................... 3.5-21
3.5.2
Anwendungsbeispiele: .................................................................. 3.5-22
3.6
Transistoren ......................................................................................... 3.6-26
3.6.1
Bipolartransistor ............................................................................ 3.6-26