1 Grundkonzepte von Datenbanken

Vorlesung Datenbanken
1
Wintersemester 2013/14
Grundkonzepte von Datenbanken
1.1 Datenbanken und ihre Benutzer
Eine Datenbank ist eine Sammlung von zusammengehörigen Daten.
Sie repräsentiert einen Ausschnitt der realen Welt, eine sogenannte
“Mini–Welt” (Universe of Discourse), und deren Veränderungen.
Beispiel (U NIVERSITY Datenbank)
Der Studentenkartei einer Universität enthält Datensätze zu Studierenden,
welche nach unterschiedlichen Gesichtspunkten (z.B. Name oder
Geburtsdatum) geordnet sind.
Die Datenbankbenutzer können die Daten durchsuchen (search), Daten
recherchieren (retrieve) und verändern (update).
Prof. Dr. Dietmar Seipel
1
Vorlesung Datenbanken
Wintersemester 2013/14
Ein Datenbank–Management–System (DBMS) ist ein universelles
Softwarepaket zur Definition, Konstruktion und Manipulation von
Datenbanken für unterschiedliche Anwendungen.
• Definition einer Datenbank: Spezifikation der Datentypen, der
Datenstrukturen und der Bedingungen (Constraints) an die Daten.
• Konstruktion einer Datenbank: Speicherung der Daten auf einem vom
DBMS kontrollierten Speichermedium.
• Manipulation einer Datenbank: Anfragen an die Datenbank um spezielle
Daten zu erhalten, Veränderung der Daten bei Änderungen in der
Mini–Welt, Generierung von Reports über die Daten.
Die Datenbank und das DBMS formen ein Datenbanksystem.
Prof. Dr. Dietmar Seipel
2
Vorlesung Datenbanken
Wintersemester 2013/14
Users / Programmers
DATABASE
SYSTEM
?
Application Programs / Queries
DBMS
SOFTWARE
?
Software to Process
Queries / Programs
?
Software to Access
Stored Data
7
/
I
R
Stored Database
Definition
(Meta-Data)
Stored
Database
A simplified database system environment.
Prof. Dr. Dietmar Seipel
3
Vorlesung Datenbanken
Wintersemester 2013/14
1.1.1 Beispiel: die U NIVERSITY–Datenbank
Die Datenbank besteht aus 5 Tabellen (Relationen), welche jeweils
Datensätze (Zeilen, Tupel) desselben Typs enthalten.
Die Relation S TUDENT speichert zu jedem Studierenden den Namen, die
Matrikelnummer, das Fachsemester und das Hauptfach.
S TUDENT
Prof. Dr. Dietmar Seipel
Name
StudentNumber
Class
Major
Smith
17
1
COSC
Brown
8
2
COSC
4
Vorlesung Datenbanken
Wintersemester 2013/14
Zu jedem Kurs werden Name, Nummer (im Vorlesungsverzeichnis),
Kreditpunkte und das verantwortliche Department in C OURSE gespeichert.
C OURSE
CourseName
Prof. Dr. Dietmar Seipel
CourseNumber
CreditHours
Department
Intro to Computer Science
COSC1310
4
COSC
Data Structures
COSC3320
4
COSC
Discrete Mathematics
MATH2410
3
MATH
Databases
COSC3380
3
COSC
5
Vorlesung Datenbanken
Wintersemester 2013/14
Da ein Kurs in verschiedenen Semestern von unterschiedlichen Dozenten
gehalten werden kann, wird für jedes Semester ein entsprechender
Datensatz – mit einem eindeutigen Identifikator – in S ECTION gespeichert.
S ECTION
Prof. Dr. Dietmar Seipel
SectionIdentifier
CourseNumber
Semester
Year
Instructor
85
MATH2410
Fall
2005
King
92
COSC1310
Fall
2005
Anderson
102
COSC3320
Spring
2006
Knuth
112
MATH2410
Fall
2006
Chang
119
COSC1310
Fall
2006
Anderson
135
COSC3380
Fall
2006
Stone
6
Vorlesung Datenbanken
Wintersemester 2013/14
Für jeden Studierenden werden seine besuchten Veranstaltungen mit Noten
gespeichert. Dabei werden zur Bezeichnung der Studierenden und
Veranstaltungen Identifikatoren verwendet, die sich auf die entsprechenden
Relationen S TUDENT und S ECTION beziehen.
G RADE _R EPORT
Prof. Dr. Dietmar Seipel
StudentNumber
SectionIdentifier
Grade
17
112
B
17
119
C
8
85
A
8
92
A
8
102
B
8
135
A
7
Vorlesung Datenbanken
Wintersemester 2013/14
Die Relation P REREQUISITE enthält die Voraussetzungen der Kurse.
P REREQUISITE
CourseNumber
PrerequisiteNumber
COSC3380
COSC3320
COSC3380
MATH2410
COSC3320
COSC1310
Für jeden Kurs gibt es so viele Tupel wie er Voraussetzungen hat.
Prof. Dr. Dietmar Seipel
8
Vorlesung Datenbanken
Wintersemester 2013/14
Anfragen:
• Gib eine Aufstellung, d.h. eine Liste der Kurse und Noten (Grades),
von Smith aus
• Liste die Namen von Studenten und Noten, welche den
Datenbanken–Kurs im Herbst 2006 besucht haben, auf
• Was sind die Voraussetzungen für den Datenbanken–Kurs?
Updates:
• Ändere die Klasse von Smith auf 2
• Gib die Note A ein für den Studenten Smith im Datenbanken–Kurs
des letzten Semesters
Prof. Dr. Dietmar Seipel
9
Vorlesung Datenbanken
Wintersemester 2013/14
Aus den vorliegenden Relationen kann man Reports (Sichten) generieren:
T RANSCRIPT
StudentTranscript
StudentName
Smith
Brown
Prof. Dr. Dietmar Seipel
CourseNumber
Grade
Semester
Year
SectionId
COSC1310
C
Fall
2006
119
MATH2410
B
Fall
2006
112
MATH2410
A
Fall
2005
85
COSC1310
A
Fall
2005
92
COSC3320
B
Spring
2006
102
COSC3380
A
Fall
2006
135
10
Vorlesung Datenbanken
Wintersemester 2013/14
Dabei können z.B. die besuchten Veranstaltungen mit Noten nach
Studierenden gruppiert werden (siehe oben),
oder es können die Voraussetzungen der Kurse nach Kursen gruppiert
werden (siehe unten).
P REREQUISITES
CourseName
CourseNumber
Databases
COSC3380
Data Structures
COSC3320
Prof. Dr. Dietmar Seipel
PrereqName
PrereqNumber
Data Structures
COSC3320
Discrete Math.
MATH2410
Intro to CS
COSC1310
11
Vorlesung Datenbanken
Wintersemester 2013/14
1.1.2 Charakteristika des Datenbankansatzes
Datenintegration und Datenkonsistenz
Integration und konsistente Verwaltung der Daten der unterschiedlichen
Benutzergruppen; kontrollierte Redundanz, da sonst
Speicherplatzverschwendung und unnötiger Aufwand bei der Wartung
des Datenbestandes und eventuelle Inkonsistenzen in den Daten.
Systemkatalog (Data Dictionary)
enthält Meta–Daten: Informationen zur Datenstruktur, den Typen und
Speicherformaten der einzelnen Datenelemente, sowie
Integritätsbedingungen an die Daten (selbstbeschreibende Natur eines
DBS); die Integritätsbedingungen werden vom Datenbank–Designer
definiert und vom DBMS automatisch überprüft;
bei traditioneller File–Verwaltung ist die Datendefinition ein Bestandteil
der Anwendungsprogramme.
Prof. Dr. Dietmar Seipel
12
Vorlesung Datenbanken
Wintersemester 2013/14
Datenunabhängigkeit und Datenabstraktion
Datenmodelle verbergen Details, die (auf höheren Ebenen) nicht von
Interesse sind;
Unterstützung verschiedener Sichten (Views) auf die Daten:
eine Sicht ist eine Teilmenge der Datenbank oder sie besteht aus
virtuellen Daten, welche aus der Datenbank abgeleitet werden, aber
nicht explizit in der Datenbank gespeichert sind.
Datenteilung und Transaktionsverwaltung
Daten von verschiedenen Anwendungen und Benutzern werden in einer
gemeinsamen Datenbank integriert.
Concurrency Control–Mechanismen stellen sicher, daß mehrere
(eventuell parallele) Datenmanipulationen durch unterschiedliche
Benutzer kontrolliert und korrekt abgearbeitet werden können.
Prof. Dr. Dietmar Seipel
13
Vorlesung Datenbanken
Wintersemester 2013/14
Datensicherheit
Backup und Recovery (falls das Computersystem während einer
komplexen Transaktion abstürzt)
Datenschutz
Zugriffskontrolle über Zugriffsrechte
Datenpersistenz
dauerhafte Speicherung von Daten und Programmen als Erweiterung
herkömmlicher Programmiersprachen
Prof. Dr. Dietmar Seipel
14
Vorlesung Datenbanken
Wintersemester 2013/14
Die Drei–Ebenen–Architektur:
externe Ebene
externe Sicht 1
...
externe Sicht n
Views
Abbildung:
extern/konzeptionell
konzeptionelle
Ebene
konzeptionelles Schema
Relationen
Abbildung:
konzeptionell/intern
interne Ebene
gespeicherte
Datenbank
Prof. Dr. Dietmar Seipel
internes Schema
Indexe
Daten
15
Vorlesung Datenbanken
Wintersemester 2013/14
1.1.3 Datenbank–Benutzer
Datenbankadministrator (DBA)
• vergibt Zugriffsrechte auf die Datenbank
• koordiniert und überwacht die Benutzung
• beschafft weitere Soft– und Hardware
• ist verantwortlich für die Systemperformance
Datenbank–Designer
• identifiziert die zu speichernden Daten
• spricht mit allen voraussichtlichen Benutzern
• integriert die Sichten der einzelnen Benutzergruppen
Endbenutzer
erstellt Anfragen, Reports und führt Updates aus
Prof. Dr. Dietmar Seipel
16
Vorlesung Datenbanken
Wintersemester 2013/14
Systemanalytiker und Anwendungsprogrammierer
Systemanalytiker ermitteln die Anforderungen von Endbenutzern und
entwickeln Spezifikationen
Anwendungsprogrammierer implementieren diese Spezifikationen
unterschiedlichste Benutzerschnittstellen
• Anfragesprachen für gelegentliche Benutzer
• Programmiersprachen–Interfaces für Anwendungsprogrammierer
• Formulare und Kommandocodes für parametrische Benutzer
• menügesteuerte oder natürlichsprachliche Schnittstellen für
Einzelbenutzer
Prof. Dr. Dietmar Seipel
17
Vorlesung Datenbanken
Wintersemester 2013/14
Arbeiter hinter den Kulissen
Datenbank–Programmierer
implementieren Module für Systemkatalog, Anfragesprache,
Schnittstellenverwaltung, Datenzugriff, Datensicherheit
Tool–Entwickler
entwickeln Softwarepakete für Datenbankentwurf,
Performance–Überwachung, natürlichsprachliche oder graphische
Schnittstellen, Prototyping, Simulation, Testdatengenerierung
Operateure und Betriebspersonal
verantwortlich für Hardware– und Software–Umgebung des
Datenbanksystems
Prof. Dr. Dietmar Seipel
18
Vorlesung Datenbanken
Wintersemester 2013/14
1.1.4 Vorteile und Nachteile des Datenbankansatzes
Vorteile
• Möglichkeit zur Bildung von Standards in zentralisierter
Datenbankumgebung; dies erleichtert die Kommunikation und
Kooperation zwischen verschiedenen Abteilungen, Projekten und
Benutzern einer großen Organisation.
• verkürzte Entwicklungszeiten für Anwendungen: 15–25% der
Entwicklungszeit verglichen mit der Verwendung von Filesystemen
• Flexibilität: DBMS erlaubt Veränderungen in der Struktur der
Datenbank, ohne die gespeicherten Daten und die existierenden
Anwendungsprogramme zu betreffen
• Einsparungen durch zentrale Aktivitäten zur Datenverarbeitung
Prof. Dr. Dietmar Seipel
19
Vorlesung Datenbanken
Wintersemester 2013/14
Nachteile
• Overhead–Kosten:
Anfangsinvestition in Hardware, Software und Training;
Allgemeinheit eines DBMS zur Definition und Verarbeitung von Daten;
Kosten für Datensicherheit, Concurrency Control, Recovery,
Integritätsüberprüfung
File–Verwaltung ist möglicherweise besser, falls eine der folgenden
Situationen vorliegt:
• die Anwendungen sind einfach, wohldefiniert und nicht dynamisch,
• es gibt strikte Echtzeit–Anforderungen,
• es ist keine Mehrbenutzerfähigkeit erforderlich.
Prof. Dr. Dietmar Seipel
20
Vorlesung Datenbanken
Wintersemester 2013/14
1.2 Das Entity–Relationship–Modell
Das Entity–Relationship–Modell (P.P. Chen, 1976) ist ein universelles
Datenmodell für die Informationsanalyse und den Entwurf des
konzeptionellen Schemas.
1.2.1 Grundbegriffe
Eine Entity ist ein in der realen Welt existierendes und eindeutig
identifizierbares Objekt (z.B. Ding oder Ereignis). Entities werden durch
Eigenschaften (Attribute) repräsentiert.
Entities gleicher Art werden durch Entity–Typen beschrieben und zu
Entity–Mengen zusammengefaßt.
Prof. Dr. Dietmar Seipel
21
Vorlesung Datenbanken
Wintersemester 2013/14
Definition (Entities)
Sei U eine universelle Menge von Attributen, und sei dom(A) der
Wertebereich für A ∈ U .
1. Ein Paar E = (V, K), mit K ⊆ V ⊆ U , ist ein Entity–Typ über der
Attributmenge V und der Menge K von Schlüsselattributen.
2. Eine Entity e vom Typ E = (V, K) ist eine Abbildung, welche jedem
Attribut A ∈ V einen Wert e(A) ∈ dom(A) zuordnet.
Die Projektion e[X] von e auf X ⊆ V ist die Abbildung mit dem
eingeschränkten Definitionsbereich X.
3. Eine Entity–Menge (Instanz) I(E) vom Typ E = (V, K) ist eine Menge
von Entities vom Typ E, die die Schlüsselbedingung erfüllt:
zwei unterschiedliche Entities e, e′ ∈ I(E) können nicht auf K
übereinstimmen ( ∀e, e′ ∈ I(E) : e[K] = e′ [K] =⇒ e = e′ ).
Prof. Dr. Dietmar Seipel
22
Vorlesung Datenbanken
Wintersemester 2013/14
Beispiel (Entity–Typen, Entities)
S TUDENT = ({Name, Stud.Nr., Class, Major}, {Stud.Nr.} )
C OURSE = ({CourseName, C_Nr., CreditHours, Dept.}, {C_Nr.} )
S ECTION = ({Sec.ID., Semester, Year, Instructor}, {Sec.ID} )
Bei der obigen Attribut–Reihenfolge entspricht die folgende Entity st vom
Typ S TUDENT entspricht dem Tupel (Smith, 17, 1, COSC):
st(Name) = Smith,
st(Stud.Nr.) = 17,
st(Class)
st(Major)
= 1,
Name
Stud.Nr.
Class
Major
Smith
17
1
COSC
= COSC.
Die Projektion st[{Name, Stud.Nr.}] entspricht dem eingeschränkten Tupel
(Smith, 17).
Prof. Dr. Dietmar Seipel
23
Vorlesung Datenbanken
Wintersemester 2013/14
Durch die Definition von Entities als Abbildungen wird die Zuordnung von
Attributen und Werten unabhängig von einer Attribut–Reihenfolge.
Entity–Menge I(S TUDENT ) vom Typ S TUDENT:
Name
Stud.Nr.
Class
Major
Smith
17
1
COSC
Brown
8
2
COSC
Entity se vom Typ S ECTION:
SectionIdentifier
Semester
Year
Instructor
112
Fall
2006
Chang
Entity co vom Typ C OURSE:
CourseName
Discrete Mathematics
Prof. Dr. Dietmar Seipel
CourseNumber
CreditHours
Department
MATH2410
3
MATH
24
Vorlesung Datenbanken
Wintersemester 2013/14
Eine Relationship repräsentiert eine Beziehung zwischen Entities zweier oder
mehrerer Entity–Typen; sie kann ebenfalls Eigenschaften haben.
Relationship–Typen beschreiben Relationships gleicher Art,
Relationship–Mengen sind Ausprägungen von Relationship–Typen.
Definition (Relationships)
Seien Ei , 1 ≤ i ≤ n, Entity–Typen mit Entity–Mengen I(Ei ).
1. R = (E1 , . . . , En , V ) heißt Relationship–Typ auf { E1 , . . . , En }.
R heißt binär, falls n = 2, und informationstragend, falls V 6= ∅.
Ein binärer Relationship–Typ mit E1 = E2 heißt rekursiv.
2. Eine Relationship r vom Typ R ist eine Abbildung, welche jedem
Entity–Typ Ei eine Entity r(Ei ) ∈ I(Ei ) und jedem Attribut A ∈ V
einen Wert r(A) ∈ dom(A) zuordnet.
3. Eine Relationship–Menge I(R) vom Typ R ist eine Menge von
Relationships vom Typ R.
Prof. Dr. Dietmar Seipel
25
Vorlesung Datenbanken
Wintersemester 2013/14
Beispiel (Binäre Relationship–Typen)
G RADE _R EPORT = (S TUDENT, S ECTION, {Grade}),
P REREQUISITE = (C OURSE, C OURSE, ∅).
Relationship r vom Typ G RADE _R EPORT:
S TUDENT
S ECTION
Grade
st
se
B
st und se könnten durch ihre Schlüsselattribute StudentNumber = 17 bzw.
SectionIdentifier = 112 repräsentiert werden:
G RADE _R EPORT
StudentNumber
SectionIdentifier
Grade
17
112
B
Der Relationship–Typ P REREQUISITE ist rekursiv.
Prof. Dr. Dietmar Seipel
26
Vorlesung Datenbanken
Wintersemester 2013/14
C OURSE _S ECTION = (C OURSE , S ECTION , ∅).
Relationship r vom Typ C OURSE _S ECTION:
C OURSE
S ECTION
co
se
co und se könnten durch ihre Schlüsselattribute CourseNumber = Math2410
bzw. SectionIdentifier = 112 repräsentiert werden:
C OURSE _S ECTION
Prof. Dr. Dietmar Seipel
CourseNumber
SectionIdentifier
Math2410
112
27
Vorlesung Datenbanken
Wintersemester 2013/14
Definition (Funktionalitätsbedingungen)
1. Ist R = (E1 , E2 , V ) ein binärer Relationship–Typ, so erfüllt eine
Relationship–Menge I(R) vom Typ R die Funktionalitätsbedingung
t ∈ { 1 : 1, 1 : n, n : 1, n : m }, falls für alle r, r ′ ∈ I(R) gilt:
t = 1 : 1:
r(Ei ) = r ′ (Ei ) ⇒ r = r ′ , für i = 1, 2,
t = 1 : n: r(E2 ) = r ′ (E2 ) ⇒ r = r ′ ,
t = n : 1: r(E1 ) = r ′ (E1 ) ⇒ r = r ′ .
2. Für t = n : m ist die Funktionalitätsbedingung eigentlich immer erfüllt.
Oft wird aber die folgende Annahme gemacht, daß es zwischen zwei
Entities höchstens eine Relationship vom Typ R geben kann:
t = n : m: ( r(E1 ) = r ′ (E1 ) ∧ r(E2 ) = r ′ (E2 ) ) ⇒ r = r ′ .
Falls R = (E1 , E2 , V ) die Funktionalitätsbedingung t = 1 : n erfüllt,
so erfüllt R = (E2 , E1 , V ) die Funktionalitätsbedingung t = n : 1.
Prof. Dr. Dietmar Seipel
28
Vorlesung Datenbanken
Wintersemester 2013/14
Beispiel (Funktionalitätsbedingungen)
1. Die beiden folgenden Relationship–Typen sind vom Typ t = n : m:
G RADE _R EPORT
P REREQUISITE
= (S TUDENT, S ECTION, {Grade}),
= (C OURSE, C OURSE, ∅).
2. Der folgende Relationship–Typ ist vom Typ t = 1 : n, da jede S ECTION
zu genau einem C OURSE gehört:
C OURSE _S ECTION = (C OURSE, S ECTION, ∅).
Im relationalen Modell brauchen wir keine Tabelle C OURSE _S ECTION
(siehe oben). Wir nehmen stattdessen das Attribut CourseNumber in
S ECTION auf.
Prof. Dr. Dietmar Seipel
29
Vorlesung Datenbanken
Wintersemester 2013/14
Beispiel (Funktionalitätsbedingungen)
Die Ausprägungen
I(E) = { e1 , . . . , e4 }, I(F ) = { f1 , . . . , f4 },
und die im Bild gezeigte Ausprägung I(R) erfüllen die
Funktionalitätsbedingung t = n : m:
e1
f1
e2
f2
e3
f3
e4
f4
Fast alle Entities e ∈ I(E) – wie z.B. e1 – stehen mit mehreren Entities
f ∈ I(F ) in Beziehung; Analoges gilt für die Entities f ∈ I(F ).
Deswegen erfüllt I(R) die anderen Funktionalitätsbedingungen nicht.
Prof. Dr. Dietmar Seipel
30
Vorlesung Datenbanken
Wintersemester 2013/14
Die Ausprägungen
I(E) = { e1 , . . . , e4 }, I(F ) = { f1 , . . . , f4 },
und die im Bild gezeigte Ausprägung I(R) erfüllen die
Funktionalitätsbedingung t = n : 1:
e1
f1
e2
f2
e3
f3
e4
f4
Alle Entities e ∈ I(E) stehen mit maximal einer Entity f ∈ I(F ) in
Beziehung. e4 , f1 , f4 , stehen mit keiner Entity des anderen Typs in
Beziehung.
Da f2 mit zwei Entities e ∈ I(E) in Beziehung steht, erfüllt I(R) die
Funktionalitätsbedingungen t = 1 : n und t = 1 : 1 nicht.
Prof. Dr. Dietmar Seipel
31
Vorlesung Datenbanken
Wintersemester 2013/14
Funktionalitäten von binären Relationship–Typen
t=1:1
x
x
x
x
x
x
x
x
t=1:n
x
x
x
x
x
x
x
x
t=n:1
x
x
x
x
x
x
x
t=n:m
x
x
x
x
x
x
Prof. Dr. Dietmar Seipel
x
x
x
32
Vorlesung Datenbanken
Wintersemester 2013/14
Binäre und ternäre Relationship–Mengen
EMPLOYEE
WORKS_FOR
e1
r1
e2
r2
e3
e4
e
e
e
...
5
DEPARTMENT
d1
d2
r3
r4
r5
d3
...
SUPPLIER
s1
s2
...
r1
r2
r3
j2
p
r5
j3
...
1
p2
r
r7
...
p3
r
Some instances of the WORKS_FOR relationship
j1
r4
6
r
PROJECT
PART
6
7
SUPPLY
...
6
7
...
The ternary relationship SUPPLY
Prof. Dr. Dietmar Seipel
33
Vorlesung Datenbanken
Wintersemester 2013/14
Definition (ER–Datenbank)
1. Ein ER–Schema ERS = (E, R) besteht aus
• einer Menge E von Entity–Typen und
• einer Menge R von Relationship–Typen auf E.
2. Eine ER–Ausprägung ERI = (I(E), I(R)) für ERS besteht aus
• einer Menge I(E) von Entity–Mengen I(E)
für die Typen E ∈ E und
• einer Menge I(R) von Relationship–Mengen I(R) auf I(E)
für die Typen R ∈ R.
3. Dann ist ERDB = (ERS , ERI ) eine ER–Datenbank.
Prof. Dr. Dietmar Seipel
34
Vorlesung Datenbanken
Wintersemester 2013/14
ER–Diagramme
Entity–Typen
Relationship-Typen
beschreibendes Attribut
Attribute
Schlüsselattribut
Zuordnungen
Prof. Dr. Dietmar Seipel
(von Entity–Typen, Relationship–Typen, Attributen)
35
Vorlesung Datenbanken
Wintersemester 2013/14
Beispiel (ER–Diagramm)
Grade
S TUDENT
n
G RADE _R EPORT
Major
Name
m
S ECTION
Sec.ID.
Class
Inst.
Sem.
Stud.Nr.
n
Year
P REREQUISITE
n
attended
m
C OURSE
required
1
Prof. Dr. Dietmar Seipel
36
Vorlesung Datenbanken
Wintersemester 2013/14
Abbildung ins Relationenmodell
Sowohl Entities als auch Relationships werden in Tabellen (Relationen)
gespeichert.
1. Ein Entity–Typ E = (VE , KE ) mit der Attributmenge
VE = { A1 , . . . , An } und dem Schlüssel KE = { A1 , . . . , Ak },
1 ≤ k ≤ n, wird zu einer Tabelle:
E
A1
...
A1
...
Ak
...
An
Ak
...
An
Prof. Dr. Dietmar Seipel
37
Vorlesung Datenbanken
Wintersemester 2013/14
2. Ein binärer Relationship–Typ R = (E, F, VR ) kann auch als Tabelle
realisiert werden:
E
KE
R
VE′
VR
F
KF
VF′
Entity–Typen:
E = (VE , KE ),
mit dem Schlüssel KE und der weiteren Attributmenge VE′ = VE \ KE .
F = (VF , KF ),
mit KF und VF′ = VF \ KF .
Prof. Dr. Dietmar Seipel
38
Vorlesung Datenbanken
Wintersemester 2013/14
KE
}|
z
A1
...
VR
}|
KF
{z
Ak
}|
B1
...
{z
Bl
V1
...
{
Vh
Schlüssel in der Relationship–Tabelle:
t = 1 : 1 −→ zwei Schlüssel: KE und KF
t = 1 : n −→ ein Schlüssel: KF
t = n : 1 −→ ein Schlüssel: KE
t = n : m −→ ein Schlüssel: KE ∪ KF
kontrollierte Redundanz aus Effizienzgründen manchmal sinnvoll
(z.B. Adresse bei BestellNr. mitführen)
−→ Anfragen schneller, aber Änderungen aufwendiger
Prof. Dr. Dietmar Seipel
39
Vorlesung Datenbanken
Wintersemester 2013/14
3. Ausnahme:
Die n : m–Beziehung E XAM zwischen S TUDENT und T EACHER
erfordert eine Erweiterung des Schlüssels, da ein Student mehrere
Prüfungen bei demselben Dozenten haben kann.
T EACHER
T ID
NAME
n
E XAM
DATE
m
G RADE
S TUDENT
S NR
NAME
Wenn man davon ausgeht, daß ein Student an einem Tag bei demselben
Dozenten maximal eine Prüfung hat, so kann man eine Tabelle zu E XAM
erzeugen mit dem Schlüssel KE XAM = { T ID , S NR, DATE } und dem
weiteren Attribut G RADE.
Prof. Dr. Dietmar Seipel
40
Vorlesung Datenbanken
Wintersemester 2013/14
Im klassischen ER–Modell müßte man stattdessen einen weiteren
Entity–Typ für das Datum mit nur einem einzigen Attribut DATE
einführen. Dann wäre E XAM ein ternärer Relationship–Typ.
4. Alternative für 1 : n–Relationship–Typen:
den Schlüssel KE von E in die Tabelle für F aufnehmen
Beispiele:
• in der U NIVERSITY–Datenbank wurde die 1 : n–Beziehung zwischen
C OURSE und S ECTION durch Aufnahme des Schlüssels CourseNumber
von C OURSE in die Tabelle S ECTION realisiert
• in der C OMPANY–Datenbank (später) wurde die 1 : n–Beziehung
W ORKS _F OR zwischen D EPARTMENT und E MPLOYEE durch Aufnahme
des Schlüssels D NO von D EPARTMENT in die Tabelle E MPLOYEE
realisiert
Prof. Dr. Dietmar Seipel
41
Vorlesung Datenbanken
Wintersemester 2013/14
1.2.2 Erweiterungen des ER–Modells
Ziel: Erhöhung der semantischen Modellierungsfähigkeiten
• Kardinalitätsbedingungen (Verallgemeinerung von Funktionalitäten)
• Existenz–Abhängigkeiten
• schwache Entity–Typen
• höhere semantische Datenmodellierungskonzepte:
– Aggregationshierarchien
– Generalisierungen
Sei h n, m i das Intervall der ganzen Zahlen von n bis m:
h n, m i = { n, n + 1, . . . , m }.
Prof. Dr. Dietmar Seipel
42
Vorlesung Datenbanken
Wintersemester 2013/14
Kardinalitätsbedingung
E
Range(R,E)=<i 1,i 2>
R
Range(R,F)=<i 3,i4 >
F
Sei R = (E, F, V ), und seien I(E), I(F ) Ausprägungen.
Eine Ausprägung I(R) erfüllt die Kardinalitätsbedingung
t = h i1 , i2 i : h i3 , i4 i, falls gilt:
∀e ∈ I(E) : e+ = { r ∈ I(R) | r(E) = e }, | e+ | ∈ h i1 , i2 i,
∀f ∈ I(F ) : f + = { r ∈ I(R) | r(F ) = f }, | f + | ∈ h i3 , i4 i.
Prof. Dr. Dietmar Seipel
43
Vorlesung Datenbanken
Wintersemester 2013/14
Das Intervall Range(R, E) = h i1 , i2 i gibt die minimale bzw. maximale
Anzahl von Relationships r ∈ I(R) an, die eine Entity e ∈ I(E) mit Entities
f ∈ I(F ) haben kann. Die Menge dieser Relationships ist
e+ = { r ∈ I(R) | r(E) = e }.
In der Regel ist | e+ | die Anzahl der Entities f ∈ I(F ), mit denen e in
Beziehung steht. Falls e allerdings mehrere Relationships mit derselben
Entity f ∈ I(F ) hat, dann werden diese separat gezählt.
Analoges gilt für Range(R, F ) = h i3 , i4 i. Die Intervalle geben nur Unter–
und Obergrenzen an, die aber in I(R) in der Regel nicht ausgeschöpft sind.
Im folgenden Beispiel gibt es zwischen zwei Entities ei ∈ I(E) und
fj ∈ I(F ) nur maximal eine Relationship, die wir mit ri,j bezeichnen.
Range(R, F ) = h 0, 4 i ist nicht ausgeschöpft; das maximale | f + | ist 3.
Prof. Dr. Dietmar Seipel
44
Vorlesung Datenbanken
Wintersemester 2013/14
Wir betrachten I(E) = { e1 , . . . , e4 }, I(F ) = { f1 , . . . , f4 } und das im
Bild gezeigte I(R) mit Range(R, E) = h 1, 2 i und Range(R, F ) = h 0, 4 i:
e1
f1
e2
f2
e3
f3
e4
f4
+
+
+
+
+
+
|f4+ | = 0, |e+
3 | = 1, |e1 | = |e2 | = |e4 | = |f1 | = |f3 | = 2, |f2 | = 3 :
Prof. Dr. Dietmar Seipel
e+
1 = { r1,2 , r1,3 },
f1+ = { r2,1 , r4,1 },
e+
2 = { r2,1 , r2,2 },
f2+ = { r1,2 , r2,2 , r4,2 },
e+
3 = { r3,3 },
f3+ = { r1,3 , r3,3 },
e+
4 = { r4,1 , r4,2 },
f4+ = { }.
45
Vorlesung Datenbanken
Wintersemester 2013/14
Bemerkung (Funktionalitäts– vs. Kardinalitätsbedingung)
Die größere Zahl und das korrespondierende größere Intervall stehen auf
entgegengesetzten Seiten:
1:1
≡
h 0, 1 i : h 0, 1 i,
1:n
≡
h 0, ∞ i : h 0, 1 i,
n:1
≡
h 0, 1 i : h 0, ∞ i,
n:m
≡
h 0, ∞ i : h 0, ∞ i.
Kardinalitätsbedingungen müssen beim Update der entsprechenden
Relationen überprüft werden.
Prof. Dr. Dietmar Seipel
46
Vorlesung Datenbanken
Wintersemester 2013/14
Existenzabhängigkeit
t = h i1 , i2 i : h 1, 1 i
Jede Ziel–Entity f ∈ I(F ) muß mit genau einer Quellentity e ∈ I(E) über R
in Beziehung stehen.
E
Range(R,E)=<i 1,i 2>
R
Range(R,F)=<1,1>
F
Beispiel: Eine Order kann nur existieren, wenn es einen Customer dazu gibt.
Order
Prof. Dr. Dietmar Seipel
<1,1>
Order_for_Customer
<0,
>
Customer
47
Vorlesung Datenbanken
Wintersemester 2013/14
Existenzabhängigkeiten sollten möglichst nur Hierarchien bilden (keine
Zyklen).
E1
ED: existence dependency
ED
ED
E2
E4
ED
ED
E3
Prof. Dr. Dietmar Seipel
E5
ED
E6
48
Vorlesung Datenbanken
Wintersemester 2013/14
Schwache Entity–Typen
Die bekannte Schlüsselbedingung heißt auch globale oder starke
Schlüsselbedingung. Ein Entity–Typ mit globaler Schlüsselbedingung heißt
auch starker Entity–Typ. Sein Schlüssel heißt auch globaler Schlüssel.
Ein schwacher Entity–Typ F tritt zusammen mit einem definierenden
1:n–Relationship–Typ R = (E, F, V ) und einer Existenzabhängigkeit auf:
• Jede schwache Entity f von Typ F muß mit genau einer Entity e vom
Entity–Typ E in Beziehung stehen.
• Der Schlüsselwert von f ist nur lokal eindeutig innerhalb aller Entities
von Typ F , die mit diesem e in Beziehung stehen.
• Der global eindeutige Schlüssel ergibt sich erst durch Verkettung der
Schlüssel von e und f .
Prof. Dr. Dietmar Seipel
49
Vorlesung Datenbanken
Wintersemester 2013/14
Beispiel (Übungsgruppen)
K_Nr.
K URSE
1
n
G RUPPEN
Name
Gr_Nr.
Raum
K1
K2
K3
G1 G2 G3
G1 G2
G1
K1 : ADS, Gruppe 1–3
K2 : Logik, Gruppe 1–2
K3 : Softwaretechnik, Gruppe 1
Zeit
Die gleiche Gruppennummer ist für unterschiedliche Kurse sinnvoll.
Die Gruppennummer ist lokal eindeutig bezüglich eines Kurses.
Die globale Eindeutigkeit wird durch die Verbindung der Kursnummer und
der Gruppennummer erzielt.
Prof. Dr. Dietmar Seipel
50
Vorlesung Datenbanken
Wintersemester 2013/14
Relationale Repräsentation:
G RUPPEN
K URSE
K_Nr.
Name
K1
ADS
K2
Logik
K3
Softwaretechnik
K_Nr.
Gr_Nr.
Raum
Zeit
K1
G1
...
...
K1
G2
K1
G3
K2
G1
K2
G2
K3
|
G1
| {z }
lokaler S.
{z
}
globaler S.
Schwache Schlüsselbedingungen können ebenfalls nur Hierarchien bilden.
Prof. Dr. Dietmar Seipel
51
Vorlesung Datenbanken
Wintersemester 2013/14
Definition (Schwacher Entity–Typ)
Sei E = (V1 , K1 ) ein starker Entity–Typ mit globalem Schlüssel K1 und
F = (V2 , K2 ) ein weiterer Entity–Typ, sowie R = (E, F, V ) ein
Relationship–Typ, so daß F existenzabhängig ist von E bezüglich R.
1. F heißt schwacher Entity–Typ, g.d.w. für alle Ausprägungen
I(E), I(F ), I(R) die folgende schwache Schlüsselbedingung gilt:
für alle r, r ′ ∈ I(R):
( r(E) = r ′ (E) ∧ r(F )[K2 ] = r ′ (F )[K2 ] ) =⇒ r(F ) = r ′ (F ).
2. K2 heißt lokaler Schlüssel von F .
K1 ∪ K2 heißt globaler Schlüssel von F .
3. Für r ∈ I(R) und e = r(E), f = r(F ), heißt e[K1 ] vererbter
Schlüsselwert von f .
Prof. Dr. Dietmar Seipel
52
Vorlesung Datenbanken
Wintersemester 2013/14
Relationale Repräsentation:
Da insbesondere ein 1:n–Relationship–Typ R = (E, F, V ) vorliegt,
wird der Schlüssel K1 von E in die Relation für F integriert.
Also erhalten wir zwei Relationen:
• Der starke Entity–Typ E = (V1 , K1 ) wird – wie gewohnt – zu einer
Relation mit der Attributmenge V1 und dem Schlüssel K1 .
• Der schwache Entity–Typ F = (V2 , K2 ) wird zu einer Relation mit der
Attributmenge V2 ∪ K1 und dem Schlüssel K2 ∪ K1 .
Durch die Vereinigung mit dem vererbten Schlüssel K1 wird der lokale
Schlüssel K2 zu einem globalen Schlüssel K2 ∪ K1 .
Der vererbte Schlüssel K1 realisiert die 1:n–Relationship zwischen den
Entities der Typen E und F .
Prof. Dr. Dietmar Seipel
53
Vorlesung Datenbanken
Wintersemester 2013/14
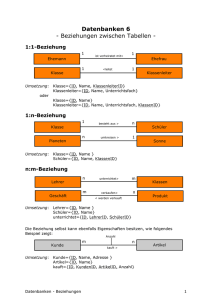
Zusammenfassung der ER–Symbole
Symbol
Bedeutung
Entity-Typ
schwacher Entity-Typ
Relationsip-Typ
identifizierender Relationship-Typ
Attribut
Schlüsselattribut
mehrwertiges Attribut
...
zusammengesetzes Attribut
abgeleitetes Attribut
E
E
R
1
R
Prof. Dr. Dietmar Seipel
R
N
(min,max)
F
zu jedem Element aus F muß es mindestens eines aus E geben
F
1:N -Beziehung zwischen E und F
E
Constraint (min,max)
54
Vorlesung Datenbanken
Wintersemester 2013/14
1.2.3 Beispiel: die C OMPANY–Datenbank
Die C OMPANY–Datenbank enthält folgende Entity–Typen:
• Angestellte (E MPLOYEE) und deren Angehörige (D EPENDENT),
• Abteilungen (D EPARTMENT), sowie
• Projekte (P ROJECT).
Die Relationship–Typen repräsentieren folgende Beziehungen dazwischen:
• Für alle Angestellten gibt S UPERVISION den Vorgesetzten und
D EPENDENTS _O F die Angehörigen an.
Der schwache Entity–Typ D EPENDENT wird durch den
Relationship–Typ D EPENDENTS _O F und den Entity–Typ E MPLOYEE
eindeutig gemacht.
Prof. Dr. Dietmar Seipel
55
Vorlesung Datenbanken
Wintersemester 2013/14
• Für alle Abteilungen gibt W ORKS _F OR die zugehörigen Angestellten
und M ANAGES den Manager an.
Die Funktionalitäten und die Existenzabhängigkeiten sagen zusammen
aus, daß jeder Angestellte in genau einer Abteilung sein und daß jede
Abteilung Angestellte und genau einen Manager haben muß;
außerdem kann ein Angestellter maximal eine Abteilung managen.
• Für alle Projekte gibt W ORKS _O N die beteiligten Angestellten und
C ONTROLS die verantwortlichen Abteilungen an.
Die Funktionalitäten und die Existenzabhängigkeiten sagen zusammen
aus, daß jeder Angestellte an einem Projekt beteiligt sein und daß jedes
Projekt Angestellte und genau eine verantwortliche Abteilung haben
muß.
Prof. Dr. Dietmar Seipel
56
Vorlesung Datenbanken
Wintersemester 2013/14
Minit
LName
FName
Adress
Number
WORKS_FOR
1
N
Name
Salary
Locations
Sex
Name
Startdate
SSN
NumberOfEmployees
DEPARTMENT
EMPLOYEE
1
1
MANAGES
BDate
1
CONTROLS
Hours
supervisor
M
supervisee
1
1
SUPERVISION
N
N
RROJECT
WORKS_ON
N
DEPENDENTS_OF
Location
Name
Number
N
DEPENDENT
Relationship
Name
Sex
Prof. Dr. Dietmar Seipel
BirthDate
57
Vorlesung Datenbanken
Wintersemester 2013/14
In E MPLOYEE werden die Komponenten des zusammengesetzten Attributs
NAME aus dem ER–Diagramm zu 3 eigenständigen Attributen.
Die 1:n–Relationship–Typen W ORKS _F OR und S UPERVISION werden als
Fremdschlüssel DNO bzw. SUPERSSN in E MPLOYEE integriert.
E MPLOYEE
FNAME
MINIT
LNAME
SSN
BDATE
ADDRESS
SEX
SALARY
SUPERSSN
DNO
John
B
Smith
444444444
1955-01-09
731 Fondren, Houston, TX
M
30000
222222222
5
Franklin
T
Wong
222222222
1945-12-08
638 Voss, Houston, TX
M
40000
111111111
5
Alicia
J
Zelaya
777777777
1958-07-19
3321 Castle, Spring, TX
F
25000
333333333
4
Jennifer
S
Wallace
333333333
1931-06-20
291 Berry, Bellaire, TX
F
43000
111111111
4
Ramesh
K
Narayan
555555555
1952-09-15
975 Fire Oak, Humble, TX
M
38000
222222222
5
Joyce
A
English
666666666
1962-07-31
5631 Rice, Houston, TX
F
25000
222222222
5
Ahmad
V
Jabbar
888888888
1959-03-29
980 Dallas, Houston, TX
M
25000
333333333
4
James
E
Borg
111111111
1927-11-10
450 Stone, Houston, TX
M
55000
NULL
1
Prof. Dr. Dietmar Seipel
58
Vorlesung Datenbanken
Wintersemester 2013/14
Die Abteilungen, die Angestellten und deren Vorgesetzte:
Headquarters
111111111
1: James Borg
Research
444444444
5: John Smith
Prof. Dr. Dietmar Seipel
Administration
j
222222222
5: Franklin Wong
333333333
4: Jennifer Wallace
?
555555555
5: Ramesh Narayan
j
666666666
5: Joyce English
777777777
4: Alicia Zelaya
R
888888888
4: Ahmad Jabbar
59
Vorlesung Datenbanken
Wintersemester 2013/14
Der 1:1–Relationship–Typ M ANAGES wird als Fremdschlüssel MGRSSN
zusammen mit dem beschreibenden Attribut MGRSTARTDATE in
D EPARTMENT integriert.
Das mehrwertige Attribut Locations des Entity–Typs D EPARTMENT führt zu
einer eigenen Tabelle D EPT _L OCATIONS.
D EPT _L OCATIONS
D EPARTMENT
DNUMBER
DLOCATION
DNAME
DNUMBER
MGRSSN
MGRSTARTDATE
1
Houston
Headquarters
1
111111111
1971-06-19
4
Stafford
Administration
4
333333333
1985-01-01
5
Bellaire
Research
5
222222222
1978-05-22
5
Sugarland
5
Houston
Prof. Dr. Dietmar Seipel
60
Vorlesung Datenbanken
Wintersemester 2013/14
W ORKS _O N
ESSN
PNO
HOURS
111111111
20
NULL
222222222
2
10.0
222222222
3
10.0
333333333
10
333333333
20
15.0
777777777
20
Houston
333333333
30
20.0
444444444
1
32.5
888888888
30
Stafford
444444444
2
7.5
222222222
1
Bellaire
555555555
3
40.0
666666666
1
20.0
444444444
2
Sugarland
666666666
2
20.0
555555555
3
777777777
10
10.0
777777777
30
30.0
888888888
10
35.5
888888888
30
5.0
Prof. Dr. Dietmar Seipel
111111111
666666666
61
Vorlesung Datenbanken
Wintersemester 2013/14
Der 1:n–Relationship–Typ C ONTROLS zwischen D EPARTMENT und
P ROJECT wird als Fremdschlüssel DNUM in P ROJECT integriert.
P ROJECT
PNAME
PNUMBER
PLOCATION
DNUM
ProductX
1
Bellaire
5
ProductY
2
Sugarland
5
ProductZ
3
Houston
5
Computerization
10
Stafford
4
Reorganization
20
Houston
1
Newbenefits
30
Stafford
4
Jedes Projekt ist an einem der Standorte der kontrollierenden Abteilung.
Prof. Dr. Dietmar Seipel
62
Vorlesung Datenbanken
Wintersemester 2013/14
Der schwache Entity–Typ D EPENDENT wird durch den Fremdschlüssel
ESSN, der sich auf den Schlüssel SSN des Entity–Typs E MPLOYEE bezieht,
eindeutig.
D EPENDENT
Prof. Dr. Dietmar Seipel
ESSN
D EPENDENT _NAME
SEX
BDATE
RELATIONSHIP
222222222
Alice
F
1976-04-05
DAUGHTER
222222222
Theodore
M
1973-10-25
SON
222222222
Joy
F
1948-05-03
SPOUSE
333333333
Abner
M
1932-02-29
SPOUSE
444444444
Michael
M
1978-01-01
SON
444444444
Alice
F
1978-12-31
DAUGHTER
444444444
Elizabeth
F
1957-05-05
SPOUSE
63
Vorlesung Datenbanken
Wintersemester 2013/14
EMPLOYEE
FNAME
MINIT
LNAME
SSN
BDATE
ADDRESS
SEX
SALARY
SUPERSSN
DNO
DEPARTMENT
DNAME
DNUMBER
MGRSSN
MGRSTARTDATE
DEPT_LOCATIONS
DNUMBER
DLOCATION
PROJECT
PNAME
PNUMBER
PLOCATION
DNUM
WORKS_ON
ESSN
PNO
HOURS
DEPENDENT
ESSN
DEPENDENT_NAME
SEX
BDATE
RELATIONSHIP
Referential integrity constraints displayed on the COMPANY relational database schema
Prof. Dr. Dietmar Seipel
64