Definition (Peano-Axiome): Eine Menge Õ heißt Menge der

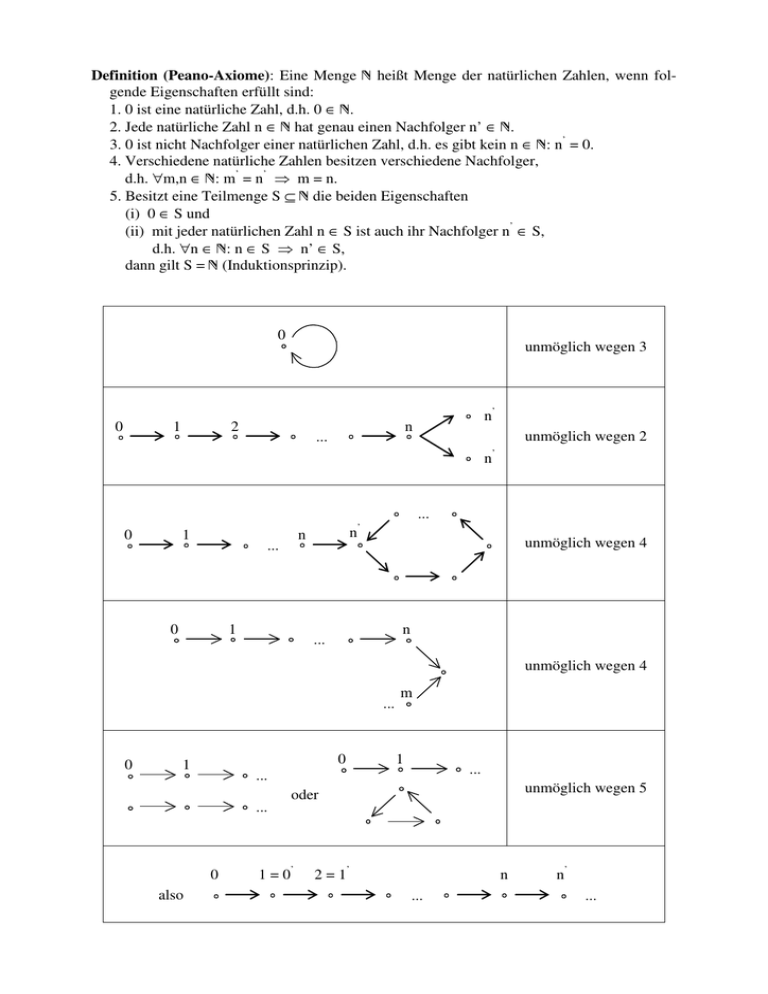
Definition (Peano-Axiome): Eine Menge Õ heißt Menge der natürlichen Zahlen, wenn folgende Eigenschaften erfüllt sind:
1. 0 ist eine natürliche Zahl, d.h. 0 ∈ Õ.
2. Jede natürliche Zahl n ∈ Õ hat genau einen Nachfolger n’ ∈ Õ.
3. 0 ist nicht Nachfolger einer natürlichen Zahl, d.h. es gibt kein n ∈ Õ: n’ = 0.
4. Verschiedene natürliche Zahlen besitzen verschiedene Nachfolger,
d.h. ∀m,n ∈ Õ: m’ = n’ ⇒ m = n.
5. Besitzt eine Teilmenge S ⊆ Õ die beiden Eigenschaften
(i) 0 ∈ S und
(ii) mit jeder natürlichen Zahl n ∈ S ist auch ihr Nachfolger n’ ∈ S,
d.h. ∀n ∈ Õ: n ∈ S ⇒ n’ ∈ S,
dann gilt S = Õ (Induktionsprinzip).
0
0
1
unmöglich wegen 3
2
n’
n
...
unmöglich wegen 2
n
’
...
0
1
0
n
n
...
1
’
unmöglich wegen 4
n
...
unmöglich wegen 4
...
0
0
1
1
...
...
...
0
also
m
unmöglich wegen 5
oder
1 = 0’
2 = 1’
n
...
n’
...