Beweis Strahlensatz

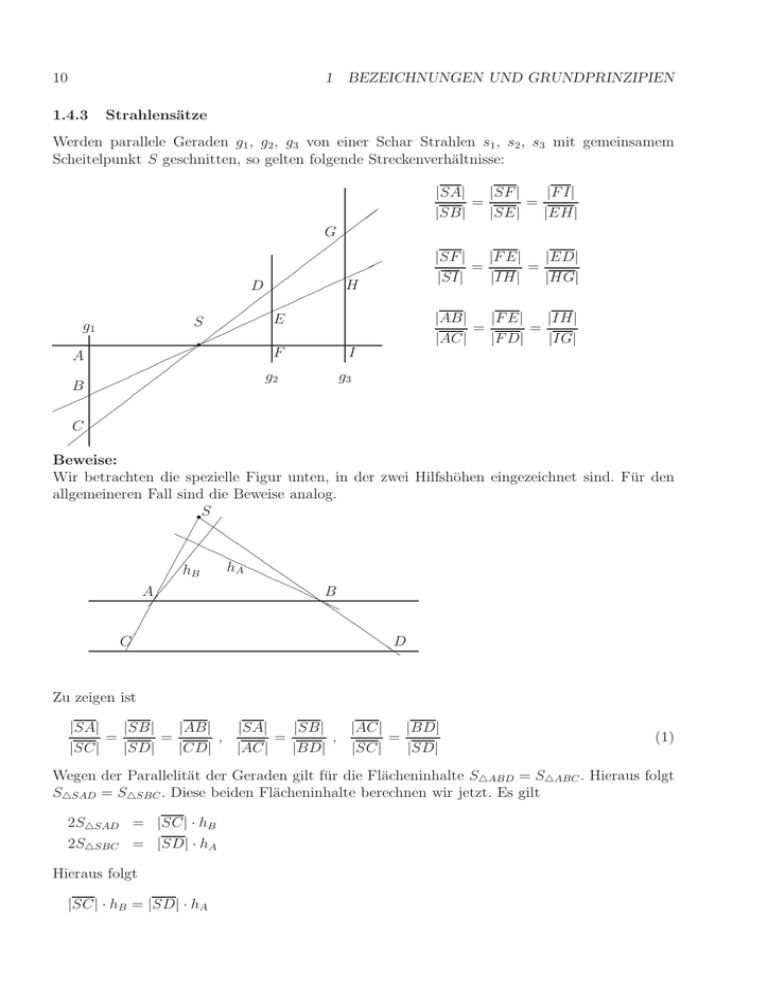
10
1 BEZEICHNUNGEN UND GRUNDPRINZIPIEN
1.4.3
Strahlensätze
Werden parallele Geraden g1 , g2 , g3 von einer Schar Strahlen s1 , s2 , s3 mit gemeinsamem
Scheitelpunkt S geschnitten, so gelten folgende Streckenverhältnisse:
,
,
,
G,
,
,
,
,
H
D ,
,
, , E
S ,
g1
,
r
,
F
I
,
A
,
,
g2
g3
B ,,
,
,
C,,
,
|SA|
|SF |
|F I|
=
=
|SB|
|SE|
|EH|
|F E|
|ED|
|SF |
=
=
|SI|
|IH|
|HG|
|AB|
|F E|
|IH|
=
=
|AC|
|F D|
|IG|
Beweise:
Wir betrachten die spezielle Figur unten, in der zwei Hilfshöhen eingezeichnet sind. Für den
allgemeineren Fall sind die Beweise analog.
rS
Z
HH ZZ
HH Z
HHZ
hA HZ
h
B
HZ
HZ
HZ B
A
HH
ZH
Z
Z
Z
Z D
C
ZZ
Zu zeigen ist
|SA|
|SB|
|AB|
|SA|
|SB|
|AC|
|BD|
=
=
,
=
,
=
|SC|
|SD|
|CD|
|AC|
|BD|
|SC|
|SD|
(1)
Wegen der Parallelität der Geraden gilt für die Flächeninhalte S△ABD = S△ABC . Hieraus folgt
S△SAD = S△SBC . Diese beiden Flächeninhalte berechnen wir jetzt. Es gilt
2S△SAD = |SC| · hB
2S△SBC = |SD| · hA
Hieraus folgt
|SC| · hB = |SD| · hA
11
1.4 Streckenverhältnisse, Strahlensätze
Außerdem gilt (Flächeninhalt von △SAB berechnet auf zwei verschiedene Weisen)
2S△SAB = |SA| · hB = |SB| · hA
Dividiert man beide Gleichungen folgt
|SA|
|SB|
=
|SC|
|SD|
Das ist die erste Gleichung
Aus |SC| = |SA| + |AC| und |SD| = |SB| + |BD| folgt
|SA|
|SB|
=
|AC|
|BD|
|AC|
|BD|
=
|SC|
|SD|
und
Das sind die dritte und vierte Gleichung.
Zum Beweis der zweiten Gleichung drehen wir die Figur und ziehen eine Parallele zu SD durch
A. Der Schnittpunkt dieser Parallelen mit CD sei A′ . Es ist |AB| = |A′ D|, weil die beiden
Parallelenpaare ein Parallelogramm bilden, bei dem gegenüberliegende Seiten gleich lang sind.
Nach der bereits bewiesenen vierten Gleichung aus (5) gilt nun
|SA|
|A′ D|
|AB|
=
=
|SC|
|CD|
|CD|
Das ist die zweite Gleichung aus (5).
1.4.4
Ähnliche Dreiecke
Zwei Dreiecke sind ähnlich, falls sie in zwei (und damit auch in drei) Winkeln übereinstimmen.
Bringt man die Dreiecke in Ähnlichkeitslage, d.h. legt man zwei gleiche Winkel (z.B. α) übereinander, folgt aus der Umkehrung des Wechselwinkelsatzes, daß die Dreiecksseiten parallel sind.
Damit gelten folgende Beziehungen:
C r
B
γB
α
r
A
r ′
BC
γB
B
B
B
B
B
B
B
B
B
B
β BBr
B
B
|AB|
|BC|
|CA|
= ′ ′ = ′
′
|AB |
|B C |
|C A|
B
B
B
B
|AB|
|AB ′ |
|AB|
|AB ′ |
=
,
=
, ...
|AC|
|AC ′ |
|BC|
|BC ′ |
B
B
βB
Br
′
|AB| : |BC| : |CA| = |AB ′ | : |B ′ C ′ | : |C ′ A|
B
B
Liegen die Winkel α übereinander, aber das Dreieck △ABC ist bezüglich der Winkelhalbierenden des Winkels α gespiegelt, sind im allgemeinen BC und B ′ C ′ nicht mehr parallel. Aber in
diesem Fall ist das Viereck 2BCB ′ C ′ ein Sehnenviereck.