Einführungsvorlesung: Optische Wellenleiter

Einführungsvorlesung:
Optische Wellenleiter
Priv.-Doz. Dr. Axel Pelster
1. Strahlenoptik
2. Wellenoptik
2.1. Dielektrischer Wellenleiter
2.2. Stufenfaser
Optische Wellenleiter
Axel Pelster
1
Lichtwellenleiter
(siehe D. Meschede: Optik, Licht und Laser)
Optische Wellenleiter
Axel Pelster
2
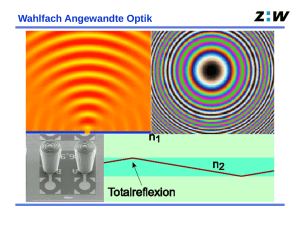
Grundprinzip
Maximaler Einfallwinkel:
n0 sin αc =
p
γ > γc = arcsin (n2/n1)
Totalreflexion:
n21 − n22 = NA
Typische Zahlenwerte:
n0 = 1 , n1 = n2 +0.015 , n2 = 1.45
Optische Wellenleiter
=⇒
γc = 81.8◦ , αc = 12.1◦
Axel Pelster
3
Frequenzbandbreite
Abschätzung:
sa = c t
sa
total reflektierter Strahl:
st =
= c (t + ∆t) > sa
sin βc
1
c n2
sa = 1 km
=⇒
∆ν =
=
=⇒
∆ν = 30 MHz
∆t sa(n1 − n2)
axialer Strahl:
größeres n ,
kleineres c0/n
∆ν = 106 MHz
Gradientenindex-Wellenleiter:
kleineres n ,
größeres c0/n
Optische Wellenleiter
Axel Pelster
4
Maxwell-Gleichungen in Materie
gegeben:
ρ(r, t) , j(r, t)
gesucht:
D(r, t) , E(r, t) ;
B(r, t) , H(r, t)
(M1)
div D(r, t) = ρ(r, t)
(M2)
div B(r, t) = 0
(M3)
(M4)
∂B(r, t)
rot E(r, t) = −
∂t
∂D(r, t)
rot H(r, t) = j(r, t) +
∂t
Materialgleichungen:
D(r, t) , H(r, t) ⇐⇒ E(r, t) , B(r, t)
Optische Wellenleiter
Axel Pelster
5
Maxwell-Gleichungen in Dielektrika
Keine Ladungen und Ströme:
ρ(r, t) = 0 , j(r, t) = 0
Materialgleichungen:
D(r, t) = 0r (r) E(r, t) ,
(M1)
(M2)
B(r, t) = µ0µr (r) H(r, t) ,
µr (r) = 1
grad r (r)
div E(r, t) = −
E(r, t)
r (r)
div H(r, t) = 0
(M3)
∂H(r, t)
rot E(r, t) = −µ0
∂t
(M4)
∂E(r, t)
rot H(r, t) = 0r (r)
∂t
Elektromagnetische Wellen?
Optische Wellenleiter
Axel Pelster
6
Wellengleichungen in Dielektrika
h
i h
i
rot rot E(r, t) = grad div E(r, t) − div grad E(r, t)
(M1)
= −grad
grad r (r)
E(r, t) − ∆ E(r, t)
r (r)
(M3),(M4) r (r) ∂ 2E(r, t)
,
=
− 2
2
c0
∂t
=⇒
Analoge
Herleitung:
=⇒
1
c0 = √
0 µ 0
2
grad r(r)
r (r) ∂
− ∆ E(r, t) = grad
E(r, t)
c20 ∂t2
r(r)
2
r (r) ∂
grad r(r)
−
∆
H(r,
t)
=
× H(r, t)
2
2
c0 ∂t
r(r)
Vernachlässigung der Korrektur zur Wellengleichung
Optische Wellenleiter
Axel Pelster
7
Dielektrische Wellenleiter
Propagierende Welle:
E(r, t) = E(x, y) ei(kz−ωt)
H(r, t) = H(x, y) ei(kz−ωt)
2
∂
∂2
ω2
E(x, y)
0
2
+
+
(x,
y)
−
k
=
r
H(x, y)
0
∂x2 ∂y 2 c20
Zerlegung der Felder:


Ex(x, y)


E⊥(x, y) = Ey (x, y)  ,
0


Hx(x, y)


H⊥(x, y) = Hy (x, y)  ,
0
Optische Wellenleiter


0


Ek(x, y) =  0

Ez (x, y)


0


Hk(x, y) = 
0

Hz (x, y)
Axel Pelster
8
Transversale Felder
Konsequenz von (M3), (M4):
E⊥(x, y) =
ik∇ Ez (x, y) − iωµ0 (ez × ∇) Hz (x, y)
k02 r (x, y) − k 2
H⊥(x, y) =
ik∇ Hz (x, y) + iω0r (x, y) (ez × ∇) Ez (x, y)
k02 r (x, y) − k 2
(siehe J.D. Jackson: Klassische Elektrodynamik)
Helmholtz-Gleichungen für z-Komponenten:
2
2
∂
∂
2
2 2
n
(x,
y)
−
k
+
+
k
0
∂x2 ∂y 2
Betrag des Wellenvektors im Vakuum:
Brechungsindex:
Optische Wellenleiter
Ez (x, y)
Hz (x, y)
0
=
0
k0 = ω/c0
p
n(x, y) = r (x, y)
Axel Pelster
9
Analogie zur Quantenmechanik
Quantenmechanik in D = 2
Dielektrischer Wellenleiter
h
i
2 2
2
∆⊥ + k0 n (x, y) − k Ez (x, y) = 0

iff
2M h
∆⊥ − 2 V (x, y) − E
ψ(x, y) = 0
~
2M
− 2 V (x, y)
~
k02 n2 (x, y)
−k
2M
E
~2
2
ausbreitungsfähige Mode: k reell
gebundene Lösung: E < 0
gedämpfte Mode: k imaginär
Streulösung: E > 0
=⇒
Übertragung von Lösungsmethoden
Optische Wellenleiter
Axel Pelster
10
Stufenfaser
Zylindersymmetrie:
Hz (r, ϕ) = hl (r) eilϕ
2
2
1 ∂
∂
l
el(r)
0
2
2 2
=
+
− + k0 n (r) − k
hl (r)
0
∂r 2 r ∂r r 2
Ez (r, ϕ) = el (r) eilϕ ,
Spezialisierung:
"
"
2
2
1 ∂
l
∂
2
2
+
+
k
−
−
k
1
∂r 2
r ∂r
r2
2
2
1 ∂
l
∂
2
2
+
+
k
−
−
k
2
∂r 2
r ∂r
r2
Optische Wellenleiter
#
#
el (r)
hl (r)
!
el (r)
hl (r)
!
=
=
0
0
!
,
0 ≤ r ≤ a,
0
0
!
,
r ≥ a,
k 1 = k 0 n1
k 2 = k 0 n2
Axel Pelster
11
Helmholtz-Gleichung im Kern
2
k⊥
= k12 − k 2 > 0
Bedingung für geführte Welle:
X = k⊥ r
Dimensionslose Koordinate:
=⇒
2
2
l
∂
1 ∂
+
1
−
+
∂X 2 X ∂X
X2
el(X)
hl (X)
0
=
,
0
0 ≤ X ≤ k⊥ a
Besselsche Differentialgleichung erster Gattung
Bessel-Funktionen
Al
el (X)
=
Jl (X) ,
hl(X)
Bl
Optische Wellenleiter
Weber-Funktionen
0 ≤ X ≤ k⊥ a
Axel Pelster
12
Helmholtz-Gleichung im Mantel
Bedingung für evaneszente Welle:
κ2 = k 2 − k22 > 0
Dimensionslose Koordinate:
Y = κr
=⇒
2
2
∂
l
1 ∂
−
1
−
+
∂Y 2 Y ∂Y
Y2
el(Y )
hl (Y )
0
=
,
0
Y ≥ κa
Besselsche Differentialgleichung zweiter Gattung
Modifizierte Bessel-Funktionen
Macdonald-Funktionen
Cl
el(Y )
=
Kl(Y ) ,
Y ≥ κa
hl (Y )
Dl
Optische Wellenleiter
Axel Pelster
13
Randbedingungen
=0
n
(M2)
n (H2 − H1) = 0
(M3)
n × (E2 − E1) = 0
(M4)
n × (H2 − H1) = 0
−
n21 E1
(M1)
Zylindersymmetrie:
Optische Wellenleiter
n22 E2
Dielektrische Wellenleiter:
n = er
(M1)
n22 E2,r = n21 E1,r
(M2)
H2,r = H1,r
(M3)
E2,ϕ = E1,ϕ ,
E2,z = E1,z
(M4)
H2,ϕ = H1,ϕ ,
H2,z = H1,z
Axel Pelster
14
Einarbeitung der Randbedingungen
Stetigkeit der z-Komponente:
el (r)
hl (r)
=
=
8
Jl (X)
>
>
A
>
< l J (X ) ,
l
0 ≤ X = k⊥r ≤ Xa = k⊥a
a
>
Kl (Y )
>
>
,
: Al
Kl(Ya )
8
Jl (X)
>
>
>
<Bl J (X ) ,
l
a
>
Kl(Y )
>
>
B
,
: l
Kl (Ya )
Y = κr ≥ Ya = κa
0 ≤ X = k⊥r ≤ Xa = k⊥a
Y = κr ≥ Ya = κa
Stetigkeit der ϕ-Komponente:
»
–
»
0
1
1
−il
+
Xa2
Ya2
=⇒
Charakteristische Gleichung
B
B
B
"
#
B
2
0
2 0
n K (Ya)
@ 0ω n1Jl (Xa )
+ 2 l
k
XaJl (Xa )
YaKl (Ya)
Optische Wellenleiter
µ0ω
k
Jl0(Xa )
Kl0(Ya )
+
Xa Jl (Xa )
YaKl (Ya )
–
»
1
1
+ 2
il
Xa2
Ya
–1
C
C
C
C
A
Al
Bl
!
=
Axel Pelster
0
0
15
!
Schwach Führende Wellenleiter
Vereinfachung:
n1 − n2
1
=⇒
k1 ≈ k ≈ k2
n1
Jl0(Xa)
1
Kl0 (Ya)
1
+
= ±l
+
XaJl (Xa) YaKl(Ya)
Xa2 Ya2
∆=
=⇒
(1)
Nebenbedingung:
Xa2
+
Ya2
=
a2k02
n21
−
n22
= ak0 NA
2
=V2
(2)
Bilanz:
(1) + (2):
=⇒
=⇒
Xa,lm , Ya,lm ; l = 0, 1, 2, . . . ; m = 1, 2, 3, . . .
Betrag des Wellenvektors:
Optische Wellenleiter
klm
Axel Pelster
16
Transversale Moden (l = 0)
TM-Mode:
A0 6= 0 ,
B0 = 0
TE-Mode:
A0 = 0 ,
B0 6= 0
√
√
2
2
XJ0 (X)
V − X K0 ( V 2 − X 2 )
=
−
√
2 − X 2)
J1(X)
K
(
V
1
|
{z
}
{z
}
|
Bedingung:
V = ak0 NA ≥ VG = X1 ≈ 2.4048 ,
=⇒
ω ≥ ωG =
Optische Wellenleiter
2.4048 c0
,
a NA
J0(X1) = 0
λ0 ≤ λG =
2π NA
a
2.4048
Axel Pelster
17
Hybrid-Moden (l ≥ 1)
HE1 :
HEl-Moden
EHl-Moden
XJl(X)
Y Kl (Y )
−
=0
Jl−1(X) Kl−1(Y )
XJl(X) Y Kl (Y )
+
=0
Jl+1(X) Kl+1(Y )
√
√
2
2
XJ1 (X)
V − X K1 ( V 2 − X 2 )
=
√
2 − X 2)
J0 (X)
K
(
V
0
| {z }
{z
}
|
√
√
XJ1 (X)
V 2 − X 2 K1 ( V 2 − X 2 )
EH1 : −
=
√
J2(X)
K2 ( V 2 − X 2 )
|
{z
}
|
{z
}
Monomoden-Wellenleiter (HE11):
NA = 0.12 , λG = 800 nm
Optische Wellenleiter
=⇒
2π NA
λ0 ≥ λG =
a
2.4048
a=
2.4048
λG = 2.55 µm
2π NA
Axel Pelster
18
Intensitätsverteilung (E-Feld)
HE11
HE21
HE12
TE01
Optische Wellenleiter
Axel Pelster
19