Aufgaben - IAP TU

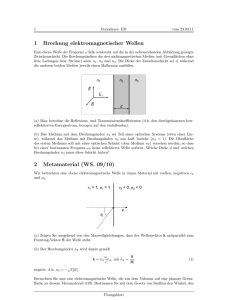
Übungen zur Vorlesung
Blatt 10
9.1.2007
Theoretische Physik III:
Theorie klassischer Teilchen und Felder II
Prof. Dr. G. Alber
Dipl.-Phys. O. Kern
1. Eine ebene monochromatische elektromagnetische Welle trifft unter einem beliebigen Einfallswinkel α von einem Isolator (ε1 , µ1) kommend auf die ebene Grenzfläche zu einem Leiter (ε2 =
i ωσ , µ2 = 1).
(a) Bestimmen Sie die Winkel γ und β der reflektierten und transmittierten Welle. Spezialisieren
Sie das Brechungsgesetz auf den Fall eines guten Leiters (ε1 µ1 ≪ ωσ ) und eines schlechten
Leiters (ε1 µ1 sin2 α ≫ ωσ ).
(b) Bestimmen Sie die entsprechende Lösung der Maxwellschen Gleichungen für den transversal
elektrischen Fall. Gibt es einen Einfallswinkel, für den es keinen reflektierten Anteil gibt ?
(c) Berechnen Sie dass zeitlich gemittelte Poyntingsche Vektorfeld für den im Isolator reflektierten und den in den Leiter eintringenden Anteil der monochromatischen ebenen Welle aus b.
Wie groß ist die mittlere Eindringtiefe in den Leiter ? In welche Richtung wird im Leiter die
Feldenergie transportiert ?
2.
(ε1 , µ1)
x
(ε2 , µ2)
(ε3 , µ3)
d
z
Betrachten Sie drei kontinuierliche Medien, die durch
parallele ebene Grenzflächen im Abstand d getrennt sind
(siehe Skizze). Das mittlere Medium ist ein Leiter (ε2 =
i ωσ , µ2 = 1). Die angrenzenden Medien sind Isolatoren
(ε1 , µ1 ),(ε3 , µ3 ). Eine monochromatische ebene elektromagnetische Welle trifft senkrecht einfallend auf das leitende Medium.
(a) Bestimmen Sie die monochromatische ebene Welle in allen drei kontinuierlichen Medien.
(b) Bestimmen Sie die zeitlich gemittelten Poyntingschen Vektorfelder, die zum im ersten Medium reflektierten und im dritten Medium transmittierten Anteil gehören. Gibt es eine Schichtdichte d des zweiten Mediums, für die der reflektierte Anteil im ersten Medium verschwindet ?
(Aufgabe 3 siehe Rückseite)
Galilei-invariante modifizierte Elektrodynamik:
3. Betrachten Sie die modifizierten Maxwellschen Gleichungen
~ · E)(~
~ x, t) = ρ(~x, t)/ε0
(∇
~ · B)(~
~ x, t) = 0
(∇
~ × E)(~
~ x, t) = 0
(∇
~
~ × B)(~
~ x, t) = ∂ E (~x, t) + 1 ~j(~x, t),
c 2 (∇
∂t
ε0
(1)
(2)
(3)
(4)
die das Faradaysche Induktionsgesetz verletzen.
~ x, t)) zur Beschreibung des elek(a) Führen Sie elektromagnetische Potentialfelder (Φ(~x, t), A(~
tromagnetischen Feldes ein. Sind diese Potentialfelder eindeutig bestimmt ? Wie lauten die
Maxwellschen Gleichungen für diese Potentialfelder ? Gilt Ladungserhaltung ?
(b) Betrachten Sie eine spezielle Galilei-Transformation (t′ , ~x′ ) = (t, ~x + ~v t) und nehmen Sie
~ x, t)) und (ρ(~x, t), ~j(~x, t)) wie die Kompoan, dass sich die Komponenten von (Φ(~x, t), A(~
nenten von (t, ~x) transformieren. Zeigen Sie, dass auch im speziell Galilei-transformierten
Inertialsystem diesselben modifizierten Maxwellschen Gleichungen gelten. Wie ist dabei das
~ x, t), B(~
~ x, t) zu transformieren ?
elektromagnetische Feld (E(~