Skript-Teil 3

Kapitel 3
Fehleranalyse
Der Gauß-Algorithmus berechnet theoretisch die Lösung von Ax = b exakt. Wir hatten
u.a. an dem Beispiel mit der Hilbert-Matrix schon gesehen, daß dies in der Praxis nicht
stimmt, wenn der Algorithmus auf einem Rechner implementiert wurde.
Beispiel 3.1 Durch
p(x) = x7 − 7x6 + 21x5 − 35x4 + 35x3 − 21x2 + 7x − 1
ist ein Polynom 7ten Grads gegeben. Läßt man dieses Polynom von MATLAB im Intervall
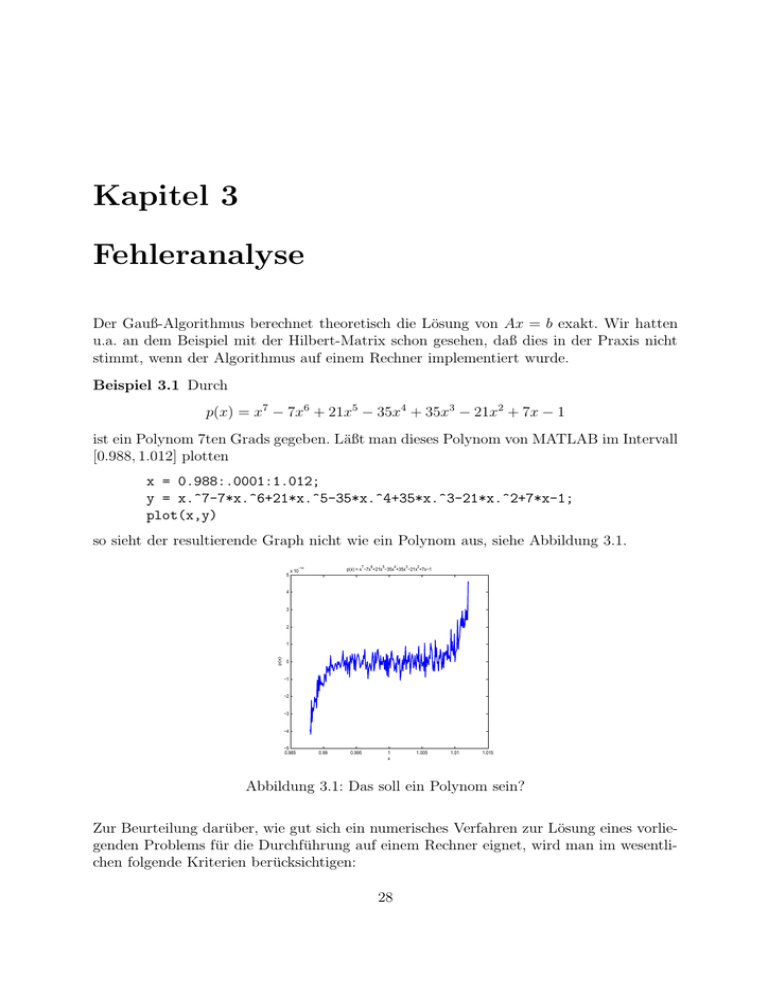
[0.988, 1.012] plotten
x = 0.988:.0001:1.012;
y = x.^7-7*x.^6+21*x.^5-35*x.^4+35*x.^3-21*x.^2+7*x-1;
plot(x,y)
so sieht der resultierende Graph nicht wie ein Polynom aus, siehe Abbildung 3.1.
p(x) = x7−7x6+21x5−35x4+35x3−21x2+7x−1
−14
5
x 10
4
3
2
p(x)
1
0
−1
−2
−3
−4
−5
0.985
0.99
0.995
1
x
1.005
1.01
1.015
Abbildung 3.1: Das soll ein Polynom sein?
Zur Beurteilung darüber, wie gut sich ein numerisches Verfahren zur Lösung eines vorliegenden Problems für die Durchführung auf einem Rechner eignet, wird man im wesentlichen folgende Kriterien berücksichtigen:
28
29
1. Genauigkeit des Ergebnisses, Verläßlichkeit
2. Rechenzeitbedarf, Speicherbedarf.
Die Bewertung der Eigenschaften 2. hängt stark von der äußeren Konfiguration des zur
Verfügung stehenden Rechners ab. Die Beurteilung eines Verfahrens oder der Vergleich
zweier Verfahren inbezug auf Rechenzeit- und Speicherbedarf ist i.a. gut durchführbar.
Die meisten numerischen Verfahren arbeiten nur richtig, falls die gegebenen Daten des
Problems gewissen Bedingungen genügen. Bei den speziell vorliegenden Daten eines Problems ist häufig nicht ersichtlich oder leicht überprüfbar, ob die für das betrachtete Verfahren notwendigen Voraussetzungen erfüllt sind. Dies gilt insbesondere, wenn es sich
hierbei um ein während der Rechnung zu erzeugendes Zwischenergebnis in einem komplexeren Verfahren handelt. Die Verläßlichkeit eines Verfahrens beurteilt man danach, wie
ein solches Versagen des Verfahrens den Rechenprozeß beeinflußt, z.B. durch Abbruch,
Meldung oder Korrektur. Insbesondere sollte es nicht möglich sein, daß aufgrund eines
Versagens des Verfahrens oder von Teilen des Verfahrens ein sinnvoll erscheinendes, aber
völlig falsches Ergebnis produziert wird.
Um Aussagen über die Genauigkeit des Ergebnisses zu erhalten, ist eine detaillierte Betrachtung des numerischen Verfahrens bezüglich aller möglichen auftretenden Fehler und
ihrer Einflüsse auf das Ergebnis erforderlich. In diesem Zusammenhang versteht man
unter Fehler jeweils die Abweichung eines nach bestimmten Vorschriften produzierten
Ergebnisses vom gewünschten Resultat, also zum Beispiel nicht einen Programmfehler.
Man unterscheidet hier drei wesentliche Fehlerarten: 1. Meßfehler, 2. Verfahrensfehler, 3.
Rundungsfehler.
1. Meßfehler: Bei der Gewinnung eines mathematischen Problems aus einem Anwenderproblem werden fast stets eine Reihe idealisierender Annahmen gemacht, etwa
indem Größen von geringem Einfluß vernachlässigt und funktionale Zusammenhänge
stark vereinfacht werden. Schon aus diesem Grund wird die Lösung des mathematischen Problems von der Lösung des Ausgangsproblems aus der Anwendung abweichen. Zudem erhält man die Daten des mathematischen Problems, zum Beispiel
die Elemente einer Matrix, deren Eigenwerte gesucht sind, häufig als Ergebnisse von
Messungen, die nur mit beschränkter Genauigkeit durchgeführt werden können, oder
als bereits mit Fehlern behaftete Ergebnisse anderer Berechnungen.
2. Verfahrensfehler: Für einige mathematische Probleme gibt es numerische Verfahren, die nach einer gewissen Anzahl von Berechnungsschritten (bei exakter Rechnung) die gesuchte Lösung ermittelt haben. Das Gaußsche Eliminationsverfahren
zur Lösung von linearen Gleichungssystemen ist zum Beispiel ein solches Verfahren.
Für die meisten Aufgaben muß man jedoch iterative Verfahren verwenden, mit denen man schrittweise eine Folge von Näherungslösungen bestimmen kann, die gegen
die gesuchte Lösung konvergiert. Dazu gehören zum Beispiel bis auf sehr spezielle
Fälle alle Eigenwertbestimmungen von Matrizen, da die Eigenwerte als Nullstellen
des charakteristischen Polynoms im allgemeinen nicht mit endlich vielen rationalen
Operationen berechenbar sind. Bei solchen Verfahren bricht man, abhängig von geeigneten Kriterien, die Berechnung nach einer gewissen Anzahl von Schritten mit
30
KAPITEL 3. FEHLERANALYSE
einer Näherungslösung ỹ ab. Die Abweichung y − ỹ dieser Näherungslösung von der
gesuchten Lösung y des Problems nennt man Verfahrensfehler oder auch Abbrechfehler.
3. Rundungsfehler: Die Rundungsfehlerproblematik wird in den folgenden Abschnitten
ausführlich behandelt.
3.1
Zahldarstellung
Ein Teil der Problematik liegt in der Art und Weise wie reelle (und komplexe) Zahlen in
einem Computer dargestellt werden. Z.B. hat π bekanntermaßen unendlich viele Nachkommastellen. Der Arbeitsspeicher eines Computer ist jedoch beschränkt, so daß nur endlich
viele Nachkommastellen gespeichert werden können. Es gibt verschiedene Darstellungen,
die zur Speicherung von reellen Zahlen verwendet werden können. Sie basieren auf dem
folgenden Satz; einen Beweis finden Sie z.B. in O. Forster, Analysis I, Vieweg-Verlag.
Satz 3.2 (b-adische Entwicklung) Für x ∈ R, b ∈ N\{1} existieren eindeutig bestimmte j ∈ {0, 1}, ` ∈ Z und für alle k ∈ Z mit k ≤ ` eindeutige γk ∈ {0, . . . , b − 1}, so daß
x = (−1)j
X̀
γ k bk ,
(3.1)
k=−∞
wobei γ` 6= 0 für x 6= 0, j = ` = 0 für x = 0, und γk < b − 1 für unendlich viele k ≤ `.
Falls die Basis b festgelegt ist, kann man die b-adische Entwicklung auch durch Aneinanderreihung der Ziffern γk angeben:
(x)b := ±γ` γ`−1 . . . γ0 .γ−1 γ−2 . . . .
Im täglichen Leben wird meist im Dezimalsystem gerechnet, d.h. b = 10 und
x=±
X̀
k=−∞
γk · 10k = ±γ` γ`−1 . . . γ0 .γ−1 γ−2 . . . = (x)10
mit Ziffern γk ∈ {0, 1, . . . , 9}.
Beispiel 3.3 Für die Zahl x = 123.456 erhalten wir ` = 2 und
γ2 = 1, γ1 = 2, γ0 = 3, γ−1 = 4, γ−2 = 5, γ−3 = 6, γk = 0 für k ≤ −4.
Die meisten Computer stellen Zahlen zur Basis b = 2 dar.
Beispiel 3.4 Die Dezimalzahl 1123 kann wie folgt ins Binärsystem (d.h. b = 2) umgerechnet werden
1123 =
=
=
=
=
1024 + 99
210 + 64 + 35
210 + 26 + 32 + 3
210 + 26 + 25 + 2 + 1
210 + 26 + 25 + 21 + 20 ,
31
3.1. ZAHLDARSTELLUNG
also
(1123)2 = 10001100011.
Es ist ` = 10, γ10 = γ6 = γ5 = γ1 = γ0 = 1, alle anderen γk sind Null.
Leider lassen sich nicht alle reellen Zahlen mit endlich vielen Nachkommastellen auch im
Binärsystem mit endlich vielen Ziffern darstellen.
Beispiel 3.5 Die reelle Zahl 0.1 hat die 2-adische Darstellung
(0.1)2 = 0.00011001100110011....
Die Zahlenfolge 0011 wiederholt sich unendlich oft.
Die Darstellung (3.1) ist äquivalent zu
x =
(
(−1)j
X̀
k=−∞
= (−1)j
∞
X
γ`−i+1
bi
i=1
= (−1)j
Da γ` = α1 6= 0 folgt sofort
1
b
γk bk−`−1
∞
X
αi
i=1
{z
|
:=m
≤ |m| < 1.
bi
)
· b`+1
b`+1
be .
(3.2)
}
Definition 3.6 Die Darstellung (3.2) für x ∈ R heißt normalisierte Gleitpunktdarstellung von x bzgl. der Basis b. Dabei heißt
m = (−1)
j
∞
X
αi
i=1
,
j ∈ {0, 1}, αi ∈ {0, 1, . . . , b − 1}
βi b i ,
p ∈ {0, 1}, βi ∈ {0, 1, . . . , b − 1}
bi
die Mantisse und
e =: (−1)
p
∞
X
i=0
der Exponent von x bzgl b. Die Gleitpunktdarstellung heißt normalisiert, da α 1 6= 0.
Beispiel 3.7 Für b = 10 ist die normalisierte Gleitpunktdarstellung von x = 35657.23
gegeben durch
3
5
6
5
7
2
3
5
0.3565723 · 10 =
+
+
+
+
+
+
· 105 .
101 102 103 104 105 106 107
32
KAPITEL 3. FEHLERANALYSE
Auf einem Rechner stehen zur Speicherung nur endlich viele Speicherplätze (Ziffern) zur
Verfügung. Daher wird die Mantisse einer normalisierten Gleitpunktzahl im Rechner auf
t Ziffern und der Exponent auf s Stellen beschränkt.
Definition 3.8 Für b ∈ N\{1}, t, s ∈ N ist die Menge der normalisierten Gleitpunktzahlen der Mantissenlänge t und Exponentenlänge s zur Basis b durch
M(b, t, s) =
(
(−1)j
t
X
αi
i=1
bi
· b(−1)
Ps
p
i=0 ,βi b
i
)
α , β ∈ {0, 1, . . . , b − 1},
i i
∪ {0}
α1 6= 0, j, p ∈ {0, 1}
gegeben. Schematisch lassen sich diese Zahlen wie folgt darstellen
±α1 α2 . . . αt | ± β0 β1 β2 . . . βs .
x ∈ M(b, t, s) heißen Computerzahlen oder Maschinenzahlen.
Hiermit sind 2(b − 1)bt−1 (2bs+1 − 1) + 1 Zahlen darstellbar. Zudem lassen sich stets die
kleinste darstellbare Zahl xmin und die größte darstellbare Zahl xmax leicht angeben.
Beispiel 3.9 Am Beispiel b = 2, t = 3, s = 1 soll die Darstellung verdeutlicht werden.
Schematisch läßt sich hier jede Zahl mittels
± α 1 α 2 α 3 | ± β 0 β1
darstellen, d.h.
±(α1 2−1 + α2 2−2 + α3 2−3 ) · 2±(β0 2
Die verfügbaren Mantissen sind
Basis 2
Basis 10
±100
=
ˆ ±1/2
±101
=
ˆ ±5/8
±110
=
ˆ ±3/4
±111
=
ˆ ±7/8
Die verfügbaren Exponenten sind
±00
±10
±01
±11
=
ˆ
=
ˆ
=
ˆ
=
ˆ
0
±1
±2
±3
0 +β
12
1)
33
3.2. RUNDUNGSFEHLER
Die darstellbaren Zahlen sind daher
±000| ± 00
±100| ± 00
±100| + 10
±100| − 10
±100| + 01
±100| − 01
±100| + 11
±100| − 11
±101| ± 00
±101| + 10
±101| − 10
..
.
=
ˆ
=
ˆ
=
ˆ
=
ˆ
=
ˆ
=
ˆ
=
ˆ
=
ˆ
=
ˆ
=
ˆ
=
ˆ
0
± 12
± 21
± 21
± 21
± 21
± 21
± 21
± 85
± 85
± 85
· 20 = ± 12
· 21 = ±1
· 2−1 = ± 14
· 22 = ±2
· 2−2 = ± 18
· 23 = ±4
1
· 2−3 = ± 16
5
0
· 2 = ±8
· 21 = ± 54
5
· 2−1 = ± 16
±111| + 11 =
ˆ ± 87 · 23 = ±7
7
±111| − 11 =
ˆ ± 87 · 2−3 = ± 64
Es sind also insgesamt 57 Zahlen darstellbar, die kleinste darstellbare positive Zahl ist
1
· 2−3 = 2−4 , die größte darstellbare positive Zahl ist 78 · 23 = 7. In der Nähe von 0 liegen
2
die Zahlen am dichtesten. Die Zahl 0.1 z.B. ist hier nicht exakt darstellbar. Denn
1
0.8
0.6
0.4
0.2
0
−0.2
−0.4
−0.6
−0.8
−1
0
1
2
3
4
5
6
7
Abbildung 3.2: die nichtnegativen Maschinenzahlen für b = 2, t = 3, s = 1
0.1=
ˆ + 000110011001100 . . . | + 00
und damit wird 0.1 dargestellt als
was der Dezimalzahl
3.2
3
32
+110| − 11
= 0.09375 entspricht.
Rundungsfehler
Um reelle Zahlen im Computer zu speichern, muß man sie als Maschinenzahl darstellen.
Dazu wird jede Zahl zunächst als normalisierte Gleitpunktzahl zur vom Rechner verwendeten Basis b dargestellt. Da die Mantisse einer Maschinenzahl nur t Stellen besitzt,
werden alle weiteren Stellen der Mantisse der zu speichernden Zahl abgeschnitten, bzw.
es muß auf t Stellen gerundet werden. Es entstehen Rundungsfehler.
34
KAPITEL 3. FEHLERANALYSE
Beispiel 3.10 Angenommen, der Computer stellt reelle Zahlen in M(10, 5, 1) dar. Dann
wird x = 2.5684 dargestellt als
0.25684 · 101 ,
die Zahl kann also exakt dargestellt werden. Die Zahl z = 3.4579103 wird als
0.34579 · 101
dargestellt. Die Nachkommastellen 0.0000103 gehen verloren.
Allgemein gilt: Jedes reelle x wird im Rechner als x ∈ M(b, t, s) dargestellt mit f l(x) =
x(1 + ε). Genauer gilt für
P
−i e
x
= ±( ∞
i=1 αi b )b mit α1 6= 0 und x ∈ [xmin , xmax ]
f l(x) =
P
±( ti=1 αi b−i )be
für αt+1 < b/2
Pt
−i
−t e
±( i=1 αi b + b )b für αt+1 ≥ b/2
Für |x| < xmin spricht man von ’underflow’. x wird häufig als f l(x) = 0 dargestellt. Bei
|x| > xmax spricht man von ’overflow’, x liegt außerhalb des darstellbaren Bereichs, ein
solches x wird häufig mittels Inf dargestellt.
Lemma 3.11 Für den absoluten Fehler in der Zahldarstellung gilt
1
|f l(x) − x| ≤ b−t be ,
2
für den relativen Fehler
b
f l(x) − x
| < b−t .
|
x
2
1 1−t
Definition 3.12 Die Größe 2 b := u bezeichnet man als relative Maschinengenauigkeit
(’unit roundoff ’).
Die relative Maschinengenauigkeit gibt also an, welche relativen Fehler beim Runden
maximal entstehen können.
Bemerkung 3.13 Um Aussagen über die Genauigkeit approximativer Größen zu treffen, muß man den relativen Fehler abschätzen, der absolute Fehler gibt darüber keine
ausreichende Auskunft!
Dazu betrachte man die Zahlen x = 25.317 und x
e = 25.313. x
e stimmt also auf 4 Stellen
mit x überein. Der relative Fehler beträgt
|x − x
e|
0.004
=
≈ 0.16 · 10−3 .
|x|
25.317
Wie man sich leicht überlegt, entspricht die Anzahl der korrekten Dezimalstellen dem
negativen Exponenten des relativen Fehlers plus/minus 1.
Betrachtet man y = 0.001 und ye = 0.002, so besitzt ye keine korrekte Stelle. Der absolute
Fehler |y − ye| = 10−3 ist klein und deutet bei fehlerhafter Interpretation eine Genauigkeit
von 2 bis 3 Stellen an. Der relative Fehler
|y − ye|
=1
|y|
hingegen signalisiert eindeutig, daß ye keine korrekte Stelle besitzt.
35
3.3. GLEITPUNKTOPERATIONEN
3.3
Gleitpunktoperationen
Da R ein Körper ist, ergibt die Summe zweier reeller Zahlen wieder eine reelle Zahl. Wie
das folgende Beispiel zeigt, gilt dies für die Summe zweier Zahlen aus M(b, t, s) nicht
notwendigerweise.
Beispiel 3.14 Wir betrachten M(10, 5, 1) und die reellen Zahlen
x = 2.5684
y = 0.0032791
z = 3.4579103
Diese werden als
f l(x) = 0.25684 · 101
(= x)
−2
f l(y) = 0.32791 · 10
(= y)
f l(z) = 0.34579 · 101 (6= z)
dargestellt. Die Ergebnisse der elementaren Rechenoperationen
f l(x) + f l(y)
f l(x) − f l(z)
f l(x) · f l(y)
f l(y)/f l(z)
=
=
=
=
2.5716791
−0.8895
0.00842204044
0.0009482923161456376...
sind nicht alle wieder Maschinenzahlen. Die Ergebnisse müssen erst zu Maschinenzahlen
gerundet werden.
f l(f l(x) + f l(y))
f l(f l(x) − f l(z))
f l(f l(x) · f l(y))
f l(f l(y)/f l(z))
=
=
=
=
0.25717 · 101
−0.8895 · 100
0.84220 · 10−2
0.94829 · 10−3
Aufgrund dieser Rundungsfehlerproblematik besitzen Computer nur eine Pseudoarithmetik, die das Ergebnis einer Gleitpunktoperation beschreibt.
Definition 3.15 Die Gleitpunktoperationen
⊕, , ⊗, sind durch die üblichen Definitionen festgelegt, mit anschließendem Runden des Ergebnisses, damit wieder ein Wert aus M(b, t, s) entsteht. D.h., für alle x, y ∈ M(b, t, s) gilt
x⊕y
xy
x⊗y
xy
=
=
=
=
(x + y)(1 + ε), |ε| < u
(x − y)(1 + ε), |ε| < u
(x · y)(1 + ε), |ε| < u
(x y)(1 + ε), |ε| < u.
Die Operationen sind nicht definiert, wenn das Ergebnis außerhalb des durch M(B, p, q)
überdeckten Bereichs liegt.
36
KAPITEL 3. FEHLERANALYSE
Dieses Modell der Gleitpunktarithmetik gilt nur für Maschinenzahlen. Bei der Addition
zweier Zahlen x, y ∈ R ergeben sich also bereits drei Fehler: je einer beim Runden von x
und y zu einer Maschinenzahl
f l(x) = x(1 + εx ),
f l(y) = y(1 + εy ),
|εx | < u
|εy | < u,
sowie ein weiterer bei der Gleitpunktaddition
f l(x) ⊕ f l(y) = ( f l(x) + f l(y) )(1 + εx+y ), |εx+y | < u
= ( x(1 + εx ) + y(1 + εy ) )(1 + εx+y )
= ( (x + y) + (xεx + yεy ) )(1 + εx+y ).
Daraus folgt,
wenn x und y dasselbe Vorzeichen besitzen, d.h. sign(x) = sign(y), wobei
+1, falls a > 0
sign(a) =
:
−1, falls a < 0
|f l(x) ⊕ f l(y) − (x + y)|
=
≤
|(x + y)εx+y + (xεx + yεy )(1 + εx+y )
|x + y|u + (|x|u + |y|u)(1 + u)
=
=
|x + y|u + |x + y|u(1 + u)
|x + y|(2u + u2 ).
sign(x)=sign(y)
Der relative Fehler ist (bis auf den vernachlässigbar kleinen Term u2 ) maximal doppelt
so groß wie der relative Fehler der Summanden. Entsprechend können viele Additionen
zu einem großen akkumulierten Fehler führen.
Eine ähnliche Analyse zeigt, daß die Subtraktion zweier fast gleicher Zahlen zu einem sehr
großen relativen Fehler führen kann: Für x = y + µu folgt
2
|f l(x) f l(y) − (x − y)|
≤
|y| + Terme höherer Ordnung in u.
|x − y|
|µ|
D.h. der relative Rundungsfehler kann bei fast gleichen Operanden bis zum doppelten
Wert der Operanden anwachsen. Vorsicht ist also geboten, wenn Differenzen fast gleichgroßer Zahlen auftreten, da die Stellenauslöschung zu sehr großen Rundungsfehlern führt.
Zur Vermeidung von Auslöschung versucht man, den zu berechnenden Ausdruck so umzuformen, daß die Subtraktion zweier nahezu gleicher Zahlen vermieden wird.
Beispiel 3.16 Als Beispiel sei hier die Summation von Potenzreihen, deren Glieder alternierende Vorzeichen haben, genauer betrachtet.
Zur Berechnung von ex wird von der Reihenentwicklung
x2 x3
+
+...
e =1+x+
2!
3!
x
37
3.3. GLEITPUNKTOPERATIONEN
ausgegangen, nach der in M(10, 5, q) e−5,5 berechnet werden soll, also
e−5,5 =
1.000
−
5.500
+
15.125
−
27.730
+
38.129
−
41.942
+
38.446
−
30.208
...
+ 0.0026363
Bei einer Rechengenauigkeit von 5 Dezimalstellen ist bereits die 4. Stelle nach dem Dezimalpunkt, also die zweite Stelle im Ergebnis, unsicher. Dem überlagert sich die Fortpflanzung der Rundungsfehler bei den Gleitpunktoperationen, was hier das Ergebnis völlig
unbrauchbar macht. Der exakte Wert lautet auf 5 Stellen genau:
e−5,5 = 0.0040868.
Die Stellenauslöschung wäre vermieden worden, wenn man statt e−5,5 direkt e5,5 nach der
Reihenentwicklung ermittelt und dann den Kehrwert gebildet hätte:
1/(1 + 5.5 + 15.125 + . . .) = 0.0040865.
Neben der fatalen Auswirkung bei der Differenz fast gleicher Zahlen ergeben sich kritische
Situationen, wenn bei der Programmierung nicht berücksichtigt wird, daß für Gleitpunktaddition und -multiplikation weder das Assoziativ- noch das Distributivgesetz gilt:
Sei u, v, w ∈ M(b, t, s), dann ist im allgemeinen
(u ⊕ v) ⊕ w =
6
u ⊕ (v ⊕ w)
(u ⊗ v) ⊗ w =
6
u ⊗ (v ⊗ w)
u ⊗ (v ⊕ w) =
6
(u ⊗ v) ⊕ (u ⊗ w).
Beispiel 3.17 Betrachte M(10, 5, 1): Dann gilt

a = f l(a) = 0.98765

b = f l(b) = 0.012424
a + b + c = 0.9935308

c = f l(c) = −0.0065432
aber
(a ⊕ b)
(b ⊕ c)
(a ⊕ b) ⊕ c
a ⊕ (b ⊕ c)
=
=
=
=
f l(1.000074)
f l(0.0058808)
f l(0.9935568)
f l(0.9935308)
=
=
=
=
1.0001
0.0058808
0.9936
0.99353
D.h. a ⊕ (b ⊕ c) liefert das richtige Ergebnis, nicht aber (a ⊕ b) ⊕ c.