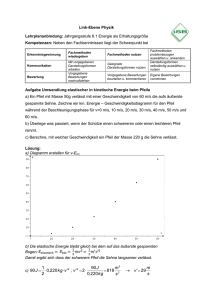
Ü 1.20: HERA: rel. Geschwindigkeit
Werbung

Link-Ebene Physik Lehrplananbindung: 11.3 Einblick in die Relativitätstheorie, Jgst. 11 Kompetenzen: Neben den Fachkenntnissen liegt der Schwerpunkt bei Erkenntnisgewinnung Kommunikation Bewertung Fachmethoden wiedergeben Mit vorgegebenen Darstellungsformen arbeiten Vorgegebene Bewertungen nachvollziehen Fachmethoden nutzen Geeignete Darstellungsformen nutzen Vorgegebene Bewertungen beurteilen und kommentieren Fachmethoden problembezogen auswählen u. anwenden Darstellungsformen selbständig auswählen u. nutzen Eigene Bewertungen vornehmen Ringbeschleuniger HERA Im Ringbeschleuniger HERA (Hadron-Elektron-Ring-Anlage) werden Protonen beschleunigt, bis sie eine kinetische Energie von ca. 900 GeV besitzen. a) Berechnen Sie die Geschwindigkeit dieser Elektronen mit der bekannten Formel m Ekin = v 2 . Nehmen Sie Stellung zu ihrem Ergebnis. Wie lässt sich der vermeintliche 2 Widerspruch auflösen? b) Berechnen Sie die Masse, die ein Elektron mit oben genannter Energie besitzt. c) Ermitteln Sie die tatsächliche Geschwindigkeit dieser Elektronen. Lösung: a) Klassisch: E kin = 1 mv 2 v = 2 2E kin m = 1,3 ⋅ 10 10 >c m s Die Geschwindigkeit wäre größer als die Lichtgeschwindigkeit. Dies kann nicht sein. Das Proton bewegt sich mit so großer Geschwindigkeit, dass eine relativistische Rechnung notwendig wird. Mit einer großen Geschwindigkeit geht eine Erhöhung der Masse des Protons einher, was wiederum Auswirkungen auf seine kin. Energie hat. Dies wird in der klassischen Mechanik nicht berücksichtigt. b) E ges = mc 2 = E kin + E 0 = 900,9GeV → m = 1,6 ⋅ 10 −24 kg ≈ 960m 0 c) m= m0 1− v2 c2 v = 9,9999995 c