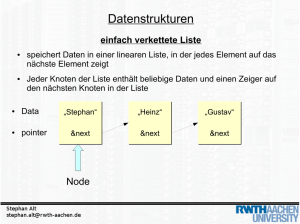
Lektion 5: Bäume Konzept Baum
Werbung
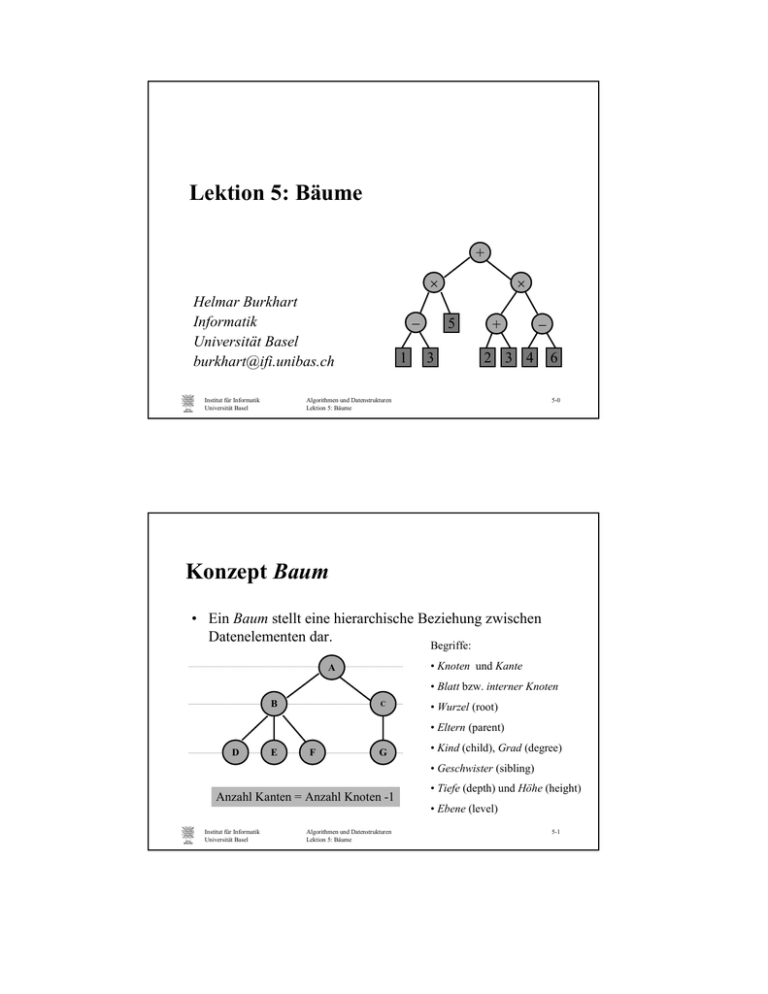
Lektion 5: Bäume + × Helmar Burkhart Informatik Universität Basel [email protected] Institut für Informatik Universität Basel − 1 × 5 3 + − 2 3 4 Algorithmen und Datenstrukturen Lektion 5: Bäume 6 5-0 Konzept Baum • Ein Baum stellt eine hierarchische Beziehung zwischen Datenelementen dar. Begriffe: • Knoten und Kante A • Blatt bzw. interner Knoten B C • Wurzel (root) • Eltern (parent) D E F G • Kind (child), Grad (degree) • Geschwister (sibling) Anzahl Kanten = Anzahl Knoten -1 • Tiefe (depth) und Höhe (height) • Ebene (level) Institut für Informatik Universität Basel Algorithmen und Datenstrukturen Lektion 5: Bäume 5-1 Bäume in der Bibliothek JDSL http://www.cs.brown.edu/cgc/jdsl Container EulerTour PositionalContainer InOrderIterator InspectableTree Tree InspectableBinaryTree BinaryTree NodeBinaryTree Institut für Informatik Universität Basel Algorithmen und Datenstrukturen Lektion 5: Bäume 5-2 ADT Nichtveränderbarer Baum (1) Es werden zu einem gegebenen Knoten eines Baums Nachbarschaftsrelationen und Eigenschaften zugreifbar gemacht. interface InspectableTree • boolean isExternal(Position node) • boolean isInternal(Position node) • boolean isRoot(Position node) • Position firstChild(Position node) • Position lastChild(Position node) • Position childAtRank(Position node, int rank) Institut für Informatik Universität Basel Algorithmen und Datenstrukturen Lektion 5: Bäume 5-3 ADT Nichtveränderbarer Baum (2) • • • • int PositionIterator int Position rankOfChild(Position child) children(Position node) numChildren(Position node) parent(Position node) • • • • Position Position Position PositionIterator root() siblingBefore(Position node) siblingAfter(Position node) siblings(Position node) Institut für Informatik Universität Basel Algorithmen und Datenstrukturen Lektion 5: Bäume 5-4 ADT Veränderbarer Baum (1) Die Schnittstelle Tree stellt Operationen zur Veränderung eines Baums bereit. interface Tree extends InspectableTree • Position insertChildAtRank(Position node, int rank, Object elem) • Position insertFirstChild(Position node, • Position • Position • Position Institut für Informatik Universität Basel Object elem) insertLastChild(Position node,...) insertAfterSibling(Position node,...) insertBeforeSibling(Position node,...) Algorithmen und Datenstrukturen Lektion 5: Bäume 5-5 ADT Veränderbarer Baum (2) • Object • Tree • Position • Object • Object • Tree Institut für Informatik Universität Basel contract(Position node) cut(Position node) expand(Position fromChild, Position toChild, Object elem) link(Position extNode, Tree t) removeExternal(Position node) replaceSubtree(Position node, Tree t) Algorithmen und Datenstrukturen Lektion 5: Bäume 5-6 Konzept Binärer Baum Ein binärer Baum ist ein Baum bei dem alle internen Knoten den Grad 2 haben. Rekursive Definition: Ein binärer Baum ist entweder ein Blatt oder ein interner Knoten mit 2 Kindern, die selber binäre Bäume sind. Institut für Informatik Universität Basel Algorithmen und Datenstrukturen Lektion 5: Bäume 5-7 Eigenschaften binärer Bäume • Anzahl Blätter = Anzahl interne Knoten + 1. • Anzahl Knoten auf Ebene i ist kleiner oder gleich 2i • Anzahl der Blätter ist kleiner oder gleich 2h wobei h die Höhe des Baums ist. Institut für Informatik Universität Basel Algorithmen und Datenstrukturen Lektion 5: Bäume 5-8 ADT Nichtveränderbarer binärer Baum interface InspectableBinaryTree extends InspectableTree • Position leftChild(Position node) • Position rightChild(Position node) • Position sibling(Position node) Institut für Informatik Universität Basel Algorithmen und Datenstrukturen Lektion 5: Bäume 5-9 ADT Veränderbarer binärer Baum interface BinaryTree extends InspectableBinaryTree • BinaryTree cut(Position node) • void expandExternal(Position node) • void graftOnLeft(Position subtreeRoot, Object eltOfParent, BinaryTree newSubtree) • void graftOnRight(...) • Object link(Position node, BinaryTree newSubtree) • void removeAboveExternal(Position node) • BinaryTree replaceSubtree(Position subtreeRoot, BinaryTree newSubtree) Institut für Informatik Universität Basel Algorithmen und Datenstrukturen Lektion 5: Bäume 5-10 Beispiel Binärer Baum Ein Anwendung binärer Bäume ist die Speicherung arithmetischer Ausdrücke. + × × (1-3)× 5 + (2+3)×(4-6) − PostorderTraversieren liefert die Polnische Notation: Institut für Informatik Universität Basel 1 Algorithmen und Datenstrukturen Lektion 5: Bäume 5 3 − + 2 3 4 6 5-11 Binärer Baum mittels Folge Wir nummerieren die Knoten wie folgt: • Wurzel erhält Nummer 1. • Der Knoten k habe die Nummer p(k). Das linke Kind erhält Nummer 2 × p(k), das rechte 2 × p(k) +1 Nummer wird als Rang verwendet. Institut für Informatik Universität Basel Algorithmen und Datenstrukturen Lektion 5: Bäume 5-12 Binärer Baum mittels Verkettungen (1) class T_Node extends D-Node implements Position{ private T_Node parent; // Konstruktor public T_Node(Object e, T_Node p, T_Node l, T_Node r){ super(e,l,r); parent = p; } Institut für Informatik Universität Basel Algorithmen und Datenstrukturen Lektion 5: Bäume 5-13 Binärer Baum mittels Verkettungen (2) root Institut für Informatik Universität Basel Algorithmen und Datenstrukturen Lektion 5: Bäume 5-14 Traversieren von Bäume Es gibt verschiedene Strategien zum Besuchen der Knoten in einem Baum: • Breitensuche (breadth-first) • Tiefensuche (depth-first) – Präorder-Strategie: "Knoten am Anfang besuchen" – Postorder-Strategie: "Knoten am Schluss besuchen" – Inorder-Strategie: "Knoten zwischendurch besuchen" Institut für Informatik Universität Basel Algorithmen und Datenstrukturen Lektion 5: Bäume 5-15 Traversieren mit Präorder-Strategie Präorder-Strategie: "Knoten am Anfang besuchen" Algorithmus Präorder(Knoten k) "besuche" k forall c ∈ Kind(k) do Präorder(c) Anwendung: Hierarchisches Dokument (Buch) von Anfang bis Ende lesen. Institut für Informatik Universität Basel Algorithmen und Datenstrukturen Lektion 5: Bäume 5-16 Traversieren mit Postorder-Strategie Postorder-Strategie: "Knoten am Schluss besuchen" Algorithmus Postorder(Knoten k) forall c ∈ Kind(k) do Postorder(c) "besuche" k Anwendung: Speicherverbrauch in Unterverzeichnissen berechnen. Institut für Informatik Universität Basel Algorithmen und Datenstrukturen Lektion 5: Bäume 5-17 Traversieren mit Inorder-Strategie Inorder-Strategie: "Knoten zwischendurch besuchen" Algorithmus Inorder(Knoten k) nc ← Anzahl_Kinder(k) Inorder(1. Kind) for i ← 2 to nc do "Besuche" k Inorder(i. tes Kind) Institut für Informatik Universität Basel Anwendung: Arithmetische Berechnungen Algorithmen und Datenstrukturen Lektion 5: Bäume 5-18 Euler Tour Die Euler-Tour ist ein Rundgang durch den Baum, wobei jeder interne Knoten 3 Mal besucht wird: • von links kommend • von unten kommend • von rechts kommend Alle vorher genannten Traversierstrategien sind Spezialisierungen der Euler-Tour. Institut für Informatik Universität Basel Algorithmen und Datenstrukturen Lektion 5: Bäume 5-19 Klasse Euler Tour abstract class EulerTour • • • • • • void void void void void void execute(InspectableTree tree) init() visitBetweenChildren(Position pos) visitExternal(Position pos) visitFirstTime(Position pos) visitLastTime(Position pos) Institut für Informatik Universität Basel Algorithmen und Datenstrukturen Lektion 5: Bäume 5-20 Traversieren eines binären Baums void traverseNode(Position p){ if (tree.isExternal(p)) visitExternal(p) else{ visitFirstTime(p); traverseNode(tree.leftChild(p)); visitBetweenChildren(p); traverseNode(tree.rightChild(p)); visitLastTime(p); } Institut für Informatik Universität Basel Algorithmen und Datenstrukturen Lektion 5: Bäume 5-21