Pythagoras und Strahlensätze

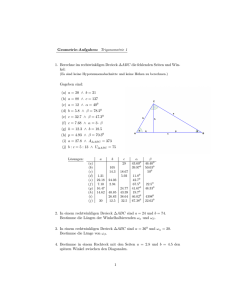
Name:
Seite: 1
Fachhochschule Nordwestschweiz (FHNW)
Pythagoras und Strahlensätze
Dozent: R. Burkhardt ([email protected])
Klasse: Semester: Datum: -
Büro: 4.613
1. Aufgabe
Bestimme y in Abhängigkeit von r.
y
3
r
2
r
2. Aufgabe
Bestimme in einem gleichschenkligen, rechtwinkligen Dreieck mit der Hypothenuse c = 10cm die Längen der
Seitenhalbierenden und den Radius des Inkreises.
3. Aufgabe
Von einem rechtwinkligen Dreieck ABC (Hypothenuse c), kennt man die Kathete b = 12m und die Seitenhalbierende sc = 6.5m. Bestimme alle Seiten und Winkel dieses Dreiecks.
4. Aufgabe
Bestimme in untenstehender Figur den Radius x des kleinen Kreises in Abhängigkeit des Seitenlänge a des
Quadrates.
5. Aufgabe
-
Pythagoras und Strahlensätze
-
Name:
Seite: 2
In der untenstehenden Skizze kennt man das Verhältnis der parallelen Abschnitte
AB
2x
2
=
=
CD
3x
3
und die Strecken AD = 20cm und BC = 15cm. Bestimme die Entfernung des Schnittpunkts S von den
Punkten A, B, C und D.
6. Aufgabe
Von einem rechtwinkligen Dreieck ABC, kennt man die Kathete a = 5cm und die Höhe hc = 3cm. Bestimme
alle Seiten und Winkel dieses Dreiecks.
7. Aufgabe
Gegeben sei das allgemeine Dreieck ABC mit den Seiten a = 9cm, b = 5cm und c = 11cm. Weiter sei
das Dreieck A3 B 3 C, welches durch Parallelverschiebung der Seite c entsteht, so dass der Umfang U 3 = 10cm
beträgt. Bestimme die Seitenlängen des Dreiecks A3 B 3 C und das Verhältnis der Flächeninhalte der beiden
Dreiecke.
C
A'
B'
B
A
8. Aufgabe
Eine Last F = 5kN ist an der nachfolgenden Aufhängung angebracht (AC = 2m, BC = 1m). Bestimme die
Kräfte in den beiden Stäben (die Kraft wirkt in Stabrichtung).
A
α
F
C
B
9. Aufgabe
Bestimme x in Abhängigkeit von r:
-
Pythagoras und Strahlensätze
-
Name:
Seite: 3
x
r
10. Aufgabe
Die Mittelpunkte zweier Kreise mit den Radien r1 und r2 besitzen die Entfernung d > r1 + r2 . Bestimme die
Länge ihrer gemeinsamen Tangenten.
11. Aufgabe
Gegeben sei ein rechtwinkliges Dreieck ABC (rechter Winkel bei C). Wenn man die Höhe vom Punkt C auf
die Seite c zieht, erhält man den Punkt D. Nun zieht man Parallelen zu den Seiten a und b durch den Punkt D
und erhält die Schnittpunkte E und F auf den Katheten. Bestimme den Flächeninhalt des Rechtecks CDEF
wenn
(a) a = 12 und b = 10
(b) allgemein aus a und b.
-
Pythagoras und Strahlensätze
-