Geometrie-Aufgaben: Trigonometrie 1 1. Berechne im

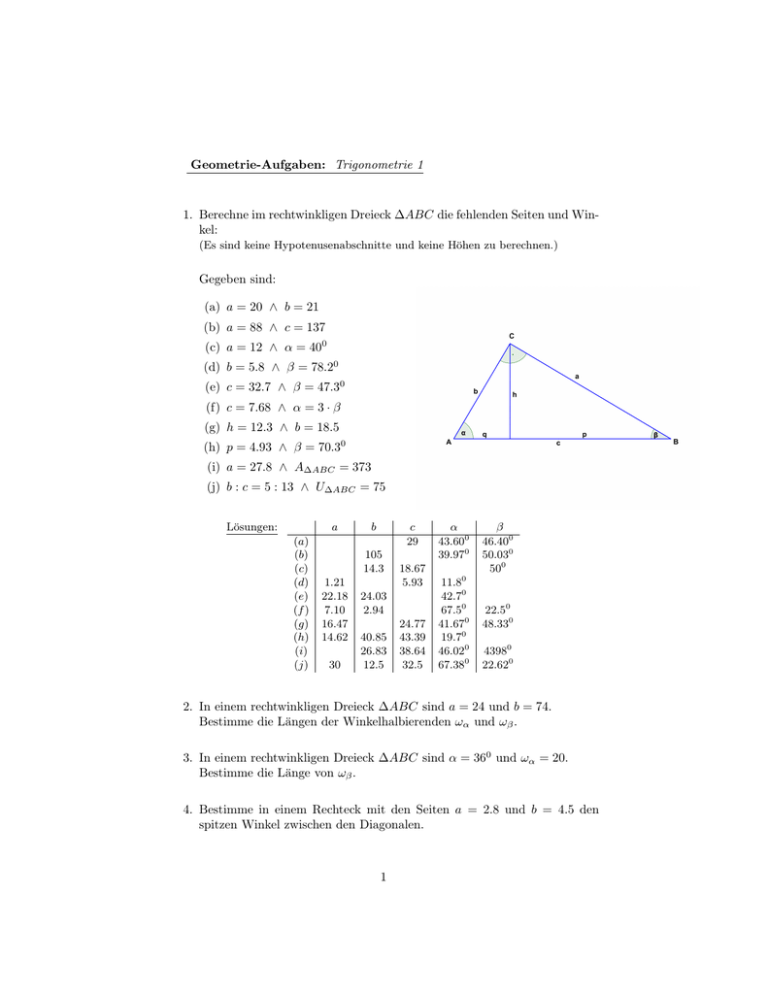
Geometrie-Aufgaben: Trigonometrie 1
1. Berechne im rechtwinkligen Dreieck ∆ABC die fehlenden Seiten und Winkel:
(Es sind keine Hypotenusenabschnitte und keine Höhen zu berechnen.)
Gegeben sind:
(a) a = 20 ∧ b = 21
(b) a = 88 ∧ c = 137
(c) a = 12 ∧ α = 400
(d) b = 5.8 ∧ β = 78.20
(e) c = 32.7 ∧ β = 47.30
(f) c = 7.68 ∧ α = 3 · β
(g) h = 12.3 ∧ b = 18.5
(h) p = 4.93 ∧ β = 70.30
(i) a = 27.8 ∧ A∆ABC = 373
(j) b : c = 5 : 13 ∧ U∆ABC = 75
Lösungen:
a
(a)
(b)
(c)
(d)
(e)
(f )
(g)
(h)
(i)
(j)
b
c
29
105
14.3
1.21
22.18
7.10
16.47
14.62
30
18.67
5.93
24.03
2.94
40.85
26.83
12.5
24.77
43.39
38.64
32.5
α
43.600
39.970
11.80
42.70
67.50
41.670
19.70
46.020
67.380
β
46.400
50.030
500
22.50
48.330
43980
22.620
2. In einem rechtwinkligen Dreieck ∆ABC sind a = 24 und b = 74.
Bestimme die Längen der Winkelhalbierenden ωα und ωβ .
3. In einem rechtwinkligen Dreieck ∆ABC sind α = 360 und ωα = 20.
Bestimme die Länge von ωβ .
4. Bestimme in einem Rechteck mit den Seiten a = 2.8 und b = 4.5 den
spitzen Winkel zwischen den Diagonalen.
1
5. Bestimme die Grösse der Innenwinkel eines Rhombus mit den Diagonalen
e = 57.2 und f = 81.7.
6. Wenn die Sonnenstrahlen 350 gegen die Waagrechte geneigt sind, wirft
eine Fichte einen 30m langen Schatten.
Bestimme die Länge der Fichte.
7. Unter welchem Neigungswinkel treffen die Sonnnenstrahlen auf dem Boden auf, wenn ein senkrechter Pfahl einen Schatten wirft, der
(a) doppelt so lang,
(b) halb so lang
wie der Pfahl selber ist?
8. Das obere Ende einer 5m langen Leiter erreicht an einer Hauswand angelehnt eine Höhe von 4.5m.
Bestimme den Neigungswinkel der Leiter.
9. Wenn das untere Ende der Leiter 2m von der Hauswand entfernt ist, bildet
die Leiter mit der Wand einen Winkel von 200 ,
(a) Bestimme die Länge der Leiter.
(b) Wie ändert sich der Winkel zwischen Leiter und Hauswand, wenn
das Ende der Leiter
i. 1.8m
ii. 2.2m
iii. 2.5m
von der Wand entfernt ist.
(c) Stelle den Zusammenghang aus Aufgabe (b) graphisch dar.
10. Ein gleichschenkliges Dreieck ∆ABC hat einen spitzen Winkel von 300
und einen Umfang von 30.
Bestimme die Länge der Basis und den Flächeninhalt des Dreiecks ∆ABC
11. In einem Kreis mit Radius r = 8 misst der zu einer Sehne gehörende Mittelpunktswinkel 1440 .
Bestimme die Sehnenlänge und den Flächeninhalt des dazugehörigen Kreissegments.
2