Dreieckslehre

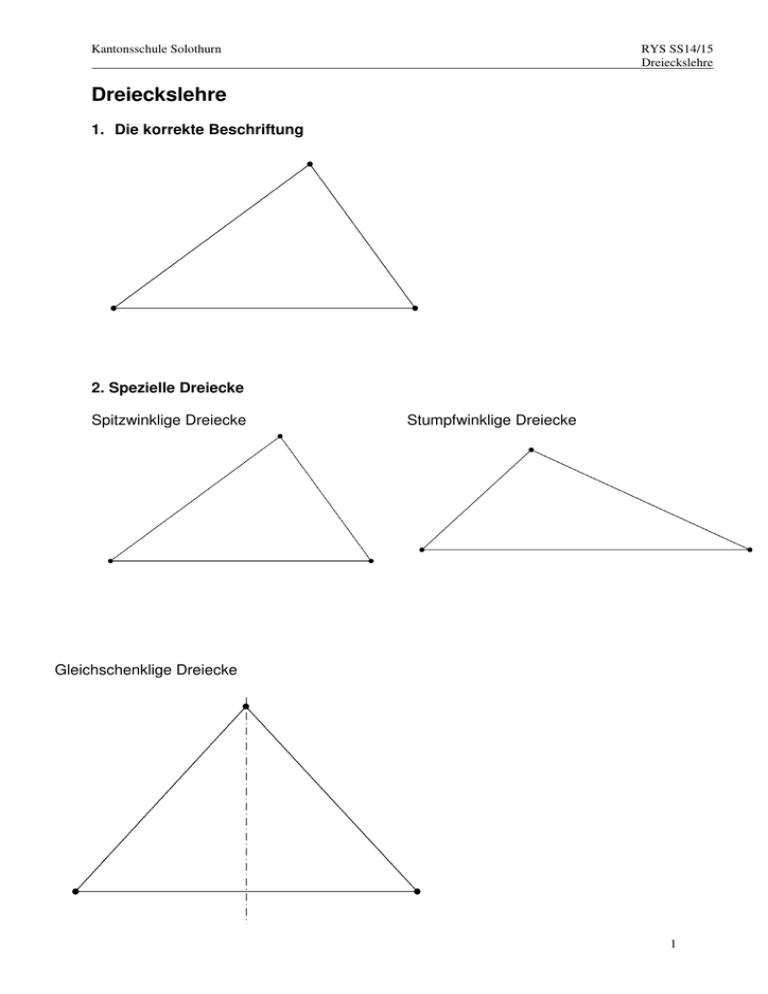
Kantonsschule Solothurn
RYS SS14/15
Dreieckslehre
Dreieckslehre
1. Die korrekte Beschriftung
2. Spezielle Dreiecke
Spitzwinklige Dreiecke
Stumpfwinklige Dreiecke
Gleichschenklige Dreiecke
1
Gleichseitige Dreiecke
Rechtwinklige Dreiecke (Thaleskreis)
2
Kantonsschule Solothurn
RYS SS14/15
Dreieckslehre
3. Spezielle Linien im Dreieck
a) Die Mittelsenkrechten im Dreieck
b) Die Winkelhalbierenden im Dreieck
3
c) Die Seitenhalbierenden im Dreieck
d) Die Höhen im Dreieck
4
Kantonsschule Solothurn
RYS SS14/15
Dreieckslehre
4. Kongruenzsätze im Dreieck
1. Kongruenzsatz: Zwei Dreiecke sind kongruent zueinander, wenn sie in den Längen aller
entsprechenden Seiten übereinstimmen [sss].
2. Kongruenzsatz: Zwei Dreiecke sind kongruent zueinander, wenn sie in den Längen
zweier Seiten und der Grösse des von diesen Seiten eingeschlos-senen Winkels
übereinstimmen [sws]
3. Kongruenzsatz: Zwei Dreiecke sind kongruent zueinander, wenn sie in den Längen
zweier ihrer Seiten und dem der längeren Seite gegenüberliegenden Winkel
übereinstimmen [ssw]
4. Kongruenzsatz: Zwei Dreiecke sind kongruent zueinander, wenn sie in der Länge einer
ihrer Seiten und in den Grössen zweier Winkel übereinstimmen [wsw und sww]
Zusammenfassend ergibt sich:
Drei Seiten
Zwei Seiten
und ein Winkel
Zwei Seiten und
der eingeschlossene
Winkel
Zwei Seiten und
der Gegenwinkel
der längeren Seite
Eine Seite und
zwei Winkel
Zwei Seiten und
der Gegenwinkel
der kürzeren Seite
5
Übungen
1.
Berechne β:
a)
c)
b)
d)
6
Kantonsschule Solothurn
RYS SS14/15
Dreieckslehre
2. Ordne die folgenden Eigenschaften den Linien und Punkten in einem Dreieck zu:
I.
Der Punkt ist von B und C gleich weit entfernt.
II. Jeder Punkt ist gleich weit entfernt von A und B.
III. Der Punkt ist gleich weit entfernt von den Seiten a, b und c.
IV. Die Strecke teilt das Dreieck in zwei rechtwinklige Dreiecke.
V. Die Linie teilt das Dreieck in zwei flächengleiche Dreiecke.
VI. Der Punkt ist gleich weit entfernt von den Punkten A, B und C.
VII. Jeder Punkt ist gleich weit entfernt von den Seiten a und b.
3. Zeichne ein Dreieck ABC. Konstruiere einen möglichst grossen Kreis im Innern des
Dreiecks.
4. Zeichne ein beliebiges Dreieck ABC. Konstruiere einen Punkt, der von allen Eckpunkten A,
B, C gleich weit entfernt ist.
5. Gegeben sind drei Punkte A, B und C. Konstruiere einen Kreis, der durch die drei Punkte
geht.
6. Zeichne ein beliebiges Dreieck ABC. Konstruiere einen Punkt, der von allen Seiten a, b, c
gleich weit entfernt ist.
7. Zeichne ein Dreieck, bei dem der Inkreis- und der Umkreismittelpunkt zusammenfallen.
8. Gegeben ist ein beliebiges Dreieck ABC. Untersuche folgende Behauptung: Die
Winkelhalbierende wα schneidet die Mittelsenkrechte ma stets ausserhalb des Dreiecks.
7