Kürzeste Pfade in löchrigen Polygonen

Rheinische Friedrich-Wilhelms-Universität Bonn
Institut für Informatik I
Jasmin Kreutz
Kürzeste Pfade in
löchrigen Polygonen
1. Januar 2009
Seminararbeit im Wintersemester 08/09
Zusammenfassung
Wir haben uns im Rahmen des Seminars Algorithmische Geometrie / Algorithmische Bewegungsplanung im WS 2008/2009 mit dem
Thema Kürzeste Pfade in löchrigen Polygonen befasst. Dabei beschäftigen wir uns mit dem aunden von kürzesten Pfaden in löchrigen
Polygonen
P
und
n
P , wobei h die Anzahl der disjunkten Hindernispolygone in
P ist. Vorgestellt wird ein
die Gesamtzahl aller Ecken aus
Weg zur Berechnung, basierend auf dem Ansatz des schon bekannten
Algorithmus von Chen et al [1]. Der hier vorgestellte Algorithmus hat
den Vorteil, dass die Berechnungszeit an die Anzahl der Hindernisse
gebunden ist. Diese Seminararbeit basiert auf einem Auszug Shortest
Path Queries in Polygonal Domains [2] von Hua Guo, Anil Maheshwari
und Jörg-Rüdiger Sack 2008.
Inhaltsverzeichnis
1 Motivation
2
2 Grundlagen
2
2.1
Allgemeine Denitionen
. . . . . . . . . . . . . . . . . . . . .
3
2.1.1
Trichter
. . . . . . . . . . . . . . . . . . . . . . . . . .
3
2.1.2
Voronoidiagramm eines löchrigen Polygons . . . . . . .
4
2.1.3
Sanduhren . . . . . . . . . . . . . . . . . . . . . . . . .
4
2.1.4
Shortest Path Map . . . . . . . . . . . . . . . . . . . .
4
2.1.5
Skelettgraph
. . . . . . . . . . . . . . . . . . . . . . .
4
2.1.6
Lokaler kürzester Pfad . . . . . . . . . . . . . . . . . .
5
3 Verfahren
3.1
3.2
5
Ansätze für SSQ
. . . . . . . . . . . . . . . . . . . . . . . . .
5
3.1.1
Hershberger und Suri . . . . . . . . . . . . . . . . . . .
5
3.1.2
Kapoor et al
5
. . . . . . . . . . . . . . . . . . . . . . .
Ansätze für APQ . . . . . . . . . . . . . . . . . . . . . . . . .
5
3.2.1
Chen et al . . . . . . . . . . . . . . . . . . . . . . . . .
5
3.2.2
Chiang und Mitchell . . . . . . . . . . . . . . . . . . .
6
4 Grundlagen des Algorithmus
6
4.1
Zerlegungen . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7
4.2
Lokal kürzester Weg
. . . . . . . . . . . . . . . . . . . . . . .
8
4.3
Kritische Stelle
. . . . . . . . . . . . . . . . . . . . . . . . . .
8
5 Algorithmus
9
5.1
Vorbereitung
. . . . . . . . . . . . . . . . . . . . . . . . . . .
9
5.2
Weiterführende Ideen . . . . . . . . . . . . . . . . . . . . . . .
10
5.3
Anfrage
11
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1
1
Motivation
Wir werden uns mit der Frage nach der ezienten Suche von kürzesten Wegen in löchrigen Polygonen befassen. Ein löchriges Polygon kann man sich
dabei wie den Grundriss eines abgeschlossenen Raumes mit diversen Hindernissen vorstellen. Ein gutes Beispiel hierfür wäre ein Museum.
Säulen und Ausstellungsstücke kann man hier als Hindernisse betrachten,
während ein Besucher sich nicht auf festgelegten Wegen, wie in einem Straÿennetzwerk bewegen muss, sondern die ganze Restäche zur Verfügung hat.
Es ist einerseits interessant, den kürzesten Weg zwischen zwei beliebigen
Punkten zu berechnen, um eziente Führungen zu planen. Jedoch kann es
auch von Interesse sein, die kürzesten Wege von einem festgelegten Punkt
wie beispielsweise der Information zu den verschiedenen Attraktionen herauszunden.
Da wir von vielen verschiedenen Voraussetzungen ausgehen können, gibt es
auch verschiedene Lösungsverfahren. Die Kriterien zur Unterscheidung werden im Folgenden kurz angedeutet.
Diese sind die Vorbereitungszeit, also die benötigte Berechnungsdauer der
Hilfsstruktur, der Speicherbedarf dieser Suchstruktur und abschlieÿend die
Schnelligkeit, mit der eine gestellte Anfrage beantwortet werden kann.
Somit ist ein ezienter Algorithmus von den Spezikationen des Problems
abhängig. Es mag durchaus Situationen geben, in denen ein langsamerer Algorithmus mit geringem Speicherbedarf und kurzer Vorbereitungszeit einem
schnelleren mit langer Vorbereitungzeit und hohem Speicheraufwand vorgezogen wird.
2
Grundlagen
In vielen Gebieten beschäftigt man sich mit der Suche nach dem kürzesten
Pfad. Damit weiter gehend darauf eingegangen werden kann, benötigen wir
jedoch einige Grundlagen:
Denition 1
Punkten
u
und
Als kürzesten Pfad versteht man einen Weg zwischen zwei
v,
welcher um Hindernisse herum führt und eine minimale
euklidische Länge besitzt.
Ein kürzester Pfad von
u
nach
v
wird mit
des kürzesten Pfades ist die Distanz von
u
π(u, v) bezeichnet. Die Länge
v und wird mit dist(u, v)
und
benannt.
Dabei werden drei unterschiedliche Ansätze betrachtet.
•
SPQ (single-pair-query)
Bezeichnet eine Anfrage nach dem kürzesten Pfad zwischen zwei vor
der Berechnung der Queryanfrage festgelegten Punkten
2
u
und
v.
•
SSQ (single-source-query)
Bezeichnet eine Anfrage nach dem kürzesten Pfad von einem vorher festgelegten Startknoten
bei wird
u
u
zu einem beliebigen Endknoten
v.
Da-
vor der Berechnung der Vorverarbeitung festgelegt um die
Suchstrukturen aufzubauen, welche es ermöglichen, eine Anfrage zu
v
schnell zu beantworten.
•
APQ (all-pairs-query)
Bezeichnet eine Anfrage nach dem kürzesten Pfad zwischen zwei beliebigen Punkten
u
und
v.
Die Berechnung der Vorverarbeitung benötigt
somit keine Anfragepunkte mehr.
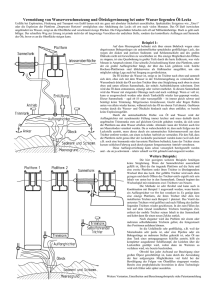
Kürzeste Pfade sind nicht immer eindeutig. In Umgebungen mit Hindernissen kann es vorkommen, dass zwei oder
mehr kürzeste Pfade gleicher Länge existieren (Abbildung
1). Hier ist der obere Pfad von
u
nach
v
genauso lang wie
der untere Pfad und beide Pfade sind die kürzesten.
Im Inneren eines einfachen Polygons ist der kürzeste Pfad
Abbildung
1:
gleichlange
kürzeste Pfade
jedoch immer eindeutig, da dort keine Hindernisse vorkommen, die auf mehrere Arten umlaufen werden können.
Im Folgenden gehen wir von löchrigen Polygonen und der Suche nach SSQ
und APQ aus.
2.1 Allgemeine Denitionen
In einigen der im folgenden Kapitel kurz vorgestellten Algorithmen werden
Verfahren zur Vorbereitung angewendet, die vielleicht nicht jedem bekannt
sind.
Daher versuchen wir eine kurze Einführung in die wichtigsten Methoden und
Hilfsmittel zu geben.
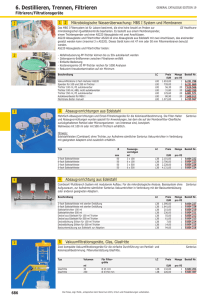
2.1.1 Trichter
Ein Trichter bildet sich aus den kürzesten Pfaden
zwischen einem Punkt
s
und einer diagonalen oder
l = pi pj eine Diagonale
P , nn wird die Vereinigung der kürzesten Wege f (s, l) = π(s, pi ) ∪ π(s, pj )Trichter genannt.
Ein Trichter ist oen, wenn sich π(s, pi ) und π(s, pj )
nur in einem Punkt s berühren. Wenn sich die kürpolygonalen Kante. Sei
in
zesten Pfade in mehr als einem Punkt überschnei-
Abbildung 2: geschlossener Trichter
den, so wird der Trichter als geschlossen bezeichnet (Abbildung2).
3
2.1.2 Voronoidiagramm eines löchrigen Polygons
P werden Besitzer S genannt. Dabei ist
S = {v1 , v2 , ..., vn ; e1 , e2 , ..., en }. Jedem dieser Besitzer kann eine eindeutige
Zelle zugeordnet werden. In der Zelle zu Si liegt jeder Punkt dieser Zelle
näher an Si als an jedem anderen Element aus S .
Kanten und Ecken aus
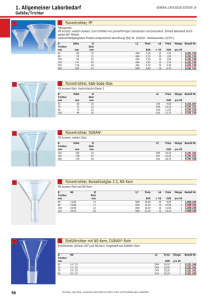
2.1.3 Sanduhren
Eine Sanduhr bildet sich aus den kürzesten Pfaden
zwischen zwei Diagonalen.
Seien li = pi pi+1 , lj = pj pj+1 zwei
P , die Vereinigung
H(li , lj ) = π(pi , pj ) ∪ π(pi+1 , pj+1 )
Diagonalen in
wird Sanduhr
genannt.
Eine Sanduhr wird als oen bezeichnet, falls
und
π(pi+1 , pj+1 )
π(pi , pj )
Abbildung 3: Sanduhr
keine gemeinsamen Segmente besitzen, andernfalls gilt sie
als geschlossen (Abbildung 3).
2.1.4 Shortest Path Map
Vom Startpunkt aus wird eine Welle
losgeschickt, diese breitet sich kreisförmig aus und bildet die erste Zelle der SPM. Ein kürzester Pfad zu
einem Punkt innerhalb dieser Zelle
wird auf direktem Weg erreicht, da
Start- und Zielpunkt Sichtkontakt
zueinander besitzen. Wenn die Welle auf eine Hindernisecke trit, so
bildet sich von dieser Ecke des Hin-
Abbildung 4: SPM
dernisses eine neue Welle aus. Diese
erzeugt die nächste Zelle in der SPM. Jeder Weg vom Start zu einem Punkt
dieser Zelle führt folglich über den Eckpunkt des Hindernisses. Zur Berech-
O(nlog 2 n) Zeit und O(nlogn) Platz benötigt. Jedoch
Algorithmus im Mittel mit O(nlogn) Zeit und O(nlogn) Platz
nung wird im worstcase
kommt der
aus (Abbildung 4).
2.1.5 Skelettgraph
G = (V, E) auf P bildet sich aus dem Voronoidiagramm
P . Dabei werden von dem Diagramm alle Kanten, die inzident zu P sind,
weggelassen. Inzident bedeutet hierbei, dass die Voronoikante P berührt.
Ein Skelettgraph
von
4
2.1.6 Lokaler kürzester Pfad
Wir triangulieren
P.
Seien
u
und
v
Anfragepunkte, so ist
π(u, v)
ein Pfad
P
in einer eindeutigen Reihenfolge. Es existiert also ein Pfad zwischen u und v ,
auf dem Skellettgraph. Dieser schneidet die Kanten der Triangulation von
der die Diagonalen in eine Folge zerteilt. Als lokal kürzesten Pfad bezeichnen
wir den Pfad mit minimaler euklidischer Länge, der die Folge von Diagonalen
in genau der selben Reihenfolge schneidet.
3
Verfahren
3.1 Ansätze für SSQ
3.1.1 Hershberger und Suri
Hershberger und Suri [2] entwickelten einen Algorithmus zur Berechnung einer SPM (shortest path map). Diese Karte bietet alle kürzesten Wege in
P
von einem bestimmten Startpunkt aus.
Im Mittel werden zur Berechnung
O(nlogn)
Platz und
O(nlogn)
Zeit benö-
tigt. Abfragen eines bestimmten Pfades werden mit dem Dijkstra Algorithmus in
O(nlogn)
beantwortet.
3.1.2 Kapoor et al
Kapoor et al [3] erstellten einen Algorithmus mit Hilfe von Sichtbarkeitsgraphen. Dafür berechneten sie zuerst die Triangulation der Fläche
punkt
u
und Zielpunkt
v
P.
Start-
müssen nun in einem der Dreiecke liegen oder auf
dem Rand eines solchen. Sollten sie in demselben Dreieck liegen, ist der kürzeste Pfad eine direkte Verbindung der beiden Punkte.
Nun werden alle Eckpunkte des Dreiecks von
gesetzt, ebenso mit
v.
u
mit diesem in Verbindung
Danach wird der duale Graph der Triangulation er-
zeugt. In diesem können alle Knoten mit Grad eins gelöscht werden, sofern
sie nicht
u
oder
v
beinhalten.
Wird nun ein kürzester Weg von
u nach v
gesucht, so kann über die Triangu-
lation eine Sanduhr gebildet werden. Alle Punkte auf den beiden Endgraden
haben ihren kürzesten Weg durch die Trichter. Mit Hilfe der Sichtbarkeitsgraphen kann dann eine SPM in der Zeit von
O(n + h2 logn)
berechnet werden.
3.2 Ansätze für APQ
3.2.1 Chen et al
P mit einer Vorbereitungszeit von O(n2 logn)
2
und einem Platzbedarf von O(n ) eine APQ in O(min(Qa , Qb )logn) berechnet werden kann. Hierbei ist Qa die Anzahl der sichtbaren Knoten von a und
Qb die Anzahl der sichtbaren Knoten von b.
Chen et al [4] zeigten, dass in
5
3.2.2 Chiang und Mitchell
Chiang und Mitchell [5] entwickelten einen Algorithmus, der zwar eine Vorer-
O(n11 ) besitzt, dafür eine beliebige
arbeitungszeit und einen Platzbedarf von
O(logn) beantwortet. Eine weitere
O(n10 logn) Platz und O(n10 logn) Zeit
2
in einer Zeit von O(log n).
Anfrage im Bestfall in
Abart dieses Al-
gorithmus benötigt
und beantwortet
eine Anfrage dafür
4
Grundlagen des Algorithmus
Nun zu dem Ansatz im nächsten Kapitel, mit dem sich diese Ausarbeitung
hauptsächlich befassen soll.
Der Trick ist hier Reduktion. Während ein Punkt
Umgebung von
P
u
überall in der freien
liegen kann, müssen die kürzesten Wege über die Ecken der
Hindernisse laufen, sofern sich Start- und Zielpunkt (v ) nicht direkt sehen.
Daher wird in der Vorbereitung für jedes
das löchrige Polygon
P
n eine SPM erzeugt. Ebenfalls wird
mit einer ganz speziellen Zerlegung in eine Menge
von Dreiecken und einfachen Polygonen aufgeteilt. Der Vorteil an diesem
Verfahren ist, dass die Zerlegung eindeutig und der reduzierte Skelettgraph
statisch ist.
Diese Berechnungen bilden eine Datenstruktur der Gröÿe
O(n2 ) in O(n2 logn)
Zeit. Zum Lösen einer Anfrage benötigt dieses Verfahren in Abhängigkeit von
der Anzahl der Hindernisse eine Zeit von
O(hlogn).
Um den Algorithmus besser zu verstehen, müssen wir vorher auf einige Besonderheiten des Algorithmus eingehen. Wichtig ist die Art der Zerlegung,
das Wissen um den lokalen kürzesten Pfad und um die kritischen Stellen.
Abbildung 5: links: das Voronoidiagramm von
SP
6
P,
rechts: der Skelettgraph
4.1 Zerlegungen
VP
Zuerst erzeugen wir das Voronoidiagramm
von
P
(Abbildung 5). Wir
gehen davon aus, dass die Hindernisse in allgemeiner Lage liegen. Daher
haben wir im Voronoidiagramm keine Knoten mit einem Grad gröÿer als 3.
Danach wird durch Löschung inzidenter Kanten zu
VP
aus
P
der Skelettgraph
SP
gebildet (Abbildung 5). Alle Knoten des Skelettgraphen können nun
Grad 1-3 enthalten.
Im trivialen Fall hat
P
keine Hindernisse, dann ist das Problem auf kürzeste
Pfade in einfachen Polygonen zu reduzieren. Im Normalfall muss mindestens
ein Hindernis in
P
existieren. Damit gibt es in
SP
wenigstens einen Kreis
um dieses Hindernis herum. Damit ist der Graph zusammenhängend, und es
muss folglich ein Weg zwischen zwei beliebigen Knoten des Skelettgraphen
SP
existieren.
u
Wenn wir nun einen Pfad zwischen zwei Punkten
und
v
so können wir diesen auf einen Pfad zwischen zwei Punkten
dem Skelettgraphen zurückführen. Dabei ist
su
Skelettgraphen mit dem kleinsten Abstand zu
Nun erstellen wir aus dem Skellettgraph
SP
P
aus
su
suchen,
und
sv
auf
der Punkt auf der Kante des
u,
selbiges gilt für
sv
v.
GP
und
den reduzierten Skelletgraph
(Abbildung 6).
Dabei werden alle Knoten und dazu gehörenden Kanten des Skelettgraphen
mit Grad 1 entfernt, übrig bleiben somit noch Knoten mit Grad 2 oder 3.
Nun werden alle Knoten vom Grad 2 durch eine einzige Kante ersetzt. Etwas
ausführlicher:
a, b, c Knoten, (a, b), (b, c) Kanten und hat b den Grad 2, also nur a
c als Nachbarn, so wird eine Kante (a, c) eingefügt und anschlieÿend
sowohl Knoten b wie auch die Kanten (a, b) und (a, c) gelöscht.
Sind
und
Somit bleibt nur noch ein Graph, der aus Knoten des Grades 3 besteht.
Da wir
h
Hindernisse haben und dieser reduzierte Skelettgraph um jedes
dieser Hindernisse einmal herumläuft, existieren also
Abbildung 6: links: der reduzierte Skelettgraph
gung von
P
in
P0
7
GP
h+1 Flächen. Zu jedem
von
P,
rechts: die Zerle-
x aus dem reduzierten Skelettgraph GP existiert ein Dreieck, welches
x assoziierten Besitzern aus P gebildet werden kann. Jeder Knoten
hat genau drei Besitzer, über diese wird ein Dreieck gebildet, ohne dabei GP
zu schneiden. Das Polygon P wird somit in eine Menge aus Dreiecken und
0
einfachen Polygonen zerlegt. Die Zerlegung wird im Folgenden P genannt
Knoten
mit den zu
(Abbildung 6).
Alle Kanten zwischen zwei Dreiecken oder zwischen einem Dreieck und einem
Polygon werden Gates genannt. Die komplette Zerlegung geht in einer Zeit
von
O(n).
4.2 Lokal kürzester Weg
Wir nehmen
u und v als zwei Anfragepunkte in P . In der Zerlegung von P
aus
4.1 liegen diese Punkte entweder in einem Dreieck oder in einem einfachen
Polygon
su
R(i).
SP reduziert.
su nach sv existieren.
Legen wir den Skelettgraph SP über das Voronoidiagram VP , so existiert
auf der linken und der rechten Seite von SP eine eindeutige Abfolge von
Voronoizellen. Sei φ(su , sv ) der Weg mit dem kürzesten euklidischen Abstand
und
sv
Diese Punkte werden wie in 4.1 beschrieben auf die Punkte
auf dem Skelettgraphen
Es können mehrere Pfade von
über derselben Abfolge von Voronoizellen, so ist es ein lokal kürzester Pfad.
Die Ecken des Pfades auf dem Skelettgraphen werden mit den Ecken auf
dem lokal kürzesten Pfad assoziiert. Jeder Knoten des Pfades kann nur seine
direkten Nachbarn sehen.
4.3 Kritische Stelle
Eine kritische Stelle ist der letzte sichtbare Knoten von
zesten Weges. Ein Punkt
v
v
entlang eines kür-
kann mehrere kritische Stellen besitzen, diese
sind die Ecken aus P.
Angenommen, wir haben eine Orientierung von
πφ (u, v)
gegeben.
Wenn sich beide Punke gegenseitig sehen, so ist die direkte Verbindung zwischen
u
u
und
v
der kürzeste globale Weg. Andernfalls wird der letzte von
sichtbare Knoten als kritische Stelle bezeichnet. Hierdurch teilt sich die
Sequenz der assoziierten Knoten in zwei geordnete Folgen, in die Folge der
Knoten, die von
v
aus sichtbar sind und in die Folge der Knoten, die von
v
aus nicht sichtbar sind.
Klar ist, dass eine solche kritische Kante selbst beim trivialen Fall existieren
v die kritische Stelle zu u und umgekehrt. Andernfalls
Weg zwischen u und v möglich.
muss, in diesem Fall ist
wäre kein kürzester
8
5
Algorithmus
Nun zum Algorithmus, dieser soll in Zeit
Datenstruktur bilden, mit der eine APQ
O(n2 logn) und Platz O(n2 ) eine
in O(hlogn) beantwortet werden
kann.
5.1 Vorbereitung
Wir gehen davon aus, dass
u
und
v
sich nicht gegenseitig sehen, da der kür-
zeste Pfad sonst eine direkte Verbindung wäre. Die Menge der kritischen
Stellen für
u
soll
Cu
sein und
Ein kürzester Pfad von
kritische Stelle aus
Cu
u
Cv die Menge der
v muss folglich
nach
kritischen Stellen für
in
u
v.
starten und über eine
laufen. Dann führt er weiter und kommt schlieÿlich
Cv zum Ziel v .
Für jede kritische Stelle c ∈ Cu ∪ Cv berechnen wir mit der passenden SPM
die Entfernung dist(c, u) und dist(c, v). Damit ist dist(c, u) + dist(c, v) die
Länge eines Pfades über c. Der kürzeste Weg dist(u, v) ist damit das Minimum aller Pfadlängen für alle c ∈ Cu ∪ Cv
über eine kritische Stelle aus
dist(u, v) = minc∈Cu ∪Cv (dist(u, c) + dist(c, v))
Es ist ausreichend nur eine der beiden Mengen
Cu
und
Cv
zu betrachten, da
es einerlei ist, ob alle Präxe des lokalen kürzesten Pfades gesucht werden,
der u verlässt oder alle Suxe der lokalen kürzesten Pfade, die v erreichen.
Cmin ist nun die kleinere der beiden Mengen Cu und Cv , dann gilt
dist(u, v) = minc∈Cmin (dist(u, c) + dist(c, v))
Der Einfachheit halber gehen wir weiter davon aus, dass
Cu
Cmin
im Folgenden
sei. Wir wenden den Algorithmus 5.1 an. Dieser benötigt keine Eingaben
von Anfragepunkten sonder nur die Polygonszene, daher reicht es uns, diesen einmal anzuwenden. Der Algorithmus zerlegt die Szene, so dass spätere
Anfragen schnell bearbeitet werden können, da bei neuen Anfragen auf die
schon gespeicherte Datenstruktur zurück gegrien wird.
VP , der Skelettgraph SP , der re0
duzierte Skelettgraph GP , die Zerlegung P , die einfachen Polygone R(l1 , l2 ),
Damit wurden nun das Voronoidiagramm
die Hierarchie der Sanduhren
HH(R),
die Sanduhren
lich die pointlocation Struktur berechnet.
Dies alles in
O(n2 )
Platz und
O(n2 logn)
9
Zeit.
H(l1 , l2 )
und schlieÿ-
Algorithmus 5.1 APQ PD Preprocessing(P )
Input: ein löchriges Polygon mit
h
Hindernissen und
n
Ecken
Output: Datenstruktur für APQ(P )
1.
∀v ∈ P
berechne SPM(v )
VP von P .
VP .
4. berechne den reduzierten Skelettgraph GP auf SP .
0
5. berechne die Zerlegung P von P .
6. berechne/speichere für alle einfachen Polygone R(l1 , l2 )
Gates l1 und l2 eine Hierarchie der Sanduhren, HH(R).
7. speichere H(l1 , l2 )
2. berechne/speichere Voronoidiagramm
3. berechne den Skelettgraph
SP
aus
in
P0
mit den
8. berechne eine pointlocation Struktur basierend auf der Triangulation
(Punkt 5).
5.2 Weiterführende Ideen
In der Vorverarbeitung wurden viele Strukturen erstellt, diese greifen bei
einer Anfrage ineinander und reduzieren den Zeitaufwand erheblich. Beim
eigentlichen Anfrageteil, der im wesentlichen aus der Verkettung von Trichtern besteht, werden zusätzlich noch für die beiden Anfragepunkte
u
und
v
Listen oener und geschlossener Trichter geführt.
Fo (u)
ist die Menge der oenen Trichter zwischen
Fc (u) die
Fc (v) sind
verarbeitung berechneten Nachbargates,
Trichter von
u
zu den Gates.
Fo (v)
und
u
und den in der Vor-
Menge der geschlossenen
die Trichtermengen für
v
zu den angrenzenden Gates.
Der Anfragealgorithmus arbeitet über die Struktur von oenen Trichtern in
alle Richtungen, bis er entweder eine Lösung errechnen konnte oder aber
keine oenen Trichter in den Listen
Fo (u)
und
Fo (v)
mehr existieren. Was
bedeutet, dass es keine weiteren Wege mehr gibt und alles schon berechnet
wurde.
In diesem Algorithmus ist die Trichterstruktur ein BST oder auch balanzierter binärer Baum (engl. balanced binary search tree).
Bei der Trichterverkettung können zwei Fälle auftreten.
Benden wir uns in einem einfachen Polygon, so besitzt dieses dank unserer
Zerlegung genau zwei Gates. Sind wir in einem Dreieck, dann können entweder zwei oder drei Gates vorhanden sein. Zwei Gates, wenn das Dreieck
nicht direkt durch einen Punkt des reduzierten Skelettgraphen gebildet wurde, drei, wenn das Dreieck zu einem Punkt des reduzierten Skelettgraphen
gehört.
Zur Erläuterung:
u ein einfaches Polygon R(l1 , l2 ),
f (u, l1 ) mit der Sanduhr H(l1 , l2 ) des Polygons.
den Trichter f (u, l2 ).
Liegt angrenzend an unserem Eingabepunkt
so verketten wir den Trichter
Als Ergebnis bekommen wir
10
u ein Dreieck ∆l1 , l2 , l3 , dann
f (a, l1 ) mit ∆l1 , l2 , l3 . Hier kann es zu einem Trichtersplit kom-
Liegt angrenzend an unseren Eingabepunkt
verketten wir
men, dabei teilt sich der Trichter nun in zwei verschiedene Richtungen auf.
Einmal verketten wir es zu l2 und einmal zu l3 , somit besitzen wir nun zwei
Endtrichter. Die Berechnung der neuen Trichter nennt sich ziehen. Als Ergebnis bekommen wir die zwei neuen Trichter
f (a, l2 )
und
f (a, l3 ).
Um Trichter nicht doppelt zu benutzen wird ein DAG (directed azyclic
graph) erzeugt. Dieser bildet sich aus dem reduzierten Skelettgraphen
GP .
Jede Kante wird gerichtet, um die Abhängigkeiten der Trichter zu repräsentieren. Jeder Knoten von
GP
speichert einen Pointer, der auf das Gate zeigt,
welches vom Trichter besucht wurde.
Somit repräsentiert eine gerichtete Kante
(u(l1 ), v(l2 ))
eine Trichterverket-
tung von Gate l1 zu Gate l2 .
Um dies zu berechnen, wird eine Folge von nutzbaren Knoten erzeugt. Dabei gilt: zwei Knoten
v1 (l1 )
wenn sie zu einem Dreieck
v2 (l2 ) sind Geschwister
∆(l, l1 , l2 ) in P 0 gehören.
und
mit dem Vater
u(l),
Um herauszunden, welche Knoten markiert werde müssen, testen wir für
jeden Knoten, ob dessen Vater- und Geschwisterknoten schon markiert wurden, , Falls dem so ist wird auch dieser Knoten markiert. Wenn alle Knoten
getestet sind und keine Veränderung der Folge mehr auftritt, startet die
Trichterverkettung. Wird ein Trichter verkettet, so wird der dazugehörige
Knoten aus der Folge entfernt. Solange die Folge noch nicht leer ist, wird der
Trichter weiter verkettet.
Die besondere Grundidee dieses Algorithmus besteht darin, dass nur O(1)
Trichter für jedes Gate propagiert werden.
Zur weiteren Berechnung hier noch ein Algorithmus zur Erkennung der pas-
Cmin oder
dist(a, b) ausgeben. In diesem Algorithmus wird O(h) mal
konkatiniert, O(1) mal für jedes Gate und O(h) mal für das ziehen. Die
Anzahl der Iterationen ist durch O(h) begrenzt. Jede Iteration benötigt dabei im worstcase eine Zeit von O(logn).
senden kritischen Stellen. Er soll als Ausgabe entweder die Menge
aber die Distanz
Die Berechnung eines kürzesten Pfades dauert somit im worstcase eine Zeit
von
O(hlogn).
5.3 Anfrage
u und v in Form
dist(u, v) ausgeben. Mit
der Hilfestruktur zur Pointlocation ndet er zuerst das Dreieck fu zu u und
fv zu v . Als nächstes wird in der Zerlegung P 0 nach den Regionen R(u) und
R(v) gesucht, welche u und v enthalten.
Der Anfragealgorithmus bekommt die zwei Anfragepunkte
eines Tupels
(u, v)
als Eingabe und soll die Distanz
Es muss nicht unterschieden werden, ob Punkte im Inneren oder auf den Rändern der Regionen liegen. Wenn Punkte auf den Rändern oder aber direkt
auf Diagonalen liegen dann wird der Punkt einer der beiden Nachbarregio-
11
nen zugeordnet. Hier können zwei Fälle auftreten.
Fall 1.
Die Regionen
R(u)
dies bedeutet, dass
und
u
R(v) sind identisch,
v entweder im sel-
und
ben Dreieck oder aber im selben einfachen Polygon liegen. Sollten sie sich im selben Dreieck
der Zerlegung
P0
benden, dann ist der kürzes-
te Pfad die direkte Verbindung von
Dann kann die Distanz
dist(u, v)
u
und
v.
Abbildung 7:
R(u)=R(v)
ohne groÿen
Aufwand berechnet und ausgegeben werden.
Sollten beide Punkte in einem einfachen Polygon liegen, so wird geprüft, ob
sie sich sehen. Ist dies der Fall, wird ebenfalls die Distanz
dist(u, v)
berech-
net und ausgegeben. Interessanter ist der Fall, wenn sie sich innerhalb des
Polygons nicht sehen. Dann muss der kürzeste Pfad über eine Ecke des Polygons laufen. Seien nun lu und lv die Diagonalen, welche
u und v am nächsten
liegen. Nun verkettet der Algorithmus den Trichter f (u, lu ) mit der Sanduhr
H(lu , lv ) und weiter mit dem Trichter f (lv , v) (Abbildung 7).
Die resultierende Sanduhr H(u, v) ist geschlossen, da sich die Punkte nicht
direkt sehen konnten.
Fall 2
Hier liegen
u
und
v
in unterschiedlichen Regionen. Diese können entweder
zwei Dreiecke, zwei einfache Polygone oder aber ein Dreieck und ein Polygon
sein.
Zur Vereinfachung sei
Wenn
schen
i
i
i ∈ {u, v}.
nun ein Dreieck ist, so berechnet der Algorithmus alle Trichter zwi-
l1
f (i, l2 ) .
und seinen angrenzenden Gates
liefert als Teilergebnis
Sollte es sich bei
f (i, l1 )
R(i)
und
und
aus der Region
R(i).
Er
um eine einfaches Polygon handeln, so werden erst
die beiden Diagonalen gefunden, die dem Punkt
li1 und li2
H(l2 , li2 ) zwischen
l2
i
am nächsten liegen. Diese
H(l1 , li1 )
werden mit
bezeichet. Danach werden die Sanduhren
und
den Gates l1 und l2 und den Diagonalen berechnet.
Dabei ist es egal, ob es sich bei
R(i)
um ein Dreieck oder um ein einfaches
Polygon handelt, es werden in beiden Fällen Trichter berechnet.
Diese Trichter werden auf Oenheit geprüft. Da führt der Algorithmus drei
Hilfsstrukturen mit sich. Eine Liste für oene Trichter
geschlossene Trichter
Fc (i)
Fo (i),
eine Liste für
und einen DAG, in dem die oenen Trichter ver-
waltet werden können. Falls die resultierenden Trichter oen sind, so fügt
der Algorithmus sie der Menge der oenen Trichter
der Menge der geschlossenen Trichter
Nun muss noch der DAG
D(i)
Fo (i)
hinzu, andernfalls
Fc (i).
aktualisiert werden. Schlieÿlich wird der Al-
12
Algorithmus 5.2 FindMinCriticalSites
(u, v), die Menge der oenen und geschlossen TrichFo (u), Fc (u), Fo (v), Fc (v), die DAGs der oenen Trichter D(u), D(v)
0
und die Zerlegung P .
Output: entweder die Menge der kritischen Stellen Cmin oder die Distanz
von u und v dist(u, v).
Cmin sei leer.
while Fo (u), Fo (v) sind nicht leer do
Input: ein Anfragepaar
ter
2.1
es fallen für jedes nutzbare Gate lu zwei Fälle an
if
lu
if
inzident zu einem Nachbardreieck
v
if
v
then
then
berechne
dist(u, v)
∆lu , l1 , l2
ist
then
ist in lu , l1 , l2
u
sieht
end if
end if
und gebe es aus.
ziehe einen Trichter oder aber zwei Trichter, diese bilden neue
Endtrichter für die beiden Gates l1 und l2 .
end if
if lu inzident zu einem einfachen Polygon ist then
if R enthält v then
H(lu , lv1 ) in R
propagiere den Endtrichter von lu und die assoziierte Sanduhr nach
lv1 mittels Verkettung von H(lu , lv1 )
identiziere die Sanduhr
if
der Trichter ist oen
if
u
sieht
berechne
end if
end if
end if
then
v
dist(u, v)
then
und gebe es aus.
verkette den oenen Trichter nach
end if
v.
2.2
verkette den Endtrichter von
lu
und die assoziierte Sanduhr zu allen
Nachbargates. Falls der Trichter sich schlieÿt, dann ziehe einen neuen
Endtrichter. lösche alle geschlossenen Trichter aus
Fo (u)
und
Fo (v)
und
D(v)
2.2 für v
aktualisiere den DAG
wiederhole 2.1 und
end while
Fo (u) leer sein. Für jeden Trichter in Fc (u) sammle den ersten Knoten
speichere ihn in Cmin . Gebe Cmin zurück.
lasse
und
13
gorithmus FindMinCriticalSites mit
Fo (i)
und
Fc (i)
aufgerufen. Dieser Al-
gorithmus kann wie oben beschrieben entweder die Distanz
dist(u, v)
als
Ergebnis liefern, dann können wir diese direkt ausgeben, oder er liefert uns
die Menge der kritischen Stellen
Cmin .
Wenn wir
Cmin
bekommen haben,
werden über die SPMs alle möglichen Wege berechnet. Danach wird das Minimum dieser Wege gesucht, der kürzeste Weg ist nun gefunden.
Literatur
[1] D.Z. Chen, O. Daescu, and K.S. Klenk. On geometric path query problems, 1997.
[2] H. Guo, A. Maheshwari, and J.R. Sack. Shortest path queries in polygonal domains, aaim 2008.
[3] S. Kapoor, S.N. Maheshwari, and J.S.B. Mitchell. An ecient algorithm
for euclidean shortest paths among polygonal obstacles in the plane.,
1997.
[4] J. Hershberger and S. Suri. An optimal algorithm for euclidean shortest
paths in the plane, siam journal on computing vol28, 1999.
[5] Y.J. Chiang and J.S.B Mitchell. Two-point euclidean shortest path queries in the plane., 1999.
14