Dagstuhl Lehrerfortbildung
Werbung

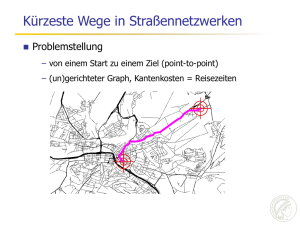
Über Routenplanung und Suchmaschinen Holger Bast Max-Planck-Institut für Informatik Saarbrücken, Germany Vorlesung zur Lehrerweiterbildung in Informatik Schloss Dagstuhl, 14. Dezember 2007 Meine Gruppe am MPI Informatik Bis vor kurzem – 2 Doktoranden, 5 Diplomanden, 2 Hilfskräfte Debapriyo Majumdar Ingmar Weber Alexandru Chitea Henning Peters Gabriel Manolache Marjan Celikik Ivan Popov Markus Tetzlaff Daniel Fischer Kooperationen innerhalb des MPII Kooperationspartner aus den letzten 3 Jahren Überblick Teil 1: Routenplanung – Grundlagen: Dijkstras Algorithmus – kurze Pause – Fortgeschrittenere Verfahren Pause Teil 2: Suchmaschinen – wir bauen eine Suchmaschine – kurze Pause – CompleteSearch genug Zeit für Diskussionen und Fragen! Teil 1: Routenplanung Grundlegendes – Dijkstras Algorithmus (10 min) – Korrektheitsbeweis (10 min) – Bidirektionaler Dijkstra (5 min) – Warum nicht ausreichend (5 min) Techniken zur Beschleunigung – A* + Landmarks (10 min) – „Straßenschilder” (10 min) – Highway Hierarchies (10 min) – Transitknoten Routing (10 min) Pause! Das Kürzeste Wege Problem 3 Gegeben ein Netzwerk – Knoten und (gewichtete) Kanten 1 2 2 1 2 3 1 Berechne den kürzesten Weg – zwischen zwei Knoten s und t (point to point, P2P) – von einem Knoten s aus zu allen anderen (single source shortest path, SSSP) – zwischen allen Knotenpaaren (all-pairs shortest path, APSP) Dijkstras Algorithmus Absolut grundlegend – kein Navigationsgerät und keine „Maps” Applikation, bei der nicht in irgendeiner Phase dieser Algorithmus verwendet wird – löst das single-source shortest-path (SSSP) Problem – point-to-point (P2P) Problem nicht einfacher Erfinder – Edsger Dijkstra, 1930 – 2002 Demo – http://www.unf.edu/~wkloster/foundations/DijkstraApplet/Dijks traApplet.htm Dijkstras Algorithmus — Pseudo Code 1 2 3 4 5 6 7 8 9 10 for each node u dist[u]: = infinity dist[s] := 0 PQ = all nodes while PQ is not empty u := node from PQ with smallest (get and remove it) for each neighbor v of u d := dist[u] + cost(u,v) if d < dist[v] dist[v] := d die einzige nicht-triviale Operation dist[u] Dijkstras Algorithmus — Korrektheit Betrachte ein Ziel t und den kürzesten Weg dorthin v u t s Definiere – dist(s,u) = Kosten des kürzesten Weges von s nach u Angenommen dist[t] ≠ d(s,t) 1. sei u der erste Knoten von s aus mit dieser Eigenschaft 2. sei v der Knoten davor, somit dist[v] = d(s,v) ≤ d(s,u) < dist[u] 3. dann ist v vor u bearbeitet worden (in Zeile 6) 4. dann ist dist[u] ≤ dist[v] + cost(v,u) = d(s,u) Widerspruch zu 1. Dijkstras Algorithmus — Laufzeit Zeile 6 – die Operation heißt delete-min – wird genau einmal für jeden der n Knoten ausgeführt Zeilen 8 – 10 – die Operation in Zeile 10 heißt decrease-key – wird höchstens einmal für jede der m Kanten ausgeführt Insgesamt also – n * cost(delete-min) + m * cost(decrease-key) – trivial: cost(delete-min) ~ n und cost(decrease-key) ~ 1 – geht auch: cost(delete-min) ~ 1 und cost(decrease-key) ~ log n – Laufzeit dann ~ n + m * log n Straßengraphen … … sind auch Netzwerke – Knoten = Kreuzungen – Kanten = Straßen – Kantengewichte = Reisezeiten Typische Straßengraphen – USA: 24 Millionen Knoten, 58 Millionen Kanten – Westeuropa: 18 Millionen Knoten, 42 Millionen Kanten – Deutschland: 4 Millionen Knoten, 11 Millionen Kanten Mit Dijkstras Algorithmus – durchschnittliche Zeit für zufällig gewähltes Start und Ziel: mehrere Sekunden auf ganz USA oder Europa Wie kann man das beschleunigen? Bidirektionaler Dijkstra Dijkstra kann man sich auch so vorstellen – bei Entfernung d – werden d2 Knoten besucht Bidirektionaler Dijkstra – bei Entfernung d – werden 2 * (d/2)2 = d2/2 Knoten besucht Gewinn nur grob ein Faktor 2 Der A* (A-Stern) Algorithmus Für ziel-orientiertere Suche (auf einen Knoten t hin) – Annahme: für jeden Knoten u ein Wert h[u] der schätzt wie weit es von dort zum Ziel ist – Bedingung: h[u] unterschätzt die Entfernung zum Ziel Algorithmus – wie Dijkstra, aber Reihenfolge der Knoten (Zeile 6) nicht gemäß dist[u] sondern gemäß dist[u] + h[u] – wenn all h[u] = 0 gerade Dijkstra Algorithmus A* Algorithmus — Korrektheit Selbe Idee wie bei Dijkstra v s Aber aufpassen – Übungsaufgabe … u t A* Algorithmus — wie schätzen? Einfacher Schätzer: – Luftlinie zum Ziel mit Autobahngeschwindigkeit – nicht sehr effektiv Landmarks – ca. 20 strategisch wichtige Punkte auf der Karte – für jeden solchen Punkt L untere Schranke max(d(s,L) – d(t,L) , d(t,L) – d(s,L)) [Bild malen!] – von 1 Sekunde 1 Millisekunde (auf dem Straßengraphen der USA der Westeuropas) Erfinder – Andrew Goldberg, Microsoft Research Highway Hierarchies Idee: Auf langen Reisen fährt man (meistens) – erst auf die nächste Hauptstraße – dann auf Bundesstraßen – dann auf Autobahnen – und in der Nähe des Ziels dasselbe anders herum Algorithmus (High-Level) – berechne eine Hierarchie von wichtigeren und wichtigeren Straßen, mit der Garantie dass die Strategie oben immer zum optimalen Weg führt – von 10 Millisekunden 1 Millisekunde Erfinder – Peter Sanders (lange MPI Informatik, jetzt U. Karlsruhe) – Dominik Schultes (Doktorand von P. Sanders) http://algo2.iti.uni-karlsruhe.de/schultes/hwy/demo/applet.html Transitknoten Sehr einfache Grundidee – wenn man weit weg fährt, verlässt man seine nähere Umgebung durch einen von relativ wenigen Verkehrsknotenpunkten – versuche diese Knotenpunkte (= Transitknoten) vorzuberechnen – und alle paarweisen Distanzen zwischen ihnen Das mit Abstand schnellste Verfahren – von 1 Millisekunde 10 Mikrosekunden (für das Straßennetzwerk der USA oder Westeuropas) Erfinder – Holger Bast & Stefan Funke, MPI Informatik Transitknoten — Vorberechnung Vorberechnung weniger Transitknoten – mit der Eigenschaft, dass jeder kürzeste Pfad über eine gewisse Mindestdistanz durch einen Transitknoten geht Vorberechnung der nächsten Transitknoten für jeden Knoten – mit der Eigenschaft, dass jeder kürzeste Pfad über eine gewisse Mindestdistanz von diesem Knoten aus durch ein dieser nächsten Transitknoten geht Vorberechnung aller Distanzen – zwischen allen Paaren von Transitknoten und von jedem Knoten zu seinen nächsten Transitknoten Suchanfrage = wenige table lookups ! Pause Teil 2: Suchmaschinen Wir bauen eine Suchmaschine (live) – Crawling (5 min) – Parsing (10 min) – Invertierung (5 min) – Suchanfragen (10 min) – Web interface (5 min) Die CompleteSearch Suchmaschine – Prinzip am Beispiel erklären (10 min) – was man damit alles machen kann (20 min) – Datenstrukturen + Experimente (10 min) Pause! Webseiten herunterladen (Crawling) Eingabe – eine Liste von URLs Ausgabe – HTML Dateien, eine für jede der URLs Implementierung – wir benutzen einfach curl (oder wget) Zerlegung in Worte (Parsing) Eingabe – die HTML Dokumente aus dem Crawling Ausgabe – eine Textdatei index.words mit Zeilen der Form Wort Dokumentennummer dies ist ein satz 15 15 15 15 – eine Textdatei index.docs mit Zeilen der Form Dokumentennummer URL 15 16 http://www.dagstuhl.de/abc http://www.dagstuhl.de/xyz Invertierung Eingabe – die (Wort, Dokumentennummer) Paare nach Dokumentennummer sortiert Ausgabe – dieselben Paare nach Worten sortiert (und innerhalb desselben Wortes nach Dokumentennummer) – damit bekommen wir so etwas wie den Index am Ende eines Buches, aber für jedes Wort – ein sogenannter Volltextindex Suchanfragen (Queries) Eingabe – eine Liste von Worten (durch Leerzeichen getrennt) Ausgabe – die Liste aller Dokumente, die alle diese Worte enthalten Implementierung – für jedes Wort holen wir uns die vorberechnete Liste aller Nummern von Dokumenten, die es enthalten – dann berechnen wir die Schnittmenge aller dieser Listen – Komplexität = linear in der Größe der Liste viel kleiner als die Dokumentenmenge insgesamt! Ein einfacher Web-Server Eingabe – eine URL im Broswer, z.B. http://search.mpi-inf.mpg:8080/xyz – veranlasst dass eine Verbindung mit dem Rechner search.mpi-inf.mpg.de aufgebaut wird und folgende Zeichenkette an den Port 8080 geschickt wird (default ist Port 80) GET /xyz HTTP/1.1 Ausgabe – das Programm, dass auf search.mpi-inf.mpg.de läuft und auf Port 8080 lauscht, schickt etwas zurück – typischerweise eine HTML Datei – die dann im Browser angezeigt wird CompleteSearch Geschichte – entwickelt am Max-Planck-Institut für Informatik – über die letzten drei Jahre – unter meiner Leitung – mehrere Diplom- und Doktorarbeiten – zahlreiche Veröffentlichungen & Vorträge – voll einsatzfähige Suchmaschine Zahlreiche Demonstratoren – http://search.mpi-inf.mpg.de Anwendung 1: Autovervollständigung Nach jedem Tastendruck … – … zeige die besten Vervollständigungen des zuletzt eingegebenen Wortes, sowie die besten Treffer dafür – z.B., für die Suchanfrage user interface joy zeige joystick joysticks etc. und entsprechende Treffer Anwendung 2: Fehlerkorrektur Wie vorher, aber zeige zusätzlich … – … Varianten bez. Schreibweise der Vervollständigungen die zu einem Treffer führen – z.B. soll für die Suchanfrage probabilistic algorithm auch ein Dokument mit probalistic aigorithm als Treffer gelten Realisierung – angenommen, aigorithm kommt als Fehlschreibung von algorithm vor, dann für jedes Vorkommen von aigorithm im Index aigorithm Doc. 17 füge ebenso hinzu algorithm::aigorithm Doc. 17 Anwendung 3: Ähnliche Worte Wie vorher, aber zeige zusätzlich … – … Worte die sinngemäß dasselbe bedeuten wie ein der Vervollständigungen – z.B., für die Anfrage russia metal betrachte auch Dokumente mit russia aluminium Implementation – für beispielsweise jedes Vorkommen von aluminium im Index aluminium Doc. 17 füge hinzu (pro Vorkommen) s:67:aluminium Doc. 17 sowie (einmal für alle Dokumente) s:aluminium:67 Doc. 00 Anwendung 4: Facettensuche Wie vorher, aber zeige zusätzlich … – … eine Statistik bezüglich diverser Kategorien (wie oft welche Kategorie vorkommt) – z.B. für die Anfrage algorithm zeige (prominente) Autoren von Artikeln die dieses Wort enthalten Realisierung – z.B. für einen Artikel von Roswitha Bardohl, der in der Zeitschrift Theoretical Computer Science in 2007 erschienen ist, füge hinzu author:Roswitha_Bardohl venue:TCS year:2007 Dok. 17 Dok. 17 Dok. 17 – sowie auch (zur Vervollständigung von Kategoriennamen) roswitha:author:Roswitha_Bardohl bardohl:author:Roswitha_Bardohl etc. Dok. 17 Dok. 17 Anwendung 5: Semantische Suche Wie vorher, aber zeige zusätzlich … – … “semantische” Vervollständigungen – z.B. für die Suchanfrage audience pope politician zeige individuelle Politiker (nicht das Wort politician) die zusammen mit den Worten audience pope vorkommen Realisierung – man kann nicht einfach für jedes Vorkommen einer Entität alle Kategorien hinzufügen, zu denen diese Entität gehört, z.B. Angela Merkel ist politician, german, female, human being, organism, chancellor, adult, member of parliament, … – Lösung: trickreiche Kombination mit sogenannten “joins” und es gibt noch mehr Anwendungen … Formulierung des Kernproblems Daten gegeben als – Dokumente mit Worten – Dokumente haben Ids (D1, D2, …) – Worte haben Ids (A, B, C, …) Suchanfrage D74 D3 D17 D43 J W QD92 D1 Q D BW DQ AOE A U K AD53 D78P U D D27 WH EM J D E K L S D9 KLD D4 F D32 A D88 D98 D2 E E R K L KD13 B F AA B I L S P A EE B A GQ AOE DH S WH Treffer für “traffic” – sortierte Liste von Dok. Ids D13 D17 D88 … – Intervall von Wort Ids CDEFG Worte die mit “inter” beginnen Formulierung des Kernproblems Daten gegeben als – Dokumente mit Worten – Dokumente haben Ids (D1, D2, …) – Worte haben Ids (A, B, C, …) Suchanfrage D74 D3 D17 D43 J W QD92 D1 Q D BW DQ AOE A U K AD53 D78P U D D27 WH EM J D E K L S D9 KLD D4 F D32 A D88 D98 D2 E E R K L KD13 B F AA B I L S P A EE B A GQ AOE DH S WH Treffer für “traffic” – sortierte Liste von Dok. Ids D13 D17 D88 … – Intervall von Wort Ids CDEFG Worte die mit “inter” beginnen Antwort – alle passenden Wort-in-Dok. Paare D13 E D88 E D88 G … … – mit Scores 0.5 0.2 0.7 … “kontext-sensitive Präfixsuche” Lösung über invertierte Listen Zum Beispiel, traffic inter* gegeben die Dokumente: D13, D17, D88, … (Treffer für traffic) und der Wortbereich: CDEFG (Ids für inter*) Iteriere über alle Worte aus dem gegebenen Bereich C (interaction) D8, D23, D291, ... D (interesting) D24, D36, D165, ... E (interface) D13, D24, D88, ... F (interior) D56, D129, D251, ... G (internet) D3, D15, D88, ... typischerweise sehr viele Listen! Schneide jede Liste mit der gegebenen und vereinige alle Schnitte D13 E D88 E D88 G … … im worst case quadratische Komplexität Ziel: schneller ohne mehr Platz zu verbrauchen Einschub Die invertierten Listen sind, trotz quadratischer worstcase Komplexität, in der Praxis schwer zu schlagen – sehr einfacher Code Daten – Listen sehr gut komprimierbar – perfekte Zugriffslokalität Anzahl der Operationen ist ein trügerisches Maß – 100 disk seeks benötigen ca. eine halbe Sekunde – in der Zeit können 200 MB Daten gelesen werden (falls komprimiert gespeichert) – Hauptspeicher: 100 nichtlokale Zugriffe 10 KB am Stück Neu: Halb-Invertierte Listen Listen von Dokument-Wort Paaren (sortiert nach Dok. Id) A-D: 1 3 D A 3 C 5 A flache Partitionierung 5 B 6 A 7 C 8 8 9 11 11 11 12 13 15 A D A A B C A C A Alternative: hierarchisch – z.B. eine Liste für A-D, eine Liste für E-H, etc. Eigenschaften – einfach + perfekte Lokalität + sehr gut komprimierbar(!) Suchanfragen – bei geeigneter Partitionierung, immer genau eine Liste – extrem schnell: Ø 0.1 Sekunde / Anfrage für TREC Terabyte (426 GB Rohdaten, 25 Millionen Dokumente) Halb-Invertierte Listen: Komprimierung 1 3 D A 3 C 5 A 5 B 6 A 7 C 8 8 9 11 11 11 12 13 15 A D A A B C A C A Dok. Ids Differenzen und Wort Ids Häufigkeitsränge +1 + 2 +0 +2 +0 +1 +1 +1 + 0 +1 +2 +0 +0 +1 +1 + 2 3rd 1st 2nd 1st 4th 1st 2nd 1st 3rd 1st 1st 4th 2nd 1st 2nd 1st Kodiere alle Zahlen universell: x log2 x Bits +0 0 1st (A) 0 +1 10 2nd (C) 10 +2 110 3rd (D) 111 4th (B) 110 Was schließlich gespeichert wird 10 110 0 110 0 10 10 10 0 10 110 0 0 10 10 110 111 0 10 0 110 0 10 0 111 0 0 110 10 0 10 0 Ergebnis Platzverbrauch Definition – empirische Entropie einer Datenstruktur = optimale Anzahl Bits die zur Kodierung benötigt werden Theorem – empirische Entropie von HALB-INV mit Blockgröße ε∙n ist 1+ε mal die empirische Entropie von VOLL-INV Experimente (mit konkretem Kodierungsverfahren) HOMEOPATHY 44,015 Dok. 263,817 Worte mit Positionen WIKIPEDIA 2,866,503 Dok. 6,700,119 Worte mit Positionen TREC .GOV 25,204,013 Dok. 25,263,176 Worte ohne Positionen Orig.größe 452 MB 7.4 GB 426 GB VOLL-INV 13 MB 0.48 GB 4.6 GB HALB-INV 14 MB 0.51 GB 4.9 GB perfekte Übereinstimmung von Theorie und Praxis Zusammenfassung: CompleteSearch Output – Publikationen in verschiedenen Communities SIGIR (IR), CIDR (DB), SPIRE (Theory), GWEM (KI), … – zahlreiche öffentliche Installationen DBLP – Industriekontakte Entscheidend waren – Identifizierung und Formulierung des Präfixsuchproblems – Wahl der Analyseparameter: Lokalität, Komprimierung, etc. (und zum Beispiel hier nicht: Anzahl der Operationen) – generell: Wissen in vielen relevanten Gebieten