Transit Nodes für Matthias Westermann
Werbung
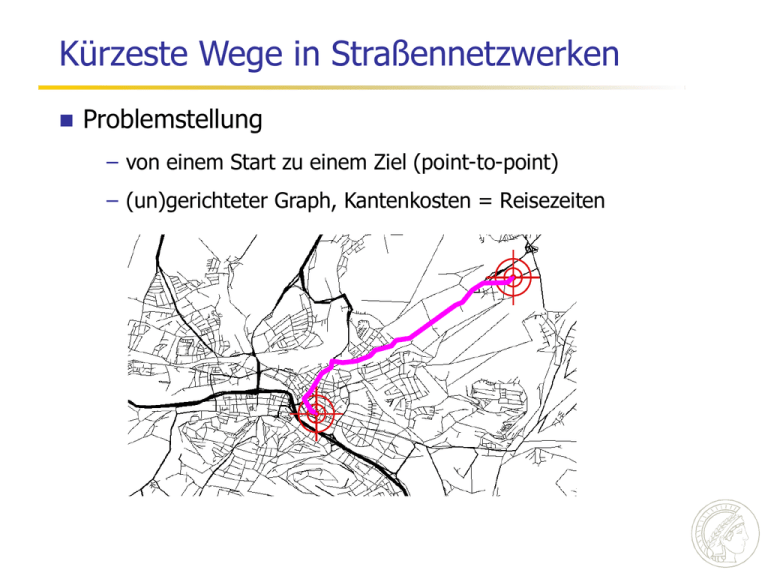
Kürzeste Wege in Straßennetzwerken Problemstellung – von einem Start zu einem Ziel (point-to-point) – (un)gerichteter Graph, Kantenkosten = Reisezeiten Stand der Kunst 24 Millionen Knoten 58 Millionen Kanten Dijkstra's Algorithmus ≈ 1 Sekunde pro Anfrage, USA Straßennetzwerk Für wesentlich schnellere Zeiten … muss das Netzwerk vorverarbeitet werden spezielle Eigenschaften von Straßennetzwerken Das bisher beste Verfahren ≈ 1 Millisekunde pro Anfrage, USA Netzwerk Unsere Arbeit zuerst: theoretisch sehr schöner Algorithmus Dijkstra '59 Luby and Ragde '85 ... Thorup and Zwick '01 Gutman '04 Goldberg et al '05/06 Sanders et al '04/05/06 Lauther et al '04 Möhring et al '05 Wagner et al '05/06 ... aber: konnten die 1 Millisekunde nicht schlagen dann radikal neuer Ansatz: Transitknoten ≈ 10 Mikrosekunden pro Anfrage, USA Straßennetzwerk Die Transitknoten Idee 1. Vorberechnung weniger Transitknoten mit der Eigenschaft, dass jeder kürzeste Pfad über eine gewisse Mindestdistanz durch einen Transitknoten geht 2. Vorberechnung der nächsten Transitknoten für jeden Knoten mit der Eigenschaft, dass jeder kürzeste Pfad über eine gewisse Mindestdistanz von diesem Knoten aus durch eine dieser nächsten Transitknoten geht 3. Vorberechnung aller Distanzen zwischen allen Paaren von Transitknoten und von jedem Knoten zu seinen nächsten Transitknoten Suchanfrage = wenige table lookups ! Vorberechnung der Transitknoten Von Distanzen zu Pfaden 2 Start 3 2 24 min 20 min 23 min Ziel Zusammenfassung: Kürzeste Wege Output – Publikationen: DIMACS’06, ALENEX’07, Science 07 – Großes Presseecho: Süddeutsche, Welt, c’t, Chip, … – Patent + zahlreiche Firmenkontakte + … – Heinz Billing Preis für wiss. Rechnen 2007 (mit S. Funke) – Scientific American 50 Award 2007 Charakteristik – Klassisches Problem, aber auf echten Daten – theoretisch schönerer Algorithmus war nicht praktikabel – einfache aber radikal neue Idee, enorme Verbesserung – Verständnis der Besonderheit der Daten entscheidend Ausblick: Kürzeste Wege Theoretische Untermauerung – wir haben schon: beweisbar korrekt – aber für genau welche Graphen: beweisbar effizient? Erweiterungen – dynamische Änderungen (Staus) – tageszeitabhängige Kantenkosten (rush hour) – Periodische Abfahrts/Ankunftszeiten (Bahn, Bus, etc.) – Erreichbarkeitsproblem auf Ontologiegraphen –…











