Ultrafast Shortest-Path Queries via Transit Nodes

Ultrafast Shortest-Path Queries via Transit Nodes
Nach Holger Bast, Stefan Funke, Domagoj Matijevic, Peter Sanders und Dominik Schultes
Seminar Algorithm Engineering – SoSe 2008
Ausarbeitung von Marius Heinzmann
1 Einleitung
Die klassische Lösung zur Berechnung kürzester Wege ist die Anwendung des Dijkstra Algorithmus,
der in O(m + n log m) Zeit selbigen findet, wobei m die Anzahl Kanten ist und n die Anzahl der
Knoten. Für die Berechnung zwischen zwei beliebigen Knoten im US-Straßennetzwerk, bestehend
aus ca. 24 Mio. Knoten und ca. 58 Mio. Kanten, dauert dies auf heutigen Rechnern mehr als
eine Sekunde. Für viele Anwendungen ist dies zu langsam. Obwohl es noch eine offene Frage ist, ob
Dijkstra [1] für solche Anfragen optimal ist, gibt es eine offensichtliche untere Schranke von Ω(m + n).
Um schnellere, sublineare, Anfragezeiten zu erreichen, muß eine Vorverarbeitung stattfinden. Holger
Bast et al. [2] stellten das Transitknoten-Konzept – ein allgemeines Konzept zur Auswahl einer Menge
an Straßenknoten für eine Vorberechnung – vor, auf welches im Folgenden näher eingegangen wird.
2 Transitknoten
Sei ein Straßennetzwerk G = (V , E ) gegeben, wobei V die Menge der Straßen-Knoten und E die
Menge der Straßenabschnitten ist. Das Ziel ist es kürzeste Distanzen vorauszuberechnen, so dass sich
Anfragen d(s, t) nach kürzesten Distanzen zwischen zwei Knoten s und t mittels der gespeicherten
Werte in sublinearer Zeit beantworten lassen. Allerdings kann man nicht einfach die kürzesten Distanzen zwischen allen Punktpaaren vorberechnen, da der Zeit- und Speicheraufwand für Graphen wie
das US-Straßennetzwerk unverhältnismäßig hoch ist. Also braucht es ein Kriterium, nach dem die
Punkte zur Vorberechnung ausgewählt werden. Bast et al. wählten die Menge der Transitknoten T
als Menge der Punkte für die Vorberechnung.
Diese basieren auf der Definition eines Lokalitätsfilters L : V × V 7→ {wahr, falsch}, der für zwei
gegebene Knoten entscheidet, ob diese so weit voneinander entfernt sind, dass der kürzeste Weg
zwischen ihnen über mindestens einen Transitknoten läuft.
Die Menge der Transitknoten T hat die Eigenschaft, dass jeder kürzeste Weg zwischen zwei Knoten
s, t mit ¬L(s, t) über mindestens einen Knoten aus T geht.
Weiterhin definieren Sie die Menge der Zugangsknoten A : V 7→ 2T zu einem Knoten v als die zu v
nächsten Transitknoten.
1
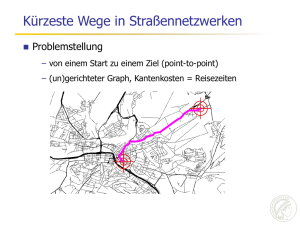
Abbildung 1 zeigt die Zugangsknoten für die Menge der Knoten aus dem schwarzen Quader im Zentrum
der Abbildung.
Angenommen es wäre ein Paar (L, T ) gegeben und L ist kompatibel mit T , d.h. es gibt kein
Knotenpaar u, v , so dass ¬L(u, v ) gilt und d(s, t) nicht über einen Knoten aus T läuft. Dann lässt
sich jede Anfrage d(s, t), für die ¬L(s, t) gilt wie folgt beantworten:
• Finde alle nächsten Zugangsknoten A(s) um s.
• Finde alle nächsten Zugangsknoten A(t) um t.
• Finde minv ∈A(s),u∈A(t) {d(s, v ) + d(v , u) + d(u, t)}.
Die Laufzeit der Vorausberechnung dieses Ansatzes wird davon dominiert, wie viele Transitknoten es
insgesamt, bzw. wie viele Zugangsknoten es für einen beliebigen Knoten gibt. Bast et al. stellten
fest, dass die Menge der Transitknoten für das US-Straßennetz ca. 10.000 Knoten umfasst und somit
relativ klein ist. Auch die Menge der Zugangsknoten ist mit 11 im Schnitt sehr klein. Dies erlaubt
es, die kürzesten Distanzen zwischen allen Transitknoten, sowie die kürzesten Distanzen zwischen
allen Knoten t ∈ V und ihren Zugangsknoten A(t) vorauszuberechnen. Kombiniert mit einer effektiven Definition des Lokalitätsfilters lässt sich damit jede solcher Anfragen mittels Tabellenanfragen
beantworten. Dies führt zu einer sehr deutlichen Steigerung gegenüber dem naiven Ansatz und einer
Verbesserung um den Faktor 50 gegenüber der Besten bisher bekannten Lösung.
Es gibt zwei Ansätze ein Paar (L, T ) zu ermitteln:
1. Man bestimmt T , oder sie sind bereits gegeben, und man definiert sich L so, dass er mit T
funktioniert.
2. Es wird zuerst L gewählt und anhand dessen T bestimmt.
Im Folgenden wird gemäß dem zweiten Ansatz verfahren, zuerst ein Lokalitätsfilter definiert und
anschließend anhand dessen die Transitknoten bestimmt.
3 Raster-Ansatz
Nachdem die allgemeine Vorgehensweise vorgestellt wurde, befasst sich dieser Abschnitt mit der Bestimmung der Transitknoten. Hierzu stellten Bast et al. einen Raster-basierten Ansatz vor. Dieser
unterteilt das Straßennetz in Zellen gleicher Größe, indem er ein gleichmäßiges r × r Raster, für ein
r ∈ N, über das Straßennetz legt. Darauf aufbauend definieren Sie den Lokalitätsfilter L(u, v ) =
(|C (u) − C (v )| <= 4) für zwei beliebige Knoten u, v ∈ V , wobei C (x) die Zelle ist, in der sich Knoten
x ∈ V befindet. Der Begriff Dijkstrasuche bezeichnet im Folgenden die Ausführung des von E. Dijkstra [1] entwickelten Algorithmus für die Suche nach kürzesten Pfaden zwischen einer Quelle und
einem Ziel. Anhand dieser Definitionen lässt sich ein naiver Ansatz zur Bestimmung der Transitknoten
definieren:
Es sei C eine beliebige Zelle und, wie in Abbildung 2 dargestellt, inner, ein Quadrat, das im Abstand
von 2 Zellen um C liegt, und outer, ein Quadrat, das mit 4 Zellen Abstand um C liegt. Nun bestimmt
man die Menge der Kanten die C schneiden und wählt zufällig für jede Kante einen Endpunkt aus, der
2
Figure 1: Zugangsknoten für Straßenknoten aus dem schwarzen Quader im Zentrum.
zur Menge VC hinzugefügt wird. Anschließend verfährt man analog mit Vinner und Vouter . Als nächstes
wird für jeden Punkt aus VC eine Dijkstrasuche gestartet, bis alle Knoten in Vouter gesetzt sind. Nun
wird der Transitknotentest durchgeführt. Dieser fügt die Knoten aus Vinner zu den Transitknoten TC
hinzugefügt, welche auf einem kürzesten Pfad von einem Knoten s ∈ VC zu einem Knoten t ∈ Vouter
liegen. Die Gesamtmenge der Transitknoten ist dann die Vereinigung der Transitknoten aller Zellen:
T = ∪i Ti .
Um die Berechnung von T effizienter zu gestalten, entwickelten Bast et al. einen Scanlinien-Ansatz
(siehe Abbildung 3). Bei diesem wird einmal entlang jeder Dimension gescannt und dabei in einem
Bereich B von zwei Zellen um die Scanlinie für jeden Punkt auf dieser eine Dijkstrasuche ausgeführt und anschließend ermittelt, ob dieser für die an B angrenzenden Zellen ein Transitknoten
ist. Für jeden Knoten v auf der Scanlinie sei Cl die Zellen links von v mit Abstand 2 und analog dazu Cr die Zellen rechts davon. Des weiteren seien Clv = {c ∈ Cl : dv (c, C (v )) ≤ 2}, bzw.
Crv = {c ∈ Cr : dv (c, C (v )) ≤ 2} der linke bzw. rechte Teilbereich zu einem Knoten v , wobei dv
dem vertikalen Abstand der gegebenen Zellen entspricht. Nun wird für jeden Knoten v auf der Scanlinie eine Dijkstrasuche ausgeführt bis die Knoten auf den Rändern von Clv und Crv gesetzt sind.
Anschließend führt man für jedes Randknoten-Paar a ∈ Cl , b ∈ Cr : dv (C (a), C (b)) ≤ 4 den Transitknotentest durch. D.h. es wird überprüft, ob einer der Knoten, die auf der Scanlinie liegen und die
innerhalb des vertikalen Bereichs von a und b sind, auf dem kürzesten Pfad zwischen a und b liegt.
Ist dies der Fall, so wird dieser als Transitknoten für C (b) und C (a) markiert.
Der Vorteil des Scanlinien-Ansatzes ist der geringere Radius der Dijkstrasuche – drei Zellen statt
fünf – und die damit einhergehende kürzere Laufzeit.
Sind alle Transitknoten bestimmt, so wird die Vorberechnung der kürzesten Distanzen zwischen
3
Figure 3: Scanlinien-Ansatz zur T -Berechnung.
Figure 2: Naiver Ansatz zur T -Berechnung.
allen Paaren von diesen ausgeführt und in Tabellenform abgelegt. Des weiteren wurde bereits bei
der Bestimmung der Transitknoten implizit die Berechnung der kürzesten Distanzen von einem beliebigen Knoten v zu dessen Zugangsknoten A(v ) vorgenommen, da die neu ermittelten Transitknoten
automatisch die Zugangsknoten für die beiden Endpunkte der zugehörigen Strecke sind. Aufgrund der
sich nur minimal unterscheidenden Mengen der Zugansknoten für räumlich nahe beieinanderliegende
Knoten, reicht es die Zugangsknoten pro Zelle zu speichern, d.h. es gilt: A(v ) = A(C (v )), ∀ v ∈ V .
Obgleich der Verbesserung durch den Scanlinienansatz muss weiterhin für alle Knoten auf der Scanlinie eine Dijkstrasuche ausgeführt werden. Um die Laufzeit weiter zu reduzieren ist eine Möglichkeit
den Transitknotentest nur noch für eine kleinere Menge an “potentiellen Transitknoten” durchgeführt.
4 Optimierungen
In diesem Abschnitt wird eine Methode vorgestellt, die die Anzahl der rechenaufwendige Dijkstrasuchen auf die Kardinalität der Menge “potentieller Transitknoten” reduziert.
Die zugrundeliegende Idee ist es, die Transitknoten für einen weiten Lokalitätsfilter aus der Menge
der Transitknoten für einen strikteren Lokalitätsfilter zu suchen. Auf den Gitteransatz übertragen
bedeutet dies, dass zuerst die Transitknoten für ein feineres Gitter an den Stellen bestimmt werden,
die sich mit dem gröberen Gitter überdecken. Anschließend werden aus dieser Menge der “potentiellen Transitknoten” die eigentlichen Transitknoten des gröberen Gitters gewählt, d.h. es wird bei
der Bestimmung der Transitknoten im gröberen Gitter nicht mehr für jeden Knoten auf der Scanlinie der Transitknotentest durchgeführt, sondern nur noch für die aus der Menge der “potentiellen
Transitknoten”. Diese Idee lässt sich leicht auf mehrere Ebenen erweitern.
Der Geschwindigkeitsvorteil durch die Einsparung an Dijkstrasuchen im gröberen Gitter scheint
den Mehraufwand aufgrund der erneuten Dijkstrasuchen für die Transitknoten im feineren Gitter zu
überwiegen. Die Autoren äußern sich leider nicht darüber, inwiefern dies einen Geschwindigkeitsvorteil
erbringt. Ebenso ist es noch eine offene Frage, ob durch diese Vorauswahl an Transitknoten im feinen
Gitter vielleicht auch Transitknoten des gröberen Gitters übersehen werden können.
4
Mit der abgeschlossenen Vorberechnung lassen sich nun Anfragen nach kürzesten Distanzen als auch
Anfragen nach kürzesten Pfaden beantworten.
5 Berechnung kürzester Wege
Da nur kürzeste Distanzen gespeichert werden, um wenig Speicher zu verbrauchen, reicht der bisherige
Ansatz nicht aus, um kürzeste Wege samt deren Kanten auszugeben.
Um dennoch den kürzesten Weg zwischen s und t ausgeben zu können, sucht man ausgehend von
s den Knoten u, so dass d(s, u) + d(u, t) = d(s, t). Anschließend führt man die Suche auf gleicher
Weise von u aus fort, bis man schließlich bei t angekommen ist. Sofern ¬L(u, t) gilt, lässt sich d(u, t)
mittels Transitknoten und den damit verbundenen Tabellenabfragen in annähernd konstanter Zeit
beantworten.
Dieser Ansatz lässt sich beschleunigen, indem man jede Kante im Transitknotengraphen mit dem
kürzesten Pfad zwischen den beiden Knoten assoziiert. Man nehme an, die beiden Zugansknoten, über
die der kürzeste Weg läuft seien x ∈ A(s) und y ∈ A(t). Die Ausgabe des kürzesten Weges zwischen
x und y ist dann in Zeit linear in der Anzahl der Kanten des korrespondierenden Pfades möglich.
Allerdings können lokale Anfragen nicht mittels Transitknoten berechnet werden und müssen daher
mit einem anderen Algorithmus zur Berechnung kürzester Pfade beantwortet werden.
6 Einführung mehrerer Gitterebenen
Lokale Anfragen brauchen, abhängig vom gewählten Suchalgorithmus, ein vielfaches der Zeit der globalen Anfragen. Der Anteil an globalen Anfragen lässt sich durch ein engmaschigeres Netz steigern.
Allerdings bedeutet dies eine größere Anzahl an Tranistknoten und damit auch eine längere Vorverarbeitungszeit bzw. einen dementsprechend größeren Platzbedarf. Um den Platzbedarf klein zu halten
und dennoch einen hohen Anteil an globalen Anfragen zu haben, kann man mehrere Ebenen an Transitknoten einführen.
Dazu führt man weitere Gitter und dazu korrespondierende Lokalitätsfilter ein. Diese seien vom
weitesten zum striktesten Filter geordnet, d.h. L1 entspricht dem Lokalitätsfilter für das gröbste Gitter
und Ln zu dem des feinsten Gitters. Nun berechnet man für das gröbste Gitter die Transitknoten
wie bisher. Anschließend bestimmt man die Transitknoten für das nächst feinere Gitter, allerdings
berechnet und speichert man nur die Distanzen zwischen Transitknoten t1 , t2 , die lokal in Bezug auf
das gröbere Gitter sind, d.h. für die L1 (t1 , t2 ) gilt. Dies ist nur für ein Bruchteil der Transitknoten
1
auf dieser Ebene nötig. Z.B. sind dies nur 200
der Transitknoten eines 256x256-Gitters für das USStraßennetz, wenn darüber ein 128x128-Gitter liegt. Es ist leicht zu sehen, dass sich beliebig viele
Ebenen auf diese Weise einführen lassen.
Zum Beantworten einer Anfrage werden nun in einem top-down Ansatz die Lokalitätsfilter abgefragt
und sobald einer davon fehlschlägt kann man die Transitknoten der korrespondierenden Ebene zur
Berechnung des kürzesten Weges heranziehen.
5
7 Diskussion
Holger Bast et al. führten mit den Transitknoten ein allgemeines Konzept zur Berechnung kürzester
Wege, in annähernd konstanter Zeit, mittels vorberechneten Distanzen ein. Basierend auf dem einfachen Gitteransatz ist dies eine speichereffiziente und äußerst schnelle Lösung, die besonders für
Verkehrssimulationen und Optimierungsprobleme in der Logistik interessant sein dürfte. Für den
Alltagsgebrauch ist diese Lösung ironischerweise zu schnell, denn bei Antwortzeiten im Bereich von
µs wird die Geschwindigkeit der Anwendung durch die bloße Anzeige des kürzesten Pfades mehr
beeinträchtigt als durch eine solche Anfrage.
References
[1] E. W. Dijkstra, “A note on two problems in connexion with graphs,” Numerische Mathematik,
vol. 1, pp. 269–271, 1959.
[2] H. Bast, S. Funke, D. Matijevic, P. Sanders, and D. Schultes, “In transit to constant
time shortest-path queries in road networks,” in ALENEX. SIAM, 2007. [Online]. Available:
http://www.siam.org/meetings/proceedings/2007/alenex/papers/transit.pdf
6