0 - Max Planck Institute for Informatics
Werbung

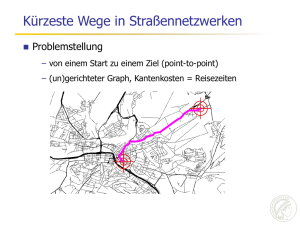
Intelligente Suche in sehr großen Datenmengen Vortrag an der Universität Mainz 5. März 2008 Holger Bast Max-Planck-Institut für Informatik Saarbrücken Früher: Klassische theoretische Informatik Komponenten – feststehende und voll spezifizierte Probleme zum Beispiel: gegeben ein Graph, berechne ein maximales Matching – vollständige Theoreme zum Beispiel: für einen zufälligen Graphen, maximales Matching in erwarteter Zeit O (n log n) – eventuell Experimente zum Beispiel: implementiere den Algorithmus und messe die Laufzeit auf vielen zufälligen Graphen Theorie als Selbstzweck – schult präzises Denken / Formulieren / Methodik – selten direkt relevant Hashing Sorting Scheduling Matching … Jetzt: Angewandt auf der Basis guter Theorie Komponenten – Ausgangspunkt ist eine reale Anwendung entscheidend diese in ihrer Ganzheit zu verstehen – Abstraktion kritischer Teile (theoretischem Denken zugänglich machen) oft der schwierigste und kreativste Teil – Algorithmen / Datenstrukturen entwerfen und mathem. analysieren wie in der klassischen Algorithmik, aber … – Experimente + Algorithm Engineering zur Ergänzung und Bestätigung der Theorie – Bau eines (Prototyp-) Systems ultimativer Realitätstest, wichtige Inspirationsquelle Theorie als Mittel zum Zweck – direkt anwendbare + verlässliche Lösungen – Anwendung geht vor mathematische Tiefe Überblick Meine Arbeitsweise – Früher: Klassische theoretische Informatik – Jetzt: Angewandt auf der Basis guter Theorie Ausgewählte Ergebnisse – Die CompleteSearch Suchmaschine ≈ 20 min – Spektrales Lernen ≈ 10 min – Kürzeste Wege in Straßennetzwerken ≈ 10 min Zusammenfassung – nach jedem Ergebnis Die CompleteSearch Suchmaschine Hintergrund – Suchmaschinen sind extrem schnell – auch für sehr großen Datenmengen – aber sie können nur genau eine Sache: Stichwortsuche Ziel – komplexere Suchfunktionen – aber genauso schnell Lösung – kontext-sensitive Präfixsuche – einerseits: sehr mächtig – andererseits: effizient berechenbar Mögliche Suchanfragen 1/2 Volltextsuche mit Autovervollständigung – traffic inter* Strukturierte Daten als künstliche Worte – venue:esa – author:elmar_schömer – year:2007 Elmar Schömer Michael Hemmer Laurent Dupont … ESA ESA ESA … 2007 2007 2007 … Datenbankanfragen: select, join, … – venue:esa author:* – venue:esa author:* und venue:sigir author:* und schneide die Menge der Vervollständigungen (an Stelle der Menge der Dokumente) paper #23876 paper #23876 paper #23876 … Mögliche Suchanfragen 2/2 Facettensuche – automatische Statistik über vordefinierte Kategorien Verwandte Worte – Suche metal, finde aluminium Fehlertolerante Suche – Suche probabilistic, finde probalistic Semantische Suche – Suche politician, finde Angela Merkel und mehr … alles mit ein- und demselben Mechanismus Formulierung des Kernproblems Daten gegeben als – Dokumente mit Worten – Dokumente haben Ids (D1, D2, …) – Worte haben Ids (A, B, C, …) Suchanfrage D74 D3 D17 D43 J W QD92 D1 Q D BW DQ AOE A U K AD53 D78P U D D27 WH EM J D E K L S D9 KLD D4 F D32 A D88 D98 D2 E E R K L KD13 B F AA B I L S P A EE B A GQ AOE DH S WH Treffer für “traffic” – sortierte Liste von Dok. Ids D13 D17 D88 … – Intervall von Wort Ids CDEFG Worte die mit “inter” beginnen Formulierung des Kernproblems Daten gegeben als – Dokumente mit Worten – Dokumente haben Ids (D1, D2, …) – Worte haben Ids (A, B, C, …) Suchanfrage D74 D3 D17 D43 J W QD92 D1 Q D BW DQ AOE A U K AD53 D78P U D D27 WH EM J D E K L S D9 KLD D4 F D32 A D88 D98 D2 E E R K L KD13 B F AA B I L S P A EE B A GQ AOE DH S WH Treffer für “traffic” – sortierte Liste von Dok. Ids D13 D17 D88 … – Intervall von Wort Ids CDEFG Worte die mit “inter” beginnen Antwort – alle passenden Wort-in-Dok. Paare D13 E D88 E D88 G … … – mit Scores 0.5 0.2 0.7 … Kontext-sensitive Präfixsuche Lösung via Invertierter Index (INV) Zum Beispiel, traffic inter* gegeben die Dokumente: D13, D17, D88, … (Treffer für traffic) und der Wortbereich: CDEFG (Ids für inter*) Iteriere über alle Worte aus dem gegebenen Bereich C (interaction) D8, D23, D291, ... D (interesting) D24, D36, D165, ... E (interface) D13, D24, D88, ... F (interior) D56, D129, D251, ... G (internet) D3, D15, D88, ... typischerweise sehr viele Listen! Schneide jede Liste mit der gegebenen und vereinige alle Schnitte D13 E D88 E D88 G … … im worst case quadratische Komplexität Ziel: schneller ohne mehr Platz zu verbrauchen Grundlegende Idee Berechne invertierte Listen für Bereiche von Worten Liste für A-D 1 3 D A 3 C 5 A 5 B 6 A 7 C 8 8 9 11 11 11 12 13 15 A D A A B C A C A Beobachtungen – ein Präfix entspricht einem Bereich von Worten – idealerweise Liste für jeden Präfix vorberechnet – aber das kostet viel zu viel Platz – erhebliche Redundanz zwischen den Listen Lösung 2: AutoTree Baumartige Anordnung Theorem: 1 1 1 1 1 1 1 1 1 1 … – Verarbeitungszeit O(|D| + |output|) (ausgabesensitiv) – ohne mehr Platz zu verbrauchen als INV Aber 1 0 0 0 1 0 0 1 1 1 … 1 0 0 1 1 … – nicht IO-effizient (wegen Bitvektor Operationen) – suboptimale Kompression Lösung 2: AutoTree SPIRE’06 / JIR’07 Trick 1: Relative bit vectors – the i-th bit of the root node corresponds to the i-th doc – the i-th bit of any other node corresponds to the i-th set bit of its parent node aachen-zyskowski 1111111111111… corresponds to doc 5 maakeb-zyskowski 1001000111101… corresponds to doc 5 maakeb-stream 1001110… corresponds to doc 10 Lösung 2: AutoTree SPIRE’06 / JIR’07 Tricks 2: Push up the words – For each node, by each set bit, store the leftmost word of that doc that is not already stored by a parent node D = 5, 7, 10 W = max* D = 5, 10 (→ 2, 5) report: maximum 1 1 1 1 1 1 1 1 1 1 … 1 0 0 0 1 0 0 1 1 1 … D=5 report: Ø → STOP 1 0 0 1 1 … Lösung 2: AutoTree SPIRE’06 / JIR’07 Tricks 3: divide into blocks – and build a tree over each block as shown before Lösung 2: AutoTree SPIRE’06 / JIR’07 Tricks 3: divide into blocks – and build a tree over each block as shown before Solution 2: AutoTree SPIRE’06 / JIR’07 Tricks 3: divide into blocks – and build a tree over each block as shown before Theorem: – query processing time O(|D| + |output|) – uses no more space than an inverted index AutoTree Summary: + output-sensitive – not IO-efficient (heavy use of bit-rank operations) – compression not optimal Einschub Der invertierte Index ist, trotz quadratischer worst-case Komplexität, in der Praxis schwer zu schlagen – sehr einfacher Code Daten – Listen sehr gut komprimierbar – perfekte Zugriffslokalität schlechte Lokalität Anzahl der Operationen ist ein trügerisches Maß – 100 disk seeks benötigen ca. eine halbe Sekunde – in der Zeit können 200 MB Daten gelesen werden (falls komprimiert gespeichert) – Hauptspeicher: 100 nichtlokale Zugriffe 10 KB am Stück Lokalität + Kompression entscheidend bei sehr großen Datenmengen Lösung 3: Hybrider Index (HYB) Flache Aufteilung des Vokabulars in Blöcke Liste für A-D 1 3 D A 3 C 5 A 5 B 6 A 7 C 8 8 9 11 11 11 12 13 15 A D A A B C A C A Liste für E-J 2 E 2 F 3 G 3 J 4 H 4 I 7 I 7 E Liste für K-N 1 L 1 2 3 4 N M N N 5 K 6 6 6 8 9 L M N M K 8 F 8 9 G H 9 11 J I 9 9 10 10 L M K L Gute Lokalität, aber was ist mit Kompression? Lösung 3: Hybrider Index (HYB) Flache Aufteilung des Vokabulars in Blöcke 1 3 D A 3 C 5 A 5 B 6 A 7 C 8 8 9 11 11 11 12 13 15 A D A A B C A C A Dok. Ids Differenzen und Wort Ids Häufigkeitsränge +1 + 2 +0 +2 +0 +1 +1 +1 + 0 +1 +2 +0 +0 +1 +1 + 2 3rd 1st 2nd 1st 4th 1st 2nd 1st 3rd 1st 1st 4th 2nd 1st 2nd 1st Kodiere alle Zahlen universell: x log2 x Bits +0 0 1st (A) 0 +1 10 2nd (C) 10 +2 110 3rd (D) 111 4th (B) 110 Was schließlich gespeichert wird 10 110 0 110 0 10 10 10 0 10 110 0 0 10 10 110 111 0 10 0 110 0 10 0 111 0 0 110 10 0 10 0 Definition: Empirische Entropie Empirische Entropie – … formalisiert die optimale Anzahl Bits die zur Kodierung einer Sequenz benötigt werden – … für eine Multi-Teilmenge der Größe m aus einem Universum der Größe n m ∙ log (1 + n / m) + n ∙ log (1 + m / n) – … für eine Folge von n Elementen aus einem Universum der Größe k, mit ni Vorkommen des i-ten Elements n1 ∙ log (n / n1) + ∙∙∙ + nk ∙ log (n / nk) – usw … Platzverbrauch: INV gegen HYB Theorem: Die empirische Entropie des INV Index ist Σ ni ∙ (1/ln 2 + log2(n/ni)) Theorem: Die empirische Entropie des HYB Index ist Σ ni ∙ ((1+ε)/ln 2 + log2(n/ni)) ni = number of documents containing i-th word, n = number of documents, ε = 0.1 MEDBOOKS WIKIPEDIA TREC .GOV Orig.größe 452 MB 7.4 GB 426 GB VOLL-INV 13 MB 0.48 GB 4.6 GB HALB-INV 14 MB 0.51 GB 4.9 GB 44,015 Dok. 263,817 Worte mit Positionen 2,866,503 Dok. 6,700,119 Worte mit Positionen 25,204,013 Dok. 25,263,176 Worte ohne Positionen perfekte Übereinstimmung Theorieals und Praxis … und HYB etwa 10 malvon schneller INV Zusammenfassung: CompleteSearch Output – Publikationen in verschiedenen Communities SIGIR (IR), CIDR (DB), SPIRE (Theorie), GWEM (KI), … – zahlreiche Industriekontakte, Vortrag bei Google – zahlreiche Installationen, auch kommerzielle DBLP – DFG Projekt im SPP Algorithm Engineering – Dr. Meyer Struckmann Wissenschaftspreis 2007 (15.000 €) Entscheidend waren – Identifizierung und Formulierung des Präfixsuchproblems – Wahl der Analyseparameter: Lokalität, Komprimierung, etc. (und zum Beispiel hier nicht: Anzahl der Operationen) – Experimente, Software Engineering, Prototyp – generell: Wissen in vielen relevanten Gebieten (z.B. Ontologien) Ausblick: Suche Sehr viele theoretisch interessante + praktisch relevante Probleme im Rahmen von Suche – effiziente(re) Facettensuche, semantische Suche, etc. – fehlertolerante Suche – Indexkonstruktion – effiziente Erzeugung von „result snippets” –… Übertragung auf Nicht-Text Retrieval – 3D shape retrieval – Suche in Bildern und Videos –… Überblick Meine Arbeitsweise – Früher: Klassische theoretische Informatik – Jetzt: Angewandt auf der Basis guter Theorie Ausgewählte Ergebnisse – Die CompleteSearch Suchmaschine ≈ 20 min – Spektrales Lernen ≈ 10 min – Kürzeste Wege in Straßennetzwerken ≈ 10 min Zusammenfassung – nach jedem Ergebnis Spektrales Lernen Daten als Objekt-Feature Matrix gegeben – Bilder, Formen, Text, … – z.B. Objekte = Dokumente, Features = Worte internet web surfing beach 1 1 1 0 0 1 1 0 1 0 1 0 0 0 1 1 Problem: fehlende Einträge 0 0 0 1 Spektrales Lernen Daten als Objekt-Feature Matrix gegeben – Bilder, Formen, Text, … – z.B. Objekte = Dokumente, Features = Worte internet web surfing beach 1 1 1 0 0 1 1 0 1 0 1 0 0 0 1 1 Problem: fehlende Einträge 0 0 0 1 0.8 0.8 1.2 -0.1 0.6 0.6 0.9 0.0 0.6 0.6 0.9 0.0 0.1 0.1 0.8 1.1 -0.2 -0.2 0.3 0.9 Lösung: Rang-k Approximation (durch Eigenvektorzerlegung) die Approximation erhöht die Präzision Wann und warum funktioniert das? Vorgängerarbeiten: Wenn die Objekte durch Kombination von k Basisobjekten generiert und leicht perturbiert werden, dann funktioniert die Rang-k Approximation – Papadimitriou, Tamaki, Raghavan, Vempala PODS 1998 – Ding SIGIR 1999 – Thomas Hofmann Machine Learning 2000 – Azar, Fiat, Karlin, McSherry, Saia STOC 2001 – und viele andere mehr … Mathematisch interessant (Perturbationstheorie) aber … – in der Regel gibt es keine k natürlichen Basisobjekte – Verbesserung durch Approximation ist extrem intransparent Alternative Sicht Betrachte die Feature-Feature Korrelations-Matrix (Objekt-Objekt Korrelations-Matrix ginge genauso gut) internet 0.8 0.1 0.6 0.1 0.3 0.4 0.3 -0.1 web 0.1 1.1 0.9 0.1 0.4 0.4 0.3 -0.2 surfing 0.6 0.9 1.1 0.7 0.3 0.3 0.4 0.3 beach 0.1 0.1 0.7 2.0 -0.1 -0.2 0.3 0.8 paarweise Skalarprodukte der norm. Zeilen-Vektoren beste Rang-2 Approximation Alternative Sicht Betrachte die Feature-Feature Korrelations-Matrix (Objekt-Objekt Korrelations-Matrix ginge genauso gut) internet 0.8 0.1 0.6 0.1 0.9 -0.1 0.2 -0.1 web 0.1 1.1 0.9 0.1 -0.1 0.8 0.3 -0.2 surfing 0.6 0.9 1.1 0.7 0.2 0.3 0.4 0.3 beach 0.1 0.1 0.7 2.0 -0.1 -0.2 0.3 0.8 paarweise Skalarprodukte der norm. Zeilen-Vektoren beste Rang-3 Approximation die approximierten Korrelationen hängen stark vom Rang ab! Zentrale Beobachtung Korrelation Abhängigkeit der Korrelation eines festen Paares vom Rang k der Approximation logic / logics 0 node / vertex 0 200 400 600 Rang der Approximation logic / vertex 0 200 400 600 Rang der Approximation 0 200 400 600 Rang der Approximation kein einzelner Rang ist gut für alle Paare! Zentrale Beobachtung Korrelation Abhängigkeit der Korrelation eines festen Paares vom Rang k der Approximation logic / logics 0 node / vertex 0 200 400 600 Rang der Approximation logic / vertex 0 200 400 600 Rang der Approximation 0 200 400 600 Rang der Approximation kein einzelner Rang ist gut für alle Paare! aber die Form der Kurve scheint ein guter Indikator zu sein Kurven für verwandte Terme Wir nennen zwei Terme perfekt verwandt wenn sie mit exakt den gleichen Termen vorkommen Korrelation beweisbare Form im idealisierten Fall · · · · · 1 1 0 0 · · · · · 0 0 1 1 · · · · · 1 1 1 1 0 0 1 1 1 1 0 1 0 Term 1 0 0 1 1 1 0 1 0 1 Term 2 beweisbar kleine Änderung auf halbem Wege nach kleiner Perturbation zu einer realen Matrix 0 0 200 400 600 Rang der Approximation Die Stelle des Abfalls ist für jedes Term-Paar anders! 0 200 400 600 Rang der Approximation 0 200 400 600 Rang der Approximation Charakteristische Form: hoch und wieder runter Kurven für nicht-verwandte Terme Ko-Okkurrenz Graph: – Knoten = Terme – Kanten = zwei Terme kommen zusammen vor perfekt unverwandt = kein Pfad Korrelation beweisbare Form im idealisierten Fall beweisbar kleine Änderung nach kleiner Perturbation auf halbem Wege zu einer realen Matrix 0 0 200 400 600 Rang der Approximation 0 200 400 600 Rang der Approximation 0 200 400 600 Rang der Approximation Charakteristische Form: Oszillation um Null Ein einfacher Algorithmus Normalisiere die Term-Dokument Matrix, so dass der theoretische Abfallpunkt für alle Termpaare gleich ist 2. Für jedes Termpaar: falls die Kurve je negativ ist vor diesem Punkt, setze Korrelation auf 1, sonst auf 0 Korrelation 1. 0 setze auf 1 0 200 400 setze auf 1 600 Rang der Approximation 0 200 400 setze auf 0 600 Rang der Approximation 0 200 400 600 Rang der Approximation einfache 0-1 Klassifikation, keine fraktionalen Einträge Zusammenfassung: Spektrales Lernen Ergebnisse – Einsicht: Spektrale Lernverfahren funktionieren, indem sie Paare von verwandten Features (Terme) identifizieren – Integration mit CompleteSearch (inspirierte weitere Forschung) – dadurch erstmalig transparent – „magisches” Verfahren entzaubert durch Theorie + Empirik From: Prabhakar Raghavan <[email protected]> Date: [after my SIGIR’05 talk] Subject: Very clear talk Thank you – it’s too easy to make this stuff mystical and you did the opposite Ausblick: Maschinelles Lernen Spektralzerlegung in diesem Fall nicht praktikabel – hoher Berechnungsaufwand (Spektralzerlegung) – relativ geringer Nutzen (findet verwandte Paare) Effizientes Maschinelles Lernen – Entitätenerkennung auf sehr großen Datenmengen – Fehlerkorrektur auf sehr großen Datenmengen –… Überblick Meine Arbeitsweise – Früher: Klassische theoretische Informatik – Jetzt: Angewandt auf der Basis guter Theorie Ausgewählte Ergebnisse – Die CompleteSearch Suchmaschine ≈ 20 min – Spektrales Lernen ≈ 10 min – Kürzeste Wege in Straßennetzwerken ≈ 10 min Zusammenfassung – nach jedem Ergebnis Kürzeste Wege in Straßennetzwerken Problemstellung – von einem Start zu einem Ziel (point-to-point) – (un)gerichteter Graph, Kantenkosten = Reisezeiten Stand der Kunst 24 Millionen Knoten 58 Millionen Kanten Dijkstra's Algorithmus ≈ 1 Sekunde pro Anfrage, USA Straßennetzwerk Für wesentlich schnellere Zeiten … muss das Netzwerk vorverarbeitet werden spezielle Eigenschaften von Straßennetzwerken Das bisher beste Verfahren ≈ 1 Millisekunde pro Anfrage, USA Netzwerk Unsere Arbeit zuerst: theoretisch sehr schöner Algorithmus Dijkstra '59 Luby and Ragde '85 ... Thorup and Zwick '01 Gutman '04 Goldberg et al '05/06 Sanders et al '04/05/06 Lauther et al '04 Möhring et al '05 Wagner et al '05/06 ... aber: konnten die 1 Millisekunde nicht schlagen dann radikal neuer Ansatz: Transitknoten ≈ 10 Mikrosekunden pro Anfrage, USA Straßennetzwerk Die Transitknoten Idee 1. Vorberechnung weniger Transitknoten mit der Eigenschaft, dass jeder kürzeste Pfad über eine gewisse Mindestdistanz durch einen Transitknoten geht 2. Vorberechnung der nächsten Transitknoten für jeden Knoten mit der Eigenschaft, dass jeder kürzeste Pfad über eine gewisse Mindestdistanz von diesem Knoten aus durch eine dieser nächsten Transitknoten geht 3. Vorberechnung aller Distanzen zwischen allen Paaren von Transitknoten und von jedem Knoten zu seinen nächsten Transitknoten Suchanfrage = wenige table lookups ! Vorberechnung der Transitknoten Von Distanzen zu Pfaden 2 Start 3 2 24 min 20 min 23 min Ziel Zusammenfassung: Kürzeste Wege Output – Publikationen: DIMACS’06, ALENEX’07, Science 07 – Großes Presseecho: Süddeutsche, Welt, c’t, Chip, … – Patent + zahlreiche Firmenkontakte + … – Heinz Billing Preis für wiss. Rechnen 2007 (mit S. Funke) – Scientific American 50 Award 2007 Charakteristik – Klassisches Problem, aber auf echten Daten – theoretisch schönerer Algorithmus war nicht praktikabel – einfache aber radikal neue Idee, enorme Verbesserung – Verständnis der Besonderheit der Daten entscheidend Ausblick: Kürzeste Wege Theoretische Untermauerung – wir haben schon: beweisbar korrekt – aber für genau welche Graphen: beweisbar effizient? Erweiterungen – dynamische Änderungen (Staus) – tageszeitabhängige Kantenkosten (rush hour) – Periodische Abfahrts/Ankunftszeiten (Bahn, Bus, etc.) –…