Atom- und Molekülphysik - AGeS - Die Skript

Atom- und Molekülphysik
nach den Vorlesungen von Prof. Dr. Lukas M. Eng
(Sommersemester 2008)
Herausgegeben von
Jeffrey Kelling
Felix Lemke
Stefan Majewsky
Stand: 23. Oktober 2008
Inhaltsverzeichnis
Vorwort (zuerst lesen)
1 Allgemeines
1.1 Aufgaben der Atom- und Molekülphysik .
1.2 Experimentelle Methoden . . . . . . . . .
1.2.1 Imaging . . . . . . . . . . . . . . .
1.2.2 Spektroskopie . . . . . . . . . . . .
1.3 Entwicklung und Historie der Atomphysik
4
.
.
.
.
.
5
5
5
5
6
6
2 Klassische Ansätze
2.1 Das Rutherford-Bohr’sche Atommodell . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.2 Spektralserien und Energieniveauschema des H-Atoms . . . . . . . . . . . . . . . . . .
8
8
10
3 Quantenmechanik
3.1 Die zeitabhängige Schrödingergleichung . . .
3.2 Die stationäre Schrödingergleichung . . . . . .
3.3 Die Schrödingergleichung im Nullpotential . .
3.4 Die Schrödingergleichung im Zentralpotential
3.5 Die Grobstruktur des H-Atoms . . . . . . . .
.
.
.
.
.
13
13
14
15
15
19
.
.
.
.
.
20
20
23
24
24
25
.
.
.
.
.
.
.
.
.
.
28
28
30
31
32
34
34
35
36
37
40
6 Atomstrukturen mit mehreren Elektronen
6.1 Die elektrostatische Korrelation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
6.2 LS-Kopplung und jj-Kopplung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
44
44
44
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
4 Fein- und Hyperfeinstruktur des H-Atoms
4.1 „Normale“ Feinstrukturaufspaltung (Spin-Bahn-Kopplung)
4.1.1 Relativistische Korrekturen . . . . . . . . . . . . .
4.1.2 Korrekturen für die endliche Ladungsdichte . . . .
4.2 Lamb-Shift. Anomale Feinstrukturverschiebung . . . . . .
4.3 Hyperfeinstruktur und Isotopieeffekt . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
5 Verallgemeinerung der Quantenmechanik
5.1 Operatoren. Eigenwerte. Eigenfunktionen. Quantenmechanischer Mittelwert
5.2 Dirac-Schreibweise und Matrixdarstellung . . . . . . . . . . . . . . . . . . .
5.3 Postulate der Quantenmechanik . . . . . . . . . . . . . . . . . . . . . . . . .
5.4 Der quantenmechanische Oszillator . . . . . . . . . . . . . . . . . . . . . . .
5.5 Der Potentialtopf . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5.5.1 Unbegrenzter quadratischer Potentialtopf . . . . . . . . . . . . . . .
5.5.2 Begrenzter, quadratischer Potentialtopf . . . . . . . . . . . . . . . .
5.5.3 Quantenmechanischer Tunneleffekt . . . . . . . . . . . . . . . . . . .
5.6 Auswahlregeln und Übergangsmatrixelemente . . . . . . . . . . . . . . . . .
5.7 Zweiniveausysteme. Einstein-Koeffizienten. Laser . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
6.3
6.4
6.5
Pauli-Prinzip. Symmetrie von Wellenfunktionen . . . . . . .
Die Struktur des He-Atoms . . . . . . . . . . . . . . . . . .
Aufbauprinzip. Periodensystem der Atome . . . . . . . . . .
6.5.1 Ionisationsenergien der Atome . . . . . . . . . . . . .
6.6 Spektrum der Alkali-Atome . . . . . . . . . . . . . . . . . .
6.7 Spektrum der Erdalkali-Atome und Zweielektronen-Systeme
6.8 Multiplett-Spektrum der Mehrelektronensystem . . . . . . .
6.9 Energiestruktur von Ionen . . . . . . . . . . . . . . . . . . .
6.10 Energiestruktur der inneren Elektronenschalen . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
45
47
51
52
53
54
54
55
56
7 Atome in äußeren Feldern
7.1 Zeeman-Effekt . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7.1.1 Normaler Zeeman-Effekt. Lorentz-Tripletts . . . . . . . . . . . . .
7.1.2 Anomaler Zeeman-Effekt . . . . . . . . . . . . . . . . . . . . . . . .
7.1.3 Quadratischer Zeeman-Effekt: Diamagnetismus und Landaubereich
7.1.4 Zusammenfassung . . . . . . . . . . . . . . . . . . . . . . . . . . .
7.2 Stark-Effekt . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7.2.1 Erste Ordnung der Störungsrechnung . . . . . . . . . . . . . . . . .
7.2.2 Zweite Ordnung der Störungsrechnung . . . . . . . . . . . . . . . .
7.2.3 Starkeffekt für Zustände n > 1 . . . . . . . . . . . . . . . . . . . .
7.2.4 Parabolische Koordinaten . . . . . . . . . . . . . . . . . . . . . . .
7.2.5 Elektrische Feldionisation. Quantenmechanischer Tunneleffekt . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
57
57
57
58
61
62
62
63
63
64
65
65
8 Molekülphysik
8.1 Allgemeine Bemerkungen . . . . . . . . . . . . .
8.1.1 Definitionen . . . . . . . . . . . . . . . . .
8.1.2 Aufgaben der Molekülphysik . . . . . . .
8.1.3 Darstellung von Molekülen . . . . . . . .
8.1.4 Analytik . . . . . . . . . . . . . . . . . . .
8.2 Bindungstypen . . . . . . . . . . . . . . . . . . .
8.3 Modellvorstellungen . . . . . . . . . . . . . . . .
8.3.1 Kossel-Modell . . . . . . . . . . . . . . . .
8.3.2 Lewis-Modell . . . . . . . . . . . . . . . .
8.3.3 Quantenmechanische Modellvorstellung .
8.4 Einige spezielle Bindungen . . . . . . . . . . . . .
8.4.1 π- und σ-Bindungen . . . . . . . . . . . .
8.4.2 Hybridisierung . . . . . . . . . . . . . . .
8.5 Mehrfachbindungen. Mesomerie . . . . . . . . . .
8.6 Bindungsverhältnisse in Festkörpern . . . . . . .
8.7 Rotations- und Schwingungsniveaus in Molekülen
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
67
67
67
67
67
68
68
69
69
69
70
73
73
74
76
77
77
Stichwortverzeichnis
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
82
Vorwort
Bevor Ihr beginnt, mit diesem Skript zu arbeiten, möchten wir Euch darauf hinweisen, dass dieses
Skript weder den Besuch der Vorlesung noch das selbstständige Nacharbeiten des Stoffes ersetzt. Wer
das nicht verstanden hat, bei dem kann die Benutzung des Skriptes für Probleme insbesondere im
Verständnis des Stoffes sorgen.
Das liegt daran, dass das Skript nicht als vorgekauter Wissensspeicher zu verstehen ist. Das hier ist eine
Abschrift des Inhaltes, den die Vorlesung zu vermitteln versucht. Nicht enthalten sind zum Beispiel
mündliche Kommentare des Professoren, auch wenn diese im individuellen Falle oft erst den Groschen
fallen lassen.
Gut geeignet ist das Skript einfach gesagt als Wissensstütze, also zum Beispiel zum schnellen Nachschlagen; außerdem zum Wiederholen früheren Stoffes, sofern ein ausreichendes Grundverständnis vorhanden ist. Nach diesen einleitenden Worten wünschen wir Euch viel Spaß bei der Arbeit mit diesem
Skript und viel Erfolg beim Studium!
Die AGeS-Redaktion
www.ages-skripte.org
P.S. Wir suchen immer Helfer, die unsere Skripte um neue Inhalte erweitern, Fehler suchen, oder das
Layout ansprechender gestalten wollen. Wenn Ihr Lust habt, meldet Euch über unsere Webseite.
1.2 Experimentelle Methoden
Seite 5
1 Allgemeines
1.1 Aufgaben der Atom- und Molekülphysik
Die Atom- und Molekülphysik untersucht die physikalischen und chemischen Eigenschaften von Atomen
und Molekülen sowie daraus resultierende optische, mechanische und elektronische Auswirkungen.
Weiterhin sollen, wie in der Experimentalphysik, dazu nutzbare Methoden entwickelt, angewandt und
diskutiert werden.
Im Rahmen dieser Vorlesung werden die Erkenntnisse aus anderen Teilen der Physik, zum Beispiel der
Quantenmechanik, genutzt, um die Eigenschaften einzelner Atome beschreiben zu können. Indem man
untersucht, wie Atome sich unter Einfluss äußerer elektromagnetischer Felder verhalten, kann man zur
Beschreibung von ganzen Molekülen gelangen.
1.2 Experimentelle Methoden
• Imaging – Abbildung von Atomen und Molekülen auf atomarer Skala
• Spektroskopie – Variation von Parametern einer äußeren Einwirkung (zum Beispiel Wellenlänge
bei elektromagnetischen Wellen)
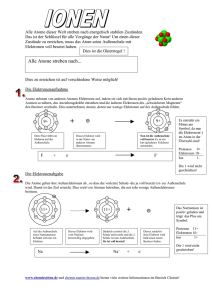
1.2.1 Imaging
Zur Untersuchung von Kristallen wird ein Feldionenmikroskop verwendet. In diesem ist eine Probe von einem mit einem Fluroeszenzfarbstoff
beschichteten Schirm umgeben. Über eine kleine Öffnung, ein sogenanntes Inlet, werden Heliumatome eingelassen. Zwischen Schirm und Probe
liegt eine Spannung an, sodass die Heliumatome bei Kontakt mit der Probe ionisiert und zum Schirm hin beschleunigt werden. Beim Auftreffen
auf die Fluoreszenzschicht entsteht ein sichtbarer Leuchtpunkt, dessen
Position Aussagen über die Struktur der Probe ermöglicht.
Prinzipskizze zum Feldionenmikroskop
Mit einen solchem Gerät lässt sich nur die Oberflächenstruktur der Probe untersuchen, nicht jedoch
das sogenannte Bulk, das Innere des Festkörpers, welches konstante physikalische Eigenschaften aufweist.
1.3 Entwicklung und Historie der Atomphysik
Seite 6
Beim Transmissionselektronenmikroskop (TEM) strahlt ein monochromatischer Elektronenstrahl durch eine Probe hindurch, wobei es zu Interferenz- und
Beugungserscheinungen kommt. Über eine Fouriertransformation erhält man
hieraus ein direktes Bild der Probe.
Man erhält jedoch nur eine zweidimensionale Projektion der Probe. Nachteilig
ist außerdem, dass die Messung in einem Hochvakuum stattfinden muss, um
Streueffekte am Elektronenstrahl zu vermeiden und die Probe speziell präpariert
werden muss, da die Schichtdicke maximal 10 nm betragen darf.
Eine dritte Möglichkeit ist die Verwendung eines Rastersondenmikroskops.
Hier ist insbesondere das Rastertunnelmikroskop (scanning tunneling microscope, STM) zu nennen, welches auch Kräfte und optische Eigenschaften in
atomaren Strukturen abbilden kann.
Aufbau eines TEM
1.2.2 Spektroskopie
Schickt man zum Beispiel eine elektromagnetische Welle oder einen Teilchenstrom auf eine Probe, so werden Teile des Stromes gestreut, absorPrinzip der Spektroskopie
biert, reflektiert und transmittiert. Diese Anteile
können durch Analysatoren qualitativ untersucht
und mittels Detektoren quantifiziert werden. Um verlässliche Ergebnisse zu erhalten, muss man monochromatische Energieströme einsetzen (bei Licht nur eine Wellenlänge, bei Teilchen nur eine kinetische
Energie für alle Teilchen).
Durch das Spektroskopieren kann man zum Beispiel Informationen über atomare oder molekulare
Abstände, Austrittarbeiten, Zustandsdichten oder die Spineinstellung eines Systems erhalten. Im
Gegensatz zum Imaging findet die Spektroskopie nicht im ~r-Raum statt, sondern im ~k-Raum. Das
heißt, es wird nicht ein direktes Bild geliefert, sondern die Fouriertransformation dieses Bildes.
In diesem Zusammenhang ist das Babinet-Prinzip von besonderer Relevanz: Von der Beugung am
Streuer kann man zur Beugung an der entsprechenden Apertur übergehen, denn das Beugungsbild
zweier geometrisch komplementärer Blenden ist identisch.
1.3 Entwicklung und Historie der Atomphysik
Um 500 v. Chr. stellten sich Philosophen wie Demokrit die Materie als aus unteilbaren (gr. atomos)
Teilen zusammengesetzt vor. Im 12. Jh. fanden indische Philosophen weitere indirekte Indizien für
diese These.
In der Physik wurde dieses Problem mit dem Aufkommen der Newtonschen Axiome im 18. Jh.
diskutierbar. Dalton nutzte die Idee der Atome, um 1808 das erste Periodensystem der Elemente
aufzustellen. Zum Ende des 19. Jahrhunderts wurden mit der Röntgenstrahlung (1895) und der Radioaktivität (Becquerel, 1896) Effekte gefunden, die sich nur durch Vorgänge im Atom erklären ließen.
Bereits im Jahre 1897 schätzte J. J. Thompson ab, dass ein Wasserstoff-Kern 1836-mal schwerer ist
als ein Elektron.
1.3 Entwicklung und Historie der Atomphysik
Seite 7
Im Jahr 1900, dem sogenannten „Planckschen Jahr“, postulierte Planck die Quantennatur und
führte das Plancksche Wirkungsquantum zu deren Beschreibung ein. 1905 nutzte Einstein die Quantentheorie, um den Photoeffekt zu erklären. Diese Quantisierung wurde erneut im Jahre 1914 durch
den Franck-Hertz-Versuch nachgewiesen.
Im Jahre 1911 zeigte Rutherford, dass die Masse eines Atomes zu großen Teilen in einem kleinen
positiv geladenen Atomkern konzentriert ist, während die negativ geladene Atomhülle fast leer ist. Die
moderne Quantenmechanik läutete de Broglie 1924 durch die Theorie des Welle-Teilchen-Dualismus
ein.
2.1 Das Rutherford-Bohr’sche Atommodell
Seite 8
2 Klassische Ansätze
2.1 Das Rutherford-Bohr’sche Atommodell
Die Atomtheorie nach Thomson beschrieb das Atom als kontinuierlich verteilten „Pudding“ aus Elektronen, der zum Beispiel αTeilchen immer unter einem festen Winkel θ = 2800 streut. Jedoch
widersprach die Beobachtung großer Streuwinkel dieser These. Daraus konnte man schließen, dass die Masse in einem kleinen Bereich,
dem Atomkern, vereinigt ist. Dieser Kern ist positiv geladen, die
Streuung von α-Teilchen im Thomsonschen
negativ geladenen Elektronen umfliegen diesen Kern, sodass das
Atommodell
ganze Atom wieder elektrisch neutral ist. Dies würde aber dazu
führen, dass die Elektronen aufgrund der Radialbeschleunigung Bremsstrahlung aussenden, wodurch
sich ihre kinetische Energie verringern würde und sie deswegen aufgrund der Coulombkraft in den Kern
stürzen würden.
Um dieses Dilemma aufzulösen, postulierte Niels Bohr im Jahre
1913:
1. Es gibt bestimmte diskrete Bahnen, auf denen sich die Elektronen strahlungsfrei bewegen können.
2. Strahlungsaufnahme und -abgabe erfolgt durch Übergänge
zwischen diesen diskreten Bahnen.
Aus diesen Postulaten ergeben sicher einige Folgerungen:
1. Jede Bahn hat eine bestimmte Energie En , hierbei ist n ∈ N
die Hauptquantenzahl. Die tiefste Energie ist E1 .
2. Übergänge zwischen Bahnen sind ebenfalls „scharf“, die EnergieEnergieniveaus im H-Atom
änderung beträgt ∆E = En0 − En00 = h · ν = ~ · ω. Ist ∆E positiv,
so wird diese Energie als Photon abgegeben. Ist ∆E negativ, muss diese Energie durch ein Photon
zugeführt werden.
3. Die klassische Physik ist im Model von Bohr aufgrund des Korrespondenzprinzips wieder
enthalten, wenn man das erforderliche ∆E → 0 gehen lässt und damit in das klassische QuasiKontinuum übergeht.
Das Vorgehen ist nun, die Gesamtenergie klassisch auszurechnen, den Bahndrehimpuls des Elektrons
einzusetzen und das Korrespondenzprinzip anzuwenden.
Als Zentralkraft wirkt die Coulombkraft, es entsteht ein Gleichgewicht zur Zentrifugalkraft:
−
1
Z · e2
·
= −me · ϕ̇2 · |~r|
4π · ε0 |~r|2
(∗)
Hierbei ist e der Betrag Ladung des Elektrons beziehungsweise Protons, ~r der Abstand des Elektrons
vom Proton, me die Elektronenruhemasse, Z die Kernladungszahl, ϕ die Winkelkoordinate und ϕ̇ die
2.1 Das Rutherford-Bohr’sche Atommodell
Seite 9
Winkelgeschwindigkeit auf der Kreisbahn des Elektrons. Zu ϕ gehört ein Bahndrehimpuls pϕ . Für die
verschiedenen diskreten Bahnen ϕn gibt es natürlich unterschiedliche Bahndrehimpulse pϕn .
Als Ansatz für den Zusammenhang zwischen diesen pϕn wählen wir
pϕn+1 = pϕn + C
Mit (∗) erhalten wir
ϕ̇n =
pϕn
me · |~r|2
⇒
|~r| =
4π · ε0 · p2ϕn
me · Z · e2
(∗∗)
Die klassische Gesamtenergie ergibt sich als Summe der Energie im Coulomb-Potential und der kinetischen Energie:
Eg,kl = Ep + Ek
2
p2
ϕn
1
· Z·e
Eg,kl = − 4π·ε
2
|~r| +
0
³ 2 ´2 2me ·|~r|
Z·e
Eg,kl = − m2e · 4π·ε
· p21
0
ϕn
Entsprechend ergibt sich eine Energieänderung für den Übergang von n zu n + 1:
#
µ
¶2 "
me
Z · e2
1
1
∆E = Eg,kl,n+1 − Eg,kl,n =
·
· 2 −
2
4π · ε0
pϕn
(pϕn + C)2
Die Frequenz des Umlaufes erhalten wir klassisch aus:
νkl,n =
pϕn
ϕ̇n
=
2π
2π · me · |~r|2
Damit lässt sich auch eine Frequenzänderung für den Übergang von n zu n + 1 angeben:
∆νkl = νkl,n+1 − νkl,n
Aufgrund des Korrespondenzprinzips muss diese Frequenzänderung mit der Energieänderung gemäß
der Quantenphysik in der Beziehung ∆E = h · ∆νkl stehen. Unter der Voraussetzung pϕn À C, also
für quasi dicht liegende Niveaus, erhält man daraus:
C = pϕn+1 − pϕn =
h
= ~ ∀n
2π
Die Niveaus sind also äquidistant. Der Bahndrehimpuls ist gleich dem klassischen Drehimpuls:
~ n|
pϕn = n · ~ = Ln = |L
Drehimpuls der Elektronen
2.2 Spektralserien und Energieniveauschema des H-Atoms
Seite 10
Bisher hatten wir den Kern als fest betrachtet, die Elektronen bewegen
sich auf Kreisbahnen um den Kern. Es ist aber auch möglich, dass sich der
Kern im Atom bewegt. Zu Beschreibung dieses Systems verwenden wir
Relativkoordinaten und eine reduzierte Masse (Zweikörperproblem):
~r = ~re −~rk
mr =
und
me · mk
me + mk
Bei der Gesamtenergie und dem Gesamtdrehimpuls nimmt man nun die
reduzierte Masse statt der Elektronenmasse, und kommt damit wieder
auf gültige Werte. Aus dieser Betrachtung folgt:
1. Die kleinste Umlaufbahn ist
rn |n=1 = r1 =
Zweikörperproblem im H-Atom
4π · ε0 · ~2
me · Ze2
Beim H-Atom ist mr ≈ me und Z = 1, damit ergibt sich der Bohrsche Radius r1 ≡ a0 ≈ 0, 5 Å.
2. Die Gesamtenergie für die n-te Bahn ergibt sich zu
³
´2
Z·e2
En = − 21 · 1+mme e · 4πε
· n12
0 ·~
2
= − 2m ~·|~r
r
mk
1|
2
= −hc · Z 2 ·
1
= E1 · n12
n2
R∞
1
me · 2
1+ m
n
·
Darstellung mit kleinster Energie
Darstellung mit Rydberg-Konstante
n
3. Frequenzbedingung:
νn+1,n = Z 2 · c ·
Beispiel 2.1
R∞
me ·
1+ m
k
µ
1
1
−
(n + 1)2 n2
¶
zur Frequenzbedingung
Für den Term me /mk gilt bei den verschiedenen Wasserstoffisotopen:
• Wasserstoff: me /mp
• Deuterium: me /(2 · mp )
• Tritium: me /(3 · mp )
Damit ist bei den selteneren Wasserstoffisotopen das sonst sichtbare Spektrum in den UV-Bereich verschoben.
2.2 Spektralserien und Energieniveauschema des H-Atoms
Beim Übergang von |0i zu |ni (diese Schreibweise für Zustände wird später erläutert) handelt es sich um eine Anregung, während ein Übergang
von |ni zu |0i eine Abregung darstellt. Eine Anregung führt zu einer
Erhöhung der Energie um
µ
¶
R∞
1
2
∆E = En0 − En00 = En − E1 = hc · Z ·
me · 1 − 2
1+ m
n
H
Übergang zwischen Zuständen
Man definiert die Ionisationsenergie als die Energie, die nötig ist, um ein Elektron von einem Atom
abzutrennen. Diese Energie erhält man durch Betrachtung des Übergangs aus dem Grundzustand |n0 i
des Elektrons mit der Hauptquantenzahl n0 in den Zustand |∞i. Für das H-Atom ist
EI = −E1 = hc · Z 2 ·
R∞
me = −13,6 eV
1+ m
H
2.2 Spektralserien und Energieniveauschema des H-Atoms
Seite 11
Desweiteren definieren wir den Termwert Tn als die dem absoluten Betrag des Energiewertes En
proportionale Wellenzahl (ν = 1/λ):
Tn =
En
R∞
= Z2 ·
me
hc
1+ m
H
mit
[Tn ] = cm−1
Hieraus konnen wir schließen:
1. ∆ν n0 ,n00 = Tn0 − Tn00
2. ∆λn0 ,n00 = 1/(Tn0 − Tn00 )
Anhand der n00 unterscheidet man verschiedene Serien von Spektrallinien, welche sich im spektralen
Raum teilweise überlappen.
• Die Lyman-Serie geht vom Zielzustand n00 = 1 aus (also sind Werte n0 = 2, 3, 4, . . . möglich). Die
Spektrallinien der Lyman-Serie liegen im tiefen Ultraviolettbereich (Deep Ultra Violet, DUV).
• Die Balmer-Serie tritt bei Übergängen zum Energieniveau n = 2 aus höheren Niveaus auf, Die
Balmer-Serie ist sehr gut experimentell zugänglich, da die emittierte Strahlung im UV- und im
sichtbaren Bereich liegt.
• Die Paschen-Serie besteht aus Rückfällen nach n = 3, die Strahlung ist infrarot.
• Die Brackett-Serie besteht aus Rückfällen nach n = 4, die Strahlung ist ebenfalls infrarot.
• Die Pfund-Serie besteht aus Rückfällen nach n = 5, die Strahlung ist nah-infrarot.
In allen Formeln taucht die Kernladungszahl Z auf. Das liegt daran, dass sich die Überlegungen für das
H-Atom auf andere Kerne in guter Näherung übertragen lassen. Allerdings darf keine Wechselwirkung
zwischen Elektronen auftreten, deshalb gilt die Näherung nur, wenn das Atom soweit ionisiert ist, dass
nur noch ein Elektron übrig ist. Das ist zum Beispiel bei He+ mit Z = 2, Li2+ mit Z = 3 oder auch
bei U91+ mit Z = 92 der Fall.
Allgemein stimmt das Rutherford-Bohr-Modell im Groben sehr gut mit experimentellen Beobachtungen
überein, allerdings nur für 1e− -Übergange.
Anwendungen der Wasserstoffübergänge
• Beim Laser wird Emission bei großen Quantenzahlen (meist n0 > 100) stimuliert. Die Lebensdauer τn0 solcher Zustände ist sehr kurz, weswegen die spektrale Auflösung, also die Genauigkeit
des emittierten Photonenstromes im Spektrum, sehr hoch ist:
∆ν
∆ω
=
≈ 10−15
ν0
ω0
• In der Astrophysik ist auch meistens n > 100, wodurch sich Frequenzen in der Größenordnung
von 100 GHz ergeben können. Typisch ist hier das Auftreten von Elektroneneinfängen, bei
denen ein Proton und ein Elektron sich zu einem angeregten H-Atom verbinden.
p + e− → Hnj
Hierbei ist n die Hauptquantenzahl des Energieniveaus des Elektrons, und j ist die Änderung
des Hauptquantenzahl. j wird als griechischer Buchstabe notiert, zum Beispiel α für ∆n = 1
und γ für ∆n = 3 (entsprechend der Ordnung im griechischen Alphabet). Man schreibt also zum
Beispiel H109β, wenn das Elektron von n = 109 nach n = 107 springt.
Bei so hohen Quantenzahlen bewegen sich die Elektronen nicht mehr auf Kreisbahnen, sondern
auf elliptischen Bahnen. Dadurch wird eine relativistische Betrachtung notwendig.
2.2 Spektralserien und Energieniveauschema des H-Atoms
Seite 12
Im Jahre 1916 schlugen Bohr und Sommerfeld eine neue Theorie zur Erklärung der Elektronenbahnen mithilfe des Keplerschen Flächensatzes vor, bei dem die Energieniveaus En nochmals durch
Feinstrukturkonstanten α in Unterenergieniveaus Enα aufgespalten werden. Die Bohr-SommerfeldTheorie hat jedoch einige Probleme: Sie kann Übergangsintensitäten und chemische Bindungen nicht
erklären und ist nur auf Systeme anwendbar, die lediglich ein Elektron enthalten und keine äußeren
Felder beinhalten. Um diese Dinge zu erklären, benötigt man die Quantenmechanik.
3.1 Die zeitabhängige Schrödingergleichung
Seite 13
3 Quantenmechanik
Im Gegensatz zur klassischen Physik, in der wir von absoluter Gewissheit ausgehen, kann man in einer
Quantentheorie für alles nur eine gewisse Wahrscheinlichkeit angeben. Es gibt verschiedene Quantentheorien: Die bereits erwähnte Bohr-Sommerfeld-Quantentheorie hat, wie oben dargestellt, viele
Probleme und gilt als veraltet. Heute verwendet man die Theorien der Quantenmechanik nach Heisenberg und nach Schrödinger.
3.1 Die zeitabhängige Schrödingergleichung
Beim Aufstellen der Schrödingergleichung geht man von dem 1924 von de Broglie postulierten WelleTeilchen-Dualismus aus. Danach hat ein Teilchen eine Frequenz sowie eine Wellenlänge:
ν=f =
E
h
und
λ=
c
hc
h ! h
=
= E=
ν
hν
c
p
Hierbei ist c die Wellengeschwindigkeit, die nicht unbedingt gleich mit der Lichtgeschwindigkeit ist!
Daraus folgt eine Beziehung für Energie und Impuls:
E =p·c
Beispiel 3.1
Ein Virus im Körper hat die Masse m = 1 µg = 10−9 kg und die Geschwindigkeit v = 10−6 ms−1 . Dann ist
λ=
h
h
=
= 6,63 · 10−19 m
p
m·v
Die Wellenlänge dieses Virus ist um den Faktor 1000 kleiner als ein Atomkern, also wird man keine Welleneffekte beobachten können. Für ein nichtrelativistisches Elektron mit der kinetischen Energie Ekin = 10 keV
erhält man:
Ekin =
p2
2me
⇒
p=
p
2me · Ekin
⇒
λ=
h
h
hc
=√
=√
p
2me · Ekin
2me c2 · Ekin
Es ist hc = 1240 eV · mm und me c2 = 511 keV, weswegen sich eine Wellenlänge von λ = 0,01226 nm ergibt.
Das heißt, dass man in Atomen durchaus Effekte der Wellenmechanik beobachten kann.
Der Ansatz von Schrödinger ist der Energiesatz:
Etot = Ekin + Epot =
p~2
+ V (~r)
2m
(¤)
3.2 Die stationäre Schrödingergleichung
Seite 14
Schrödinger postulierte folgende Substitutionsregeln zur Umwandlung in eine Operatorgleichung:
∂
E → i~ · ∂t
~
~p → −i~ · ∇
V (~r) → Multiplikation mit V (~r)
Das ergibt:
~ 2
∂
(−i~ · ∇)
−~2 ~ 2
=
+ V (~r) =
· ∇ + V (~r) =: H
∂t
2m
2m
Der rechte Term wird als Hamilton-Operator H bezeichnet. Diese Operatorgleichung kann auf eine
(im Allgemeinen komplexe) Wellenfunktion Ψ angewendet werden. Diese Wellenfunktion beschreibt
das Teilchensystem vollständig:
i~ ·
i~ ·
∂Ψ
∂t
=
−~2
2m
~ 2 Ψ + V (~r) · Ψ = HΨ
·∇
Zeitabhängige Schrödingergleichung
Nun fehlt noch eine physikalische Interpretation der Wellenfunktion Ψ(~r, t). Man kann |Ψ|2 = Ψ·Ψ∗ als
Wahrscheinlichkeitsdichte auffassen, dass das Teilchen mit der Masse m unter Einfluss des Potentials
V (~r) zur Zeit t im Raumelement dV = dx · dy · dz mit dem Mittelpunkt ~r zu finden ist.
Die Wahrscheinlichkeit, dass sich das Teilchen irgendwo im Raum ist, ist gleich 100%:
R∞
|Ψ|2 dV = 1
−∞
Normierungsbedingung
3.2 Die stationäre Schrödingergleichung
Die Zeitabhängigkeit soll aus der Schrödingergleichung eliminiert werden. Wir machen deshalb einen
Separationsansatz:
Ψ(x, y, z, t) = ψ(x, y, z) · v(t)
Einsetzen in die Schrödingergleichung ergibt:
i~ ·
dv
· ψ = v · Hψ
dt
Wir dividieren durch v und ψ:
i~ dv
1
·
= · Hψ
v dt
ψ
Den linken Term kann man gerade als Energie interpretieren. Damit ist E die Separationskonstante
und es ergeben sich zwei Differentialgleichungen:
dv
E
=
· dt
v
i~
und
1
· Hψ = E
ψ
Die erste Differentialgleichung wird gelöst durch
µ
¶
E
v(t) = v0 · exp −i · t
~
3.4 Die Schrödingergleichung im Zentralpotential
Seite 15
Es kann v0 = 1 normiert werden, damit ergibt sich:
¶
µ
E
Ψ(~r, t) = ψ(~r) · exp −i · t
~
Die Wahrscheinlichkeitsdichte ist:
µ
¶
µ
¶
E
E
|Ψ| = Ψ · Ψ = ψ (~r) · exp +i · t · ψ(~r) · exp −i · t = |ψ|2
~
~
2
∗
∗
Die zweite Differentialgleichung ergibt bei Multiplikation mit ψ die
Hψ = Eψ
Stationäre Schrödingergleichung
Hieraus folgen zum Beispiel die Energieeigenwerte im Wasserstoffatom. Diese sind abhängig vom jeweiligen atomaren System, dessen Potential V (~r) und Randbedingungen. Energiewerte können diskret
(wie beim H-Atom) oder kontinuierlich (wie etwa beim harmonischen Oszillator) sein.
Im Allgemeinen ist es ziemlich schwierig, exakte Werte für komplexere Systeme zu ermitteln. Meistens
gelangt man nur mit numerischen Methoden, zum Beispiel durch Iteration, zum Ziel.
3.3 Die Schrödingergleichung im Nullpotential
Wir betrachten das Potential V (~r) = 0, also ist F~ = − grad V (~r) = 0. Wir beschränken uns für die
Lösung auf den eindimensionalen Fall. Der Ansatz ist wiederum
Ψ(x, t) = A · exp [i(kx − ωt)]
Zunächst bestimmen wir die in der Schrödingergleichung vorkommenden Ableitungen:
∂Ψ
∂t
∂Ψ
∂x
∂2Ψ
∂x2
= −iω · Ψ
= ik · Ψ
= −k 2 · Ψ
Eingesetzt ergibt sich:
2
~
i~ · (−iω) · Ψ = − 2m
· (−k 2 ) · Ψ
2
2
p2
k
= 2m
=E
~ω = ~2m
Dieser Ansatz ist also gut für eindimensionale Fälle, somit auch für dreidimensionale Fälle.
3.4 Die Schrödingergleichung im Zentralpotential
Wir haben nun als Potential V (~r) das radialsymmertische Coulomb-Potential. Aufgrund der nicht
vorhandenen Zeitabhängigkeit dieses Potentials genügt die Lösung der zeitunabhängigen Schrödingergleichung Hψ = Eψ. Wir erwarten aufgrund der Struktur der Differentialgleichung, Energieeigenwerte
En und Eigenfunktionen ψ für den Hamilton-Operator des Coulombpotentials zu erhalten. Der Hamiltonoperator ist gegeben durch:
~2 ~ 2
Ze2
H=−
·∇ −
2m
4πε0 · |~r|
3.4 Die Schrödingergleichung im Zentralpotential
Seite 16
Es erscheint sinnvoll, dieses Problem zur Lösung in Kugelkoordinaten zu übertragen:
µ
¶
µ
¶
∂2
∂2
∂2
1 ∂
∂
∂
1
∂
1
∂2
2
2
~
∇ =
+
+
=
r
·
sin
ϑ
·
·
+
·
+
·
r2 ∂r
∂r
r2 · sin ϑ ∂ϑ
∂ϑ
r2 · sin ϑ ∂ϕ2
∂x2 ∂y 2 ∂z 2
|
{z
} |
{z
} |
{z
}
radialer Anteil
polarer Anteil
azimutaler Anteil
Wir verwenden wieder einen Separationsansatz:
ψ(x, y, z) = ψ(r, ϑ, ϕ) = R(r) · Θ(ϑ) · Φ(ϕ)
Es ergibt sich:
µ
¶
µ
¶
·
¸
RΘ
dΘ
RΘ
~2 ΘΦ d
d
d2 Φ
2 dR
·
r ·
+ 2
sin ϑ ·
+ 2
−
·
·
·
+Vc (~r)·RΘΦ = RΘΦ·E
2m r2 dr
dr
r · sin ϑ dϑ
dϑ
r · sin2 ϑ dϕ2
Zur Vereinfachung wird multipliziert mit 2m/~2 · (r2 · sin2 ϑ)/(RΘΦ).
µ
¶
µ
¶
sin2 ϑ d
dR
sin ϑ d
dΘ 2m 2
1 d2 Φ
2
−
r2 ·
−
sin ϑ ·
·
·
·
r
·
sin
ϑ
·
[E
−
V
(~
r)]
=
·
c
R
dr
dr
Θ
dϑ
dϑ ~2
Φ dϕ2
Den linken von r und ϑ abhängigen Teil nennen wir (∗∗), der rechte Teil mit der Abhängigkeit von ϕ
soll (∗) heißen. (∗) ergibt:
d2 Φ
− Φ · const. = 0
dϕ2
Der Lösungsansatz ist Φ(ϕ) = A·exp (iml · ϕ). Damit ist die bis jetzt unbekannte Separationskonstante
durch −m2l gegeben. Wir werden sehen, dass ml ∈ Z ist. Die Ganzzahl ml wird als magnetische
Quantenzahl bezeichnet. Als Randbedingung nehmen wir die offensichtlich zu fordernde Periodizität
Ψ(0) = Ψ(2π) = A und normieren A = 1.
Zur Lösung von (∗∗) können wir die gefundene Separationskonstante −m2l einsetzen. Wir dividieren
durch sin2 ϑ und separieren r und ϑ:
µ
¶
µ
¶
m2l
1
d
dΘ
1 d
2m
2 dR
−
·
sin ϑ ·
= ·
r ·
+ 2 · r2 · [E − Vc (~r)] = const.
2
dϑ
R dr
dr
~
sin ϑ Θ · sin ϑ dϑ
Der linke Teil heißt jetzt (∗∗∗) und der rechte Teil wird vorübergehend (∗∗∗∗) genannt. Zur Separation
verwenden wir die Separationskonstante l(l + 1). Wiederum werden wir sehen, dass l ∈ Z ist; l wird
als Bahndrehimpulsquantenzahl bezeichnet.
Nach der Lösung werden die Winkelfunktionen Θ und Φ zusammengefasst zu sphärischen Kugelfunktionen Y (ϑ, ϕ) = Θ(ϑ) · Φ(ϕ). Wir nutzen noch die Differentialgleichung (∗ ∗ ∗) und erhalten:
µ
µ
¶
¶
1
d
d
1
d2
−
·
sin ϑ ·
−
·
Y = l(l + 1) · Y
sin ϑ dϑ
dϑ
sin2 ϑ dϕ2
Die mathematische Physik hat gezeigt, dass diese Differentialgleichung durch assoziierte LegendrePolynome gelöst wird. Diese haben die folgende Darstellung:
¡
¢
l+ml cos2 ϑ − 1
(−1)ml
ml
ml /2 d
Pl (cos ϑ) = l
· (1 − cos ϑ)
·
2 · l!
d (cos ϑ)l+ml
Hierbei ist l = 0, 1, 2, . . . der Grad des Legendre-Polynoms. Die ersten Polynome haben die Form:
P00 (cos ϑ)
P10 (cos ϑ)
P20 (cos ϑ)
P30 (cos ϑ)
= 1
= cos¡ϑ
¢
= 21 · ¡3 · cos2 ϑ − 1
¢
= 12 · 5 · cos2 ϑ − 3 · cos ϑ
3.4 Die Schrödingergleichung im Zentralpotential
Seite 17
Die Lösung von (∗ ∗ ∗) ist also:
s
Y =
Ylml (ϑ, ϕ)
ml
= Φml · Θml ,l (ϑ) = (−1)
·
(2l + 1) · (l − ml )
· Plm+l (cos ϑ)
4π · (l + ml )!
Die folgenden Aufgaben werden dem geneigten Leser als simple Übungsaufgabe überlassen:
¢∗
¡
(a) Zeigen Sie, dass gilt: Yl−ml = (−1)ml · Ylml
R
(b) Zeigen Sie, dass (Ylml )∗ · Ylml dΩ = 1 ist. Hierbei ist dΩ ein Raumwinkelelement.
(c) Zeigen Sie, dass durch die Legendre-Polynome ein vollständiges Orthogonalsystem gegeben ist,
R m0
also dass gilt: (Yl0 l )∗ · Ylml dΩ = δl,l0 · δml ,m0l .
Nun schauen wir uns die Differentialgleichung (∗∗∗∗) an, diese lautete:
µ
¶
1 d
2m
2 dR
r ·
+ 2 · r2 · [E − Vc (~r)] = l · (l + 1)
·
R dr
dr
~
Wir behaupten:
d
dr
µ
dR
r ·
dr
2
¶
=r·
d2 r · R
dr2
Zum Beweis:
·
¸
·
¸
µ
¶
d
dR
dR
dR 2 d2 R
d d
dR 2 d2 R
d
2 dR
(r · R) = r·
R+r·
= r·
+r·
+r · 2 = 2r·
+r · 2 =
r ·
r·
dr dr
dr
dr
dr
dr
dr
dr
dr
dr
dr
Zur Vereinfachung der Differentialgleichung substituieren wir r · R(~r) =: u(~r):
· 2
¸
~2 d2 u(~r)
~ l · (l + 1)
E · u(~r) = −
·
+
+ Vc · u(~r)
2m dr2 2
2mr2
In der Klammer steht ein neues effektives Potential, das zusätzlich zur Coulombkraft die „Fliehkraft“
des Elektrons auf der Bahn l beschreibt:
~2
~2 l · (l + 1)
L
=
b
2mr2
2I
~ entspricht dem Bahndrehimpuls (I ist das Trägheitsmoment des Elektrons). Es ergibt sich:
L
p
~ := ~ · l · (l + 1) mit l = 0, 1, 2, 3, . . .
|L|
Damit ist die Benennung von l als „Bahndrehimpulsquantenzahl“ gerechtfertigt. Die Lösung von R(~r)
ergibt sich schließlich (siehe Quantenmechanik) zu:
"µ
#
¶ s
2Z 3
(n − l − 1)! −%/2 l 2l+1
Rn,l (r) = −
·
·e
· % Ln+l (%)
n · aµ
2n · (n + l)!
Hierbei sind:
%=
2Z
·r
n · aµ
und
aµ =
4π · ε0 · ~2
µ · e2
und
µ = mr =
mM
m+M
Außerdem tauchen in der Lösung die assoziierten Laguerre-Polynome auf:

nr
 nr = n − l − 1
2
k
X
(n + l)! · %
2l+1
k+2l+1
Ln+l (%) =
(−1)
·
mit
n = 1, 2, 3, . . .

(nr − k)! · (2l + 1 + k)! · k!
k=0
l = 0, 1, . . . , n − 1
Die Separation der ursprünglichen Schrödingergleichung war also erfolgreich. Was gilt für die R(~r)?
3.4 Die Schrödingergleichung im Zentralpotential
• Die R(~r) sind normiert:
R∞
0
Seite 18
∗ · R dr = 1
Rnl
nl
• Rn,l ∼ exp(−r/n)
• Rn,0 (r = 0) 6= 0 und Rn,l6=0 (r = 0) = 0
Betrachten wir nun die Darstellung der Kugelflächenfunktion Y :
• Ylml ist normiert.
• Für l = 0 ist Y0ml räumlich isotrop, für m = 0 ist Yl0 ∼ cos2 ϑ.
• Es sind nur solche Ylml definiert, für die |ml | ≤ l ist.
Die übliche Darstellung für den Radialteil lautet:
D(r) := r2 · Rn,l (r)2
Radiale Wahrscheinlichkeitsdichte
Die radiale Wahrscheinlichkeitsdichte D(r) ist ein Mass für die Wahrscheinlichkeit, dass das Elektron
sich im Intervall [r, r + dr] befindet. Alle Nullstellen von Rn,l übertragen sich auf D. Außerdem kommt
die Nullstelle r = 0 hinzu (welche eigentlich nur bei Rn,l6=0 vorkommt).
Zur Bezeichnung: Den Bahndrehimpulsquantenzahlen werden Buchstaben zugeordnet.
Bahndrehimpulsquantenzahl
Orbitale
0
s
1
p
2
d
3
f
4
g
5
h
6
i
...
...
Aus der Hauptquantenzahl n und dem Buchstaben für das Orbital ergibt sich die Elektronenkonfiguration, zum Beispiel 3d für n = 3 und l = 2.
Die radiale Wahrscheinlichkeitsdichte D(r) hat unter anderem die folgenden Maxima:
Konfiguration
Abstand r
1s
a0
2p
4a0
3d
9a0
4f
16a0
Nun betrachten wir die Funktion Φ(ϕ). Diese hing von der magnetischen Quantenzahl ab:
Φml = A · eiml ·ϕ mit m = 0, ±1, ±2, . . .
√
Die Normierung ergibt A = 1/ 2π. Dann ist |Φml |2 = 1/2π unabhängig von ϕ, daher hat das Elektron
in gleichgroßen Winkelelementen dϕ1 und dϕ2 eine gleichgroße Aufenthaltswahrscheinlichkeit. (Die
Lösung ist also in der xy-Ebene isotrop.) Die Φml bilden ein Orthonormalsystem:
Z2π
Φml · Φ∗m0 dϕ = δml ,m0l
l
0
Es verbleibt noch Θ(ϑ) zu betrachten. Durch
|Θl,ml |2 · sin ϑ dϑ = Θl,ml · Θ∗l,ml · sin ϑ dϑ
ist die Wahrscheinlichkeit gegeben, das Elektron in dem Intervall [ϑ, ϑ+ dϑ] zu finden. Die Normierung
dieser Funktionen erfolgt wie folgt:
Z2π
Θl,ml · Θ∗l0 ,m0 · sin ϑ dϑ = δl,l0 ·
l
0
Die Funktion Θ nimmt einige bekannte Formen an:
2 · (l + ml )!
(2l + 1) · (l − ml )!
3.5 Die Grobstruktur des H-Atoms
1. Für l = 0 und ml = 0 ergibt sich eine radial symmetrische Wellenfunktion Y00 =
Funktion heißt s-Wellenfunktion oder Kugelfunktion.
Seite 19
p
1/4π. Diese
2. Für l = 1 und ml = 0 ergibt sich Y10 ∼ cos ϑ und daraus Y10 · (Y10 )∗ ∼ cos2 ϑ. Dies entspricht
einer Dipolantenne, die in z-Richtung strahlt.
Für l = 1 und ml = ±1 ergibt sich Y1±1 ∼ sin ϑ und daraus Y1±1 · (Y1±1 )∗ ∼ sin2 ϑ. Dies
entspricht einer Dipolantenne, die in der xy-Ebene strahlt. Die Wellenfunktionen mit l = 1
heißen p-Wellenfunktionen.
3. Für l = 2 und ml = 0 entspricht Y20 dem Feld einer Quadrupolantenne. Die Wellenfunktionen
mit l = 2 heißen d-Wellenfunktionen.
Die allgemeine Lösung hat Eigenfunktionen ψ und damit auch Eigenwerte Ei . Setzt man ψ in die
Schrödingergleichung ein, erhält man:
En = −hc ·
Z2
R∞
·
m
1+ M
n2
Dies ist analog zur Bohr-Rutherford-Theorie. Allerdings ist die Energie nur von der Hauptquantenzahl
n abhängig, also haben alle Zustände die gleiche Energie, unabhängig von der Bahndrehimpulsquantenzahl l. Dieses Dilemma (mehrere Zustände mit derselben Energie) bezeichnet man als Entartung.
Zur Darstellung der Wellenfunktionen benutzt man eine von White entwickelte Methode, bei der eine
Spindel mit der Silhouette des Graphs von D(r) drehbar gelagert und durch einen Motor auf der zAchse gedreht wird; es entsteht eine Bewegung in ϕ-Richtung. Der polare Winkel ϑ wird mittels eines
Holzprofils, welches die Form von Ylml hat, zwischen 0 und π/2 eingestellt. Die Bewegung der Spindel
wird mittels einer Kamera mit Langzeitbelichtung aufgezeichnet.
3.5 Die Grobstruktur des H-Atoms
Die Quantenmechanik, insbesondere die Schrödingergleichung, wird angewendet auf das Zentralproblem mit dem Coulombpotential des H-Atomes. Man erhält eine Lösung mit drei Quantenzahlen:
n = 1, 2, 3, . . .
l = 0, 1, 2, . . .
ml = −l, −l + 1, . . . , l − 1, l
Zu jedem n existieren n verschiedene l-Werte, und zu jedem l existieren 2l + 1 verschiedene ml -Werte.
Das System ist also überbestimmt. Wir wissen, dass es möglich ist, die Energien alleine durch n
zu bestimmen, während die Eigenfunktionen durch alle drei Quantenzahlen beeinflusst werden. Die
Energie eines Quantenzustandes ergibt sich aus:
En ∼ −
1
n2
Die En sind also entartet, dabei ist die l-Entartung n-fach und die ml -Entartung ist (2l + 1)-fach.
Zum Beispiel haben für n = 2 die Zustände l = 0 (Konfiguration 2s) und l = 1 (Konfiguration 2p) die
gleiche Energie, also ist die Energie zweifach l-entartet.
4.1 „Normale“ Feinstrukturaufspaltung (Spin-Bahn-Kopplung)
Seite 20
4 Fein- und Hyperfeinstruktur des
H-Atoms
Michelson und Morley beobachteten 1887, dass die Balmer-Linie des Wasserstoffspektrums eigentlich aus zwei sehr dicht nebeneinander liegenden Linien besteht. Ein erster vager Erklärungsversuch
waren die von der Bohr-Sommerfeld-Theorie prognostizierten elliptischen Elektronenbahnen. Heute
kennt man die genauen Ursachen und Probleme früherer Theorien:
~
• Das Elektron hat einen Elektronenspin S.
• Der Atomkern hat eine bestimmte Nukleonenstruktur.
• Es müssen einige relativistische und elektrodynamische Korrekturen vorgenommen werden. (Dafür nimmt man die Dirac-Gleichung, die relativistische Version der Schrödingergleichung.
Hges = Hkin + Hpot
Die potentielle Energie setzt sich zusammen aus:
Anteil
HCoulomb
Hfs
HQED
Hhfs
Hnukl
Ursache
Coulomb-Wechselwirkung
Feinstruktur-Wechselwirkung
Quantenelektrodynamik-Wechselwirkung
Hyperfeinstruktur-Wechselwirkung
Abweichungen aufgrund unterschiedlicher Nukleonenstruktur
Größe
10 eV
10−4 eV
10−5 eV
10−5 eV
10−8 eV
4.1 „Normale“ Feinstrukturaufspaltung (Spin-Bahn-Kopplung)
Die Niederländer Gaudsmith und Uhlenbeek postulieren 1925, dass
das Elektron einen Spin haben muss. Damit ergibt sich eine neue Spinquantenzahl s = ±1/2. Daraus ergibt sich eine Spinquantenenergie
1
Es = ± · ~
2
~ 2 = l · (l + 1) · ~2 um den SpinAußerdem wird der Bahndrehimpuls |L|
drehimpuls erweitert:
~ 2 = s · (s + 1) · ~2
|S|
⇒
~ =
|S|
p
s · (s + 1) · ~
Drehimpulskopplung im Atom
Neben der magnetischen Quantenzahl ml führt man eine magnetische Quantenzahl ms = ±1/2 ein.
~ (des Atomes) und S
~ (des Elektrons), es liegt also
Man hat insgesamt zwei gekoppelte Drehimpulse L
~
~
ein Kreisel vor. Die Kopplung zwischen L und S entspricht der normalen Feinstrukturaufspaltung. Sie
folgt aus der Änderung des elektrischen Feldes (in der Größenordnung von 107 V/m zwischen Kern
und Elektron, was zu einem Magnetfeld führt. Dieser Effekt soll jetzt quantifiziert werden.
4.1 „Normale“ Feinstrukturaufspaltung (Spin-Bahn-Kopplung)
Seite 21
Mit der Umlaufperiode T = 2π · r/|~v | kann das bewegte Elektron als
Strom aufgefasst werden:
I=
dQ
e
e · |~v |
= =
dt
T
2π · r
Entsprechend ergibt sich ein magnetisches Moment in der durch die Bewegung des Elektrons beschriebenen „Stromschleife“ (~el sei die Normale
auf der Ebene, in der die Stromschleife liegt):
e·v
evr
e
e
~
µl = I · |F~ | = I · πr2 =
· πr2 =
=
· mrv =
· |L|
2π · r
2
2m
2m
Zur Quantifizierung der Kopplung
~ gibt es zwei Möglichkeiten: Im Bohrschen Modell ist |L|
~ = l · ~, damit ergibt sich
Für |L|
µ
~l = −
1
el · ~
µB ~
· ~el = −l · µB · ~el = −
·L
2m
~
Das magnetische Moment ist also quantisiert. Das kleinstmögliche magnetische Moment ist:
µB =
e·~
2m
= 0,9274 · 10−23 J/T
Bohrsches Magneton
Oben haben wir gesehen, dass µ
~ l linear abhängig vom Bahndrehimpuls ist. Eine ähnliche Formel gilt
auch für Spindrehimpulse, wenn man einen Korrekturfaktor einführt.
B
~
µ
~ l = − gl ·µ
~ ·L
mit
gl = 1
B
~
µ
~ s = − gs ·µ
·S
~
mit
gs = 2
Aus den Maxwell-Gleichungen folgt, dass die Bahnbewegung des Elektrons dazu führt, dass auf das
Elektron ein Magnetfeld wirkt, was zu einer Änderung der potentiellen Energie führt:
~ = − 1 · ~v × E
~
B
c2
⇒
1
~ = 1 · gs · µB · S
~ ·B
~
∆E = − ·µs · B
2
2
~
Der Faktor 1/2 wurde 1926 von Thomas eingefügt, um relativistische Effekte zu beschreiben. Nun
~ an, welche mit dem elektrischen Potential als F~ =
sehen wir uns die Lorentzkraft F~ = q · (~v × B)
−∂V /∂r · ~r/|~r| quantifiziert ist. Das Magnetfeld ist damit:
~ = − 1 · 1 · ∂ V · ~v × ~r
B
r ec2 ∂r
~ = m · (~r × ~v ) = −m · (~v × ~r), durch Kombination mit der obigen Gleichung
Der Bahndrehimpuls war L
ergibt sich:
~ = 1 · 1 · ∂V · L
~
B
r emc2 ∂r
Dies können wir, zusammen mit ∂V /∂r = e2 /(4πε0 · r2 ), in die obige Energieänderung einsetzen:
∆ELS =
1
~ ·L
~
e2
S
·
4πε0 · 2mc2
r3
(◦◦)
Wobei zu beachten ist, dass das magnetische Moment und der Drehimpuls per Konvention antiparallel sind.
4.1 „Normale“ Feinstrukturaufspaltung (Spin-Bahn-Kopplung)
Seite 22
Diese Energieänderung liegt in der Größenordnung von 10−4 eV. Das Magnetfeld hat eine Stärke von
~ generiert ein Maetwa 1 T. Die Wechselwirkung kann man sich so vorstellen: Der Bahndrehimpuls L
~ welcher in S
~ bzw. mu
~ und L
~ eine Präzessignetfeld B,
~ s ein Drehmoment erwirkt. Dadurch führen S
onsbewegung um eine gemeinsame Achse, die auch quantisiert sein muss:
p
~ +S
~ ⇒ |J|
~ = j · (j + 1) · ~
J~ = L
Man wählt ein körperfestes Koordinatensystem, für das J~ um die z-Achse präzediert. Dann präzediert
~ um die J-Achse
~
~ um die L-Achse,
~
L
und S
wobei die letzte Präzession um den Faktor 1000 schneller
läuft als die anderen. Im zeitlichen Mittel ist:
hJx i = hJy i = 0
und
hJz i = mj · ~ 6= 0
Man führt also für die Quantenzahl j auch eine magnetische Quantenzahl mj ein, welche die Werte
mj = −j, −j + 1, . . . , j − 1, j annehmen kann. Nun wollen wir die Definition von J~ ausnutzen, um die
Energieänderung zu vereinfachen:
~ +S
~
J~ = L
~ ·L
~ ~ ~
~ ~
J~ · J~ = L
³ +S·S+2·S·L ´
~ ·L
~ = 1 · J~ · J~ − L
~ ·L
~ −S
~ ·S
~
S
2
~ ·L
~ = 1 · [j · (j + 1) − l · (l + 1) − s · (s + 1)]
S
2
∆ELS =
~2
4m2 ·c2
·
1
r
·
∂V
∂r
· [j · (j + 1) − l · (l + 1) − s · (s + 1)]
Damit wird das Energieniveau n für l 6= 0 aufgespalten in zwei Zustände l + 1/2 und l − 1/2. Bis jetzt
haben wir nur das H-Atom betrachtet; allgemein gilt:
∆ELS = −
α2 · Z 2
n
~ ·L
~
·S
· En ·
1
n2
l · (l + 2 ) · (l + 1)
Hiermit wird eine neue Konstante eingeführt.
α :=
e2
4πε0 ·~c
=
1
137,0359895
≈
1
137
Feinstrukturkonstante
Für J~ gilt wiederum, dass die x- und y-Komponenten im Mittel verschwinden:
hJx i = hJy i = 0
und
hJz i = mj · ~
Hierbei gilt:
mj = ml + ms
Als allgemeine Schreibweise für die Zustände hat sich durchgesetzt:
n(2s+1) Lj
Hierbei sind n die Hauptquantenzahl und 2s + 1 die Multiplizität. L ist der Buchstabe für die Bahndrehimpulsquantenzahl l (als Großbuchstabe: S, P , D, F , G, ...) und j ist die Drehimpulsquantenzahl.
Wir wollen nun die Zustände für das H-Atom auflisten. Hier gilt j = l ± 1/2, wobei j > 0 sein soll.
4.1 „Normale“ Feinstrukturaufspaltung (Spin-Bahn-Kopplung)
n
1
2
2
2
3
3
3
3
3
4
4
4
4
4
4
4
l
0
0
1
1
0
1
1
2
2
0
1
1
2
2
3
3
j
1/2
1/2
1/2
3/2
1/2
1/2
3/2
3/2
5/2
1/2
1/2
3/2
3/2
5/2
5/2
7/2
Seite 23
Bezeichung
12 S1/2
22 S1/2
22 P1/2
22 P3/2
32 S1/2
32 P1/2
32 P3/2
32 D3/2
32 D5/2
42 S1/2
42 P1/2
42 P3/2
42 D3/2
42 D5/2
42 F5/2
42 F7/2
Unser Ziel wird es nun sein, herauszufinden, unter welchen Umständen die einzelnen Niveaus besetzt
werden können. Vorher führen wir nun noch zwei weitere Korrenturen zur Feinstruktur ein, zum einen
die relativistische Geschwindigkeit der Elektronen, zum anderen die endliche Ladungsdichte am Ort
des Kerns (für l = 0-Zustände).
4.1.1 Relativistische Korrekturen
Die relativistische Form des Hamiltonoperators lautet:
q
H = p2 · c2 + m20 · c4 − m0 · c2 +V (~r)
|
{z
}
kinetische Energie T
Das bewirkt nur eine „kleine“ Änderung gegenüber der nichtrelativistischen Rechnung. Entwicklung
nach p führt auf:
p2
1
p4
T =
+ · 3 2 + . . . O(p6 )
2m0 8 m0 c
| {z }
≡∆T
Der erste Term entspricht der klassisch erwarteten kinetischen Energie T0 , der zweite Term ist ein
Störungsterm.
1 p4
T04
∆T = −
=
−
¿ T0
8 m20 · c2
2m0 · c2
Die klassische kinetische Energie kann abgeschätzt werden durch:
T0 ≈ En − V (~r)
⇒
∆T = −
1
2m0 · c2
· [En − V (~r)]2
Beim Rechnen mit Störungen können wir die Erkenntnisse aus der Variationsrechnung anwenden:
D
E
∆Erel = − 2m10 ·c2 · [En − V (~r)]2
h
D
E D 2 4 Ei
Ze2
Z e
= − 2m10 ·c2 · En2 − 2En · − 4πε
+ (4πε
2
0 ·r
0 ·r)
4.2 Lamb-Shift. Anomale Feinstrukturverschiebung
Seite 24
Klassich erhält man den Erwartungswert einer periodischen Funktion aus:
Z
1
hf (t)i = · f (t) d3 r
T
In der Quantenmechanik muss mit der Wahrscheinlichkeitsdichte gewichtet werden:
Z
hf (~r)i = f (~r) · |ψ(~r, t)|2 d3 r
Es ergibt sich damit:
¿ À
1 Z
1
= 2·
r
n a0
¿
und
1
r2
À
=
1
Z2
·
(l + 1/2) · n3 a20
Daraus folgt für die Energiedifferenz zwischen nichtrelativistischer und relativistischer Rechnung:
¸
·
3
n
α2 · Z 2
·
−
∆Erel = −En ·
n2
4 l + 1/2
4.1.2 Korrekturen für die endliche Ladungsdichte
Bei r = 0 findet sich für l = 0 (also die Zustände 1s, 2s, 3s und so weiter) eine endliche Ladung.
Klassisch betrachtet kann dass Elektron nie am Ort des Kernes sein. In der Quantenmechanik muss
man zur S-Wellenfunktion einen Korrekturterm hinzunehmen, der von Darwin entwickelt wurde (und
hier nicht hergeleitet werden soll):
∆EDarwin =
π · ~2 Ze2
(Zα)2
2
·
·
|ψ
(r
=
0)|
=
E
·
n
n,l,m
l
2m · c2 4πε0
n
Daraus folgt, dass es ein endlich großer Teil der Elektronenladung bei r = 0 liegt.
Die Gesamtenergie des Elektrons ergibt sich mit allen Korrekturen zu:
En,j = En + ∆Ef s = En + ∆ELS + ∆Erel + ∆EDarwin
h
En,j = En · 1 +
Z 2 ·α2
n2
·
³
n
j+1/2
−
3
4
´i
Gesamtenergie des Elektrons mit Feinstrukturkorrekturen
Die Energie hängt immer noch nicht von der Bahndrehimpulsquantenzahl ab, somit gibt es ab n = 3
weiterhin eine Entartung. Diese Entartung kann man auflösen, wenn man das Kernfeld nicht mehr als
ideales Feld annimmt, sondern im Rahmen der Quantenelektrodynamik als quantisiert betrachtet. Dies
führt zum sogenannten Lamb-Shift nach Willis E. Lamb.
4.2 Lamb-Shift. Anomale Feinstrukturverschiebung
Bisher haben wir den Energieterm mithilfe der Spin-Bahn-Kopplung, der relativistischen Rechnung
und der Darwinschen Näherung der Ladungsdichte für r = 0 korrigiert. Nun soll, wie in der Quantenelektrodynamik üblich, ein Feld als quantisiert angesehen werden:
µ
¶
X
1
~
|E| =
~ω · nω +
2
n
ω
4.3 Hyperfeinstruktur und Isotopieeffekt
Seite 25
~ = ~ω/2. Also existiert immer ein elektrisches Restfeld
Der tiefste Zustand liegt bei nω = 0, also |E|
im Vakuum, die sogenannte Vakuumpolarisation.
Aufgrund dieser Quantisierung kann sich das Elektron nicht auf einem festen Radius |~r0 | bewegen,
sondern weicht zu einem neuen Radius |~r| aus. Hierbei sind ~r0 und ~r die Ortsvektoren des Elektrons
ohne und mit Vakuumfeld. Die Differenz heißt d~r = ~r−~r0 . Das Potential kann um~r0 entwickelt werden.
Man beachte dabei, dass die Abweichungen im Mittel verschwinden, ihre Quadrate jedoch nicht.
1 ~2
2
~
V (~r) = V (~r0 + d~r) = V (~r0 ) + ∇V
| {z· d~r} + 2 · ∇ V · (d~r)
=0 im Mittel
V (~r) = V (r0 ) +
1
2
~ 2 V · (d~r)2
·∇
Die Bindungsenergie sinkt aufgrund dieses Effektes also ab, und zwar um etwa 10−2 % bis 10−5 %.
Z4
n3
Man beachte, dass diese Korrektur nur bei S-Zuständen angewandt werden muss, da man nur dort
eine Kreisbewegung hat. Damit haben zum Beispiel die Zustände 22 S1/2 und 22 P1/2 nicht mehr die
gleiche Energie, Entartungen in höheren Bahndrehimpulsquantenzahlen bestehen jedoch weiterhin.
∆ELamb ∼
4.3 Hyperfeinstruktur und Isotopieeffekt
Bisher haben wir den Atomkern als strukturlos betrachtet. Jetzt wollen wir nach den Überlegungen
von Pauli (1924) eine Kernstruktur einführen. Die Gesamtmasse setzt sich aus der Masse der einzelnen
Neutronen und Protonen zusammen. Damit haben wir neben dem Gesamtdrehimpuls J~ des Elektrons
~ Neben der Drehimpulsquanten(Masse me ) auch für den Atomkern (Masse mN ) einen Drehimpuls I.
zahl j für das Elektron (die wie gehabt quantisiert ist) eine neue Zahl i = 0, 1/2, 1, 3/2, . . . ein, die
außerdem mit einer magnetischen Quantenzahl mi = −i, −i + 1, . . . , i − 1, i versehen ist. Es gilt nun:
p
~ = i(i + 1) · ~
|I|
In Analogie zum Elektron gibt es auch hier ein magnetisches Moment:
µ
~ I = gI · µN ·
I~
~
mit
µN =
e~
me
=
· µB
2mp
mp
Hierbei ist gI der g-Faktor des Kernes und µN das kleinstmögliche Kernmagneton (in Analogie zum
Bohrschen Magneton).
Das magnetische Moment war beim Elektron relevant wegen des Elektronenspins. Auch hier gibt es
einen zusätzlichen Eintrag im magnetischen Moment aufgrund eines Kernspins. Aufgrund des Massenverhältnisses von Kern und Elektron erwarten wir eine (gegenüber ∆Efs um drei Größenordnungen
kleinere) Korrektur der Elektronenenergie, falls µN zu einem Magnetfeld koppelt:
~ r = 0)
∆Ehfs = −~
µI · B(~
Die relevanten Magnetfelder werden erzeugt durch den Elektronenspin sowie die Bahnbewegung des
Elektrons.
~ +S
~ der Gesamtdrehimpuls. Nun werden I~ und J~ gekoppelt zu einem neuen
Beim Elektron war J~ = L
Drehimpuls:
 
Fx
~
~
~

F = J + I = Fy 
Fz
4.3 Hyperfeinstruktur und Isotopieeffekt
Seite 26
Wiederum sind die Fx - und Fy -Komponenten von F~ im zeitlichen Mittel gleich Null. Wir können zudem
~ ∼ J und |µ~i | ∼ I ist.
festellen, dass |B|
~ r = 0) = A · I~ · J~
∆Ehfs = −~
µI · B(~
Das Quadrat von F~ ist
2
2
F~ 2 = ~I + ~J + 2I~ · J~
mit
~I 2 = i(i + 1) · ~2
und
~J 2 = j(j + 1) · ~2
Es ergibt sich also:
∆Ehfs =
1
·A·C
2
mit
C = f (f + 1) − i(i + 1) − j(j + 1)
und
A=
µI · B(~r = 0)
I~ · J~
~
~ S-Präzession
~
Man beachte, dass die I~J-Präzession
im Vergleich zur L
sehr langsam verläuft.
Beispiel 4.1
Hyperfeinstrukturaufspaltung im H-Atom
Wir haben nur i = 1/2 und j = 1/2. Daraus ergibt ich für f :
(
0
f =i±j =
1
Der Grundzustand (n = 1) spaltet sich in zwei Niveaus auf und man erhält ∆Ehf s ≈ 1420 MHz. Dieser Effekt
ist aber nur wichtig für niedrige Hauptquantenzahlen, da die Aufspaltung bei kleinen Hauptquantenzahlen
wesentlich größer ist als bei großen (wegen der höheren Nähe zum Kern).
Zur Hyperfeinstrukturaufspaltung kommen zwei Korrekturen:
(a) Der Kern enthält noch nicht berücksichtigte magnetische und elektrische Multipole (aufgrund
seines endlichen Volumens und der inhomogenen Ladungsverteilung). Die Abweichung vom Coulombpotential führt auf höhere Multipole, vor allem den elektrischen Quadrupol und den magnetischen Dipol. Für die Energie der Elektronen im Feld des Kerns galt bisher:
Z
%e
2
ECoulomb = Z · e ·
dΩ
4π · ε0 · r
Die Ladungsdichte der Elektronen %e ist isotrop. Nun betrachten wir als erste Abweichung die
Energie des Kerns im Feld der Elektronen:
Z
Ek = e · %k · ϕe dΩ
Die Energiedifferenz ∆E ist also ∆E = Ek − ECoulomb als eine Abweichung vom idealen Modell
einer punktförmigen Ladungsverteilcung im Kern. Für eine Quadrupolladungsdichte gilt zum
Beispiel:
µ
¶
3
1
eQ · ϕzz (r = 0)
2
·
· cos ϕ −
∆E = ∆EQ =
4
2
2
Wir können nun ϕe nach kleinen r entwickeln.
Z
¡
¢
eQ = e · r2 · 3 · cos2 ϕ − 1 %k dΩ
Hierbei ist Q ein Wirkungsquerschnitt (in cm2 ). Der Fall Q = 0 ist trivial (man hat wieder eine
kugelförmige Verteilung). Ansonsten hat man eine Anisotropie (für Q > 0 eine „Zigarre“, für
Q < 0 eine „Oblate“).
4.3 Hyperfeinstruktur und Isotopieeffekt
Seite 27
(b) Isotopieeffekt: Ein Atomkern besteht aus Z Protonen (Z ≥ 1), jeweils mit der Masse mp , und N
Neutronen (N ≥ 0) mit der Masse mn . Die Massen von Neutron und Proton sind in etwa gleich.
Somit haben wir insgesamt A = Z + N Nukleonen mit der Gesamtmasse mN ≈ A · mp . Für
Z = const. und N variabel haben wir verschiedene Isotope. Nun gibt es zwei Korrektureffekte:
• massenabhängiger Isotopieverschiebungseffekt (IVE): Analog zum Bohr-Rutherfordschen
Masseneffekt haben wir eine reduzierte Masse:
mr =
me · mN
me + mN
Die Energieeigenwerte ergeben sich nun zu:
·
¸
Ry · Z 2
me
En = −hc ·
· 1−
n2
mN
Zwei Isotope unterscheiden sich durch die verschiedenen Kernmassen:
m0N
0
= A · mp
und
m00N
00
= A · mp
⇒
·
¸
Ry · Z 2
1
1
1
∆E = hc ·
· me ·
− 00 ∼ 2
n2
m0N
mN
A
{z
}
|
00
0
−A
= AA0 ·A
00
Offensichtlicherweise ist dieser Effekt besonders stark für kleine Kerne. Für ein H-Atom
haben wir in der Balmer-Serie etwa ∆ν = 1, 26 · 1012 cm−1 und ∆λ = 0,18 nm. Bei A > 30
ist der massenabhängige IVE kaum noch messbar.
• Volumen- oder Feldeffekt der IVE Dieser Effekt ist analog zum Lamb-Shift: Für A > 30
muss die endliche Ausdehnung der Kernladung beachtet werden. Das e− -Potential muss also
variiert werden.
Zr0
δ(∆E) = %k · δ(∆V ) · 4πr2 dr
0
Hierbei ist δ(∆V ) die Variation der Kreisbahn durch die Kernladung. Dieser Effekt ist
allerdings nur für kernnahe Bahnen wichtig, also für p- und s-Schalen.
5.1 Operatoren. Eigenwerte. Eigenfunktionen. Quantenmechanischer Mittelwert
Seite 28
5 Verallgemeinerung der
Quantenmechanik
Bisher hatten wir die Wellenmechanik des H-Atoms mithilfe der Schrödingergleichung beschrieben.
Nun sollen eingeführt werden:
1. die Matrixdarstellung nach Heisenberg
2. die Dirac-Schreibweise für Vektoren
3. die Darstellung von Konfigurationen im Hilbertraum
4. die Anwendung auf Vielteilchensysteme (etwa für das Periodensystem oder den quantenmechanischen Tunneleffekt)
5.1 Operatoren. Eigenwerte. Eigenfunktionen. Quantenmechanischer
Mittelwert
Wir haben bereits den Hamiltonoperator H kennengelernt.
Hψ = E · ψ
Hierbei ist ψ eine Eigenfunktion und E ein Eigenwert. Im Folgenden seien alle Operatoren durch
Überstriche gekennzeichnet. Zu einem physikalischen Parameter A gibt es immer einen zugehörigen
Operator A. Wir können über H einiges sagen:
• H ist ein linearer Operator. Allgemein gilt:
(A + B)f = Af + Bf
• Der Operator ist hermitesch, das heißt, in Af = λ · f ist λ immer reell. Zum Beweis integrieren
wir über den Konfigurationsraum X (also den Hilbertraum). Dann muss gelten:
R ∗
R
∗
R f ∗(F f ) dX = R (F f )∗ · f dX
f R (λf ) dX =
(λfR) · f dX
∗
∗
λ · f f dX = λ · f ∗ f dX
⇒ λ = λ∗
• Die Eigenfunktionen fn bilden ein Orthonormalsystem:
Z
fn∗ · fm dX = δnm
Im H-Atom sind diese Eigenfunktionen die ψn,l,ml ,s,ms ,... . Es gilt immer:
Z
X
X
!
ψ=
ci · ψi und
ψ ∗ ψ dX =
c∗i · ci = 1
i
i
5.2 Dirac-Schreibweise und Matrixdarstellung
Seite 29
Für eine periodische Funktion haben wir das zeitliche Mittel definiert:
1
hAi = ·
T
ZT
A(t) dt
0
Dieser Mittelwert gibt auch eine Aussage über den Erwartungswert. Allgemein definiert man bei bekannter Wellenfunktion ψ:
Z
hAi = ψ ∗ Aψ dX
Ist ψ eine Eigenfunktion zu A, so ist A der Eigenwert zu ψ, denn es gilt Aψ = A · ψ. Daraus folgt ein
wichtiges Prinzip:
Eine gleichzeitige scharfe Bestimmung zweier physikalischer Parameter A und B ist nur möglich, wenn
ψ sowohl zu A als auch zu B eine Eigenfunktion ist.
Für den Beweis machen wir einen Ansatz über die beiden Eigenwertgleichungen Aψ = a · ψ und
Bψ = b · ψ. Wir wollen die erste Gleichung von links mit B multiplizieren.
B Aψ = B(Aψ) = B(a · ψ) = a · Bψ = a · b · ψ
Die zweite wird analog von links mit A multipliziert:
A Bψ = b · a · ψ
Damit sind beide Gleichungen identisch. Es gilt B Aψ = A Bψ. Umgeschrieben ist:
£
¤
£
¤
0 = B Aψ − A Bψ = B A − A B ψ =: B, A ψ
Hiermit ist die Poisson-Darstellung erklärt. Wir folgern mit Heisenberg: Beide Größen A, B sind beide
gleich präzise (also scharf bestimmbar), falls B und A kommutieren. Als Besipiel nehmen wir Ort ~x
und Impuls p~x und setzen ein:
~
[px x − x px ] = . . . = 6= 0
i
Die Operatoren kommutieren nicht, daraus folgt, dass Impuls und Ort nicht gleichzeitig scharf bestimmbar sind. Es folgt die bekannte Ungleichung für die Unschärfe:
∆x · ∆px &
~
2
und
∆E · ∆t &
~
2
Nun kommen wir zu Erhaltungssätzen. Bei der Erhaltung von Größen gilt für alle Zeiten:
∂
hAi = 0
∂t
Wie ist das mit der zeitabhängigen Schrödingergleichung vereinbar?
hAi = const.
∂
∂t
⇒
∂ψ
∂t
∂ ψ∗
∂t
= − ~i · Hψ
= ~i · Hψ ∗ = ~i · (Hψ)∗ = ~i · (ψH)∗ = ~i · ψ ∗ H
R ∂ ψ∗
R ∗
hAi =
·
Aψ
dX
+
ψR · A ∂∂tψ dX ¤
∂t
£R
= ~i £R(Hψ)∗ Aψ dX − R ψ ∗ A(Hψ) dX
¤
= ~i · R ψ ∗£HAψ¤dX − ψ ∗ AHψ dX
= ~i · ψ ∗ H, A ψ dX
Diese zeitliche £Mittelung
verschwindet (sprich: die physikalische Größe A ist genau dann zeitlich er¤
halten), wenn H, A = 0 ist. Zum Beispiel wenden wir diese Beziehung auf die Energie, Impuls,
Drehimpuls, strahlende Übergänge etc.
5.2 Dirac-Schreibweise und Matrixdarstellung
Seite 30
5.2 Dirac-Schreibweise und Matrixdarstellung
Bisher hatten wir einen linearen Vektorraum, den sogenannten Hilbertraum. In diesem haben wir
~i , die kommutativ und assoziativ addiert werden können und mit Skalaren so multipliziert
Vektoren V
werden können, sodass wieder Assoziativität und Distributivität gelten.
Als Verbesserung dieses Modells schlägt Dirac Spaltenvektoren (sogenannte Ket-Vektoren |vi) und
Zeilenvektoren (sogenannte Bra-Vektoren hv|). Die Ket- und Bra-Vektoren sind gegeben durch eine
Gruppe von komplexen Zahlen:
 
v1
 .. 
|vi =  .  und hv| = (v1∗ , . . . , vn∗ )
vn
Es gibt entsprechend Basisvektoren |ei i = |ii und hej | = hj|, bei der alle Komponenten Null sind, außer
der i-ten bzw. j-ten Stelle, an der eine Eins steht. Natürlich ist das Skalarprodukt h j | ii = δij . Wir
können also schreiben:
X
X
|vi =
vi · |ii und hv| =
vi∗ · hi|
i
i
Die Multiplikation mit einem Basisvektor ergibt:
X
X
X
h j | vi = hj| ·
vi · |ii =
h j | ii · vi =
δij · vi = vj
i
Analog ist h v | ji =
werden.
vj∗ .
i
i
So können alle Komponenten der Vektoren hv| und |vi können bestimmt
Jetzt lassen wir einen Operator Ω auf |vi wirken.
"
#
X
X
X
¯ ®
Ω |vi = Ω
vi · |ii =
vi · Ω |ii =
vi · ¯i0
i
i
i
Nach Dirac kann man Ω als n × n-Matrix mit n2 Komponenten darstellen.


Ω11 Ω12 · · · Ω1n


Ω1i


.
.. 
Ω21
¯ ®
­
®
. 
 ⇒ ¯i0 = 
Ω=
Ωji
j | i0 = hj| Ω |ii = Ωij
 ..  ⇒
 ..

.
.. 
 .
Ωni
Ωn1 · · · · · · Ωnn
Also ist |i0 i = Ω |ii gerade die i-te Spalte der Ω-Matrix. Analysieren wir Ω |vi:
X
X
X
hj| Ω |vi = hj| Ω
vi |ii =
vi · hj| Ω |ii =
vi · Ωji = vj
i
i
i
In Matrixschreibweise ist:
 
  
v10
h1| Ω |1i · · · h1| Ω |ni
v1
 ..  


.
.
.
.
..
..
..
 . =
 ·  .. 
vn0
hn| Ω |1i · · · hn| Ω |ni
vn

Ein wichtiger Operator ist der Identitätsoperator I, der durch die Einheitsmatrix gegeben ist:
X
I=
|ii · hi|
i
Bemerkung
5.4 Der quantenmechanische Oszillator
•
•
•
•
•
Seite 31
α |vi = |αvi und hαv| = hv| α∗
Ω |vi = |Ωvi und hΩv| = hv| Ω† (adjungierter Operator)
hermitescher Operator: Ω† = Ω
antihermitescher Operator: Ω† = −Ω
unitärer Operator: Ω · Ω† = I
5.3 Postulate der Quantenmechanik
1. Der Zustand eines quantenmechanischen Teilchens im Hilbertraum wird durch den Ket-Vektor
|vi beschrieben.
2. Die Darstellung von Ort und Impuls in der Quantenmechanik wird durch zwei hermitesche Operatoren X und P x erreicht. Hierbei ist:
hx| X |xi = x · δxx
hx| P x |xi = −i~ · δxx
und
3. Die Funktion |ψ(t)i gehorcht der Schrödingergleichung in folgender Art:
i~ ·
∂
|ψ(~r, t)i = H · |ψ(~r, t)i
∂t
mit
H = Hamilton-Operator
4. Für den Eigenwert ω zum Operator Ω eines Teilchens im Zustand |ψi ergibt sich für die Wahrscheinlichkeit:
P (ω) ∼ |h ω | ψi|2
mit Ω |ψi = ω · |ψi
Infolge der Messung des Eigenwertes ω transferiert sich |ψi zu dem neuen Eigenzustand |ωi.
Dieses Phänomen wird als Kollaps der Eigenfunktion |ψi bezeichnet.
Bemerkungen und Konsequenzen
(a) Lineare Superposition: Zwei Zustände α · |ω1 i und β · |ω2 i können zu einem neuen Zustand
kombiniert werden:
α · |ω1 i + β · |ω2 i
|ψi =
α2 + β 2
In dem neuen Zustand haben die beiden Unterzustände eine eigene Wahrscheinlichkeit:
P (ω1 ) =
|α|2
α2 + β 2
und
P (ω2 ) =
|β|2
α2 + β 2
(b) Heisenberg’sche Unschärferelation
[X, P x ] = i~
⇒
@ |ψi , welches gleichzeitig auf X und P x wirken kann
Diese Relation ist ein Ergebnis der statistischen Mechanik; es folgt (pro Dimension):
~
2
Wie erhalten wir eine Beziehung zwischen der Energie und der Zeit?
∆x · ∆px ≥
|~vx | = vx =
∆x
∆t
und
E=
p2x
2m
⇒
dE
px
∆E ! ∆x
=
= vx =
=
dpx
m
∆p
∆t
Damit folgt insgesamt:
∆x · ∆px = ∆E · ∆t ≥
~
2
5.4 Der quantenmechanische Oszillator
Seite 32
5.4 Der quantenmechanische Oszillator
Wie in der klassischen Mechanik betrachten wir zwei Massen, zum Beispiel zwei Atome in einem Molekül. Zwischen den Atomen wirkt hier eine Bindungskraft. (Alles kann im Eindimensionalen betrachtet
werden.) Dieses System vergleichen wir mit einem klassischen Federpendel, bei dem eine Masse m an
der Decke durch eine Feder mit der Federkonstante k aufgehängt ist. Die Gesamtenergie können wir
durch den Hamiltonoperator darstellen:
H=
p2x
m · ω2 2
+
·x
2m
2
Zu den Größen x und px gehören quantenmechanisch die Operatoren X und Px = i~ · ∂/∂x. Wir
definieren nun einen Operator, der gleichzeitig Orts- und Impulsraum addressieren kann:
q
p m·ω
1
a(X, Px ) :=
·
X
+
i
·
2~
2m·ω·~ · Px
q
p m·ω
1
a† (X, Px ) =
2~ · X − i ·
2m·ω·~ · Px
Im Prinzip ist dies das Gleiche vorgehen wie bei der Superposition zweier Zustände. Es ergeben sich
die Relationen:
(a) [a, a† ] = 1
(b) a† a =
m·ω
2~
· X2 +
1
2m·ω·~
· Px2 +
i
2~
· [X, Px ] =
H
~ω
−
1
2
Umgestellt ergibt sich H = ~ · ω · (a† a + 1/2). Man erhält den normierten Hamilton-Operator:
b = H = a† a + 1
H
~ω
2
b ist ein Operator zu den (Energie-)Eigenwerten ε und den Eigenfunktionen |εi,
Angenommen, H
b |εi = ε · |εi.
also gilt H
(c) Kommutatoren:
h
i
£
¤ £
¤
a, a† a + 12 = a, a† a = a
h
i
£
¤
b
a† , H
= a† , a† a + 12 = −a†
b
a, H
=
Nun können a und a† auf die Eigenwerte ε einwirken. Wir wollen zeigen, dass a und a† sinnvolle
Operatoren im Sinne der Quantenmechanik darstellen, welche eine Zustandsänderung erlauben. Dazu
b |εi und Ha
b † |εi.
benutzen wir Operatoren der Ha
h
i
h
i
b
b − Ha
b
b = aH
b − a, H
b
a, H
= aH
⇒ Ha
³
h
i´
³
´
b |εi =
b − a, H
b |εi = aH
b − a |εi = a(H
b − 1) |εi = (ε − 1) · a |εi
Ha
aH
Also hat die Eigenfunktion a |εi einen Eigenwert von ε − 1. Wenn a also auf eine Eigenfunktion |εi
wirkt, wird ε um 1 erniedrigt. Analog folgt:
b † |εi = (ε + 1) · a† |εi
Ha
Die Operatoren a und a† werden Vernichtungs- und Erzeugungsoperator genannt. Nun haben wir
die folgenden Eigenfunktionen:
• Zum Eigenwert ε gehört die Eigenfunktion |εi.
5.4 Der quantenmechanische Oszillator
Seite 33
• Zum Eigenwert ε − 1 gehören die Eigenfunktionen |ε − 1i und a |εi.
• Zum Eigenwert ε + 1 gehören die Eigenfunktionen |ε + 1i und a† |εi.
Da jeder Eigenwert nur eine linear unabhängige Eigenfunktion haben darf, dürfen sich die Eigenfunktionen |ε − 1i und a |εi nur um eine Konstante unterscheiden (analog für ε + 1):
a |εi = Cε |ε − 1i
und
a† |εi = Cε+1 |ε + 1i
Die Abbildungen wirken also so:
a : |εi 7→ |ε − 1i
und
a† : |εi 7→ |ε + 1i
Gibt es einen Grundzustand, also einen tiefsten möglichen Zustand |ε0 i zum Eigenwert ε0 ? Angenommen, |ε0 i existiert. Dann müsste gelten:
a |ε0 i = 0
Umgekehrt kann man den Grundzustand „aus dem Nichts“ erzeugen:
¶
µ
1
†
†
b |ε0 i = 1 |ε0 i
b
|ε0 i ⇒ H
0 = a (a |ε0 i) = a a |ε0 i H −
2
2
Daraus liest man den niedrigsten Eigenwert und die zugehörige minimale Energie des quantenmechanischen Oszillators ab:
1
1
ε0 =
und E0 = ~ · ω
2
2
Da die Eigenwerte sich immer um 1 einterschieden ergibt dich eine Energiedifferenz und damit die
Qunatisierung zu:
∆E = ~ · ω
Diese Quantisierung passt zum Bohrschen Atommodell, zum Planckschen Strahlungsgesetz und zur
Einsteinschen Quantisierung in der Beschreibung des Photoeffektes.
Nun sollen die tatsächlichen Eigenfunktionen bestimmt werden. Dazu werden wir Px = −ih∂/∂x und
X = x in die Operatoren einsetzen:
³
´
r
d
a = √12 · dξ
+ξ
³
´ mit ξ = m · ω · x
d
~
+ξ
a† = √12 · − dξ
Den Operator a wenden wir auf |ε0 i an:
1
0 = a |ε0 i = √ ·
2
!
µ
d
+ξ
dξ
¶
⇒
d
|ε0 i + ξ · |ε0 i = 0
dξ
Hierfür ergibt sich die Lösung für den Grundzustand
µ
¶
³ m · ω ´1/4
1 2
|ε0 i =
· exp − · ξ
π~
2
Die allgemeine Lösung folgt aus wiederholtem Anwenden des Erzeugungsoperators.
µ
¶
³ m · ω ´1/4
1
1
|εn i = √
·
· exp − · ξ 2 · Hn (ξ)
π~
2
2n · n!
Hierbei sind Hn (ξ) die Hermiteschen Polynome.
Bemerkung
zu Abbildung 1.27
5.5 Der Potentialtopf
Seite 34
Betrachten wir den Übergang von |εn i → |un i:
– Grundzustand quantenmechanisch nicht in Ruhe (entgegen der klassischen Physik)
2
– Wahrscheinlichkeitsdichte P (ξ) und |un (ξ)| stimmen für n → ∞ überein, n = 0, 1 bis n ≈ 10 führt
zu einer starken Abweichung.
– Oszillator quantenmechanisch hat diskrete Einergiespektren (entgegen der klassischen Physik)
– Der quantenmechanische Oszillator hat auch außerhalb der Grenzen eine nicht verschwindende
Wahrscheinlichkeitsdichte.
5.5 Der Potentialtopf
Bei der Bindung zwischen Kern und Elektron wirken sowohl die Coulomb-Kraft als auch repulsive
Kernkräfte. Es ergibt sich ein sogenanntes 6-12-Potential:
E(r) ∼ −α ·
1
1
+ β · 12
6
r
r
Solche Potentiale sind sehr schwer zu lösen. Wir wollen als Vereinfachung Potentialtöpfe und Potentialbarrieren betrachten.
5.5.1 Unbegrenzter quadratischer Potentialtopf
Die Lösungen für einen Potentialtopf und einem „Potentialhügel“ sind äquivalent, daher betrachten wir
folgendes Potential:
(
∞ |x| < a (Bereich 1)
V (r) =
0 |x| > a (Bereich 2)
Die Schrödingergleichung im Bereich 1 lautet:
~2 d2 u
·
+E·u=0
2m dx2
Hierbei steckt das Potential im Energieterm. Damit machen wir den Lösungsansatz:
u(x) = A · cos(kx) + B · sin(kx)
Es ergeben sich im Bereich 1 stehende Wellen. Als Randbedingungen nutzen wir, dass u(x) für |x| → ∞
(allgemeiner: im Bereich 2) verschwindet, und, dass die Lösung bei |x| = 0 stetig ist. Es ergeben sich
zwei Lösungsansätze:
1. A · cos(ka) + B · sin(ka) = 0
2. A · cos(ka) − B · sin(ka) = 0
Durch Einsetzen der Randbedingungen ergibt sich für diese Lösungsansätze:
1. B = 0, cos(ka) = 0 und damit k = nπ/2a mit n = 1, 3, 5, . . .
2. A = 0, sin(ka) = 0 und damit k = nπ/2a mit n = 2, 4, 6, . . .
Zusammengefasst erhält man für die Energien und die Eigenfunktionen:

 √1 · cos ¡ nπ·x ¢ n ungerade
2
2
~ π
2a
a
2
·n
und un (x) =
En =
¡
¢
 √1 · sin nπ·x
8ma2
n gerade
2a
a
5.5 Der Potentialtopf
Seite 35
Die verschiedenen Eigenfunktionen weisen eine Parität, also eine Symmetrie, auf. Zudem weisen die
Eigenfunktionen in sich eine Symmetrie auf: Für gerade n sind sie ungerade und umgekehrt:
(
un (x)
n ungerade
un (−x) =
−un (x) n gerade
Aus der Struktur der Lösung entnehmen wir:
• |u1 (x)|2 wird für x = 0 maximal, |u2 (x)|2 wird für x = ±a/2 maximal u.s.w.
• un (±a) = 0 für alle n: Es ist ein sogenanntes hartes Potential.
• Es gibt keine Aufenthaltwahrscheinlichkeit außerhalb der Topfes.
5.5.2 Begrenzter, quadratischer Potentialtopf
Das Potential lautet nun:
V (x) =
(
0
V0
|x| ≤ a
|x| > a
Es ergibt sich wieder eine Schrödingergleichung für |x| > a:
~2 d2 u
·
− (V0 − E) · u = 0
2m dx2
Unser Ansatz für die Eigenfunktionen lautet wieder:
ui (x) ∼ cos(k0 x), sin(k0 x)
Hierbei wird ein neuer Index i (von engl. „incident“ = Einfall) eingeführt. Die Lösungsmethode ist, die
Lösungen links des Potentialtopfes (ul ), im Potentialtopf (ui ), und rechts des Potentialtopfes (ur ) zu
ermitteln, in derselben Reihenfolge, in der die Potentiale bei einem Transmissionsexperiment auf ein
durchfliegendes Teilchen wirken würden. Damit ist k0 = 2m·E/~2 und die ui (x) müssen im Unendlichen
verschwinden. Damit erhalten wir die folgenden Lösungsansätze:
ur (x) = C · e−K·x
und
ul (x) = C 0 · e−K·|x|
Dabei führen wir K 2 = 2m/~2 · (V0 − E) als neue Wellenzahl ein.
1. gerade (posistive) Parität:
ui (x) = A · cos(k0 · x)
⇒
ur (x) = C · e−K·x
und
ul (x) = C 0 · e−K·|x|
2. ungerade (negative) Parität:
ui (x) = A · sin(k0 · x)
⇒
ur (x) = C · e−K·x
und
ul (x) = −C 0 · e−K·|x|
Für beide Lösungen müssen wir die Stetigkeit für die Funktion und ihre Ableitung beachten:
ul/r (±a) = ui (±a)
und
dul/r
dui
(±a) =
(±a)
dx
dx
Zu der Lösung der positiven Parität:
cos(k0 · a) = C · e−K·a
k0 · sin(k0 · a) = KC · e−K·a
¾
⇒
K = k0 · tan(k0 · a)
5.5 Der Potentialtopf
Seite 36
Die Lösung der negativen Parität ergibt:
K = −k0 · cot(k0 · a)
Dies sind transzendente Gleichungen. Es gibt also nur numerische Lösungen für die En . Die Eigenfunktionen folgen dann aus den Lösungen für En . Damit erkennen wir:
• |un (x)|2 6= 0 für x = ±a; Daraus folgt eine endliche Wahrscheinlichkeit für |x| > a.
• Die Eigenfunktionen sind innerhalb des Potentialtopfes ähnlich zum unbegrenzten Potentialtopf.
(Alle paritätischen Erkenntnisse gelten also weiterhin.)
5.5.3 Quantenmechanischer Tunneleffekt
Was geschieht beim Durchgang durch einen rechteckigen, invertierten Potentialtopf (also eine Potentialbarriere)? Dazu haben wir folgendes Beispiel:


x < 0 Bereich 1

0
V (x) =
V0


0
0 < x < s Bereich 2
x > s Bereich 3
(Im Allgemeinen sind Bereich 1 und 3 nicht auf demselben Potential.) Interessant ist jetzt die Frage,
wie sich die Lösungen für E − V0 < 0 und E − V0 > 0 unterscheiden. (Im ersten Fall sagt die klassische
Mechanik voraus, dass die Barriere unüberwindbar ist, da die Aktivierungsenergie nicht ausreicht.) Wir
betrachten nun eine von links einfallende Welle, die an x = 0 entweder reflektiert oder transmittiert
wird. Zwischen 0 < x < s wird das Teilchen im Transmissionsfall weiter propagiert und für x ≥ s
bewegt es sich im Bereich 3 weiter. Wir machen im Bereich 2 den Ansatz:
ui (x) = ui,0 · e±iki ·x
Eine verlustfreie Propagation in ±x-Richtung liegt dann vor, wenn die ki reell sind. Für imaginäre ki
(ki = i · |ki |) ergibt sich:
ui (x) = ui,0 · e±|ki |·x
Hierbei ist nur die Lösung mit Minus physikalisch sinnvoll, sie entspricht einer Dämpfung der Wellenfunktion im Bereich 2. Mit diesen Überlegungen können wir die Lösung für ki interpretieren. Sie lautet
wie folgt:
(
p
p
< 0 ki = ~i · 2m |E − V0 |
2m · (E − V0 )
p
ki =
⇒ E − V0 =
~
> 0 ki = 1 · 2m(E − V0 )
~
Für E −V0 < 0 wird ki imaginär, also ist ui (x) im Bereich 2 exponentiell gedämpft. Im Falle E −V0 > 0
ist ki reell, also oszilliert ui (x) sinusförmig; allerdings verringert sich die Wellenzahl um den Faktor
1 − V0 /E.
Mit den Postulaten von de Broglie erhält man:
r
px
2
=
· (E − v0 )
⇒ vx =
m
m
1. Für E − V0 ≥ 0 entspricht dies einem klassischen Teilchen, das sich im Bereich 2 verlangsamt.
Die Transmissionskoeffizienten steuern bei x = 0:
4E · (E − V0 )
T =
4E · (E − V0 ) + V02 · sin2 (ki · s)
p
px = ~ · ki = 2m · (E − V0 )
Man kann zwei Spezialfälle erzeugen: Es ist T = 0 für E = V0 und T = 1 für ki · s = n · π. Für
alle anderen T liegt eine normale Oszillation vor.
5.6 Auswahlregeln und Übergangsmatrixelemente
Seite 37
2. Für E − V0 < 0 ergibt sich im Bereich 2 eine exponentiell gedämpfte Welle. Daraus ergibt sich
(in Abhängigkeit von s und V0 ) eine verkleinerte Amplitude im Bereich 3.
T =
4E · (V0 − E)
4E · (V0 − E) + V02 · sinh(ki · s)
Die maximale Transmissionsrate („Tunneleffizienz“) ist jetzt:
·
¸−1
V0 · s2
Tmax = 1 +
4
Eine praktische Anwendung finden wir im Tunnelmikroskop: Dort werden Atome detektiert,
indem Elektronen punktuell aus den Atomen abgesaugt werden. Die Aktivierungsenergie eines
Elektrons im Grundzustand ist E = −13,6 eV. Im Allgemeinen entspricht die Barriere der Austrittsarbeit; sie liegt dann im Bereich von etwa 4 bis 5 eV (dieser Wert entspricht gerade dem
V0 aus unserer Rechnung). Um ein einzelnes Elektron aus einem Atom zu ziehen, muss also die
Spitze des Mikroskops sehr nah an das Atom zu bringen. Dabei darf man die Spannung zwischen
Probe und Spitze nicht über 5 V bringen, da sonst der obige Fall 2 in den Fall 1 umschlägt; damit
haben wir kein Tunnelmikroskop mehr, sondern ein Strommessgerät.
5.6 Auswahlregeln und Übergangsmatrixelemente
Bei den Elektronen in einem Atom finden Übergänge zwischen den diskreten Energieniveaus statt. Befindet sich ein Elektron im Zustand |1i, so kann es bei Absorption eines Photons mit einer passenden
Energiemenge in den Zustand |2i übergehen. Das Elektron ist nun angeregt, es wird nach einer gewissen Zeit wieder in den Zustand |1i zurückfallen und dabei ein Photon mit derselben Energiemenge
emittieren (stimulierte Emission).
Um diese Vorgänge rechnerisch zu erfassen, stellen wir uns das Atom im Ursprung eines Koordinatensystems vor. Eine längs der z-Achse linear polarisierte Welle fällt auf das Atom ein (d.h. für das
elektrische Feld und den Wellenzahlvektor: F~ k ~ez und ~k⊥~ez ). Das elektrische Feld kann beschrieben
werden durch:
F~ = F~0 · cos(~k~r − ωt)
Es findet also eine periodische Störung des Potentials des im Atom gebundenen Elektrons statt. Wir
wollen annehmen, dass die Wellenlänge wesentlich größer ist als der Durchmesser des Atoms (damit
kann das elektrische Feld der Welle im Bereich das Atoms als homogen genähert werden). Damit
kommen wir zu der Näherung ~k ·~r = 0 innerhalb des Atoms (welches näherungsweise als komplett im
Koordinatenursprung lokalisiert angesehen werden kann).
Weiterhin nehmen wir das Atom als Ladungsverteilung an, welche insgesamt neutral ist, aber unter
Umständen gibt es ein elektrisches Dipolmoment, Quadrupolmoment, oder ein Moment höherer Stufe.
In einem homogenen Feld liefert aber nur ein Dipolmoment eine Wechselwirkungsenergie. Diese liefert
im Hamiltonoperator einen Störterm:
b = −~
∆H
p · F~ = −ez · F
Es ist ez der elektrische Dipoloperator. Da sich die Elektronen in der Atomhülle bewegen, liegt
zudem eine Stromverteilung vor, es entstehen also magnetische Momente. Im homogenen Feld geht
wiederum nur die Wechselwirkungsenergie des Dipolmoments ein:
b = −~
~
∆H
µ·B
5.6 Auswahlregeln und Übergangsmatrixelemente
Seite 38
Diese Störterme sollen zunächst dimensioniert werden. Typische Größenordnungen für die Momente sind p = e · a0 (mit Bohrschem Atomradius) und µ = µB (das Bohrsche Magneton). Bei der
elektromagnetischen Welle gilt B = F/c. Mit diesen Zusammenhängen ergibt sich µB ¿ pF . Die
Wechselwirkung der elektromagnetischen Welle mit dem elektrischen Dipolmoment dominiert also.
Damit müssen wir im Hamiltonoperator die magnetische Wechselwirkung nicht beachten.
Betrachte zunächst ein Atom in einem ungestörten Eigenzustand, also zum Beispiel |1i mit der zugehörigen Wellenfunktion ψ1 . Der Erwartungswert ist gegeben durch:
Z
Z
∗
hpz i = ψ1 · ez · ψ1 dV = |ψ1 |2 · ez dV = 0
Das Betragsquadrat von ψ1 (x, y, z) ist in z gerade, da das Potential punktsymmetrisch ist. Der Term
ez ist aber offensichtlicherweise ungerade in z, weswegen der Integrand insgesamt ungerade in z ist
und damit das Integral über den gesamten Raum verschwindet. Physikalisch bedeutet das, dass es kein
permanentes Dipolmoment gibt.
Nun befinde sich das Atom in einem Zustand, der einer Überlagerung von |1i und |2i entspricht.
Entsprechend den Überlegungen zur zeitunabhängigen Schrödingergleichung können wir die Wellenfunktion in einem orts- und einen zeitabhängigen Teil aufspalten.
ψ = c1 · ψ1 + c2 · ψ2 = c1 · u1 (~r) · e−i·
E1 t
~
+ c2 · u2 (~r) · e−i·
E2 t
~
Jetzt ergibt sich:
|c2 · u2 |2 · ez dV
R
R
(E1 −E2 )t
(E2 −E1 )t
+
c1 c∗2 · u∗2 · ez · u1 · e−i ~
dV + c∗1 c2 · u∗1 · ez · u2 · e−i ~
dV
hpz i =
R
|c1 · u1 |2 · ez dV +
R
Die ersten beiden Terme verschwinden
R ∗ aufgrund derselben Überlegungen wie oben. Zur Vereinfachung
führen wir die Abkürzung p12 = u1 · ez · u2 dV ein. Es verbleibt:
h
i
(E2 −E1 )t
hpz i = 2 Re c∗1 c2 · p12 · e−i ~
Falls p12 6= 0, dann hat die Superposition von |1i und |2i ein elektrisches Dipolmoment, welches mit
der Kreisfrequenz (E2 − E1 )/~ oszilliert. Diese Frequenz heißt Übergangsfrequenz. Die Wechselwirkung mit der elektromagnetischen Welle ist dann maximal (resonant), wenn die Welle ebenfalls diese
Kreisfrequenz hat. Das Dipolmoment p12 bezeichnet man als Übergangsdipolmatrixelement. Ein
elektrischer Dipolübergang zwischen |1i und |2i ist genau dann möglich, wenn p12 6= 0 ist.
Die Frage nach den Werten für die Quantenzahlen von |1i und |2i, bei denen ein Übergang stattfinden
kann, führt uns auf die Auswahlregeln. Betrachte dazu die Wasserstoff-Eigenfunktionen. Im H-Atom
kann der ortsabhängige Teil u(~r) der Wellenfunktion in einem Radialteil, einen Azimutalteil und einen
Polarteil zerlegt werden. Der Erwartungswert hpz i berechnet sich dann wie folgt:
h
i∗
h
i
R2π Rπ
R∞
|m |
|m2 |
−im2 ϕ
ϑ
dϕ sin ϑdϑ r2 dr Rn1 ,l1 (r) · Pl1 1 (cos ϑ) · e−im1 ϕ · e |r cos
·
R
(r)
·
P
(cos
ϑ)
·
e
n2 ,l2
l2
{z }
0
0
0
=z
=
e·
·∞
R
0
Rn∗ 1 ,l1 (r)
r3
· Rn2 ,l2 (r) ·
¸ ·π
¸ · 2π
¸
R |m1 |
R i(m −m )·ϕ
|m2 |
1
2
dr ·
Pl1 (cos ϑ) · Pl2 (cos ϑ) · cos ϑ sin ϑ dϑ ·
e
dϕ
0
0
Alle Integrale müssen ungleich Null sein, damit p12 nicht Null wird. Aus dem Integral über ϕ lesen
wir ab, dass m1 = m2 sein muss. Für das Integral über ϑ verwenden wir die folgende Rechenregel für
Legendre-Polynome:
|m1 |
(2l + 1) · cos ϑ · Pl
|m |
|m |
(cos ϑ) = (l − |m| + 1) · Pl+11 (cos ϑ) + (l + |m|) · Pl−11 (cos ϑ)
5.6 Auswahlregeln und Übergangsmatrixelemente
Seite 39
Damit wird das Integral über ϑ nach Substitution zu:
l2 − |m2 | + 1
·
2l2 + 1
Z1
|m |
|m2 |
Pl1 1 (cos ϑ) · Pl2 +1
(cos ϑ)
−1
l2 + |m2 |
·
d(cos ϑ) +
2l2 + 1
Z1
|m1 |
Pl1
|m |
2
(cos ϑ) · Pl2 −1
(cos ϑ) d(cos ϑ)
−1
Für m1 = m2 enthalten die Integrale Produkte von zwei assozierten Legendre-Polynomen zu gleichem
m, aber unterschiedlichem l. Die assoziierten Legendre-Polynome sind aber bei Integration orthogo|m |
|m2 |
nal: Pl1 1 ⊥Pl2 ±1
, also verschwindet der gesamte Term außer für l1 = l2 ± 1. Insgesamt haben wir
gefunden:
∆m = 0 und ∆l = ±1
Neben p12 , genauer: p12z , können wir auch die anderen Komponenten des Dipolmomentes betrachten,
bzw. die entsprechenden Übergangsdipolmatrixelemente p12x und p12y .
hp12x i = e · hun1 ,l1 ,m1 | x |un2 ,l2 ,m2 i
mit
x = r sin ϑ cos ϕ = r sin ϑ ·
eiϕ + e−iϕ
2
Es ergeben sich wieder drei Integrale für die drei Polarkoordinaten. Das Integral über ϕ sieht so aus:
Z ³
´
1
ei(m1 −m2 +1)·ϕ + ei(m1 −m2 −1)·ϕ dϕ
·
2
Hieraus entstehen neue Auswahlregeln:
∆m = ±1 und ∆l = ±1
Eine analoge Betrachtung bei p12y (mit y = r sin ϑ sin ϕ = r sin ϑ · (exp(iϕ) − exp(−iϕ))/2i) ergibt
dieselben Auswahlregeln, aber mit einem kleinen Unterschied in den Formeln:
∆m = m2 − m1 = +1 ⇒ p12y = −i · p12x
∆m = m2 − m1 = −1 ⇒ p12y = +i · p12x
Die x- und y-Komponenten sind um ±π/2 gegeneinander phasenverschoben. Das Dipolmoment rotiert
also in der xy-Ebene. Übergänge mit ∆m = ±1 bezeichnet man als σ-Übergänge, bei ∆m = 0 liegt
ein π-Übergang vor. Ein π-Übergang wird von längs der z-Achse linear polarisiertem Licht induziert
(~k⊥~ez ); σ-Übergänge treten bei Einfall von in der xy-Ebene polarisiertem Licht auf (~k k ~ez ). Nach
dem Superpositionsprinzip sind natürlich auch Kombinationen mehrerer Übergänge möglich. Für ein
unpolarisiertes und isotropes Lichtfeld gilt die Auswahlregel: ∆l = ±1 und ∆m = −1, 0, 1. (Es sind
alle Polarisierungsarten im einfallenden Licht enthalten.)
Erweiterte Auswahlregeln
Bei erweiterten Auswahlregeln werden zusätzlich die Fein- und Hyperfeinstruktur berücksichtigt.
Übergänge zwischen...
Feinstruktur-Niveaus
Hyperfeinstruktur-Niveaus
Mögliche Zustandsänderung
∆j = −1, 0, 1 ∆l = ±1 ∆mj = −1, 0, 1
∆f = −1, 0, 1 ∆l = ±1 ∆mf = −1, 0, 1
Auszuschließen sind: j = 0 nach j = 0 und f = 0 nach f = 0.
5.7 Zweiniveausysteme. Einstein-Koeffizienten. Laser
Seite 40
Wechselwirkungen höherer Ordnung
~
Wir haben eine Welle: F~ = F~0 · ei(k~r−ωt und entwickeln diese um ~r = 0.
1
~
eik·~r = 1 + i~k ·~r − · (~k ·~r)2 + . . .
2
Bisher hatten wir diese Entwicklung nach dem konstanten Glied abgebrochen. Die zusätzlichen Terme
führen zu Wechelwirkungen auch mit höheren Momenten wie Quadrupolen, Oktopolen und so weiter.
Damit ergeben sich auch andere Auswahlregeln. Als Bezeichnungen vereinbaren wir:
Bezeichnung
E1
E2
E3
berücksichtigt...
elektrischer Dipolübergang
elektrischer Quadrupolübergang
···
Für die magnetischen Übergänge wählt man analog M1, M2, M3 und so weiter.
5.7 Zweiniveausysteme. Einstein-Koeffizienten. Laser
Einstein hatte 1924 die Idee, die Übergänge zwischen Energieniveaus |1i und |2i an die Planck’sche
Hohlraumstrahlung zu koppeln. Damit erklärte er die fundamentalen Prozesse im Zweiniveausystem,
also Absorption und Emission. Zum anderen hatte Einstein erkannt, dass die Wahrscheinlichkeit des
Übergangs von der Besetzung der Niveaus abhängig ist. Ein Niveau |ni verfügt neben dem Energieeigenwert En auch über eine mittlere Verweildauer τn .
Für die Berechnung nehmen wir an, dass die Anzahl der Elektronen im Atom konstant ist. Prinzipiell
ist zur Lösung die Quantenelektrodynamik, insbesondere die Quantisierung des äußeren Feldes, nötig.
Daraus retten wir uns, indem wir ein Ensemble mehrerer Elektronen betrachten.
Ein Laser besteht prinzipiell aus einem Medium (beliebigen Aggregatzustandes), welches einer Punktstrahlung aus einer externen Quelle ausgesetzt ist. Die Photonen dieser Strahlung tragen die Energie:
Ep = ~ · νp =
~c
λp
Die Energie der emittierten Photonen ist:
Ee = ~ · νe =
~c
λe
Atome-LaserAufbau
5.7 Zweiniveausysteme. Einstein-Koeffizienten. Laser
Seite 41
Insgesamt muss natürlich der Enerigeerhaltungssatz und der Impulserhaltungssatz gelten. Man stellt fest, dass die Absorptionsrate abhängig
von der Wellenlänge der Punktstrahlung ist, sie wird maximal für ein λp,0 .
Die Emission ergibt ein kontinuierliches Spektrum, die Emissionsrate hat
ebenfalls ein Maximum, dass mit λe,0 bezeichnet wird.
Um den Photonenstrahl mehrmals zu verstärken, bringt man links und
rechts vom Medium Spiegel an. Diese Spiegel S1 und S2 bilden eine Kavität, sie geben also eine Vorzugsrichtung an. Um das System als Lichtquelle nutzen zu können, wird einer der Spiegel (in unserem Falle S2 )
teilweise durchlässig gemacht, der Reflexionskoeffizient ist also R < 1.
Im Laser geht allerdings viel Energie verloren durch:
Atome-LaserAbsorptionEmission
• Wärme
• Absorption
• räumliche Anisotropie, Kavität
Insgesamt liegt die Effizienz eines Lasers (also sein Wirkungsgrad) nur bei ungefähr 1 bis 2%.
Im Laser gibt es (für zwei Zustände |1i und |2i mit E1 < E2 ) drei fundamentale Übergänge:
1. Absorption: Ein Photon der Energie hν = E2 − E1 wird absorbiert. Das Elektron geht vom
Zustand |1i in |2i über, wo es für die Zeit τ2 verweilen kann. Nach Einstein ist die Übergangsrate
B12 · %(ν), wobei B12 der entsprechende Einstein-Koeffizient und %(ν) die Frequenzverteilung
des Planckschen Hohlraumstrahlers ist:
%(ν) =
8π · ν 3
1
· ~ν/kT
3
c
e
−1
2. Stimulierte Emission: Ein Photon der Energie hν fällt ein, regt das angeregte Elektron ab, d.h. es
verursacht den Übergang vom Zustand |2i zu |1i. Dabei entsteht ein weiteres Photon, welches mit
dem ersten für alle Zeiten in Phase sind. Das heißt, man erhält kohärente Wellen. Die Energien
lauten −hν = E1 − E2 und hν = E2 − E1 . Die Übergangsrate ist B21 · %(ν) mit dem EinsteinKoeffizient B21 der stimulierten Emission.
3. Spontane Emission: Nach der Lebensdauer τ2 „zerfällt“ der Zustand |2i zu |1i. Die Übergangsrate
A21 ist der Einstein-Koeffizient der spontanen Emission.
Die Betrachtung mit der Quantenelektrodynamik ist nicht notwendig, denn:
1. Es wird über viele Übergänge gemittelt (da man es mit einem Elektronenensemble zu tun hat).
2. Die Elektronen wechselwirken nicht mit dem äußeren elektrischen Feld.
Die Einstein-Koeffizienten sollen nun quantifiziert werden. Wir nehmen an, dass sich auf dem unteren
Niveau |1i genau N1 Elektronen befinden, während N2 Elektronen im Zustand |2i verweilen. Diese
Anzahlen ändern sich bei allen Übergängen; mithilfe der bekannten Übergangsraten kann man Ratengleichungen aufstellen, die die Bevölkerung und Entvölkerung der einzelnen Niveaus beschreiben:
dN1
= −B12 · %(ν) · N1 + A21 · N2 + B12 · %(ν) · N2
dt
Der erste Summand ist die Entvölkerung von |1i. Der zweite Summand kommt von der spontanen
Emission und der dritte aus der stimulierten Emission. Beide entsprechen einer Bevölkerung von |1i.
Analog bei dem Niveau 2:
dN2
= B12 · %(ν) · N1 − A21 · N2 − B21 · %(ν) · N2
dt
5.7 Zweiniveausysteme. Einstein-Koeffizienten. Laser
Seite 42
Im thermischen Gleichgewicht muss gelten:
dN1
dN2
=−
dt
dt
⇒
d
(N1 + N2 ) = 0
dt
⇔
N1 + N2 = const.
Das heißt, dass die totale Anzahl der Elektronen konstant bleiben muss. Wir betrachten nun den
stationären Zustand, in welchem beide Zeitableitungen verschwinden. Dann folgt:
N1 · B12 · %(ν) = N2 · (A21 + B21 · %(ν))
⇒
N2
B12 · %(ν)
Wabs
=
=
N1
A21 + B21 · %(ν)
Wem
(∗)
Es ist Wabs die Wahrscheinlichkeit für die Absorption von Photonen und Wem entsprechend die Wahrscheinlichkeit der Emission von Photonen. Das Verhältnis N2 /N1 ist Boltzmann-verteilt:
N2
g2 − ~ν
=
· e kT
N1
g1
(∗∗)
Da mehrere Elektronen auf einem Zustand liegen können, haben wir eine Entartung der Elektronen
gefordert. Die Faktoren g1 und g2 quantifizieren die Entartung der Zustände |1i und |2i und stellen
eine notwendige Korrektur dar, da (wie wir bald sehen werden) eigentlich nicht alle
Mit einem Koeffizientevergleich aus den beiden Gleichungen (∗) und (∗∗) erhalten wir:
B12 = B21 ·
g2
g1
und A21 =
8π·ν 3
c3
· B21
A und B sind die entsprechenden Einsteinkoeffizienten, die die quantitativen Übergangsraten der drei
fundamentalen Übergangsprozesse beschreiben. Betrachten wir nun in z-Richtung linear polarisiertes
Licht und den Dipolübergang. Dann sind die Übergangsraten:
Tabs = B12 · %(ν) =
2e2 π 2
· |hu2 | z |u1 i|2 · %(ν)
ε0 · h2
Im Dreidimensionalen (d.h. wenn die Polarisierungsrichtung des Lichtes nicht bekannt ist):
Tabs = B12 · %(ν) =
2e2 π 2
· |hu2 |~r |u1 i|2 · %(ν)
3 · ε0 · h 2
Analog können wir die Übergangsraten auch für die Emission formulieren:
Temm = A21 =
16e2 π 2
· ν 3 · |hu2 |~r |u1 i|2
3ε0 · hc2
Dieser Term soll weiter abgeschätzt werden:
hu2 |~r |u1 i ≈ a0
⇒
A21 ≈
16π 2 · e2 · a20 · ν 3
3ε0 · hc2
Hierbei ist a0 der Bohrsche Radius. Typische Werte sind A21 ≈ 108 s−1 , entsprechend einer Lebensdauer von τ2 = A121 = 10−8 s.
Diese neuen Betrachtungen der Quantentheorie eignen sich sehr gut für:
• Energieniveauschemata
• Lebensdauer von Zuständen
• Übergangswahrscheinlichkeiten und -intensitäten
5.7 Zweiniveausysteme. Einstein-Koeffizienten. Laser
Seite 43
• Spektrallinien
Weiterhin gibt es noch die Matrixdarstellung für die Heisenbergsche Quantentheorie.
In der Praxis sind Zweiniveausysteme schlecht, man nimmt meist Vierniveausysteme mit einem stabilen Zustand |0i, zwei instabilen Zuständen |1i und |2i sowie einem metastabilen Zustand |3i. Durch
Einwirkung von außen wird von |0i nach |3i gepumpt, der Zustand zerfällt dann schrittweise. Der
eigentlich genutzte Übergang ist der von |2i nach |1i. Vierniveausysteme realisiert man durch Mischen
mehrerer Stoffe, da die Elektronen auch zwischen verschiedenen Atomen wechseln können.
6.2 LS-Kopplung und jj-Kopplung
Seite 44
6 Atomstrukturen mit mehreren
Elektronen
Bisher hatten wir nur das H-Atom oder ähnliche Atome mit genau einem Elektron betrachtet. Jetzt
wollen wir das Vielteilchenproblem lösen, dass sich beim Vorhandensein mehrerer Elektronen ergibt. Da
dieses System selbst bei zwei Teilchen sehr kompliziert sind, müssen wir Näherungsverfahren anwenden.
Wir erhalten neue quantenmechanischen Effekte, wie zum Beispiel Wechselwirkungen und Spin-BahnKopplungen zwischen verschiedenen Elektronen.
Daraus ergeben sich die Folgerungen:
• Die einzelnen Elektronen sind unterscheidbar.
• Energieniveaus können aufgefüllt werden.
• Pauli-Prinzip: Antisymmetrische Wellenfunktionen spielen eine entscheidene Rolle.
• Die Struktur des Periodensystems kann vollständig erklärt werden.
• Diese Theorien bilden die Grundlage der Festkörperphysik und der Molekülphysik.
6.1 Die elektrostatische Korrelation
Wir beginnen analog zum Einteilchensystem mit der Grobstruktur. Dazu betrachten wir ein Atom
(Ladung Z · e) im Koordinatenursprung eines dreidimensionalen Raumes, um das sich Z Elektronen
(mit den Ortsvektoren ~ri ) bewegen. Der Abstand zweier Elektronen ist ~rij = ~ri −~rj . Natürlich wirkt
sich die Konstellation auf den Hamiltonoperator aus:
¶ X
z µ
z
X
~2 ~ 2
Ze2
e2
H=
−
· ∇i −
+
2m
4πε0 · ri
4π · ε0 · rij
i=1
i<j
Im ersten Term wird über alle Elektronen e− summiert. Im zweiten Term (∗) wird die Korrelation
(Wechselwirkung) zwischen den Elektronen betrachtet. Im Allgemeinen ist die Lösung von (∗) sehr
schwierig, deshalb betrachtet man zwei Spezialfälle:
1. Der Wechselwirkungsterm wird groß.
2. Der Wechselwirkungsterm wird klein.
6.2 LS-Kopplung und jj-Kopplung
Wir betrachten den ersten Fall:
z
X
i<j
X
e2
À
C · (~li · ~si )
4π · ε0 · rij
i
6.3 Pauli-Prinzip. Symmetrie von Wellenfunktionen
Seite 45
Hierbei sind ~li und ~si der Bahn- und der Spindrehimpuls des i-ten Elektrons. C ist eine Konstante. Daraus folgern wir, dass die Kopplung im einzelnen Elektron (also die Kopplung von ~li mit ~si )
~ und
aufgebrochen wird. Die Folge ist, dass alle ~li und alle ~si zu einem globalen Bahndrehimpuls L
~
einem globalen Spindrehimpuls S zusammenkoppeln. Es ergibt sich auch ein neuer Gesamtdrehimpuls
~ + S,
~ um welchen L
~ und S
~ (mit verschiedenen Frequenzen!) präzedieren.
J~ = L
Starke Korrelation führt also zu LS-Kopplung. Dieser Fall ist wichtig für leichte Atome und kann zum
Beispiel mit Kernspinresonanz-Spektroskopie quantifiziert werden.
Nun betrachten wir den zweiten Fall:
z
X
i<j
X
e2
¿
C · (~li · ~si )
4π · ε0 · rij
i
In guter Näherung bewegt sich jedes Elektron mit seiner ~li -~si -Kopplung in einem mittleren Zentralfeld.
Im Gegensatz zum ersten Fall ergibt sich ein globaler Gesamtdrehimpuls aus den Gesamtdrehimpulsen
der einzelnen Elektronen:
X
X
~ji =
(~li + ~si )
J~ =
i
i
~ Man erhält also eine jj-Kopplung mit:
Die einzelnen ~ji präzedieren um J.
~ jj ≈
H
X
C · ~li · ~si
i
Schwache Korrelation führt zu jj-Kopplung, was besonders bei schweren Atomen relevant ist.
6.3 Pauli-Prinzip. Symmetrie von Wellenfunktionen
Im Jahre 1924 wurde von Wolfgang Pauli das Pauli-Prinzip für den Ausschluss von Elektronen
formuliert. Es lautet:
Zwei Elektronen im Zentralfeld des Atomkerns können nicht in demselben Zustand sein. Ein Zustand wird durch einen der folgenden
Sätze von Quantenzahlen beschrieben:
• n, l, ml und s
• n, l, j und mj
Pauli-Prinzip
Die Umsetzung des Pauli-Prinzips erfolgt durch Heisenberg und Dirac als Symmetrieforderung an
die Wellenfunktion. Anschaulich kann man sich das Pauli-Prinzip so vorstellen: Angenommen, zwei
Elektronen wären nicht unterscheidbar (d.h. sie haben dieselben Quantenzahlen). Die zugehörige Wechselwirkungsenergie ergibt sich aus dem Hamilton-Operator H(1, 2), der die Wechselwirkung zwischen
dem Teilchen 1 und dem Teilchen 2 beschreibt. Da die Teilchen nicht unterscheidbar sind, kann man
1 und 2 vertauschen: H(1, 2) = H(2, 1). Zu den Hamilton-Operatoren gehören zwei Wellenfunktionen
ψ(1, 2) und ψ(2, 1). Nun definieren wir einen Austauschoperator P12 , der die Teilchen 1 und 2 vertauscht. Auf den Hamilton-Operator, die resultierende Wellenfunktion und die Schrödingergleichung
6.4 Die Struktur des He-Atoms
Seite 46
wirkt der Operator also wie folgt:
P12 [H(1, 2)]
P12 [ψ(1, 2)]
P21 [H(1, 2)ψ(1, 2)]
⇒ 0
0
=
=
=
=
=
H(2, 1)
ψ(2, 1)
H(2, 1) · ψ(2, 1) = H(1, 2) · P12 ψ(1, 2)
P12 H(1, 2) · ψ(1, 2) − H(1, 2)P12 · ψ(1, 2)
[P12 , H(1, 2)]
P12 und H(1, 2) haben einen gemeinsamen Satz von Eigenfunktionen. Diese Eigenfunktionen sind also
ψ(1, 2) mit den Eigenwerten E bezüglich dem Hamiltonoperator. Es muss eine analoge Schrödingergleichung mit dem noch nicht bekannten Eigenwert p für P12 gelten:
P12 ψ(1, 2) = p · ψ(1, 2)
Wir wissen aber:
!
P12 ψ(1, 2) = ψ(2, 1) = p · ψ(1, 2)
Analog wäre (wenn man die Indizes anders nennt):
!
P21 ψ(2, 1) = ψ(1, 2) = p · ψ(2, 1)
und
P12 ψ(2, 1) = ψ(1, 2) = p2 · ψ(1, 2)
Die Eigenwerte zu P12 können also nur 1 oder −1 sein, damit ist:
ψ(1, 2) = ±ψ(2, 1)
Folgerungen:
• Jede akzeptable Wellenfunktion ψ, die zwei Teilchen beschreibt, muss entweder symmetrisch oder
antisymmetrisch sein.
• Diese Eigenschaft kann auf N Teilchen übertragen werden: ψ(1, . . . , N )
• Es existieren zwei Klassen von Teilchen in der Natur:
– Für p = 1 liegen Bosonen vor. Hier sind die Wellenfunktionen symmetrisch, und der
Gesamtspin muss immer ganzzahlig sein. Wichtige Beispiele sind α-Teilchen und Pionen
(S = 0) oder Deuteronen (S = 1).
– Für p = −1 hat man Fermionen, bei denen die Wellenfunktionen antisymmetrisch und der
Gesamtspin halbzahlig ist. Bekannte Beispiele sind Elektronen, Protonen und Neutronen
(S = 1/2) oder Neutrinos.
• Die Potentiale V (r) sind unabhängig vom Teilchenaustausch; daher können wir einen allgemeinen
Ansatz für die Wellenfunktion machen:
i
1 h
ψ(1, 2) = √ · u1 (1) · u2 (2) ± u1 (2) · u2 (1)
2
Hierbei sind u1 und u2 die Wellenfunktionen der einzelnen Teilchen. Das Plus gilt für Bosonen,
das Minus für Fermionen. Ein Spezialfall ist u1 = u2 : Bei Fermionen verschwindet die Wellenfunkion. Hiermit haben wir eine quantenmechanische Formulierung des Pauli-Prinzips (anhand
symmetrischer und antisymmetrischer Wellenfunktionen).
• Diese Beschreibung der Wellenfunktionen ist ausreichend für das Auffüllen der Energieniveaus
im Periodensystem.
6.4 Die Struktur des He-Atoms
Seite 47
6.4 Die Struktur des He-Atoms
Wir betrachten ein Zweielektronensystem (also Z = 2), für das keine LS-Kopplung vorliegt, und
betrachten die Grobstruktur. Der Hamiltonoperator lautet:
~2 ~ 2
Ze2
e2
~2 ~ 2
Ze2
0
H=−
−
+
= H0 + β · H
· ∇1 −
· ∇2 −
2m
2m
4πε0 · r1 4πε0 · r2 4π · ε0 · r12
|
{z
} |
{z
}
=H 0
=β·H
0
Für den Fall, dass β = 0 ist, haben wir ein wasserstoffartiges Atom. Der Lösungsansatz ist dann eine
Produktfunktion u1 (~r1 ) · u2 (~r2 ), wobei jedes ui (~ri ) die folgende Gleichung erfüllt:
−
Ze2
~2 ~ 2
· ui (~ri ) = Ei · ui (~ri )
∇i ui (~ri ) −
2m
4πε0 · ri
Hieraus sieht man, dass auch die Eigenwerte wasserstoffartig sind. Die Gesamtenergie ergibt sich aus der
Überlagerung: Etot = E1 + E2 . Die Eigenfunktionen haben voneinander unabhängige Quantenzahlen
n1 und l1 sowie n2 und l2 . Der Fall n1 = n2 und l1 = l2 ist zugelassen, was ein Widerspruch zum
Pauli-Prinzip ist. Der Term (∗) kann also nicht vernachlässigt werden.
Im Folgenden ist β ein Gewichtungsfaktor, für den β ¿ 1 gilt, also ist auch β · H 0 ¿ H0 . Solche
kleinen Störungen approximiert man für gewöhnlich durch lineare Funktion, analog dazu können wir
einen neuen Lösungsansatz als Linearkombination der ungestörten Eigenfunktionen formulieren. Diese
Eigenfunktionen ergeben sich aus:
H 0 u0n = E0n · u0n
Hierbei sind die u0n also die Lösungen für die Eigenfunktionen für den Fall β = 0. Diese Lösungen
bilden eine vollständige Orthonormalbasis. Gesucht sind aber eigentlich die Lösungen un des gestörten
Problems, für die gilt:
Hun = En · un
Wir machen einen Ansatz für das gestörte Problem:
Eigenwerte: En = E0n + β · E1n + β 2 · E2n + . . .
Eigenfunktionen: un = u0n + β · u1n + β 2 · u2n + . . .
Darin sind allerdings nur E0n und u0n bekannt. Den Ansatz setzen wir in das Eigenwertproblem ein:
0
(H 0 + β · H ) · (u0n + β · u1n + . . .) = (E0n + β · E1n + . . .) · (u0n + β · u1n + . . .)
Beim Koeffizientenvergleich der Potenzen von β:
βn, n = 0 :
H 0 · u0n = E0n · u0n
0
n
β , n = 1 : H 0 · u1n + H · u0n = E0n · u0n + E1n · u0n
0
β n , n = 2 : H 0 · u2n + H · u1n = E0n · u0n + E1n · u1n + E2n · u0n
Hiermit haben wir eine Rekursionsformel, mit der wir aus den bekannten E0n und u0n auf die Ekn und
ukn schließen können. Jeder Schritt ergibt eine höhere Ordnung der Störungsrechnung. Wie viele Ordnungen man berechnen muss, hängt von der Anwendung ab. Zur Quantifizierung der ersten Ordnung
machen wir einen Ansatz, der die ähnliche Position der E0n und E1n bzw. u0n und u1n in der Formel
berücksichtigt.
X
u1n =
ank · u0k
k
6.4 Die Struktur des He-Atoms
Einsetzen in die obige Rekursionsformel ergibt:
X
0
ank · (E0n − E0k ) · u0k
(H − E1n )u0n =
Seite 48
(∗∗)
k
Dieser Term wird wie folgt umgeformt:
1. Multiplikation von links mit u∗0n führt links zum Erwartungswert hH 0 i = h u∗0n | H 0 u0n i
2. Integration über dΩ
3. Ausnutzung der Orthonormiertheit der u0k
Wir erhalten die Eigenwerte:
E1n =
0
Hnn
D
= H
0
E
Z
=
0
u∗0n · H u0n dΩ
Um die Eigenfunktionen zu erhalten, nehmen wir stattdessen folgende Umformung vor:
1. Multiplikation mit u0m (n 6= m)
2. Integration über dΩ
3. Ausnutzung der Orthonormiertheit der u0k
Damit ergeben sich die Koeffizienten zu:
amn
0
Hmn
=
E0n − E0m
für
n 6= m
mit
0
Hmn
D E Z
0
0
= H = u∗0m · H u0n dΩ
Somit gilt für die Eigenfunktionen:
un = u0n +
X
k6=n
0
Hkn
· u0k + . . .
E0n − E0k
Für die zweite Ordnung machen wir einen ähnlichen Ansatz:
X
X
u2n =
bnk · u0k ⇒ E2n =
k
k6=n
0 |2
|Hkn
E0n − E0k
Wir sehen, dass die Störungsrechnung, also die lineare Entwicklung nach bekannten Lösungen, in
b 0 führt auf eine Energiekorrektur:
diesem Falle ein probates Mittel ist. Der Störungsoperator H
Z
D
E
e2
b0 =
b 0 ψ(1, 2) dΩ = ψ(1, 2) | H
b 0 ψ(1, 2)
H
⇒ ∆E = ψ ∗ (1, 2) · H
4π · ε0 · rij
Die Struktur von ψ(1, 2) enthält die folgenden Eigenschaften:
• Antisymmetrie
• Der Elektronen-Spin wird berücksichtigt, hier mit der LS-Kopplung:
~ s1 und e− : ~l2 , ~s2
e−
1 : l1 , ~
2
⇒
~ =~l1 + ~l2 und S
~ = ~s1 + ~s2
L
• Die z-Komponenten des Spins können verschiedene Zustände:
~ =0
|S|
~ =1
|S|
⇒ ms = ms1 + ms2 = 
0


1
⇒ ms = ms1 + ms2 =
0


−1
Es gibt also vier mögliche Eigenfunktionen ψ(1, 2), nämlich einen Singulett-Zustand und drei
Triplett-Zustände.
6.4 Die Struktur des He-Atoms
Seite 49
Wie kann der Spin in den Eigenfunktionen berücksichtigt werden? Dazu führen wir Spinfunktionen
α(i) und β(i), die sogenannten Spinoren, ein:
ui (~ri ) · α(i)
und
ui (~ri ) · β(i)
Den Spinor α(i) benutzt man im Falle ~si · ~ez , während β(i) die Situation ~si · −~ez beschreibt. Jedes
Energieniveau kann beide Einstellungen einnehmen, man schreibt die erste als » und die zweite als º.
Wenn man das Pauli-Prinzip beachtet ergeben sich vier Möglichkeiten für die Kombinationen:
(a) Triplettfunktion mit ms = +1: Zustand »»
´
1 ³
T
√
ψm
=
·
u
(~
r
)
·
u
(~
r
)
−
u
(~
r
)
·
u
(~
r
)
· α(1) · α(2)
1
1
2
2
1
2
2
1
s =+1
2
(b) Triplettfunktion mit ms = −1: Zustand ºº
´
1 ³
T
√
ψm
=
·
u
(~
r
)
·
u
(~
r
)
−
u
(~
r
)
·
u
(~
r
)
· β(1) · β(2)
1
1
2
2
1
2
2
1
s =−1
2
(c) Triplettfunktion mit ms = 0: Zustand »» + ºº
´ ³
´
1 ³
T
√
·
u
(~
r
)
·
u
(~
r
)
−
u
(~
r
)
·
u
(~
r
)
·
α(1)
·
β(2)
+
α(2)
·
β(1)
ψm
=
1
1
2
2
1
2
2
1
s =0
2
(d) Singulettfunktion mit ms = 0: Zustand »» − ºº
´ ³
´
1 ³
S
√
=
·
u
(~
r
)
·
u
(~
r
)
+
u
(~
r
)
·
u
(~
r
)
·
α(1)
·
β(2)
−
α(2)
·
β(1)
ψm
1
1
2
2
1
2
2
1
s =0
2
Die Funktionen a) bis c) sind antisymmetrisch in der Ortsfunktion, die Funktion d ist hingegen antisymmetrisch im Spinor. Wie sehen die Energieeigenwerte aus?
s 1
e2
S
S∗
∆E S = 4πε
·
r12 · ψ0 · ψ0 dΩ1 dΩ2
0
³
´ ³
´
∗
∗
∗
∗
u
(~
r
)
·
u
(~
r
)
+
u
(~
r
)
·
u
(~
r
)
·
u
(~
r
)
·
u
(~
r
)
+
u
(~
r
)
+
u
(~
r
)
1
1
2
2
1
2
2
1
1
2
2
1
s
1
2
1
2
e2
= 4πε
·
dΩ1 dΩ2
r12
0
Die Spinfunktionen α(i) und β(i) sind normiert und tragen daher nichts zur Energie bei. Die Energieänderung ∆E S = J + K besteht aus zwei Teilen mit:
³
´
∗ (~r ) · u (~r ) · u∗ (~r ) + u (~r ) · u∗ (~r ) · u (~r ) · u∗ (~r )
x
u
(~
r
)
·
u
2
1
1
1
2
2
2
1
2
2
2
1
1
1
2
1
2
e
·
dΩ1 dΩ2
J=
4π · ε0
r12
−
Der Term J beschreibt eine reine Coulomb-Wechselwirkung zwischen e−
1 und e2 . Der erste Summand
enthält die Wechselwirkung 1 ↔ 2 an deren Positionen ~r1 und ~r2 , der zweite Summand ist dieselbe
Wechselwirkung, aber mit vertauschten Orten.
³
´
∗ (~r ) · u (~r ) · u∗ (~r ) + u (~r ) · u∗ (~r ) · u (~r ) · u∗ (~r )
x
u
(~
r
)
·
u
2
1
2
2
2
1
1
1
2
2
2
1
1
1
2
2
1
e
K=
·
dΩ1 dΩ2
4π · ε0
r12
Dies ist der Heisenberg-Term, der wahrscheinlich Austauschenergien beschreibt. (Die exakte Bedeutung ist noch unklar.) Im Singulettzustand ergibt sich nun eine totale Energie:
6.4 Die Struktur des He-Atoms
Seite 50
E S = E1 + E2 + ∆E S = E1 + E2 + J + K
Energie im Singulettzustand
Hierbei ist E1 + E2 = −27,2 eV (die doppelte Energie des Elektrons im Grundzustand des H-Atomes).
Im Triplettzustand ergibt sich eine andere Energieänderung:
∆E T =
´ ³
´
x³
e2
·
u1 (~r1 ) · u2 (~r2 ) − u1 (~r2 ) · u2 (~r1 ) · u∗1 (~r1 ) · u∗2 (~r2 ) − u∗1 (~r2 ) + u∗2 (~r1 ) dΩ1 dΩ2
2 · 4π · ε0
Es ist gerade E T = J − K, somit ist die gesamte Energie im Triplettzustand:
E T = E1 + E2 + J − K
Energie im Triplettzustand
Wir sehen, dass E T < E S sein muss. Aus einem Termschema (Abb 1.36) des Heliumatoms entnehmen
wir aufgrund der Energiedifferenz der 2s-Zustände für Singulett (Para-Helium) und Triplett (OrthoHelium) 2 · K ≈ 0,8 eV.
Weitere Zustände durch Spin-Bahn-Kopplung: Russel-Saundes-Kopplung (für leichte Atom wie He).
~ = 0) ist s1 + s2 = 0 und L
~ ·S
~ = 0. Also gibt es keine Spin-Bahn1. Im Singulettzustand (|S|
~ +S
~ = L,
~
Kopplung, und der Gesamtdrehimpuls ergibt sich nur aus dem Bahndrehimpuls (J~ = L
2
2
~ = l · (l + 1) · ~ ).
wobei L
~ = 1, also ergeben sich mit L
~ = ~l1 + ~l2 drei Möglichkeiten:
2. Im Triplettzustand ist |S|
~ +1
J~1 = L
~ +0
J~2 = L
~ −1
J~3 = L
Der tiefste Zustand ist 23 P2,1,0 (in der Schreibweise n(2S+1) LJ1 ,J2 ,J3 ). Wir führen eine Schreibweise
für die Zweielektronensysteme ein und suchen mögliche Zustände mithilfe des Pauli-Prinzips:
• Der tiefste Zustand ist 1s2 mit der Konfiguration 11 S0 .
1
e−
1 : n1 = 1, l1 = 0, ml1 = 0, ms1 = 2
1
e−
2 : n2 = 1, l2 = 0, ml2 = 0, ms2 = − 2
»
º
−
Wir folgern, dass e−
1 und e2 anhand des Spins Pauli-unterscheidbar sind.
~ = 1 gefordert wird, also müssten
• Der Triplettzustand 1s2 , 13 S1 ist nicht möglich, da |S|
beide Elektronen den 1-Spin haben, wodurch sie nicht mehr unterscheidbar wären.
~ = 0) und das
• Die nächsten möglichen Zustände sind das Singulett 1s2s, 21 S0 (mit |S|
3
~ = 1). Hier sind die Elektronen aufgrund der unterschiedlichen
Triplett 1s2s, 2 S1 (mit |S|
Hauptquantenzahlen Pauli-unterscheidbar. Damit haben wir den niedrigsten Zustand für
ein Triplett.
• Höhere Zustände sind die P - und D-Zustände wie 1s2p, 23 P2,1,0 und 1s3d, 31 D3,2,1 . Diese
Zustände sind allerdings sehr kurzlebig.
Zur Abbildung 1.36:
• Dipolübergänge folgen den Übergangsregeln ∆L = ±1, ∆J = 0, ±1 und ∆S = 0.
• Deswegen gibt es kein Intersystem-Crossing, dass heißt es finden keine Übergänge zwischen
Singulett- und Triplett-Zuständen.
6.5 Aufbauprinzip. Periodensystem der Atome
Seite 51
• Aufgrund der Heisenbergschen Austauschenergie K liegt das Niveau 23 S1 tiefer als 21 S0 .
• Die Feinstruktur der Triplett-Zustände hat zwei Ursachen:
1. Spin-Bahn-Kopplung innerhalb der Elektronen: ~l1 · ~s1 und ~l2 · ~s2
2. Spin-Bahn-Kopplung zwischen den Elektronen (starke Wechselwirkung): ~l1 ·~s2 und ~l2 ·~s1
Für He existiert dadurch eine unübliche Feinstrukturaufspaltung, die gegenüber dem H-Atom
eine invertierte Abfolge besitzt. (Siehe dazu Abbildung 1.37.). Diese Invertierung folgt aus der
starken Wechselwirkung zwischen den Elektronen.
• Aufgrund der geringen Elektronenzahl ist die Abschirmung des Kernpotentials nicht sehr effektiv.
Die resultierende Hyperfeinstrukturaufspaltung soll hier aber nicht behandelt werden.
6.5 Aufbauprinzip. Periodensystem der Atome
Als Basis für den Aufbau nehmen wir natürlich das Pauli-Prinzip. Die vier Quantenzahlen n, l, ml
und ms müssen unterscheidbar sein. Man beachte, dass die Konfiguration nur für die letzte Schale
vermerkt ist, da die aufgefüllten Schalen inert und damit ohne Einfluss auf die Systemenergie sind.
Element
Wasserstoff (H)
Helium (He)
Lithium (Li)
Beryllium (Be)
Bor (B)
Kohlenstoff (C)
Stickstoff (N)
Sauerstoff (O)
Fluor (F)
Neon (Ne)
e− -Zahl
1
2
3
4
5
6
7
8
9
10
Grundzustand
1s
12 S1/2
1s2
11 S0
1s2 2s
22 S1/2
2
2
1s 2s
21 S0
1s2 2s2 2p
22 P1/2
1s2 2s2 2p2 23 P0
1s2 2s2 2p3 24 S3/2
1s2 2s2 2p4 23 P2
1s2 2s2 2p5 22 P3/2
1s2 2s2 2p6 21 S0
Diese Tabelle erklärt sich mit den Hundschen Regeln.
Im Grundzustamd eines Atoms hat der Gesamtspin den größtmöglichen mit dem Pauli-Prinzip vereinbaren Wert.
1. Hundsche Regel
Wir können die Schalen nach folgenden Regeln auffüllen:
• Für l = 0 kann man 2e− auffüllen.
• Für l = 1 kann man 6e− auffüllen.
• Für l = 2 kann man 10e− auffüllen.
• Für l = 3 kann man 14e− auffüllen.
• Allgemein kann man für ein festes l maximal 2 · (2l + 1) Elektronen.
6.5 Aufbauprinzip. Periodensystem der Atome
Seite 52
Die Schalenkapazität ergibt sich aus der Summe der Kapazitäten für alle möglichen l. Wir führen die
folgenden Bezeichnungen ein:
n 1 2 3 4 5 ···
Code K L M N O · · ·
e− Zahl 2 8 18 32 50 · · ·
Bis jetzt haben wir nur die K- und die L-Schale aufgefüllt:
• Die K-Schale wird aufgefüllt für H, He.
• Die L-Schale wird während des Durchlaufs von Li, Be, B, C, N, O, F, Ne gefüllt.
• M-Schalenelemente sind zum Beispiele alle Elemente von Na (1s2 2s2 2p6 3s) bis Ar (1s2 2s2 2p6 3s2 3p6 ).
• Achtung: Die Weiterführung erfolgt nicht für die 3d-Elektronen. Stattdessen füllen Z = 19 (K)
und Z = 20 (Ca) zunächst die 4s-Elektronen auf, erst darauf folgen die 3d-Elektronen. Analog
zu 4s ↔ 3d gi
Z = 19: K
(1s2 2s2 2p6 3s2 3p6 4s)
Z = 20: Ca (1s2 2s2 2p6 3s2 3p6 4s2 )
Z = 21: Sc (1s2 2s2 2p6 3s2 3p6 4s2 3d1 )
Z = 22: T
(1s2 2s2 2p6 3s2 3p6 4s2 3d2 )
Z = 23: V
(1s2 2s2 2p6 3s2 3p6 4s2 3d3 )
Z = 24: Cr (1s2 2s2 2p6 3s2 3p6 4s1 3d5 )
Z = 25: Mn (1s2 2s2 2p6 3s2 3p6 4s2 3d5 )
• Achtung: Chrom hat eine Unregelmäßigkeit. Ein 4s-Elektron geht vorübergehend in die 3d-Schale
über, um dort alle »-Zustände aufzufüllen. Dies tritt zum Beispiel auch bei Z = 29 mit der
Konfiguration 1s2 2s2 2p6 3s2 3p6 4s1 3d10 ein, ebenso bei höheren Niveaus.
Aufgrund der Unregelmäßigkeiten in der Schalenauffüllreihenfolge für höhere Z-Zahlen hat man einige
neue Materialklassen von Übgergangselementen eingeführt:
1. Die Elemente Z = 21 bis Z = 30 bilden die Eisengruppe.
2. Die Elemente Z = 39 bis Z = 48 bilden die Palladiumgruppe.
3. Die Elemente Z = 71 bis Z = 80 bilden die Platingruppe.
Weitere Unregelmäßigkeiten sind durch die folgenden Gruppen erfasst:
• Die Elemente Z = 57 bis Z = 70 bilden die seltenen Erdmetalle, die Lanthanoide.
• Die Elemente Z ≥ 89 bilden die Actinoide.
Das sich ergebende Periodensystem, wie es heute vorliegt, wurde 1869 parallel und voneinander unabhängig von Mendelejew und Meyer entwickelt.
6.5.1 Ionisationsenergien der Atome
Element
H
He
Li
Ionisationsenergie Ei /[eV]
13,6
24,6
5,39
Begründung
ein Elektron im 2s-Zustand mit größerem Kernabstand
somit kleinere effektive Abschirmung
6.6 Spektrum der Alkali-Atome
Seite 53
Die Abschirmung ist minimal bei Edelgasen und optimal bei Alkaliatomen mit ZEdelgas + 1, wie zum
Beispiel bei Li, Na und K. Diese sogenannten sind besonders reaktiv. Wie man sieht, kann man mithilfe
des Periodensystems direkt die folgenden Eigenschafen abschätzen:
• chemische Reaktivität
• Bindungsenergie
Zum Beispiel gilt für die folgenden Elementgruppen:
• Edelgase sind relativ inert.
• Alkaliatome sind sehr reaktiv.
• Halogene wie F, Cl sind sehr aktive Elemente.
6.6 Spektrum der Alkali-Atome
Zu dieser Gruppe gehören die Elemente Li, Na, K, Rb, Cs. Aus dem Termschema des Li-Atoms in
Abbildung 1.39 entnehmen wir allgemein:
• Die Terme sind nach S, P, D, . . . geordnet.
• Die Energiezustände sind relativ zum tiefstliegenden Niveau 2s der Atome referenziert.
• Man kann diese Spektren der Atome mit H vergleichen.
• Durch verschiedene Strichstärken markiert man die Intensität der Übergänge.
• Die Beschriftungen entlang der Übergänge beziffern die Wellenlänge in nm.
• Die Übergänge genügen den Dipolauswahlregeln ∆j, ∆l = −1, 0, 1.
Zum Beispiel die Übergänge: 2 S1/2 → 2 P1/2,3/2 als Dublett und 2 D3/2,5/2 → 2 P1/2,3/2 als Triplett.
Alkaliatome sind, ähnlich wie H-Atome, Einelektronensysteme. Zur Beschreibung eines Niveaus benutzen wir den Termwert:
R
E
T =
=− ∗ 2
h·c
(n )
Hierbei ist E die Energie des Zustandes, R die Rydberg-Konstante (in der Grobstruktur) und:
n∗ = n − α(l) +
β(l)
n2
Wir führen n∗ mit den Korrekturfaktoren α(l) und β(l) ein und erhalten eine neue „effektive Hauptquantenzahl“. Die Ursache der Korrekturen ist das Eindringen von äußeren Elektronen in den Atomrumpf, auf sogenannten Tauchbahnen (siehe Abbildung 1.42). Die Größe und Struktur dieser Korrektur wurde rein empirisch ermittelt. Für das Na-Atom findet man zum Beispiel, dass die 3s- und
3p-Elektronen aufgrund der starken Wechselwirkung mit dem Kern Tauchbahn aufweisen. Hingegen
dringen 3d-Elektronen nicht in den Atomrumpf ein.
Man kann diese Korrektur auch als Quantendefekt formulieren:
∆(n, l) = n − n∗ = α(l) −
β(l)
n2
Relavant ist diese Korrektur für die Zustände S (∆(n, 1) ≈ 1,3) und P (∆(n, 2) ≈ 0,8), für höhere
Zustände werden die Quantendefekte sehr klein (zum Beispiel ∆(n, 3) ≈ 0,01).
6.8 Multiplett-Spektrum der Mehrelektronensystem
Seite 54
Feinstruktureinflüsse ergeben sich analog zum H-Atom für l 6= 0, also j = l±1/2. Wiederum ist ∆Efs ∼
Z 4 /n3 weitaus stärker als die relativistische Korrektur. Wir sehen, dass schwere Alkali-Atome zu einer
großen Aufspaltung führen (für H ist ∆E = 0,42 · 10−4 eV, für Cs hingegen ist ∆E = 6,87 · 10−1 eV
um vier Größenordnungen größer).
Nun sind noch die Hyperfeinstruktureinflüsse zu betrachten. Alle Alkali-Atome haben eine ausgeprägte
Hyperfeinstrukturaufspaltung. Dazu gibt es drei Möglichkeiten, die wir anhand von drei typischen
Beispielen sehen werden.
• scharfer Übergang (die Übergänge haben eine Frequenzunschärfe, sind aber voneinander klar zu
trennen; zum Beispiel bei Na23 mit j = 3/2)
• breiter Übergang (alle scharfen Übergänge sind wegen ähnlicher Energiewerte überlagert; etwa
bei Li6 mit j = 1)
• intermediärer Übergang (einige Übergänge sind scharf messbar, andere sind überlagert; z.B. Li7 )
6.7 Spektrum der Erdalkali-Atome und Zweielektronen-Systeme
Zu der Gruppe der Zweielektronensysteme gehören Zn, Cd, Hg. Erdalkali-Atome sind definiert als
Alkali-Atome zu denen ein Elektron hinzukommt. Die Zustände werden bezogen auf das He-Atom.
Be(. . . 2s2 , 21 S0 )
Mg(. . . 3s2 , 31 S0 )
Ca(. . . 4s2 , 41 S0 )
Sr(. . . 5s2 , 51 S0 )
Ba(. . . 6s2 , 61 S0 )
Ra(. . . 7s2 , 71 S0 )
Wir haben also 2e− -Systeme, welche die optischen Eigenschaften bestimmen. Wiederum gibt es Singulett, Dublett- und Triplettübergänge gemäß den bekannten Dipolübergangsregeln. Ebenfalls gibt es einen
Quantendefekt aufgrund von Tauchbahnen, die für kleine l einen prominenten Einfluss auf die Elektronenenergie haben.
Ähnliche Eigenschaften wie die Erdalkaliatome sind die Zweielektronensystem Zn, Cd und Hg. Hier
gibt es noch zehn weitere Elektronen in einer nicht aufgefüllten, tieferen Schale; die Übergänge werden aber vorrangig durch die äußeren ns2 -Elektronen bestimmt. Neu ist, dass es zusätzlich einige
Übergänge zwischen bestimmten Singulett- und Triplettzuständen gibt, obwohl dies scheinbar durch
die Auswahlregeln eigentlich verboten ist. Die Ursache für diese Interkombinationsübergänge liegt
darin, dass es neben der LS-Kopplung auch eine intermediäre Kopplung der Zustände gibt, weshalb
die Niveaus (und damit die Übergangsmatrixelemente) nicht mehr scharf begrenzt sind.
6.8 Multiplett-Spektrum der Mehrelektronensystem
Nach den ns-Schalen wie in 6.6 und der ns2 -Schalen aus 6.7 kommen nun die np- und die nd-Schalen
hinzu. Wichtige Beispiele für np-Übergänge sind:
• Al(1s2 2s2 2p6 3s2 3p) – Man unterteilt die Übergänge in einfache Terme (Dubletts 3n2 nl) und
komplexe Terme (Dubletts und Quartetts 3s3p nl). Eine reine Darstellung von Singulett- und
Triplettübergängen ist nicht mehr möglich.
6.10 Energiestruktur der inneren Elektronenschalen
Seite 55
• O(ns2 np4 , 3 P2 ) – Markant ist der Übergang zwischen 1 S und 1 D mit ∆l = ±2. Bis jetzt hatten
wir nur Dipolübergänge mit ∆l = ±1, dies ist nun aber ein Quadrupolübergang. Dieser Übergang
ist als Aurora-Linie bekannt und die Ursache der grünen Variante des Nordlichtes.
• Halogene (ns2 np5 ) – Das wichtigste Beispiel ist F. Auch hier haben wir markante Dipol- und
Quadrupolübergänge (entsprechend Dublett- und Quartettzuständen).
• Edelgase (ns2 np6 , n1 S0 ) – Hier ist die p-Schale abgeschlossen, somist verschwinden die Gesamt~ = |S|
~ = |J|
~ = 0. Entfernt man ein Elektron aus der Schale (Ionisation), so
drehimpulse |L|
ergibt sich ein Loch e+ . Das entstehende Ion (ns2 np5 ) hat die Konfiguration 2 P1/2,3/2 .
Man beobachtet in diesem Ion einen neuen Effekt: Die Elektronen koppeln an das Loch, und es
~ = ~j + ~l. Wir bezeichnen diese Zustände mit (P1/2 )l[K]J oder
entsteht ein Gesamtdrehimpuls K
(P3/2 )l[K]J , wobei J der Gesamtdrehimpuls ist. Diese neue Art von LS-Kopplung führt unter
anderem dazu, dass bei n = 3 eine Verdoppelung gibt.
Die Behandlung der nd-Übergänge ist völlig analog, nur ungleich komplexer.
6.9 Energiestruktur von Ionen
Positiv geladene Ionen An+
Wir haben die isoelektrische Reihe, also Atome mit gleicher Anzahl von Elektronen.
• H-artige Ionen: H, He+ , Li2+ , Be3+ , ..., U91+ , ...
• He-artige Ionen: Li+ , Be2+ , B3+ , ..., Lw101+ , ...
• Cu-artige Ionen: Zn+ , Ga2+ , ..., Xe25+ , ...
Zwischen den Elektronen gibt es die Coulomb-Wechselwirkung, die mit Z 2 zunimmt. Hinzu kommen:
• bei den H-artigen Atomen: für l 6= 0 eine Dublett-Aufspaltung ∼ Z 4
• bei He-artigen Atomen: für n ≥ 2 eine Coulombenergie ∼ (Z − δ)2 (hierbei beschreibt δ die von
l abhängige Abschirmung der Kernladung)
Negative Ionen An−
Im Allgemeinen werden diese Ionen analog zu den positiv geladenen Ionen betrachtet, können aber
meistens nur ein Elektron aufnehmen. Die Bindungsenergie dieses Elektrons wird als Elektronenaffinität (EA) bezeichnet. Für ein beliebiges elektrisch neutrales Atom A im Grundzustand ergibt sich
EA durch:
EEA (A) = Etot (A) − Etot (A− )
Hierdurch erhält man eine Klassifikation, welche Atome Elektronen aufnehmen können: Für Energiedifferenzen EEA (A) > 0 ist A− stabil. (Benutzt man Tabellenwerte zur Berechnung, muss man auf
das Vorzeichen aufpassen, denn die Gesamtenergie ist negativ.) Besonders hoch sind die Elektronenaffinitäten für Halogene und die Edelmetalle Cu, Ag und Au. Negative Elektronenaffinitäten treten bei
abgeschlossenen Schalen, also bei Erdalkaliatomen und Edelgasen, auf; hier sind die entsprechenden
A− -Ionen instabil.
6.10 Energiestruktur der inneren Elektronenschalen
Seite 56
6.10 Energiestruktur der inneren Elektronenschalen
Konrad Röntgen fand 1896, dass Atome in der Lage sind, Röntgenstrahlen im Bereich zwischen 10 pm
und 10 nm zu emittieren. Dabei wird das Atom durch ein einfallendes Elektron zunächst ionisiert, wobei
aus einer der inneren Schalen (zum Beispiel der K-Schale) ein Elektron herausgeschlagen wird. Dann
fallen Elektronen in den oberen Niveaus in das entstehende Loch. Wir haben also zum Beispiel einen
Übergang von A+ (K) zu A+ (L) unter Abgabe von Strahlung ∆EKL = h · νKL , dann einen Übergang
von A+ (L) zu A+ (M ) unter Strahlungsabgabe, und so weiter. Diese Abfolge nennt man Kaskade.
Das entstehende Spektrum besteht aus der Bremsstrahlung des Elektrons im Atomverband, jedoch
überlagert von einigen scharfen Spitzen, die durch die Übergänge in der Kaskade verursacht wird.
Ähnlich zum H-Atom gibt es eine Grobstruktur:
En = −R · hc ·
(Z − δn )2
n2
Hierbei sind R die Rydberg-Konstante und δn die effektive Nukleonenabschrimung. Die Feinstruktur
kennen wir auch noch:
·
¸
hc · R · α2 · (Z − δn )4
1
3
Ej,l = −
·
−
n3
j + 1/2 4n
7.1 Zeeman-Effekt
Seite 57
7 Atome in äußeren Feldern
Wir unterscheiden:
• statische Felder: Magnetfelder (Zeeman-Effekt) und elektrische Felder (Stark-Effekt)
• dynamische Felder: Lichtwellen (v.a. Laser mit f ≈ 1015 Hz, Berechnung mit Quantenelektrodynamik)
Äußere Felder führen zu einer Änderung der energetischen Zustände im Atom:
• Aufspaltung der Energieniveaus
• Verschiebung der Energieniveaus
• Überlagrund von Zuständen (Hybridisierung)
7.1 Zeeman-Effekt
Dieser Effekt wurde 1896 von dem Niederländer Pieter Zeeman entdeckt. Er schaute sich das Spektrum
eines Atoms an: Ohne ein äußeres Feld und er erhielt ein einzelnen scharfen Peak. Beim Anlegen eines
Magnetfeldes werden daraus sehr viele Peaks, die von einer Glockenkurve eingehüllt sind. Die Erklärung
lieferte Lorentz mit einer klassischen Theorie. Damit kann man allerdings nur den normalen ZeemanEffekt erklären. Für den anormalen Effekt benötigt man die Fein- und Hyperfeinstruktur.
7.1.1 Normaler Zeeman-Effekt. Lorentz-Tripletts
Wir betrachten wieder ein Elektron, das den Atomkern in der xy-Ebene mit dem Abstandsvektor ~r
~ k ~ez zugeschaltet.
und der Geschwindigkeit ~v umkreist. Nun wird ein externes Magnetfeld B
Auch ohne Magnetfeld haben wir eine Zentripetalkraft: F0 = |F~0 | = mω02 ·r. Hinzu kommt nun die Lorentzkraft Fl = eω1 · r · B. Hierbei unterscheiden wir die Winkelgeschwindigkeit ω0 ohne Magnetfeld und
die neue Winkelgeschwindigkeit ω1 . Die beiden Kräfte fügen sich zu einem neuen Kräftegleichgewicht
zusammen:
vorher:
F0 = mω02 · r
jetzt:
F0 + Fl = mω12 · r
2
mω0 · r + eω1 · rB = mω·12 · r
¸
q¡ ¢
eB
eB 2
1
2
+ 4ω0
ω1 = 2 · m ±
m
Uns interessiert der Fall eB/m ¿ 2ω0 . Dann ist:
ω1 = ω0 ±
eB
2m
7.1 Zeeman-Effekt
Seite 58
Der Zeeman-Effekt führt also auf eine Frequenzmodulation. Im Allgemeinen müssen wir aber zwei
Beobachtungsrichtungen unterscheiden, einmal in z-Richtung (entlang des Magnetfeldes) und einmal
in der Ebene der Elektronenbahn (x − y-Ebene).
1. longitudinaler Zeeman-Effekt: Beobachtungsrichtung entlang der z-Achse; zwei Spektrallinien
ν10 =
ω0
eB
+
2π 4π · m
und
ν20 =
ω0
eB
−
2π 4π · m
Das entstehende Licht bezeichnen wir als σ-polarisiert. Das Licht mit ν10 ist links zirkular
polarisiert, das Licht mit ν20 ist rechts zirkular polarisiert.
2. transversaler Zeeman-Effekt: Beobachtungsrichtung senkrecht zur z-Achse; drei Spektrallinien
ν0 =
ω0
2π
und
ν100 =
ω0
eB
+
2π 4π · m
und
ν200 =
ω0
eB
−
2π 4π · m
Das entstehende π-polarisierte Licht ist entweder parallel zu z (ν0 ) oder senkrecht zu z und der
Beobachtungsrichtung (ν100 , ν200 ) polarisiert.
Wir wollen diese Effekte jetzt quantenmechanisch erklären. Dabei vernachlässigen wir den Elektronen~ ≈ 0. Somit müssen wir nur den Bahndrehimpuls L
~ berücksichtigen. Nach Bohr muss dieses
spin, also |S|
~ verknüpft sein. Durch ein äußeres magnetisches
mit einem magnetischen Moment µ
~ l = −ml · µ
~ B = L/~
Feld kommt es demnach zu einer Änderung der potentiellen Energie und einer neuen Gesamtenergie:
~
∆EB = −~
µl · B
⇒
E = Enl + ∆EB
Aus den Auswahlregeln ∆ml = −1, 0, 1 folgt:
• σ-polarisiertes Licht für ∆ml = ±1, also ∆ω = ±eB/2m
• π-polarisiertes Licht für ∆ml = 0 und ∆ω = 0
Wir schätzen die Stärke des Zeeman-Effektes in der Grobstruktur ab:
µ ¶
1
µB · B
1
∆ν = ∆
=
= 4,665 · 10−3 · B ·
λ
h·c
m · Tesla
Zum Beispiel für B = 2 T ist ∆ν ≈ 1 cm−1 und somit ∆λ ≈ 0,025 nm. Dieser Einfluss ist vernachlässigbar, relevant wird der Zeeman-Effekt erst in der Feinstruktur.
7.1.2 Anomaler Zeeman-Effekt
Wir unterscheiden die folgenden Bereiche:
1. ∆EB ¿ ∆ELS (Russel-Saunders-Bereich)
2. ∆EB ≈ ∆ELS (nichtlineare Lösung, im Folgenden nicht berücksichtigt)
3. ∆EB À ∆ELS (Paschen-Back-Bereich)
7.1 Zeeman-Effekt
Seite 59
Zum Russel-Saunders-Bereich
Wir nehmen an, dass ∆Ehf s = 0 ist. Damit setzt sich der Hamiltonoperator aus dem normalen kinetischen Term, der Feinstruktur-Korrektur und der Zeeman-Korrektur zusammen:
H = H 0 + H LS + H B
Der neue Anteil ist:
~
HB = −~
µj · B
~ = P ~si und dem GesamtbahndreDabei ist J~ der Gesamtdrehimpuls, der sich aus dem Gesamtspin S
i
~ = P ~li zusammensetzt. Das magnetische Moment hat die Form:
himpuls L
i
!
Ã
X
X
µ
~B ~
µ
~
B
~li + gs ·
~ =−
µ
~j = −
~s + µ
~l
· (L + 2S)
· gl ·
~si = µ
~
~
i
i
Der Betrag ist dann:
¸
J 2 + S 2 − L2
|~
µj | = µj = −µB · J · 1 +
2J 2
|
{z
}
·
=gj
gj ist der Landé-Faktor für die LS-Kopplung.
µj = −µB · gj · J
und
∆EB = mj · gj · µB · B
z-Aufspaltung für LS-Kopplung
Wir betrachten als Beispiel die Na-D-Linien: Im Grundzustand 32 S1/2 ist ms = ±1/2, somit spaltet
sich dieser Zustand in zwei Energieniveaus (also ein Dublett) auf. Dabei ist:
1
∆EB = ± · 2 · µB · B = ±µB · B
2
Im nächsthöheren Zustand 32 P1/2 ist j = 1/2, s = 1/2 und l = 1, somit ist:
gj = 1 +
j(j + 1) + s(s + 1) − l(l + 1)
2
=
2 · j(j + 1)
3
Der Zustand spaltet sich wiederum in zwei
nen:
1
∆EB = ±
2
Energieniveaus auf. Damit kann man die Energie errech·
2
1
· µB · B = ± · µB · B
3
3
Betrachten wir den nächsthöheren Zustand 32 P3/2 . Hier ist j = 3/2, mj = ±1/2, ±3/2 und damit
gj = 4/3. Dieser Zustand spaltet sich in vier Energieniveaus auf, deren Energie ist:
∆Emj =±3/2 = ±2 · µB · B
und
∆Emj =±1/2 = ± 23 · µB · B
In wie viele Übergänge spalten sich die Na-D-Linien nun auf? Mithilfe der Auswahlregeln findet man:
• Die D1 -Linie zwischen 32 S1/2 und 32 P1/2 teilt sich in 4 Übergänge auf.
• Die D2 -Linie zwischen 32 S1/2 und 32 P3/2 teilt sich in 6 Übergänge auf.
Für die Zustände 20 mit ∆EB ≈ ∆ELS erfordert mehr quantenmechanischen Aufwand, da nichtlineare
Abhängigkeiten vorkommen.
7.1 Zeeman-Effekt
Seite 60
Zum Paschen-Back-Effekt
~ und S
~ koppeln separat zum B-Feld.
~
Hier haben wir eine Analogie zur JJ-Kopplung: L
Die magnetischen
Momente addieren sich:
µj = −
µB
µB
· (gl · ml + gs · ms ) = −
· (ml + 2 · ms )
~
~
Damit ist dann die Energiedifferenz:
∆EB = −µz · B = µB · B · (ml + 2ms )
Durch die Auswahlregeln ∆ms = 0 und ∆ml = −1, 0, 1 kann man wie oben die Aufspaltung von
Übergängen beschreiben.
Zeeman-Effekt mit Hyperfeinstrukturaufspaltung
Wir haben hier eine IJ-Kopplung und können wieder drei Bereiche unterscheiden:
hfs ¿ ∆E
• 10 : ∆EB
hfs – lineare Abhängigkeit
hfs ≈ ∆E
• 20 : ∆EB
hfs – nichtlineare Abhängigkeit (intermediärer Bereich)
hfs À ∆E
• 30 : ∆EB
hfs – lineare Abhängigkeit
Hierbei ist ∆Ehfs die Energieänderung der Hyperfeinstruktur ohne äußeres Magnetfeld.
~
Zum ersten Fall: Hier dominiert die IJ-Kopplung, man erhält einen Gesamtdrehimpuls F~ = I~ + J,
~
welcher um die Quantisierungsachse (hier in Richtung von B k ~ez ) präzediert. Wir erhalten ein magnetisches Moment:
~ F~ ) − µi · cos(I,
~ F~ )
µf = µj · cos(J,
Damit ergibt sich die Hyperfeinstrukturaufspaltung:
hfs = m · g · µ · B
∆EB
B
f
f
Der Landé-Faktor ist gegeben durch:
gf = gj ·
J F 2 + J2 − I2
me
I F 2 + I2 − J2
·
−
· gi · ·
F
2F J
mp
F
2F I
Der hintere Summand ist aufgrund des Verhältnisses me /mp ≈ 10−3 , welches bei größeren Kernen nur
noch kleiner wird, vernachlässigbar.
gf = gj ·
J F 2 + J2 − I2
·
F
2F J
Damit erhält man für J 6= 0 eine Aufspaltung in (2J + 1) · (2F + 1) Terme. Wir wollen den Einfluss
dieser Aufspaltung abschätzen. Zunächst ist:
∆Ehfs ≈ µi · BKern (~r = 0)
|
{z
}
≈100 T
und
hfs
∆EB
≈ µB · B
7.1 Zeeman-Effekt
Seite 61
Aus beiden Termen erkennen wir:
hfs
∆EB
.
µi
· ∆Ehfs
µB
⇒
B . 0, 1 T
Nun betrachten wir den dritten Fall, der wieder als Paschen-Back-Effekt (der Hyperfeinstruktur)
bezeichnet wird. Hier präzedieren J~ und I~ unabhängig voneinander und in entgegengesetzter Richtung
um die Quantisierungsachse. Die gesamte Aufspaltung erhalten wir aus der Summe der Effekte:
hfs
J
I
∆EB
= ∆EB
+ ∆EB
Die einzelnen Komponenten lauten wie folgt:
J
~ B)
~ · µB · B = mj · gj · µB · B
∆EB
= gj · cos(J,
m
I
~ B)
~ · µB · B
∆EB
= − mpe · gi · cos(I,
I kommt aus der umgekehrten Präzessionsrichtung. Auch hier ist (aufgrund des
Das Minus in ∆EB
I sehr gering.
enthaltenen Massenverhältnisses) der Anteil von ∆EB
~ J)
~ = A · mj mi
∆Ehfs = A · JI · cos(I,
Die Gesamtenergie des Paschen-Back-Effekts in der Hyperfeinstrukturaufspaltung:
J + ∆E I + ∆E
∆EPB = ∆EB
hfs ≈ mj · gj · µB · B + A · mj mi
B
hfs À ∆E
~
Es gilt natürlich die Abschätzung ∆EB
hfs für Magnetfelder |B| & 0, 1 T. Zudem gilt die
Multiplizität, also (2F + 1) · (2J + 1) und es entsteht eine Umverteilung.
7.1.3 Quadratischer Zeeman-Effekt: Diamagnetismus und
Landaubereich
Es geht um den nichtlinearen Bereich in der Fein- und Hyperfeinstruktur.
1. ∆EB ≈ ∆ELS
~
2. Präzession des Elektrons im B-Feld
macht eine Rückkopplung über die Induktion, damit Beeinflussung des magnetischen Moments µ
~l
Landau fand eine diamagnetische Suszeptibilität. Diese soll mit dem Hamilton-Operator hergeleitet
werden.
0
00
H = H0 + H + H
~ beschreibt den linearen Zeeman-Effekt. Der zweite Term ist nichtlinear und
Der Term H 0 = −~
µ·B
beschreibt den sogenannten Diamagnetismus. Der Lösungsansatz ist, vom Impuls ~p überzugehen zu
~ mit dem Vektorpotential:
~p + e/c · A
³
´
~=1· B
~ ×~r
A
2
Mit dem neuen Impuls ergibt sich der folgende Hamiltonoperator:
H=
p2
00
∼ B 2 · r2 ∼ H
2m
7.2 Stark-Effekt
Seite 62
Explizit ist:
00
H =
e2 · B 2 2
·~r · sin2 ϕ
8m
~ r). Aus geometrischen Überlegungen folgt r2 · sin2 ϕ = x2 + y 2 . Den Vorfaktor
Hierbei ist ϕ = ^(B,~
kann man mit der Zyklotronfrequenz ωc = eB/2m vergleichen. Damit hat man:
00
H =
1
· mωc2 · (x2 + y 2 )
2
Das entspricht einem harmonischen Oszillator in der xy-Ebene. Somit ist die Energie quantisiert, und
die Gesamtenergie ergibt sich wie folgt:
¶
µ
~2 · kz2
1
· ~ωc +
E = n+
2
2m
Der erste Term entspricht der Energie in der xy−Ebene und der zweiter Term ist die Energie in
z-Richtung. Die Bewegung in der xy-Ebene folgt also dem Landau-Niveau. Die Lösung über die
Potentiale erfolgt jetzt über eine Kombination des atomaren Potentialtopfes und der parabolischen
Abhängigkeit durch die Landau-Quantisierung. Dadurch wird das Potential nichtlinear.
7.1.4 Zusammenfassung
Mit steigender Feldstärke ergeben sich die folgenden Bereiche:
00 | ¿ |H |
1. linearer Zeeman-Effekt (Coulomb-Limit, Paramagnetismus): |HB
0
⇒
~
∆E ∼ B
2. Paschen-Back-Bereich
3. l-mischender Bereich
4. n-mischender Bereich
00 | ≈ |H |
5. Quasi-Landau-Breich: |HB
0
00 | À |H |
6. Landau-Bereich (Diamagnetismus): |HB
0
⇒
~2
∆E ∼ B
7.2 Stark-Effekt
Der Stark-Effekt beschreibt die Aufspaltung und Verscheibung von Spektrallinien und atomaren
Zuständen in einem äußeren elektrischen Feld. 1913 entdeckten Stark und Lo Surdo den Effekt
anhand der Balmerlinien im H-Atom. Es waren Verschiebungen in den Übergängen zu beobachten.
Wiederum gibt es lineare und quadratische Ausprägungen des Stark-Effekts:
1. linearer Stark-Effekt: im Falle ∆EStark À ∆Efs (dominant für H-artige Atome)
2. quadratischer Stark-Effekt: im Falle ∆EStark ¿ ∆Efs oder bei S-Zuständen mit ∆Efs = 0
(dominant für Mehrelektronensysteme)
7.2 Stark-Effekt
Seite 63
7.2.1 Erste Ordnung der Störungsrechnung
~ da E bereits für
Das Atom sei einem elektrischen Feld F~ [V/m] ausgesetzt. (Wir schreiben nicht E,
die Energie vergeben ist.) Das Feld ist in der Quantisierungsrichtung ausgerichtet (F~ k ~ez ). Es ergibt
F
sich im Hamiltonoperator ein Störungsterm H (als zusätzliche potentielle Energie) mit
H F = eF · z
Wir wollen im Folgenden den Elektronenspin vernachlässigen. Wir erhalten Lösungen mit der Hamiltonwellenfunktion, insbesondere den Zustand:
ψn,l,m (~r)
⇒
ψ1,0,0
Für diesen Zustand ergibt sich die Energieaufspaltung in der ersten Ordnung der Störungsrechnung:
Z
(1)
∆E100 = eF · hψ100 | z |ψ100 i = eF · |ψ100 |2 · z dΩ
Der hintere Term ist eine Analogie zu Dipolmatrixübergangselementen (hier jedoch für einen „Übergang“ von einem zum selben Term). Auf jeden Fall ersehen wir hieraus, dass das Integral lösbar ist. Für
ein Matrixelement h ψnlm | zψnl0 m i, welches einen Übergang darstellt, gilt ∆l = ±1. Hier ist ∆l = 0. Es
ergibt also in der ersten Ordnung kein Beitrag.
7.2.2 Zweite Ordnung der Störungsrechnung
Wir nehmen eine quadratische Abhängigkeit in F~ an. Nach einiger Rechenarbeit kommt man für 1sElektronen auf:
X hψnlm | z |ψ100 i2
(2)
∆E100 = −e2 F 2 ·
En − E1
n6=1
l,m
In den Summanden stehen Matrixübergangselemente. Also spielen nur solche Quantenzahlen n, l, m
eine Rolle, die den Übergangsregeln gehorchen.
(2)
∆E100 = −8πε0 ·
a30
Z4
· F2
Stark-Effekt im H-Atom
Diese Formel ist plausibel, denn dieser Energiebeitrag verschwindet nur für |F~ | =
6 0. Um einen Eindruck von der Stärke des Stark-Effektes zu bekommen, nehmen wir zum Beispiel ein Feld von
F = 105 V/cm = 10 mV/nm an:
|∆E (2) | = 25 · 10−8 eV
⇒
∆k = 2 · 10−4 cm−1
Dies ist ein verschwindend geringer Einfluss. Wir haben also ein induziertes Dipolmoment:
~pind =
(2)
X
∂ (∆E100
Energie
=
= −2e2 F~ ·
· · · = −α · F~
el. Feld
∂ F~
Hierbei ist α die elektrische Dipolpolarisierbarkeit mit
α = 2e2 ·
Allgemein gilt nun:
X
· · · = 16πε0 ·
a30
1 C · nm2
−23
=
7,42
·
10
·
Z4
Z4
V
7.2 Stark-Effekt
Seite 64
(2)
∆E100 = − α2 · F~ 2
Die elektrische Dipolpolarisierbarkeit ist ein typischer Tabellenwert für verschiedene Atome.
7.2.3 Starkeffekt für Zustände n > 1
Hier kommen wir zu einem linearen Stark-Effekt. Zunächst betrachten wir den Fall n = 2. Damit
haben folgende mögliche Zustände (rechts in der Schreibweise |lml i):
|2si→|00i
|2pi→|11i , |10i , |1, −1i
Wir betrachten wiederum die Matrixübergangselemente:
hψnlm | z |ψnl0 m0 i =
6 0
⇒
∆l = ±1
und
∆ml = 0
In den Zuständen |11i und |1, −1i sind keine Übergänge möglich, folglich kann man hier keine StarkEffekt-Aufspaltung erwarten. Nun die Zustände |00i und |10i erfahren eine lineare Verschiebung ∆E (1) .
Die erste Ordnung der Störungsrechnung basiert auf dem Störungsoperator:
H
F
= eF · z
Damit ergibt sich die folgende Schrödingergleichung:
¡
¢
H |ψi = H 0 + eF · z · |ψi = E (1) · |ψi
Wir machen einen Lösungsansatz:
|ψi = a1 · |01i + a2 · |00i
Wir suchen die Koeffizienten a1 und a2 . Dazu setzen wir in die Schrödingergleichung ein:
a1 E0 · |10i + a2 E0 · |00i + a1 eF · z |10i + a2 eF · z |00i = a1 E (1) · |10i + a2 E (1) · |00i
Wir formen um: Multiplikation mit h10| und h00|, Orthonormierung, Auswahlregeln beachten; das führt
auf die Bestimmungsgleichungen:
a1 · E0 + a2 · eF · h10| z |00i = a1 · E (1)
a2 · E0 + a1 · eF · h00| z |10i = a2 · E (1)
Es gilt h10| z |00i = h00| z |10i = −3 · a0 :
(E0 − E (1) ) · a1 − 3a0 · eF · a2 = 0
(E0 − E (1) ) · a2 − 3a0 · eF · a1 = 0
Hieraus folgt für die neue Energie:
(2)
E2l0 = E0 ± 3a0 · eF
Während für m = ±1 die Energien bei E0 verharren, erhalten wir für m = 0 eine symmetrische
Aufspaltung um E0 herum. Die entsprechenden Wellenfunktionen lauten:
1
1
(1)
(1)
ψ− = √ · (ψ200 + ψ210 ) und ψ+ = √ · (ψ200 − ψ210 )
2
2
Als Beispiel für die Stärke dieses Effektes betrachten wir wiederum eine anliegende Feldstärke F =
10 mV/nm (bei Z = 1). Dann ist ∆k ≈ 12,8 cm−1 , es ergibt sich also eine signifikante Energieänderung.
7.2 Stark-Effekt
Seite 65
7.2.4 Parabolische Koordinaten
Das Lösen der n × n-Matrix von Übergangselementen wird sehr komplex. Zur Vereinfachung gehen wir
in parabolische Koordinaten ξ, η, ψ über:
ξ = r+z
η = r−z
tan ψ = yz
mit
r=
p
x2 + y 2
1. Wir finden zwei neue Quantenzahlen n1 und n2 . Damit ist die Hauptquantenzahl:
n = n1 + n2 + |ml | + 1
2. Die erste Ordnung der Störungsrechnung ergibt:
E (1) = En + 32 a0 · eF ·
n
Z
· (n1 − n2 )
Schwarzschild-Epstein-Formel
(1)
• Die höchste Energie Emax erhalten wir bei n1 = n − 1 und n2 = 0.
(1)
• Die niedrigste Energie Emin erhalten wir bei n1 = 0 und n2 = n − 1.
• Die maximale Energiedifferenz ∆E (1) ist damit:
(1)
(1)
∆E (1) = Emax
− Emin = 3a0 · eF ·
n(n − 1)
Z
• Im asymptotischen Falle n → ∞ ist ∆E (1) ∼ n2 .
• Zum Vergleich: Für n = 5 und Z = 1 mit dem bekannten F ist ∆k = 1280 cm−1 .
3. Die Auswahlregeln müssen (in Analogie zum Zeeman-Effekt) auch für Stark-Übergänge in
parabolische Koordinaten transformiert werden.
• π-Komponente: ∆ml = 0 (linear polarisierte Strahlung k F~ )
• σ-Komponente: ∆ml = ±1 (linear polarisiert für Strahlung ⊥F~ , unpol. für Strahlung k F~ )
4. Die zweite Ordnung der Störungsrechnung ergibt:
¢
3
n
4πε0 · F 2 ³ n ´4 ¡
E (2) = En + a0 · eF · · (n1 − n2 ) −
·
· 17n2 − 3(n1 − n2 )2 − 9|ml |2 + 19
2
Z
16
Z
Der Klammerterm ist immer größer Null, denn n > n1 − n2 und n > |ml |, somit führt E (2) immer
zu einer Energieabsenkung. Diese Ordnung führt also zu einer Rotverschiebung.
7.2.5 Elektrische Feldionisation. Quantenmechanischer Tunneleffekt
Wir gehen wieder aus von einem geraden Coulomb-Potential:
Vc (r) = −
Ze2
4πε0 · |r|
Dazu kommt ein ungerades elektrisches Potential:
Ve (r) = −eF · r
7.2 Stark-Effekt
Seite 66
Das resultierende effektive Potential ist nicht mehr symmetrisch und verhält sich für große r asymptotisch wie das reine elektrische Potential. Ein Grenzfall ist das Gleichgewicht beider Potentiale:
Ze2
= eF · r
4πε0 · r
⇒
r=
eZ
4πε0 · F
Gesucht ist die Hauptquantenzahl nc , oberhalb welcher ein Tunneleffekt sehr Wahrscheinlich wird.
Laut unseren früheren Überlegungen zum H-Atom ergibt sich der Erwartungswert hri aus:
µ
¶
1
a0
a0
2
hril=n−1 = n · 1 +
·
≈ n2 ·
2n
Z
Z
Einsetzen des Gleichgewichtsfalles führt auf:
n4 = n4c =
e5 · Z 3 · m2 1
A
·
=
3
4
F
F
4ε0 · h
⇒
F ∼
1
n4
Oberhalb dieses kritischen Wertes nc sind die Zustände nicht mehr gebunden, da dann der Einfluss
des elektrischen Potentials dominiert. Da das nc stark vom F abhängt, sinkt die Zahl von möglichen
Zuständen (und damit möglichen Übergängen) n in einem Atom mit steigender Stärke des äußeren
Magnetfeldes. Diese Methodik nutzt man in der Spektroskopie, um die Zustände eines Atomes zu
quantisieren.
8.1 Allgemeine Bemerkungen
Seite 67
8 Molekülphysik
8.1 Allgemeine Bemerkungen
8.1.1 Definitionen
Die Atomphysik beschreibt den fundamentalen Aufbau der Atome. Es werden die Wechselwirkungen
zwischen Atomkern und Atomhülle untersucht. Zudem ist hier die Wechselwirkung mit äußeren Feldern
interessant.
Die Molekülphysik gründet auf dem Zusammenschluss von Atomen zu einem Molekül, und widmet
sich chemischen Bindungen von Atomen und deren Stabilität.
Der Begriff des Moleküls kommt vom lateinischen Wort „moles“ (Masse) und beschreibt eine Anordnung von zwei oder mehr Atomen, die durch ihre Wechselwirkung lange genug aneinander gebunden
sind, um eine Einheit zu bilden, die experimentell als solche auch beobachtet werden kann.
Der Molekülbegriff kann durch die Unterscheidung von Makromolekülen verfeinert werden. Diese
Moleküle zeichnen sich durch eine sehr große Masse aus, üblicherweise im Bereich über 108 u (hierbei
ist 1 u = mH die atomare Masseeinheit).
8.1.2 Aufgaben der Molekülphysik
Die Chemie versucht eine Ordnung in die Moleküle zu bringen. Die Aufgabe der Physik ist eine ganz
andere. Sie sucht Antworten unter anderem auf die folgenden fundamentalen Fragen:
• Welche Wechselwirkung ist verantwortlich, dass aus Natrium und Chlor das Molekül Natriumchlorid wird, oder dass aus Sauerstoffradikalen molekularer Sauerstoff wird?
• Wieso kommen O2 , H2 , N2 und so weiter in der Natur nur elementar vor, He hingegen nur
atomar?
• Bindungsenergien ∆Eb ∈ [−10, . . . , −0,01] eV
• Warum ist NaCl polar?
8.1.3 Darstellung von Molekülen
Als erstes betrachten wir die Summenformel, wie zum Beispiel in H2 O, NaCl, CH3 CH2 OH und so
weiter. Desweiteren könne wir auch die Namen angeben:
Summenformel
Name
Strukturformel
H2 O
Wasser
NaCl
CH3 CH2 OH
CH3 OCH3
Natriumchlorid
Ethanol
Dimethylether
Grafiken werden nachgereicht.
8.2 Bindungstypen
Seite 68
8.1.4 Analytik
Spektroskopie: Wir beschießen ein Molekül mit Strahlung der Energie E1 = h · ν1 und können
verschiedene Reaktionen auswerten:
• Absorption, Emmission und Streuung von Strahlung
• Bestimmung von Vibrationen und Rotationen
Mikroskopie: Das Molekül wird abgebildet und können verschiedene Eigenschaften auswerten:
• Anordnung und Struktur von Atomen in Molekülen, Aufbau von Festkörpern
• Aussagen über die Wechselwirkung zwischen zwei Molekülen
8.2 Bindungstypen
Man kann die Bindungen unterscheinden anhand von:
• Bindungsstärke
• Bindungsrichtung
• Bindungsart
Wir unterscheiden folgende Bindungstypen:
1. Kovalente (homöopolare) Bindung – Diese Bindung tritt zum Beispiel bei zwei auf der xAchse lokalisierten Atomen A und B mit px -Orbitalen auf, sofern sich die Orbitale überschneiden.
Die Bindungsenergie ∆Eb ergibt sich aus h ψ1 | ψ2 i und liegt im Bereich von −1 eV bis −10 eV.
Solche gerichteten Bindungen sind insbesondere bei Nichtmetallen, organischen Elementen und
Gasmolekülen interessant.
2. Ionenbindung (heteropolare Bindung) – Diese Bindung entsteht bei dem kompletten Austausch eines Elektrons, zum Beispiel Na + Cl → Na+ + 1e− + Cl− − 1e− → NaCl. Die Atome
werden nun durch die Coulombkraft
Fc =
q1 q2
4πε0 · r2
zusammengehalten. Offensichtlicherweise ist diese Bindung stark gerichtet. Die Größenordnung
der Energie ∆Eb liegt ungefähr zwischen −1 eV und −10 eV. Diese Bindung tritt insbesondere bei
Paaren aus einem metallischen und einem nichtmetallischen Atom auf, sowie in der organischen
Chemie (zum Beispiel bei Carbonsäuren).
3. Metallische Bindung – Diese Bindung entsteht durch das Überlappen der Atomrümpfe mehrerer Atome, sodass die Elektronen delokalisieren (das heißt: das Elektron kann sich im gesamten
Atomverband frei bewegen und ist nicht mehr einem einzelnen Atom zuzuordnen). Die Bindungsenergie liegt zwischen 0 eV und −6 eV, die Bindung ist nicht gerichtet. Metallische Bindungen
treten oft in Metallen und Legierungen sowie in dotierten Polymeren auf.
4. Van-der-Waals-Bindung – Bei allen Elementen interessant ist die van-der-Waals-Bindung,
welche auf „Dipolkräften“ beruht:
• Keesam-Polarisation: Zwei Atome haben magnetische Momente, die miteinander koppeln
(und sich ausrichten).
• Debye-Polarisation: Nur ein Atom besitzt ein Dipolmoment. Das andere Atom besitzt
kein Dipolmoment (zum Beispiel weil alle Schalen voll sind), aber eine Polarisierbarkeit α.
8.3 Modellvorstellungen
Seite 69
• London-Polarisation: Beide Atome haben lediglich eine Polarisierbarkeit, aber durch äußere Einflüsse kommt es auf zufälliger Basis zu einer initialen Ausrichtung, die durch Kopplungseffekte der beiden entstehenden Momente erhalten bleibt.
Die Energie ∆Eb ∼ −1/r6 liegt in der Größenordnung von 0,01 eV bis −0,1 eV. Diese Bindung
ist gerichtet.
5. Wasserstoffbrücken-Bindung: Bei dieser Bindung ist immer ein H-Atom und ein elektronegativer Partner im Spiel. Deren Orbitale überlagern sich quantenmechanisch. Die Energie dieser
gerichteten Bindung liegt bei 0 eV bis −0,5 eV, weshalb innerhalb eines Moleküls diese Bindung
nicht von Relevanz, sie führt aber zu einer Strukturbildung in Molekülverbänden.
8.3 Modellvorstellungen
Wir wollen einige Modelle der Molekülphysik kennenlernen und bewerten.
8.3.1 Kossel-Modell
Kossel ging 1915 von der vollständigen Besetzung (zum Beispiel ns2 np6 ) in Edelgaskonfigurationen
aus.
⊕ Das Modell erklärt die heteropolare Bindung.
⊕ Es enthält die Wertigkeit der Atome. – Die maximale Wertigkeit (Valenz) entspricht der größten
Zahl an aufgenommenen bzw. abgegebenen Elektronen, zum Beispiel:
P + 3H → P3− + 3H+ → PH3
P + 5Cl → P5+ + 5Cl− → PCl5
Somit hat P die Wertigkeit 5.
⊕ Die Löslichkeit eines Moleküls wird korrekt beschrieben. Zum Beispiel hat NaCl in H2 O die
Löslichkeit ε0H2 O ≈ 81 @ OHz . Dadurch verringert sich die Coulombkraft zu:
Fc =
1
q1 · q2
·
4πε0 · ε
r2
Die geringere Coulombkraft begünstigt die Dissoziation in Na+ und Cl− . Analog geht die Lösung
in HCN (Cyanwasserstoff) mit ε0HCN ≈ 95. In Tetrachlorkohlenwasserstoff (mit ε0CCl4 ist die
Löslichkeit jedoch äußerst gering.
ª Diese Modell kann keine polaren Moleküle beschreiben; zum Beispiel wird die Protonenwechselwikrung bei Wasser zwischen den beiden Wasserstoffatomen nicht beachtet.
ª Es sind keine quantitativen Aussagen möglich.
8.3.2 Lewis-Modell
Dieses Modell, benannt nach seinem Entwickler Gordon Newton Lewis (im Jahre 1916), verfeinert
das Kossel-Modell durch die Vorstellung, dass bindende Atome sich mindestens je ein gemeinsames
Elektronenpaar teilen. Unter Berücksichtigung der stabilen Eigenschaften von Edelgaskonfigurationen folgt die sogenannte Oktett-Regel.
8.3 Modellvorstellungen
Molekül
Cl2
H2
HCl
Erstesp p Atom
pp p
Cl
pp
Hp
Hp
Zweites
p p Atom
p Cl pp
pp
pH
pp
p Cl pp
pp
CH4
Hp
p
p Cl p
p
Seite 70
Strukturformel
Cl−Cl
H−H
H−Cl
H
|
H− C −H
|
H
8.3.3 Quantenmechanische Modellvorstellung
Wir betrachten wieder zwei Atome A und B, deren Orbitale sich in einem kleinen Bereich überlappen.
Die Gesamtenergie enthält eine Bindungsenergie:
!
Etot (A + B) = Etot (A) + Etot (B) + ∆Eb ≤ Etot (A) + Etot (B)
Beim Erstellen der Bindung wird der Energiebetrag ∆Eb < 0 an die Umgebung abgegeben. Das Molekül
ist dann stabil. Um die Atome voneinander zu trennen (Dissoziation), muss eine Dissoziationsenergie
∆Ediss = −∆Eb > 0 zugeführt werden. Nun soll die Bindungsenergie quantifiziert werden. Hierzu gibt
es verschiedene Ansätze:
• Valenzstrukturmethode – gut für H2 und ähnliche Moleküle
• Molekülorbitalmethode
Valenzorbitalmethode
Diese Methode wurde 1927 von W. Heitler und F. London entwickelt. Wir machten die Annahme,
dass das Atomorbital zur Beschreibung von kovalenten Bindungen hinreichend gut geeignet ist, das
heißt, wir beschränken uns auf die Störungsrechung in der ersten Ordnung. Betrachtet wird ein H2 Molekül. Die Atome haben einen Abstand r voneinander, der Abstand vom ersten Atom (Index I) zum
ersten Elektron (Index 1) sei rI1 , und so weiter. Das entstehende Vierteilchenproblem ist selbst mit
numerischen Mitteln im Allgemeinen nicht exakt lösbar. Der Hamiltonoperator hat jetzt die Form:
H = H k + H³e
´
~2
~2+∇
~2
Hk = − 2m
·
∇
und
1
2
r
³
2
e
1
Hp = − 4πε
· r1I1 + r1I2 + rII1
+
0
mp +me
mp +m´
e
1
1
r − r12
mr =
1
rII2
−
Die ersten vier Summanden stellen die Elektron-Kern-Wechselwirkung dar. Dazu kommen die KernKern-Wechselwirkung und die Elektron-Elektron-Wechselwirkung. Wir wollen die Schrödingergleichung für eine Welle ψges,0n anwenden:
H · ψges,0n = Eges,0n · ψges,0n
Zur Näherungslösung schlug London vor, die Gesamtenergie nur ale eine Funktion von rI1 und rII2
zu betrachten. Damit reduziert sich der Raum auf sechs Dimensionen, jedoch war immer noch keine
analytische Lösung möglich.
Deshalb macht man einen weiteren Ansatz, nämlich die Born-Oppenheimer-Näherung:
• H-Kerne sind sehr viel schwerer als Elektronen: mp À me , somit ist mr ≈ me
8.3 Modellvorstellungen
Seite 71
• r = const. sei groß
Wir teilen den Hamiltonoperator in einen ungestörten Teil 0 H und eine Störung 1 H. Der Term der
ersten Ordnung der Störungsrechnung für den ungestörten Teil lautet:
µ
¶
e2
1
~2 ³ ~ 2 ~ 2 ´
1
0
· ∇1 + ∇2 −
·
+
H=−
2me
4πε0
rI1 rII2
Der Ansatz für die Lösungsfunktion dieses ungestörten Problems ist:
0
ψges,0n ≈ ψ0n (1, 2) = ψI,0n (x1 , y1 , z1 ) · ψII,0n (x2 , y2 , z2 )
Dies ist eine einfache Zwei-Teilchen-Wellenfunktion, die natürlich Symmetrieeigenschaften aufweisen
muss. Damit sind auch die Energien klar:
0
Eges,0n = En (1) + En (2)
Einsetzen in die Schrödingergleichung liefert:
´
i
h
³
~2
e2
~ 2 · ψI,0n (1) −
·
ψ
(1)
·
∇
+
E
(1)
0 = ψII,0n (2) · − 2m
n
I,0n
1
e
h
³ 4πε02·rI1
´
i
~2
2
~
+ ψI,0n (1) · − 2me · ∇2 · ψII,0n (2) − 4πεe0 ·rII2 + En (2) · ψII,0n (2)
Die nichtriviale Lösung der Gleichung erhält man, wenn die Klammerterme gleich Null sind. Die Energieeigenwerte sind:
0
Eges,0n = 2 · En (1) = 2 · En (2) = 2 · En
−
Aus der Ununterscheidbarkeit von e−
1 und e2 folgern wir eine allgemeine Lösung:
ψ0n (1, 2) = ψI,0n (1) · ψII,0n (2)
ψ0n (2, 1) = ψI,0n (2) · ψII,0n (1)
⇒ ψges,0n = α · ψ0n (1, 2) + β · ψ0n (2, 1)
Aus der Orthonormierung folgt |α|2 + |β|2 = 1. Nun betrachten wir den Störungsterm:
µ
¶
e2
1
1
1
1
1
H=−
+
− −
·
4πε0
rII1 rI2 r r12
Es ist 1 H ¿ 0 H. Aus dem vollständigen Orthonormalsystem 0 ψges,0n und 0 Eges,0n folgt ein neues
Orthonormalsystem bei der Entwicklung in die erste Ordnung der Störungsrechnung. Wir erhalten
ψges,0n = 0 ψges,0n + 1 ψges,0n
und
Eges,0n = 0 Eges,0n + 1 Eges,0n
Die Schrödingerlgeichung lautet dann:
¢
¢ ¡
¢ ¡
¢ ¡
¡0
H + 1 H · 0 ψges,0n + 1 ψges,0n = 0 Eges,0n + 1 Eges,0n · 0 ψges,0n + 1 ψges,0n
Das Resultat für die Eigenwerte ist:
Eges,0n = 2 · En +
C±A
1±S
8.3 Modellvorstellungen
Seite 72
Hierin sind die folgenden Telintegrale enthalten:
R ∗
A = R ψ0n
(1, 2) · 1 Hψ0n (2, 1) dΩ
∗
C = R ψ0n (1, 2) · 1 Hψ0n (1, 2) dΩ
∗ (1, 2) · ψ (2, 1) dΩ
S =
ψ0n
0n
Austauschintegral:
Coulombintegral:
Überlappintegral:
Aus der Eigenwertformel erkennt man, dass es zwei Lösungen gibt, eine symmetrische (+) und eine
antisymmetrische (−):
ψs/as,0 = √
1
2(1+S)
· [ψ0n (1, 2) ± ψ0n (2, 1)]
Die Berücksichtigung des Spins erfolgt über einer Spinor-Funktion:
χ = ψi,0 · δ
Da diese Funktion antisymmetrisch ist (χ(1, 2) = −χ(2, 1)), folgen zwei Lösungen:
χ1 = ψs,0 · δ(»º)
und
χ2 = ψas,0 · δ(»»)
Wenn man also zwei Atome mit parallelem Spin haben, werden sie aufgrund der Pauli-repulsiven
Kraft auseinandergetrieben; sie können also keine Bindung eingehen. Zwei Atome mit antiparallelem
Spin haben hingegen ein Energieminimum der Tiefe ∆Eb = −3,17 eV bei einem stabilen Abstand
r = 1,61 · r0 .
• Aus dieser Überlegung sieht man sofort, dass ein He2 -Molekül nicht stabil sein kann, denn ein
He-Atom hat bereits zwei Elektronen in der Spineinstellung »º. Bringt man ein weiteres HeliumAtom (welches auch wieder zwei Elektronen mit »º hat) an dieses Atom heran, so stoßen sich die
Elektronen mit gleichem Spin sehr stark ab. Dieser Effekt kann nicht durch bindende Elektronen
(also Elektronen mit unterschiedlichem Spin, die noch nicht an ein anderes Elektron gekoppelt
sind) kompensiert werden. Helium-Atome gehen also nie eine Bindung miteinander ein, somit
liegt Helium immer atomar vor.
• Analog erhält man, dass die spontane Verknüpfung H2 + H → H3 nicht möglich ist, da kein
bindendes Elektron vorhanden ist.
• Man kann das Konzept auf beliebige Atome mit Z Elektronen übertragen. Die einzige Bedingung
ist, dass es H- oder He-ähnliche Atome sind. Zum Beispiel sind O + O → O2 und N + N → N2
stabil.
• Betrachten wir die zwei
Atome
qq − q q
···
dung eingehen: N−O
q q – Dieses
zur Zweielektronenbindung nur
qq q q
qq q
Nq und qO.
q q Diese beiden Atome können eine Dreielektronenbin-
System ist stabil. (Die Dreielektronenbindung hat im Vergleich
eine etwa halb so große Bindungsenergie.)
• Ein H+ -Atom kann mit einem H-Atom eine Einelektronenbindung zum Molekül H · H eingehen.
Auch diese Bindung ist etwa um die Hälfte schwächer als die Zweielektronenbindung.
• Zwei Sauerstoffatome koppeln zu einem O2 -Molekül mit Zweielektronenbindung O−O , es gibt
···
−
auch ein O+
2 -Molekül mit Dreielektronenbindung O···O . Ein Ozonmolekül ergibt sich quasi als
Ring aus drei O-Atomen, bei denen jedes Molekül mit jedem eine Zweielektronenbindung eingeht.
8.4 Einige spezielle Bindungen
Seite 73
Molekülstrukturorbitalmethode
Die diskutierte Valenzorbitalmethode wird durch das Vorkommen von Ein- und Dreielektronenbindungen aufgeweicht. Als neuen Ansatz nehmen wir die folgende bessere Näherung:
ψges,0n = [ψI,0n (1) + ψII,0n (2)] · [ψI,0n (2) + ψII,0n (1)]
Die Kreuzterme folgen aus polaren Kräften.
8.4 Einige spezielle Bindungen
Wir haben überlappende Wellenfunktionen. Zur Darstellung versieht man eine der Orbitalseiten mit
einem Minus, die andere mit einem Plus. Das ist natürlich nicht richtig. Allerdings kann beim Vorhandensein eines Partners die Aufenthaltswahrscheinlichkeit des Elektron verschoben werden, sodass die
Nominatur durchaus korrekt wird. Abhängig von der Bindung erhält man zwei Wellenfunktionen:
(
¾
∗ + ψ ψ∗
ψA ψA
ψbin = ψA + ψB
B B
⇒ ψψ ∗ =
∗
∗
ψanti−bin = ψA − ψB
ψA ψB + ψB ψA
8.4.1 π- und σ-Bindungen
Bei den σ-Elektronenbindungen betrachten wir zum Einen zwei Atome mit äußeren s-Orbitalen und
zum Anderen zwei Atome, von denen eines ein s-Orbital und das andere ein pz -Orbital hat. Diese
Orbitale weisen die folgenden Symmetrien auf:
• Drehungen um z-Achse
• Spiegelungen an Ebenen, die die z-Achse enthält
Typische Fälle bei den π-Elektronenbindungen sind die Überlappung von px - mit s- oder px - mit
px -Orbitalen. Diese Systeme haben die folgende Symmetrie:
• Änderung des Vorzeichens bei Spiegelung an einer Ebene durch die z-Achse, senkrecht zur Achse,
entlang welcher die Orbitale ausgerichtet sind
Anmerkungen:
• s-Elektronen sind kugelsymmetrisch. Zwischen ihnen gibt es also nur σ-Bindungen.
• Bei 2p-Elektronen unterscheidet man pz -Orbitale (Rotationssymmetrie in Bezug auf z-Achse;
somit σ-Bindung) und px - bzw. py -Orbitale (keine solche Symmetrie; somit π-Bindung).
• Ähnlich muss man bei d- und f -Elektronen unterscheiden.
• Die π-Bindung ist viel schwächer als die σ-Bindung, da das Überlappungsgebiet kleiner ist.
• Der σ-Anteil einer Bindung sorgt für ihre Stärke, der π-Anteil für Drehungshemmung. Dies wird
zum Beispiel bei Ethin (H−C−
−C−H) deutlich werden.
• Die Mischung aus π- und σ-Bindungen sorgt für die Winkelstrukturen in Molekülen. Betrachte
zum Beispiel Wasser (H−O−H).
O : 1s2 (»º)2s2 (»º)2p2z (»º)2px (»)2py (»)
Der Winkel zwischen den H-Atomen liegt bei 104◦ 270 . Die Abweichung entsteht durch das Eigenvolumen der Atome, Coulomb- und Zentrifugalkräfte.
8.4 Einige spezielle Bindungen
Seite 74
• Gleiches gilt natürlich auch für SO2 , NO2 und H2 S. Wir vergleichen H2 O und H2 S wegen:
^(H−S−H) < ^(H−O−H)
wegen
dAtom,S > dAtom,O
Tatsächlich beträgt der Winkel beim H2 S nur 92◦ .
8.4.2 Hybridisierung
Wir fangen mit dem Beispiel des Be-Atoms an. Die Besetzung ist wie eine Edelgaskonfiguration:
Be : 1s2 (ȼ)2s2 (ȼ)
Be ist zweiwertig. Geht das Atom eine Bindung ein, so verändert sich die Konfiguration zu:
Be : 1s2 (»º)2s(»)2p(»)
Hiermit haben wir zwei Elektronen, die eine Bindung eingehen können. Dieser Vorgang heißt Hybridisierung. Ganz äquivalent funktioniert das mit Kohlenstoff:
C : 1s2 (»º)2s2 (»º)2p2 (»»)
Hieraus erwartet man zunächst, dass Kohlenstoff zweiwertig ist, denn es gibt zwei bindungsfähige
Elektronen. Zum Beispiel beim Methan aber geht Kohlenstoff vier Bindungen ein. Das erklärt sich
durch die Hybridisierung zu:
C : 1s2 (»º)2s(»)2p3 (»»»)
Die Ursache für Hybridisierungsvorgänge ist der Einfluss der Bindung auf innere Elektronen. Wir
betrachten zum Beispiel ein 2s2 -Elektron im Kohlenstoff. Um in eine molekulare Bindung einzugehen
(was eine geringere Energie bedeuten würde), muss es zunächst eine bestimmte zusätzliche Energie, die
Promotionsenergie aufbringen. In unserem Falle hat diese den Wert EPr = 4,2 eV. Es muss gelten:
|EPr | < |∆Eb |
Als Beispiel betrachten wir Helium:
He : 1s2 (»º) + EPr −→ 1s(»)2s(»)
Wir hätten also eine neue Bindung mit 1s2s, aber hier ist |EPr | > |∆Eb |, deshalb promoviert Helium
nie. Dieses Beispiel ist also langweilig, wir gehen deshalb zurück zum Kohlenstoff mit seiner sp3 Hybridisierung:
C : 2s(»)2px (»)2py (»)2pz (»)
Es ergeben sich damit auch vier Wellenfunktionen ψ(2s), ψ(2px ), ψ(2py ) und ψ(2pz ). Sie repräsentieren
die folgenden Hybridzustände:
h
i
ψ1 = 21 · ψ(2s) + ψ(2px ) + ψ(2py ) + ψ(2pz )
h
i
ψ2 = 12 · ψ(2s) + ψ(2px ) − ψ(2py ) − ψ(2pz )
h
i
ψ3 = 12 · ψ(2s) − ψ(2px ) + ψ(2py ) − ψ(2pz )
h
i
ψ4 = 12 · ψ(2s) − ψ(2px ) − ψ(2py ) + ψ(2pz )
Diese neuen Wellenfunktionen in der sp3 -Hybridisierung sind vollständig und orthogonal. Da die ψi
gleichwertig sind erhält man eine Tetraederstruktur. In dieser gewinkelten Struktur beträgt der Winkel
8.5 Einige spezielle Bindungen
Seite 75
zwischen den H-Elektronen gerade 109◦ 280 . Die ⊕- und ª-Anteile sind unterschiedlich stark. Den
Energieaufwand für die Hybridisierung bezeichnet man mit EHy . Betrachtet man das Kohlenstoffatom
weiterhin, so erkennt man, dass die inneren 1s2 -Elektronen sich nicht an der Bindung beteiligen. Das
liegt an der zu hohen Bindungsenergie.
Die folgende Tabelle fasst Hybridisierungen bei einigen wichtigen Atomen zusammen:
Atom
C
Si
Ge
Grundzustand
2s2 (»º)2p2 (»»)
3s2 (»º)3p2 (»»)
4s2 (»º)4p2 (»»)
Art der Hybridisierung
sp3 -Hybridzustand im Bulk
sp3 -Hybridzustand
sp3 -Hybridzustand
Hybridisierte Besetzung
2s(»)2p3 (»»»)
3s(»)3p3 (»»»)
4s(»)4p3 (»»»)
Die Atome Ge und Si sind wichtige Halbleiter, während C ein fundamentales Element für die organische
Chemie ist. Die Elemente unterscheiden sich also mitunter stark in ihren äußeren Eigenschaften, haben
aber das gleiche Bindungsverhalten.
Im Allgemeinen ist eine Hybridisierung immer dann sinnvoll, wenn durch die zusätzliche Bindungsenergie ein energetisch niedrigerer Zustand erreicht werden kann. Deswegen ist die Hybridisierung besonders
bei vierwertigen Atomen besonders relevant.
sp2 -Hybridisierung
Analog zur sp3 -Hybridisierung können wir auch die sp2 -Hybridisierung betrachten. Im Allgemeinen ist
dies der folgende Hybridisierungsprozess:
+E
ns2 (»º)np1 (») −−−Pr
→ ns1 (»)np2 (»»)
Wir können sofort die Wellenfunktion
q
1
ψ1 =
q3
1
ψ2 =
q3
1
ψ3 =
3
aufschreiben:
q
· ψ(ns) + 23 · ψ(npx )
q
q
1
· ψ(ns) − 6 · ψ(npx ) + 12 · ψ(npy )
q
q
· ψ(ns) − 16 · ψ(npx ) − 12 · ψ(npy )
Wiederum sind die Wellenfunktionen gleichwertig, die hybridisierten Orbitale ordnen sich nun in einem
gleichseitigem Dreieck an. Ein wichtiges Beispiel für sp2 -Hybridisierung liefern die Kohlenstoffatome
im Bulk eines Graphitkristalls.
sp-Hybridisierung
Wir haben nun den Hybridisierungsprozess:
+E
ns2 (»º) −−−Pr
→ ns1 (»)np1 (»)
Die hybridisierten Wellenfunktionen hierzu lauten:
h
i
ψ1 = √12 · ψ(2s) + ψ(2px )
h
i
ψ2 = √12 · ψ(2s) − ψ(2px )
2
3
Ein Beispiel ist hierfür ist das Ethin-Molekül H−C−
−C−H. Neben den eingeführten sp-, sp - und sp 2
2
2
Hybirdisierungen existieren noch mehr Möglichkeiten, zum Beispiel sp d- und sp d -Hybridisierung.
(Diese Vorgänge führen zu quadratischer bzw. oktaedrischer Symmetrie.)
8.5 Mehrfachbindungen. Mesomerie
Seite 76
8.5 Mehrfachbindungen. Mesomerie
Wir betrachten die Bindungen am Beispiel mit dem Kohlenstoffatom und der sp-, sp2 - und sp3 Hybridisierung:
H H
1.
Ethan: C2 H6 : H3 C−CH3 – Einfachbindung mit sp3 -Hybrisierung
2.
Ethen: C2 H4 : H2 C−CH2 – Doppelbindung mit sp2 -Hybrisierung
3.
Ethin: C2 H2 : HC−
−CH – Einfachbindung mit sp-Hybrisierung
H
C C
H
H H
HH
H
C C©
HH
H©
H
C C
H
Hier haben wir kein Dipolmoment, weil die Hybridisierungen symmetrisch sind und gleiche Substituenten haben. (Man erhält ein Dipolmoment zum Beispiel, wenn man ein H-Atom durch ein D-Atom
ersetzt.) Wir wollen die Dipolmomente in einer Tabelle darstellen:
Molekül
p~[1030 Cm]
Molekül
p~[1030 Cm]
CH3
0
H2 O
6,34
C2 H6
0
HCl
3,47
C2 H4
0
KCl
21,32
C2 H2
0
KBr
30,29
CCl4
0
CsI
34,36
C6 H 6
0,27
O2
0
H2
0,07
Untersuchung der Mesomerie am Beispiel Benzen
Wir betrachten Mesomerie und Resonanzen bei Benzen (C6 H6 ).
• Kekulé 1865: Das Benzen besteht aus einem Ring aus Kohlenstoffatomen mit abwechselnden
Doppel- und Einfachbindungen, daraus ergeben sich zwei mögliche Formen ψK1 und ψK2 .
• Devar 1866: Man erhält eine weitere mögliche Form, indem man zwei gegenüberliegende Doppelbindungen hat und eine weiter Bindung zwischen zwei gegenüberligenden Kohlenstoffatomen.
Daraus ergeben sich weitere drei Permutationen (ψD1 , ψD2 und ψD3 ).
• Ingold 1933: qu.mech. Behandlung (mit Störungsrechnung); für alle Lewis-Darstellungen gilt:
– Gesamtwellenfunktion ψBenzen = c1 · (ψK1 + ψK2 ) + c2 · (ψD1 + ψD2 + ψD3 ) mit c1 = 0,624
und c2 = 0,270 – Die Mischung der Wellenfunktionen bezeichnet man als Mesomerie.
– σ-Bindungen zwischen C−C und C−H
– π-Bindungen senkrecht zur Molekülebene ausgerichtet; Delokalisation → Entstehung von
Elektronenwolken parallel zur Molekülebene
Die π-Elektronen führen zu einer neuen physikalischen Eigenschaften:
~ hat senkrecht zur Molekülebene einen großen Einfluss, jedoch einen sehr
1. Diamagnetismus: H
kleinen bei Ausrichtung parallel zur Molekülebene.
~ j beschriebene induzierte Polarisation gilt die
2. Polarisierbarkeit: Für die durch αij = ∂ P~i /∂ E
Relation αxx = αyy = 2 · αzz . In der Molekularelektronik nutzt man dies, indem mehrere Benzenmoleküle hintereinander „gestapelt“ und in ein elektrisches Feld gebracht werden. Das führt zu
einer Anisotropie in den elektrischen Eigenschaften (δij -anisotrope Leitfähigkeit): Es resultiert
eine hohe Leitfähigkeit parallel zur xy-Ebene, einen kleine Leitfähigkeit entlang der z-Richtung
8.7 Rotations- und Schwingungsniveaus in Molekülen
Seite 77
3. Mesomerie in kettenförmigen Kohlenwasserstoffmolekülen: Dieses Molekül schreibt man wie folgt.
"
#
|
−C −C−
|
n
Man spricht von einer konjugierten Doppelbindung, diese führt zu hoher Leitfähigkeit. Polymere wie Polyacetylen erhalten durch Dotierung mit Ionen ein um zehnfach bessere Leitfähigkeit
als Kupfer.
8.6 Bindungsverhältnisse in Festkörpern
Man wendet hier das LEGO-Prinzip an, das bedeutet: Atomare Elemente und deren Wellenfunktionen werden zu σ- und π-Bindungen hybridisiert und man erhält massgeschneiderte Eigenschaften.
Bindungsart
metallische Bindung
van-der-WaalsBindungen
van-der-WaalsBindungen
Ionenbindung
Beispiel
Na, Mg, Fe, Legierungen
He, Ne, Ar
Kovalente Bindung
C, Ge, Si
H2 , N2 , O2 , HCl, H2 O
NaCl, CsCl, ZnS, TiO2 , CaF2
Elektronenverteilung
immer delokalisiert
kugelsymmetrisch (σ-Charakter),
am Atom lokalisiert
kugelsymmetrisch, am Molekül lokalisiert
kugelsymmetrisch,
am Ion lokalisiert
zwischen zwei Atomen lokalisiert
Hybridwellenfunktionen
für große Abstände: Kugelsymmetrie
8.7 Rotations- und Schwingungsniveaus in Molekülen
In einem Atom konnte ein Elektron sich auf verschiedenen Energieniveaus bewegen. Ähnlich kann man
das auch für Moleküle angehen. Zum Beispiel können die Elektronen in einer Bindung zwischen einem
Atom A und und einem Atom B auch verschiedene Niveaus unter Aufnahme oder Abgabe von Energie
einnehmen. Wir haben also:
• atomare Übergänge innerhalb der Atome A und B
• Schwingungen und Vibrationen zwischen den Atomen
• Rotation um das Molekül AB
Atomare Spektren weisen immer scharfe Linien auf, hingegen habe molekulare Spektren breite Linien;
es gibt also viele ähnliche Niveaus, die zu Bändern zusammengefasst werden. Die grobe Struktur
des Spektrums resultiert aus atomaren Übergängen (Abstände im eV-Bereich), die Aufspaltung der
Linien zu Bändern ist durch die Schwingungen und Rotationen im Atom bedingt (Abstände im meVBereich).
8.7 Rotations- und Schwingungsniveaus in Molekülen
Seite 78
Rotationsenergieniveaus
Wir nehmen wieder zwei Atome m1 und m2 und lassen das Molekül um seinen Schwerpunkt S rotieren.
Die Atome haben dazu einen Abstand r1 und r2 , wobei r0 = r1 + r2 ist. Wir können schreiben:
1
Erot = I · ω 2
2
~ = I ·~
Es ist ω die Kreisfrequenz und I das Trägheitsmoment. Aus der klassischen Physik ist L
ω bekannt.
Damit entsteht:
~2
L
~ 2 = J(J + 1) · ~2
Erot =
mit L
2I
~ war aus der Atomphysik bekannt. Wir führen eine neue Quantenzahl J als BahndrehimpulsDas L
quantenzahl des Moleküls ein. Damit haben wor für die Rotationsenergie
Erot =
J(J + 1) · ~2
=: J(J + 1) · B
2I
So können wir das Trägheitsmoment, damit die Bindungslängen messen und somit das Molekül bestimmen. Für ein zweiatomiges Molekül ergibt sich (mit m1 · r1 = m2 · r2 für den Schwerpunkt):
I = m1 · r12 + m2 · r22 = µ · r02
Beispiel 8.1
HCl-Molekül
m1
m2
µ
= mCl = 35,5 u
= mH = 1 u
≈ 0,982 u
Nun sei die Bindungslänge ≈ 0,1 nm =
b 1Å. Damit kann man B sofort ausrechnen:
I = µ · r02 ⇒ B =
~2
≈ 2,6 · 10−4 eV = 0,26 meV
2I
Zum Vergleich betrachten wir die thermische Anregung: kB · T = kB · 300 K ≈ 26 meV
Auch für Rotationsübergänge in Molekülen gibt es Auswahlregeln.
∆J = ±1
und
∆Erot = EJ − EJ−1 =
~2
~2 ~2
· [J(J + 1) − (J − 1)J] =
·
·J
2I
2I I
Zusammengefasst gilt:
∆J = ±1
und
∆Erot =
~2
I
·J
Für die Analyse nutzt man zum Beispiel Infrarotspektrometer, bestimmt B und erhält damit Informationen über Masse, Bindungslänge und Rotationsenergie.
8.7 Rotations- und Schwingungsniveaus in Molekülen
Seite 79
Schwingungsenergieniveaus
Wir stellen uns vor, die Moleküle seien mit einer Feder verbunden. Hierbei entspricht die Federkonstante
k der Stärke der chemischen Bindung. Da die Schwingungsenergie in meV-Bereich ist, approximiert
man das Potential als ein harmonisches. Die Amplitude der Schwingung soll bei ungefähr ∆r < 0,02 nm
liegen, dabei haben wir einen Abstand von r = 0,74 nm. Die Schwingungsamplitude beträgt also rund
3% des Abstandes. Damit stellt die Betrachtung des harmonischen Oszillators eine gute Näherung
dar.
µ
¶
1
Evibr = n +
· ~ω
2
Aus der Mechanik kennen wir:
1
f =ν=
·
2π
s
k
µ
Das Eigenwertproblem des quantenmechanischen Oszillators ist bereits gelöst, daraus ergeben sich die
folgenden Auswahlregeln:
∆n = ±1
∆Evibr = En − En−1 = ~ω
Wir schätzen die Größenordnung der Energie ab:
ν ≈ 5 · 1013 Hz
Beispiel 8.2
⇒
∆Evibr ≈ 0,2 eV ≈ 8 · kB · T ≈ 1000 · Erot
CO-Molekül
Wir haben hier eine Frequenz von ν = 6,42 · 1013 Hz. Mit den Massen m1 = mC = 12 u und m2 = m= = 16 u.
Damit ist k ≈ 1,86 · 103 N/m.
Kombinierte Rotations- und Schwingungszustände
Es muss für die Übergänge gelten:
∆J = ±1
und
∆n = ±1
Der Übergang ist also von einem Niveau |n, Ji zu |n ± 1, J ± 1i. Wir betrachten nun die Zielzustände
|n − 1, J − 1i oder |n + 1, J + 1i. Die Energien dieser Übergänge ist:
(
2
hν + (J + 1) · ~I ∆J = +1
∆E = ∆Evib + ∆Erot =
2
hν + J · ~I
∆J = −1
Wir regen das Molekül mit Photonen veränderlicher Energie an. Um die Frequenz ν herum ordnen
sich Peaks an, die die einzelnen Übergänge repräsentieren. Die Übergänge mit ∆J = −1 ergeben den
P-Zweig (die Energie der Photonen ist hier kleiner als hν, weil Energie beim Übergang in den höheren
Zustand absorbiert wird), die Übergänge mit ∆J = 1 bilden den R-Zweig (hier ist die Energie der
Photonen größer als hν).
8.7 Rotations- und Schwingungsniveaus in Molekülen
Seite 80
Rotations-Vibrations-Spektren bei gleichzeitiger Anregung der
Elektronenzustandes. Franck-Condon-Prinzip
Im Allgemeinen tauchen alle drei Potentiale gleichzeitig auf: Wir haben in so einer Situation ein
Lennard-Jones-Potential. Franck und Condon haben festgestellt, dass man in der Nähe des
Grundzustandes das Potential als Parabel (Potential eines harmonischen Oszillators) annähern kann.
Damit konnten sie die Aufenthaltswahrscheinlichkeit für verschiedene n bestimmen.
Vom Grundzustand (n = 0, 1, 2, 3, . . .) geht man durch Anregung in einen angeregten Zustand (n0 =
0, 1, 2, 3, . . .) über. Die Aufenthaltswahrscheinlichkeit der Elektronen ist für n, n0 = 0 in der Mitte, und
für n, n0 À 0 am Rand am Größten. Somit sind die folgenden Übergänge für Anregung und Abregung
denkbar:
• Anregung (Absorption): n = 0 → n0 À 0
• Abregung (Emission): n0 À 0 → n = 0
Folglich hat ein Molekül im angeregten Zustand einen größeren Abstand zwischen den Elektronen und
damit die höhere Energien.
Rotations- und Schwingungsspektren mehratomiger Moleküle
Wir betrachten Moleküle mit N ≥ 3 Atomen. Die Anzahl der Freiheitsgrade ist f = 3N − 3 (durch
Translation und Rotation). Bei linearen Molekülen reduzieren sich die Freiheitsgrade auf f = 3N −
5. Im Fall von genau drei Atomen in linearer Anordnung (Beispiel: CO2 ) erhält man also f = 4
Normalschwingungen:
• Valenzschwingung (Streckschwingung)
←
−
→
−
– Ultrarot-inaktive Schwingung: O −C− O
←
− →
− ←
−
– Ultrarot-aktive Schwingung: O − C − O mit νS1 = 2349,3 cm−1
• Deformationsschwingung (Knickschwingung): O↓ −C↑ −O↓ und O¯ −C⊗ −O¯
– entartet, da sich nur die Raumrichtung unterscheidet
– Frequenz: νS2 = 667,3 cm−1
νs1 und νs2 entsprechen quantenmechanischen Übergängen, bei denen eine Dipolanregung vorliegt.
Linear polarisiertes Licht:
h u1 | zu2 i
Zirkular plarisiertes Licht: h u1 | (x + iy)u2 i
Raman-Spektroskopie
Die Ultrarot-inaktive Valenzstreckschwingung entspricht keinem Dipolübergang, sie bewirkt aber eine
Änderung der Bindungsstärken. Damit kann man eine Polarisierbarkeit angeben:
~
µ
~ ind = α · E
mit
α=
∂ P~i
= (αij )
~j
∂E
Für diese Entdeckung erhielten A. G. Smekal und C. Raman 1930 den Nobelpreis.
~ =E
~ 0 · cos ω0 t führt zu einer Modulation der Ortskoordinate:
Eine äußere Anregung E
xvib = x0 · cos ωvib t
8.7 Rotations- und Schwingungsniveaus in Molekülen
Seite 81
Die Polarisierbarkeit α wird ebenfalls moduliert. Dazu machen wir eine Taylorentwicklung:
¯
∂ α ¯¯
α = α0 +
· xvib + O(α2 )
∂xvib ¯xvib =0
Einsetzen liefert das magnetische Moment:
¯
∂α ¯
~ 0 · cos ωvibr t · cos ω0 t
~
·E
µ
~ ind = α0 · E + ∂xvib ¯
xvib =0
¯
i
h
~0
x0 · E
~ 0 · cos ω0 t + ∂ α ¯¯
= α0 · E
+
cos(ω
−
ω
)t
·
·
cos(ω
+
ω
)t
0
0
vib
vib
∂xvib x =0
2
| {z }
{z
} |
{z
}
|
vib
Rayleigh-Peak
Stokes-Peak
Anti-Stokes-Peak
Die entsprechenden Peaks ergeben sich bei der Raman-Spektroskopie, bei welcher das Molekül
entsprechend der obigen Formel in virtuelle Energieniveaus an- und abgeregt wird. Fällt ein virtuelles
Niveau mit einem atomaren Niveau zusammen, so ist die Raman-Spektroskopie resonant. Weiterhin
sehen wir:
• Die Stokes-Linien sind immer die stärksten, da sie (anders als die Anti-Stokes-Linien) vom Grundzustand ausgehen, welcher stärker bevölkert ist.
• Raman- und Infrarotspektroskopie sind komplementär (siehe zum Beispiel CO2 ).
• Physikalisch interpretiert man die Raman-Spektroskopie als Seitenbandmodulation.
Stichwortverzeichnis
Seite 82
Stichwortverzeichnis
Sonderzeichen
π-polarisiertes Licht . . . . . . . . . . . . . . . . . . . . . . . . 57
σ-polarisiertes Licht . . . . . . . . . . . . . . . . . . . . . . . . 57
d-Wellenfunktion . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
p-Wellenfunktion . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
s-Wellenfunktion . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
sp3 -Hybridisierung . . . . . . . . . . . . . . . . . . . . . . . . . 73
Übergangsdipolmatrixelement . . . . . . . . . . . . . . 37
Übergangselement . . . . . . . . . . . . . . . . . . . . . . . . . . 51
Übergangsfrequenz . . . . . . . . . . . . . . . . . . . . . . . . . 37
Bohrsche Radius . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
A
Abregung. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .9
Actinoide. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .51
Alkaliatom . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 52
anisotrope Leitfähigkeit. . . . . . . . . . . . . . . . . . . . .75
Anregung. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .9
Apertur . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
Assoziierte Laguerre-Polynome . . . . . . . . . . . . . 16
Atomare Masseeinheit . . . . . . . . . . . . . . . . . . . . . . 66
Atomkern . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
Atomphysik . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 66
Aurora-Linie . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 54
Auswahlregeln . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37
B
Bänder . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 76
Babinet-Prinzip . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
Bahndrehimpulsquantenzahl . . . . . . . . . . . . . . . . 15
Bahndrehimpulsquantenzahl eines Moleküls . 77
Boson . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 45
Bra-Vektor . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29
Bulk . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
Einstein-Koeffizient . . . . . . . . . . . . . . . . . . . . . . . . . 40
Eisengruppe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 51
elektrischer Dipoloperator . . . . . . . . . . . . . . . . . . 36
Elektronenaffinität . . . . . . . . . . . . . . . . . . . . . . . . . 54
Elektroneneinfang . . . . . . . . . . . . . . . . . . . . . . . . . . 10
Elektronenkonfiguration . . . . . . . . . . . . . . . . . . . . 17
Elektronenspin . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
Entartung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
Erweiterte Auswahlregeln. . . . . . . . . . . . . . . . . . .38
Erzeugungsoperator . . . . . . . . . . . . . . . . . . . . . . . . 31
F
Feldionenmikroskop. . . . . . . . . . . . . . . . . . . . . . . . . .4
Fermion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 45
Frequenzmodulation . . . . . . . . . . . . . . . . . . . . . . . . 57
G
Grundzustand . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32
H
Hamilton-Operator . . . . . . . . . . . . . . . . . . . . . . . . . 13
Hartes Potential . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34
Hauptquantenzahl . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
Heisenberg . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 50
Heisenberg’sche Unschärferelation . . . . . . . . . . 30
Hermitesche Polynome . . . . . . . . . . . . . . . . . . . . . 32
Hundsche Regeln . . . . . . . . . . . . . . . . . . . . . . . . . . . 50
Hybridisierung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 73
Hybridzustand . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 73
D
Debye-Polarisation: . . . . . . . . . . . . . . . . . . . . . . . . . 67
Diamagnetismus . . . . . . . . . . . . . . . . . . . . . . . . . . . . 60
Dirac-Gleichung . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
Dissoziation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 69
I
Identitätsoperator . . . . . . . . . . . . . . . . . . . . . . . . . . 29
Imaging . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
Infrarotspektrometer . . . . . . . . . . . . . . . . . . . . . . . 77
Inlet. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .4
Interkombinationsübergang . . . . . . . . . . . . . . . . . 53
Intersystem-Crossing . . . . . . . . . . . . . . . . . . . . . . . 49
Ionenbindung (heteropolare Bindung). . . . . . .67
Ionisation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 54
Ionisationsenergie. . . . . . . . . . . . . . . . . . . . . . . . . . . .9
E
Edelgaskonfiguration . . . . . . . . . . . . . . . . . . . . . . . 68
K
Kaskade . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 55
Stichwortverzeichnis
Keesam-Polarisation: . . . . . . . . . . . . . . . . . . . . . . . 67
Ket-Vektor . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29
Kollaps . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30
Konjugierte Doppelbindung. . . . . . . . . . . . . . . . .76
Korrespondenzprinzip . . . . . . . . . . . . . . . . . . . . . . . 7
Kovalente (homöopolare) Bindung . . . . . . . . . . 67
Kugelfunktion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
L
Lamb-Shift . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23
Landau-Niveau . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 61
Lanthanoide . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 51
Laser . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
Legendre-Polynom. . . . . . . . . . . . . . . . . . . . . . . . . .15
LEGO-Prinzip. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .76
Lennard-Jones-Potential . . . . . . . . . . . . . . . . . . . . 79
Lineare Superposition . . . . . . . . . . . . . . . . . . . . . . 30
London-Polarisation: . . . . . . . . . . . . . . . . . . . . . . . 68
M
Magnetische Quantenzahl . . . . . . . . . . . . . . . . . . 15
Makromolekül . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 66
Mesomerie. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .75
Metallische Bindung . . . . . . . . . . . . . . . . . . . . . . . . 67
Mikroskopie: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 67
Molekül . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 66
Molekülphysik . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 66
O
Oktett-Regel . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 68
Ortho-Helium . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 49
P
P-Zweig . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 78
Palladiumgruppe . . . . . . . . . . . . . . . . . . . . . . . . . . . 51
Para-Helium. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .49
Platingruppe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 51
Promotionsenergie . . . . . . . . . . . . . . . . . . . . . . . . . . 73
Q
Quantendefekt . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 52
R
R-Zweig . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 78
Raman-Spektroskopie . . . . . . . . . . . . . . . . . . . . . . 80
Rastersondenmikroskop . . . . . . . . . . . . . . . . . . . . . . 5
Rastertunnelmikroskop . . . . . . . . . . . . . . . . . . . . . . 5
Rotverschiebung . . . . . . . . . . . . . . . . . . . . . . . . . . . . 64
S
Singulett . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 47
Seite 83
Spektroskopie . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
Spektroskopie: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 67
Sphärische Kugelfunktion . . . . . . . . . . . . . . . . . . . 15
Spindrehimpuls . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
Spineinstellung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
Spinor . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 48
Spinquantenenergie . . . . . . . . . . . . . . . . . . . . . . . . . 19
Spinquantenzahl . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
Summenformel . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 66
T
Tauchbahn . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 52
Termwert . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10, 52
Transmissionselektronenmikroskop . . . . . . . . . . . 5
Triplett . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 47
Tunnelmikroskop . . . . . . . . . . . . . . . . . . . . . . . . . . . 36
V
Vakuumpolarisation . . . . . . . . . . . . . . . . . . . . . . . . 24
Valenz . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 68
Van-der-Waals-Bindung . . . . . . . . . . . . . . . . . . . . 67
Vernichtungsoperator . . . . . . . . . . . . . . . . . . . . . . . 31
W
Wasserstoffbrücken-Bindung: . . . . . . . . . . . . . . . 68
Z
Zustandsdichte . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5