Versuch EL-V3: Halbleiterdioden

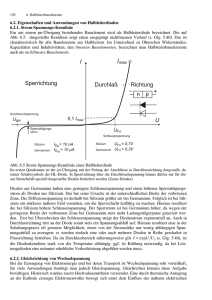
Versuch EL-V3: Halbleiterdioden
Inhaltsverzeichnis
1
Einleitung
2
2
Grundlagen der pn-Diode
2
3
Grundlagen der Solarzelle
8
4
Messaufbau
10
5
Vorbereitungsfragen
12
6
Messaufgaben
13
Literaturverzeichnis
14
2.1 pn-Übergang . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.2 I -U -Kennlinie . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
EL-V3 - 1
2
4
1 Einleitung
Im folgenden Versuch sollen die Kennlinien einer Gleichrichter-Diode mit und ohne Serienwiderstand, einer Zener-Diode und eines Moduls aus fotovoltaischen Zellen analysiert und
mit den idealen analytischen Kennlinien verglichen werden.
Am Anfang dieses Praktikumsversuches wird eine Vorbesprechung stattnden. Während
dieser Vorbesprechung sollten Sie in der Lage sein, die Vorbereitungsfragen (Kapitel 5)
sowie weitere Verständnisfragen zum Text selbständig zu beantworten und den verwendeten
Messaufbau erklären zu können. Die Teilnahme am Versuch kann Ihnen bei einer nicht
ausreichenden Vorbereitung verweigert werden. Die vorliegende Praktikumsanleitung ist
somit vor dem Versuchsbeginn vollständig durchzulesen. Im zweiten Abschnitt werden die
Messwerte für die einzelnen Bauelemente mittels einer von einem Lab-View Programm gesteuerten Source-Measurement-Unit (SMU - Quellenmessgerät) von Keithley aufgenommen.
Im letzten Abschnitt erfolgt die Darstellung und Auswertung der Messwerte mit Hilfe des
Programms Origin.
In dieser Praktikumsanleitung werden zunächst die Grundlagen des pn-Übergangs für das
Bauelement der Diode kurz wiederholt. Für eine ausführliche Aufarbeitung der Grundlagen
sollten Sie Ihre alten Aufzeichnungen der Vorlesungen Elektronische Materialien (2. Semester) und Elektronische Bauelemente (3. Semester) oder auch die im Anhang angegebene
Literatur benutzen. Im Kapitel 3 wird die fotovoltaische Zelle (Solarzelle) näher behandelt,
da diese in den Vorlesungen nicht bzw. unzureichend behandelt wurde. Danach wird der
Versuchsaufbau (Kapitel 4) vorgestellt and dem sich die Vorbereitungsfragen (Kapitel 5)
anschieÿen. Zum Schluss stehen die von Ihnen durchzuführenden Messungen (Kapitel 6).
2 Grundlagen der pn-Diode
2.1
pn-Übergang
Wie der Name schon sagt, bestehen pn-Dioden aus zwei angrenzenden und verschieden dotierten Halbleiterbereichen, wobei als Grundmaterial für den Halbleiter (HL) häug Silizium
(Si) verwendet wird. Ein Bereich weist eine Löcherleitung (p-Dotierung) und der andere
Bereich eine Elektronenleitung (n-Dotierung) auf. Eine p-Dotierung wird erreicht wenn in
das Gitter des Halbleiters Akzeptoren eingebaut werden, also Fremdatome, die ein Elektron
weniger auf der äuÿeren Sphäre besitzen als die Atome des Halbleiters. Bei Si lässt sich
dies z.B. durch das Einbringen von Boratomen (B) erreichen. Bei einer p-Dotierung wird
angenommen, dass die durch die Dotierung entstandenen frei beweglichen Löcher für den
Ladungsträgertransport verantwortlich sind. Eine n-Dotierung liegt vor, wenn einzelne Atome des Halbleiters durch Donatoren ersetzt werden, also wenn die eingebauten Fremdatome
ein Elektron mehr auf der äuÿeren Sphäre besitzen als die Atome des Halbleiters. Durch
Phosphor (P) z.B. lässt sich Si n-dotieren. Bei einer n-Dotierung wird angenommen, dass
die durch die Dotierung entstandenen frei beweglichen Elektronen für den Ladungsträgertransport verantwortlich sind.
An der Grenzschicht zwischen den beiden Bereichen diundieren die beweglichen Löcher
in das n-Gebiet und die beweglichen Elektronen in das p-Gebiet. Hierdurch hinterlassen
die beweglichen Ladungsträger feste, ionisierte Atomrümpfe. Im p-Gebiet sind die AtomEL-V3 - 2
rümpfe negativ und im n-Gebiet positiv geladen. Ein internes elektrisches Feld entsteht,
welches der Diusion von Elektronen und Löchern entgegenwirkt. Es stellt sich ein Gleichgewichtszustand ein. Der Bereich, in der die freien Ladungsträger verarmt sind, wird als
Raumladungzone (RLZ) bezeichnet. Der Gleichgewichtszustand ohne angelegter äuÿerer
Spannung UF = 0 ist in Bild 1(a) als Querschnitt und in Bild 1(b) im Bänderdiagramm
veranschaulicht.
Bild 1: (a) Schaltsymbol einer pn-Diode und der zugehörige Querschnitt für UF = 0.
(b) Bänderdiagramm eines pn-Übergnags für UF = 0.
Die innere Barrierenhöhe beträgt eUD bei einem pn-Übergäng ohne äuÿere Spannung
UF . Mit angelegter Spannung ändert sich die Barrierenhöhe wie folgt: e(UD − UF ). Die Diffusionsspannung UD hängt von der intrinsichen Ladungsträgerdichte ni , der Aktzeptordichte
NA , und der Donatordichte ND ab. Für einen abrupten pn-Übergang ergibt sich:
kT
· ln
UD =
e
NA N D
n2i
= UT ln
NA ND
n2i
(1)
.
Hierbei ist k = 1,38·10−23 KJ die Boltzmann-Konstante, T die absolute Temperatur in Kelvin
und e = 1,6 · 10−19 C die Elementarladung, welche zusammen die Temperaturspannung
beschreiben. Das Maximum des internen elektrischen Feldes Ein liegt direkt am
UT = kT
e
pn-Übergang und beträgt:
Ein =
−eNA wp
−eND wn
=
.
(2)
Das gibt die Permittivität des verwendeten Halbleiters an. Die Ausdehnung der RLZ in
das n-dotierte bzw. p-dotierte Gebiet wird durch wn bzw. wp beschrieben. Die Weiten wn
und wp hängen wiederum von den gewählten Dotierungen und der äuÿeren Spannung UF
ab:
12
1
ND wn
2(UD − UF ) ND
·
wp =
·
=
e
NA NA + ND
NA
12
2(UD − UF ) NA
1
NA wp
wn =
·
·
=
e
ND N A + N D
ND
EL-V3 - 3
(3)
.
(4)
Die gegenüberliegenden RLZ-Enden lassen sich gut als Platten eines Kondensators auassen.
Der Abstand zwischen den Platten entspricht der gesamten Weite w der RLZ:
2(UD − UF ) NA + ND
w = wp + wn =
·
e
NA ND
12
.
(5)
Diese so genannte Sperrschichtkapazität CSP lässt sich dann über die Formel des Plattenkondensators mit der Querschnittsäche A des pn-Übergangs ausdrücken:
CSP
1
1
2eNA ND 2
A
· [4(UD − UF )]− 2 .
= =A·
w
NA + ND
(6)
Allgemein ist eine Kapazität C die durch eine Spannungsänderung dU hervorgerufene
Ladungsänderung dQ, sprich C = dQ
. Ändert sich die Spannung über dem pn-Übergang, so
dU
bedingt dies eine Änderung der injizierten Minoritätsladungsträger in das jeweilige Bahngebiet. Diese Ladungsänderung hervorgerufen durch die Spannungsänderung werden mittels
der Diusionskapazität CD berücksichtigt:
CD =
IF · τT
dQ
=
≈ gD · τT .
dUF
UT
(7)
Das τT gibt hier eine durchschnittliche Lebensdauer der überschüssigen Minoritätsträger an.
Der dierentielle Leitwert der Diode gD bestimmt sich wie folgt:
gD =
dIF
IF
≈
.
dUF
UT
(8)
Aus den bisherigen Überlegungen ergeben sich für eine pn-Diode ein Groÿsignal- (Bild 2(a))
und ein Kleinsignalersatzschaltbild (Bild 2(b)). Der Serienwiderstand RS berücksichtigt die
Bahnwiderstände im Halbleiter und die Kontaktwiderstände.
Bild 2: (a) Groÿsignal- und (b) Kleinsignalersatzschaltbild einer pn-Diode. Die in den Ersatzschaltbildern erhalteten Elemente sind der Serienwiderstand RS , der dierentielle Leitwert
gD , die Sperrschichtkapazität CSP und die Diusionskapazität CD .
2.2
I -U -Kennlinie
Im Folgenden Abschnitt wird auf den Ladungsträgertransport durch die pn-Diode mit
einer angelegten Spannung UF und die daraus resultierende I -U -Kennlinie eingegangen.
Für die folgende Betrachtung werden folgende Annahmen getroen: Die Spannung UF fällt
ausschlieÿlich über der RLZ ab (RS = 0); es ndet keine Rekombination und Generation
von Ladungsträger innerhalb der RLZ statt; die Störung ist klein.
EL-V3 - 4
Flussbereich
Für UF > 0 V verringert sich die innere Barriere um eUF im Vergleich zu UF = 0 V. Das
innere elektrische Feld verkleinert sich ebenfalls und führt dazu, dass Elektronen vom n- in
das p-Gebiet bzw. Löcher vom p- in das n-Gebiet injiziert werden. Die Minoritätsträgerdichte
im n- und p-Gebiet erhöht sich an den jeweiligen Ränder der RLZ, wodurch ein für den Ladungsträgertransport verantwortlicher Diusionsstrom hervorgerufen wird. Die Summe vom
Löcherdiusionsstrom Ip,Diff,max im n-Gebiet und dem Elektronendiusionsstrom In,Diff,max
im p-Gebiet am Rand der RLZ ergibt den gesamten durch die pn-Diode ieÿenden Strom
IF . Die Diusionsströme gehen mit gröÿer werdenden Abstand zum jeweiligen Rand der
RLZ in Feldströme Ip,Feld , In,Feld (auch Driftströme genannt) über. Es lässt sich zeigen, dass
für kleine Minoritätsträgerdichtestörungen das benötigte elektrische Feld für den Driftstrom
klein gegenüber dem maximalen elektrischen Feld innerhalb der RLZ ist. Wie im Bild 3(a)
zu sehen ist, addieren sich die Feld- und Diusionsströme am gleichen Ort zum gesamten
Strom IF . Für UF > 0 V leitet die Diode.
Sperrbereich
Beim anlegen einer Spannung UF < 0 V wird die innere Barriere sowie das innere elektrische
Feld erhöht. Die gröÿere Barriere verhindert das Elektronen vom n- in das p-Gebiert bzw.
Löcher vom p- in das n-Gebiet. Das gröÿere elektrische Feld führt dazu, dass die Elektronen
aus dem p- in das n-Gebiet und die Löcher vom n- in das p-Gebiet abgesaugt werden. Der
durch die Minoritätsträgerdichtestörung hervorgerufene Ladungträgertransport durch die
pn-Diode ist in diesem Fall deutlich kleiner verglichen mit UF > 0 V. Für UF < 0 V sperrt
die Diode.
Ideale Kennlinie
Die Kennlinie der idealen pn-Diode lässt sich durch die Shockley-Gleichung beschreiben:
UF
−1 .
IF = IS exp
nUT
(9)
Für die obige Gleichung gilt, dass im Bild 2(a) RS = 0 und somit U = UF ist. Das n steht
für den Idealitätsfaktor und nimmt Zahlenwerte zwischen 1 und 2 an. Für n ≈ 1 dominiert
der Diusionsstrom und bei n ≈ 2 bestimmt der Rekombinationsstrom den Verlauf der
Diodenkennlinie. Der Sättigungsstrom IS hängt vom Dotierungsprol des pn-Übergangs ab.
Bei einem abrupten pn-Übergang lässt sich IS unter Vernachlässigung von Generation und
Rekombination innerhalb der RLZ wie folgt ausdrücken:
Dn np0 Dp pn0
IS = e · A ·
+
Ln
Lp
.
(10)
IS hängt somit von der Diusionskonstante der Elektronen Dn und Löcher Dp , der Minoritätsträgerdichte der Elektronen np0 sowie der Löcher pn0 im thermodynamischen Gleichgewicht, der Diusionslänge der Elektronen Ln in das p-Gebiet und der Löcher Lp in das
n-Gebiet ab. Die ideale Diodenkennlinie für n = 1 und RS = 0 ist im Bild 3(b) aufgetragen.
In der Gleichung 9 ist der Spannungsabfall über den Bahngebieten im Halbleiter und
den Kontaktwiderständen nicht berücksichtigt (RS = 0). Ein RS > 0 lässt sich dadurch
berücksichtigen, dass man das UF aus der Gleichung 9 mit U − IF · RS ersetzt.
EL-V3 - 5
Bild 3: (a) Aufteilung der Diusions- und Feldströme am pn-Übergang
(b) Ideale I -U -Kennlinie einer pn-Diode (IS = 1 nA, UT = 26 mV).
Vergleich realer und idealer Kennlinie
Neben dem Serienwiderstand führen noch weitere Faktoren dazu, dass die gemessene reale
I -U -Kennlinie nicht mit der idealen I -U -Kennlinie einer pn-Diode übereinstimmen. Im Bild
4 werden die reale und ideale Kennlinie einer pn-Diode verglichen.
Im Flussbereich lassen sich bei der realen Kennlinie die Bereiche (a) bis (d) unterscheiden.
Im Bereich (a) bestimmen vor allem der Generations- und Rekombinationsstrom den Verlauf
der realen Kennlinie. Zum Teil lässt sich dies bei Gleichung 9 mit dem Idealitätsfaktor n ≈ 2
berücksichtigen. Eine gute Übereinstimmung zur Shockley-Gleichung mit dem Idealitätsfaktor n ≈ 1 besteht im Bereich (b). Darauf folgt der Hochinjektionsbereich (c), in dem
die Konzentration der injizierten Minoritäten vergleichbar zur Majoritätsträgerkonzentration ist. Die in Gleichung 9 vernachlässigten Feldströme müssen in diesem Arbeitsbereich
berücksichtigt werden. Der Serienwiderstand RS dominiert den Verlauf der Kennlinie im
Bereich (d).
Im Sperrbereich ieÿt ideal nur der Sättigungsstrom IS . In der Realität nähert sich
der Strom nicht dem konstanten Wert IS , sondern steigt betraglich mit gröÿer werdender
Sperrspannung USP = −UF an (Bereich (e) im Bild 4). Für den Anstieg sind nicht zu
vernachlässigende Generations- und Rekombinationsströme sowie Oberächeneekte verantwortlich.
Durchbruchsbereich
Im sogenannten Durchbruchsbereich ieÿt trotz einer angelegten Sperrspannung (UF < 0 V)
ein betraglich signikanter Strom |IF |. Bei ausreichend groÿen Sperrspannungen USP kommt
es bedingt durch das hohe elektrische Feld zu einem Durchbruch des pn-Übergangs und
der Strom |IF | steigt abrupt an. Der schnelle Anstieg von |IF | und die für den Durchbruch
erforderliche Spannung USP kann zum Überschreiten der maximalen Verlustleistung der
Diode kommen, wodurch sich der pn-Übergang zu stark erwärmt und endgültig zerstört
wird.
EL-V3 - 6
Bild 4: Vergleich der idealen und realen Diodenkennlinie, aus [Sze85a] Seite 91.
Das Durchbruchverhalten von Zener-Dioden (Z-Dioden) lässt sich für die Spannungsstabilisierung einsetzen. Die Z-Dioden weisen einen speziell gestalteten pn-Übergang auf,
so dass der Durchbruch bei einer bestimmten Sperrspannung UZ (auch Zenerspannung
genannt) auftritt. Für den Durchbruch sind zwei verschiedene Mechanismen verantwortlich:
der Zenereekt (Zener eect) und der Lawieneneekt (avalanche eect).
Beim Zenereekt tunneln Elektronen vom Valenzband des p-Halbleiters direkt in das
Leitungsband des n-Halbleiters. Hierfür muss der pn-Übergang sehr hoch dotiert sein, damit
das Valenz- und Leitungsband des jeweils gegenüber liegenden p- und n-Gebiet für eine
Erhöhung der Tunnelwahrscheinlichkeit hinreichend nah beieinander liegen. Der Zenereekt
dominiert bei Z-Dioden mit UZ / 6 V und weist einen negativen Temperaturkoezienten
auf.
Der Lawinendurchbruch bezeichnet den Prozess, in dem freie Elektronen durch das
elektrische Feld innerhalb der RLZ so stark beschleunigt werden, dass diese freien Elektronen
bei einem Zusammenstoÿ mit Gitteratomen weitere Elektronen aus den Atomrümpfen herauslösen. Die so zusätzlich gewonnenen freien Elektronen werden wiederum im elektrischen
Feld innerhalb der RLZ beschleunigt und generieren bei ihrer Kollision mit weiteren Gitteratomen weitere neue freie Ladungsträger. Der Name Lawinendurchbruch kommt daher, dass
sich die Anzahl der freien Elektronen lawinenartig selbst verstärkt, wie eine Lawine beim
herabrollen des Bergs immer gröÿer wird. Der Lawinendurchbruch bestimmt das Verhalten
von Z-Dioden mit UZ ' 6 V und weist im Gegensatz zum Zenereekt einen positiven
Temperaturkoezienten auf. Folglich ist nicht bei allen käuich zu erwerbenden Z-Dioden
der Zenereekt für das Durchbruchverhalten verantwortlich.
EL-V3 - 7
3 Grundlagen der Solarzelle
Die Solarzelle ist unter den regenerativen Energiequellen ein Energielieferant für den zukünftigen Energiemix. Genutzt wird hierbei die Sonneneinstrahlung bestehend aus elektromagnetischen Wellen vom Ultravioletten bis zum Infraroten Bereich, um diese mit Hilfe
des fotoelektrischen Eektes in elektrische Energie umzuwandeln. Der Wellenlängenbereich
dieses Sonnenlichtes reicht von 0.2 bis 3 µm. Mit EPH = hf bzw. EPH = hc/λ lässt sich jedem
Photon mit der Frequenz (f ) bzw. der Wellenlänge (λ) seine Energie (EPH ) zuordnen. Das
h = 6.63 · 10−34 JK in der obigen Gleichung bezeichnet das Plancksche Wirkungsquantum.
Bei einer mittleren Entfernung zwischen Sonne und Erde ist die Strahlungsintensität der
Sonne im freien Raum durch die Solarkonstante mit ca. 1353 W/m2 gegeben [Sze85b]. Durch
die Absorption und Reexionen innerhalb der Atmosphäre wird die Strahlung auf der Erdoberäche reduziert. Dieser Eekt wird durch den Air-Mass (AM) Quotienten berücksichtigt,
wobei für AM = 1.0 die Lichtstrahlen senkrecht auf die Erdoberäche auftreten und die
Strahlungsintensität auf ca. 925 W/m2 abgeschwächt ist [Sze85b]. Für kleinere Einfallswinkel
(wie z.B. im nördlichen Bereich) erhöht sich der AM Quotient und die Strahlungsintensität
nimmt weiter ab.
Die Solarzelle besteht z.B. aus Silizium mit einem achen pn-Übergang nahe der Oberäche, wie es in Bild 5(a) dargestellt ist. Die Vorderseite wird mittels eines ohmschen Kontaktes
in Form von Streifenleitungen mit Fingern und die Rückseite durch einen ganzächigen
ohmschen Kontakt kontaktiert. Eine Antireexionsschicht auf der vorderen Oberäche dient
der Erhöhung der Lichtabsorption. Wird nun die Solarzelle mit Licht bestrahlt, erzeugen
Photonen mit einer Energie kleiner als die Bandlücke des verwendeten Halbleiters keinen
Beitrag zum Spannungsausgang der Solarzelle. Nur Photonen mit einer Energie gröÿer
als die Bandlücke des Halbleiters erzeugen Ladungsträger in Form von Elektronen-LochPaaren. Durch das elektrische Feld innerhalb der RLZ werden die Ladungsträger voneinander getrennt, so dass zwischen der Vorder- und der Rückseite des Siliziumplättchen
eine Ausgangsspannung entsteht. Energien gröÿer als die Bandlücke werden als Wärme
an das Kristallgitter abgeben. Der gesamte Vorgang der Ladungsträgergeneration und der
Ladungstrennung ist in Bild 5(b) veranschaulicht.
Bild 5: (a) Vereinfachter Querschnitt durch eine Solarzelle aus Silizium.
(b) Banddiagramm des pn-Überganges einer Solarzelle von der Vorder- zur Rückseite.
Ein einfaches Ersatzschaltbild zeigt das Bild 6(b) und besteht aus einer Stromquelle IPH
parallel zur idealen Diode, einem Serienwiderstand RS und dem Lastwiderstand RL . Der
EL-V3 - 8
Fotostrom IPH beschreibt den durch die Photonen ideal hervorgerufenen Strom. IPH lässt
sich für eine vorgegebene Air-Mass (z.B. AM = 1) aus dem Produkt der Elementarladung
(e) und der Anzahl der Photonen mit einer Energie hf ≥ Eg im Sonnenspektrum bestimmen. Die ideale Diode dient der Modellierung des pn-Überganges. Der Serienwiderstand
RS berücksichtigt die Bahnwiderstände im Halbleiter und die Kontaktwiderstände an der
Vorder- und Rückseite der Solarzelle und soll zunächst mit RS = 0 als ideal angenommen
werden.
Bild 6: (a) Einfaches Ersatzschaltbild einer Solarzelle
(b) Ideale Kennlinie einer Solarzelle mit RS = 0. Für die Berechnung wurden folgende
Werte verwendet: IPH = 100 mA, IS = 1 nA, n = 1, UT = 26 mV.
Für die Diode lässt sich die ideale I − U -Kennlinie durch die bereits erwähnte ShockleyGleichung 9 beschreiben. Für den Fall RS = 0 gilt UF = U . Löst man nun die Knotengleichung für das Ersatzschaltbild erhält man die ideale I − U -Kennlinie für eine Solarzelle:
U
I = IS · exp
− 1 − IPH .
nUT
(11)
Die berechnete ideale Kennlinie ist im Bild 6(b) gezeichnet. Der Verlauf durch den vierten
Quadranten zeigt, dass hier Leistung entnommen werden kann. Normalerweise wird die
Kennlinie einer Solarzelle wie im Bild 7(a) gezeigt dargestellt. Dies kommt einer Spiegelung
der Kennlinie an der Abszisse im Bild 6(b) gleich. Der Schnittpunkt mit der Ordinate im
Bild 7(a) gibt den Kurzschlussstrom ISC an, der im Idealfall mit dem Strom IPH übereinstimmt. Die Leerlaufspannung UOC ergibt sich beim Schnittpunkt der Kennlinie mit der
Abszisse. Die Ausgangsleistung ist gegeben durch P = IU und erreicht einen maximalen
Wert bei PM = IM UM . Dies entspricht dem Betriebspunkt der maximalen Ausgangsleistung
(maximum power point). Der Wirkungsgrad η lässt sich aus dem Verhältnis der maximal
abgegebenen Leistung PM zur zugeführten Leistung PIN berechnen:
η=
PM
IM UM
F F · IPH UOC ∼
=
=
=
PIN
PIN
PIN
h
IPH · UOC − UT · ln 1 +
EL-V3 - 9
PIN
UM
UT
− UT
i
.
(12)
F F wird als Füll-Faktor bezeichnet und ist wie folgt deniert:
FF =
IM UM
.
IPH UOC
(13)
Die Eingangsleistung der Sonne PIN entspricht dem Integral über alle Photonen im
Sonnenspektrum. Der ideale Wirkungsgrad einer Siliziumsolarzelle beträgt bei 300 K ca.
28% [Neam03].
Bild 7: (a) Weitere Darstellung der idealen Kennlinie einer Solarzelle (RS = 0) mit Kennzeichnung
der maximalen Ausgangsleistung PM = IM UM .
(b) Verschlechterung der maximalen Ausgangsleistung PM = IM UM durch Kontaktwiderstände, hier simuliert mit RS = 4 Ω.
Der ideale Wirkungsgrad lässt sich aufgrund vielfältiger Einüsse bei einer realen Solarzelle nicht erreichen. Ein Hauptfaktor ist der durch die ohmschen Kontakte verursachte
Serienwiderstand RS . Bild 7(b) verdeutlicht, dass ein Serienwiderstand von 4 Ω die maximale Ausgangsleistung PM = IM UM deutlich verschlechtert. Der reale Serienwiderstand von
Solarzellen liegt je nach Ausführung zwischen 0.4 und 0.7 Ω. Ein weiterer Faktor ist die Ladungsträgerrekombination, die den Strom I verkleinert und die maximale Ausgangsleistung
um bis zu 25% reduzieren kann [Sze85b].
4 Messaufbau
Die Kennlinien der Dioden werden im Zwei-Punkt Messverfahren wie im Bild 8 dargestellt
aufgenommen. Die Dioden benden sich in einem Kasten mit sieben Anschlüssen. Zum
Aufnehmen der Kennlinien wird das Kabel (K2) mit der gewünschten Anschlussbuchse
verbunden. Das Kabel (K1) verbindet die Kathode der verschiedenen Dioden mit der SMU
und muss nicht umgesteckt werden. Die Kennlininen werden alle so aufgenommen, dass die
Spannung als Quelle herausgegeben und der hervorgerufene Strom gemessen wird.
Folgende Einstellungen sollten an der der SMU manuell vorgenommen werden:
1. Integrationszeit (integration time) auf Mittel (medium ≡ 4 ms) stellen.
EL-V3 - 10
2. Filter auf "Aus" (o) stellen.
Der Filter gibt die Anzahl der Messungen an, aus denen der arithmetische Mittelwert
für einen Messpunkt berechnet wird.
3. Supprimieren (suppress) ausschalten
Subtrahiert den beim Einschalten angezeigten Messwert von den nachfolgenden Messwerten.
Für die Beleuchtung des Solarmoduls steht eine Halogenlampe zur Verfügung. Die Intensität der Beleuchtung lässt sich mittels eines Transformators regeln.
Verwendete Geräte:
1. Source-Measurement-Unit (SMU) Keithley Model 236
Maximale Ausgangswerte: −100 mA < I < 100 mA, −110 V < V < 110 V
Beim Betrieb als Spannungsquelle bis 1.1 V beträgt die maximale Schrittweite 100 µV.
2. Transformator: DC Power Supply DF1730LCD
Achtung: Die Lampe darf nur im Bereich I < 1.7 A und V < 12.6 V betrieben werden!
Bild 8: Vereinfachte Darstellung des Versuchsaufbaus
EL-V3 - 11
5 Vorbereitungsfragen
Vorbereitungsaufgabe 5.1:
Allgemeine Fragen zum pn-Übergang:
1. Erklären Sie Anhand einer Skizze wie die Raumladungszone an einem pn-Übergang
entsteht.
2. Zeichnen Sie das Bänderdiagramm für einen pn-Übergang.
3. Zeichnen Sie das Schaltsymbol für eine Diode richtig herum in die obigen Skizzen aus
den Unterpunkten 1 und 2 ein.
Vorbereitungsaufgabe 5.2:
Fragen zur I -U -Kennlinie einer Diode:
1. Geben Sie die Shockley-Gleichung für die Beschreibung der I -U -Kennlinie einer Diode
an.
2. Skizzieren sie qualitativ die I -U -Kennlinie mit linear skalierter Abszisse und
a) linear
b) logarithmisch
skalierter Ordinate.
3. Wie lässt sich die Auswertung der Messaufgabe 6.1.2 realisieren?
4. Wie ändert sich die I -U -Kennlinie der Diode unter Berücksichtigung eines Widerstandes in Serie zum pn-Übergang? Wie lässt sich mit dieser Überlegung die Messaufgabe
6.1.3 umsetzen?
Vorbereitungsaufgabe 5.3:
Fragen zur Solarzelle:
1. Zeichnen Sie ein einfaches Ersatzschaltbild für eine Fotodiode unter Berücksichtung
von Bahn- und Kontaktwiderständen mit Hilfe eines Serienwiderstandes RS .
2. Schreiben Sie die Gleichung für die ideale I -U -Kennlinie einer Fotodiode für RS = 0
auf.
3. Skizzieren sie qualitativ die I -U -Kennlinie einer Fotodiode:
a) mit RS = 0 und im Dunkeln (ohne Beleuchtung).
b) mit RS = 0 und im Hellen (mit Beleuchtung).
c) mit RS > 0 und im Hellen (mit Beleuchtung).
4. Leiten Sie den Ausdruck für die maximale Leistung PM = IM UM der idealen Fotodiode
her. Hinweis : IPH IS .
EL-V3 - 12
6 Messaufgaben
Messaufgabe 6.1:
Nehmen Sie die I -U -Kennlinie der Diode D1 ohne Serienwiderstand und mit einem Serienwiderstand (R1 oder R2) auf.
1. Tragen Sie mit der Hilfe von Origin die I -U -Kennlinien der Diode D1 mit linearer
Achsenskalierung auf.
2. Extrahieren Sie aus der I -U -Kennlinie der Diode D1 ohne einen Serienwiderstand die
Gröÿen für den Sperrsättigungsstrom (IS ) und den Idealitätsfaktor (n). Erklären Sie
die Vorgehensweise.
3. Bestimmen Sie aus der I -U -Kennlinie der Diode D1 mit einem Serienwiderstand die
Gröÿe von RS auf zwei unterschiedliche Vorgehensweisen. Erklären Sie Ihr Vorgehen
und vergleichen Sie die ermittelten Werte von RS .
Messaufgabe 6.2:
Nehmen Sie die I -U -Kennlinie der Diode D2 auf.
1. Wo liegen die Unterschiede zwischen den Kennlinien von D1 und D2?
2. Um was für einen Diodentyp handelt es sich bei den jeweiligen Dioden?
Messaufgabe 6.3:
Nehmen Sie die I -U -Kennlinie des Solarmoduls auf:
a) im Dunkeln
b) mit künstlicher Beleuchtung.
1. Zeichnen Sie die gemessenen I -U -Kennlinien des Solarmoduls für beide Fälle mit
Origin ebenfalls mit linearer Achsenskalierung.
2. Bestimmen Sie für die Messaufgabe 6.3 b) die maximale Leistung PM und die zugehörigen Werte für IM und UM .
EL-V3 - 13
Literatur
[Neam03] D. A. Neamen: Semiconductor physics and devices: basic principles - third edition.
McGraw-Hill, New York, 2003.
[Reis05]
M. Reisch: Halbleiter-Bauelemente. Springer, Berlin, Heidelberg, 2005.
[Sze85a] S. Sze:
1985.
. John Wiley & Sons,
Physics of semicondunctor devices - second edition
[Sze85b] S. Sze: Semicondunctor devices, physics and technology. John Wiley & Sons, 1985.
[Thus05] F. Thuselt:
Physik der Halbleiterbauelemente: Einführendes Lehrbuch für Inge-
. Springer, Berlin, Heidelberg, 2005.
nieur und Physiker
EL-V3 - 14