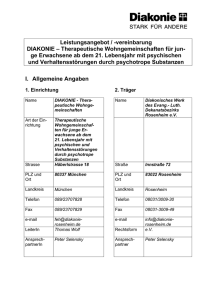
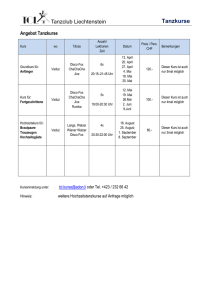
Gegenbeispiel

17 Grundbegriffe der Logik der Sprache PL
Erinnerung
Definition 11.1
Ein Satz A der Sprache AL ist genau dann logisch
wahr, wenn sich allein aus der Bedeutung der in ihm
vorkommenden logischen Ausdrücke ergibt, dass A
wahr ist bzgl. aller Bewertungen V von AL.
Definition 11.3
Ein Satz A der Sprache AL ist genau dann logisch
wahr (symb.: ! AL A), wenn sich allein aus den
Bedingungen der Definition 10.3 ergibt, dass A bzgl.
aller Bewertungen von AL wahr ist.
Grundbegriffe der Logik der Sprache PL
1
Definition 17.1a
Ein Satz A der Sprache PL ist genau dann logisch
wahr (symbol.: !PL A), wenn sich allein aus der
Bedeutung der in ihm vorkommenden logischen Ausdrücke ergibt, dass A wahr ist bzgl. aller Interpretationen I von PL.
Definition 17.1
Ein Satz A der Sprache PL ist genau dann logisch
wahr (symbol.: !PL A), wenn sich allein aus den
Bedingungen der Definition 16.11 ergibt, dass A
wahr ist bzgl. aller Interpretationen I von PL.
Grundbegriffe der Logik der Sprache PL
2
Definition 17.2
Sind A1, ..., An und A Sätze der Sprache PL, dann
folgt der Satz A genau dann logisch aus den Sätzen
A1, ..., An (symbol.: A1, ..., An !PL A), wenn sich allein
aus den Bedingungen der Definition 16.11 ergibt,
dass für alle Interpretationen I von PL gilt: Sind die
Sätze A1, ..., An alle wahr bzgl. I, dann ist auch A
wahr bzgl. I.
Grundbegriffe der Logik der Sprache PL
3
Frage
Wie kann man Sätze von PL auf ihre logische Wahrheit und Argumente von PL auf ihre Gültigkeit überprüfen?
Erstens
Es gibt leider kein Verfahren, das der Wahrheitstafelmethode entspricht, d.h. kein Verfahren, mit dem
man in einfacher Weise mechanisch für jeden Satz
der Sprache PL entscheiden kann, ob er logisch wahr
ist oder nicht.
Grundbegriffe der Logik der Sprache PL
4
Aber
Für einige Sätze und Argumente von PL kann man
zeigen, dass sie nicht logisch wahr bzw. gültig sind,
indem man Gegenbeispiele konstruiert.
Außerdem
Das Wahrheitsbaumverfahren lässt sich so erweitern,
dass man damit Sätze und Argumente von PL auf
logische Wahrheit bzw. Gültigkeit testen kann.
Grundbegriffe der Logik der Sprache PL
5
Die Gegenbeispielmethode
Ein Gegenbeispiel ist eine Interpretation I, bzgl.
deren der Satz A anerkanntermaßen falsch ist.
Merke
Wenn es ein solches Gegenbeispiel gibt, dann ist es
offensichtlich nicht der Fall, dass sich aus den Bedingungen der Definition 16.11 ergibt, dass es keine
Interpretation I geben kann, bzgl. deren der Satz A
falsch ist.
Die Gegenbeispielmethode
1
Beispiele
F1a → ∀xF1x
(1)
Hinweis
Ein Gegenbeispiel zu (1) ist eine Interpretation I,
bzgl. deren (1) anerkanntermaßen falsch ist.
Dies ist genau dann der Fall, wenn “F1a” bzgl. I wahr
und “∀xF1x” bzgl. I falsch ist.
Und dies ist wiederum genau dann der Fall, wenn V
“F1” auf eine echte, aber nichtleere Teilmenge von D
und “a” auf ein Element dieser Teilmenge abbildet.
Die Gegenbeispielmethode
(1)
F1a → ∀xF1x
(1′)
D = die Menge der natürlichen Zahlen
V(F1) = {x; x ist eine Primzahl}
V(a) = 7
(1″)
D = die Menge aller Tiere
V(F1) = {x; x ist ein Affe}
V(a) = Chita
(1″′)
D = {1, 2}
V(F1) = {1}
V(a) = 1
Die Gegenbeispielmethode
2
3
(2)
∀x(F1x → G1x) → ∀x(G1x → F1x)
Hinweis
Um ein Gegenbeispiel zu erhalten, muss V(F1) eine
echte Teilmenge von V(G1) sein.
(2′)
D = die Menge der ganzen Zahlen
V(G1) = {x; x ist eine natürliche Zahl}
V(F1) = {x; x ist eine Primzahl}
(2″)
D = die Menge aller Tiere
V(G1) = {x; x ist ein Tier}
V(F1) = {x; x ist ein Säugetier}
(2″′)
D = {1, 2}
V(G1) = {1, 2}
V(F1) = {1}
(2″″) D = {1}
V(G1) = {1}
V(F1) = ∅
Die Gegenbeispielmethode
(3)
4
∀x(F1x ∨ ¬F1x) → ∀xF1x ∨ ∀x¬F1x
Hinweis
Um ein Gegenbeispiel zu erhalten, darf V(F1) nicht mit
D identisch, aber auch nicht leer sein.
(3′)
D = die Menge der natürlichen Zahlen
V(F1) = {x; x ist eine Primzahl}
(3″)
D = die Menge aller Tiere
V(F1) = {x; x ist ein Säugetier}
(3″′)
D = {1, 2}
V(F1) = {1}
Die Gegenbeispielmethode
5
(4)
∀y∃xF2xy → ∃x∀yF2xy
(4′)
D = die Menge der natürlichen Zahlen
V(F2) = {<x, y>; x ist größer als y}
(4″)
D = die Menge aller Menschen
V(F2) = {<x, y>; x ist der Vater von y}
(4″′)
D = {1, 2}
V(F2) = {<1, 2>; <2 ,1>}
Die Gegenbeispielmethode
6
Ebenso wie zum Nachweis der Tatsache, dass ein Satz
A nicht logisch wahr ist, kann die Gegenbeispielmethode auch dazu verwendet werden zu zeigen, dass ein
Satz A nicht logisch aus den Sätzen A1, ..., An folgt.
In diesem Fall ist ein Gegenbeispiel allerdings eine
Interpretation I, bzgl. deren die Sätze A1, ..., An alle
anerkanntermaßen wahr sind, der Satz A dagegen
ebenso anerkanntermaßen falsch.
Die Gegenbeispielmethode
7
Beispiele
(5)∀x(H1x → G1x), ∀x(F1x → G1x)
!PL ∀x(F1x → H1x)
Hinweis
Um ein Gegenbeispiel zu erhalten, muss gelten:
• V(H1) ist eine Teilmenge von V(G1)
• V(F1) ist eine Teilmenge von V(G1)
• V(F1) ist keine Teilmenge von V(H1).
Die Gegenbeispielmethode
(5)
(5′)
8
∀x(H1x → G1x), ∀x(F1x → G1x)
!PL ∀x(F1x → H1x)
D = die Menge der natürlichen Zahlen
V(F1) = {x; x ist größer als 10}
V(G1) = {x; x ist größer als 5}
V(H1) = {x; x ist größer als 20}
(5″)
D = die Menge aller Tiere
V(F1) = {x; x ist ein Affe}
V(G1) = {x; x ist ein Säugetier}
V(H1) = {x; x ist eine Katze}
(5″′)
D = {1, 2}
V(F1) = {1, 2}
V(G1) = {1, 2}
V(H1) = {1}
Die Gegenbeispielmethode
9
(6)
∃x(G1x ∧ H1x), ∃x(F1x ∧ H1x)
!PL ∃x(G1x ∧ F1x)
Hinweis
Um ein Gegenbeispiel zu erhalten, muss gelten:
• Der Schnitt von V(G1) und V(H1) darf nicht leer sein
(V(G1) ∩ V(H1) ≠ ∅)
• Der Schnitt von V(F1) und V(H1) darf nicht leer sein
(V(F1) ∩ V(H1) ≠ ∅)
• Der Schnitt von V(G1) und V(F1) muss leer sein
(V(G1) ∩ V(F1) = ∅).
Die Gegenbeispielmethode
(6)
(6′)
10
∃x(G1x ∧ H1x), ∃x(F1x ∧ H1x)
!PL ∃x(G1x ∧ F1x)
D = die Menge der natürlichen Zahlen
V(F1) = {x; x ist größer als 20}
V(G1) = {x; x ist kleiner als 20}
V(H1) = {x; x ist größer als 10}
(6″)
D = die Menge aller Tiere
V(F1) = {x; x ist schwerer als 100 kg}
V(G1) = {x; x ist leichter als 100 kg}
V(H1) = {x; x ist ein Tier}
(6″′)
D = {1, 2}
V(F1) = {1}
V(G1) = {2}
V(H1) = {1, 2}
Die Gegenbeispielmethode
11